机载摄像机快速标定技术研究

张建花, 吕鹏涛, 邹　强

(中国飞行试验研究院 测试所， 西安　710089)



机载摄像机快速标定技术研究

张建花, 吕鹏涛, 邹强

(中国飞行试验研究院 测试所， 西安710089)

摘要：为了实现飞行试验中机载摄像机的快速标定，提出了一种基于光束法平差的高精度标定方法;该方法通过在被测试目标周围放置带有编码标志点的标定板，拍摄其多角度序列影像，经过相对定向、绝对定向、三维重建、捆绑调整，以及标志点之间的距离约束，得到数字摄像机内外方位元素和镜头畸变系数，实现机载摄像机快速标定;实验结果表明：该标定方法重投影误差小于1 cm，精度满足飞行试验测试要求，同时操作方便，适用于多场地试飞，具有鲜明的工程应用价值。

关键词:飞行试验；摄像机标定；光束法平差；编码标志

0引言

数字摄像机获取图像的直观性以及近景摄影测量的高精度等特点，在飞行试验中得到广泛应用。被测试目标越来越多的外部参数都采用摄影测量的手段获取。普通数字摄像机内外方位元素、镜头畸变等未知，不能进行测量计算，在进行精确测量之前必须进行标定。在机载环境下，由于摄像机安装位置受限制，控制场的布设和坐标测量实施困难。在无需做现场控制场的情况下，如何确定数字摄像机的内外方位元素和镜头畸变差是飞行试验中机载影像测量任务急需解决的问题。

1摄像机标定原理

1.1摄像机标定内容

摄像机标定的目的是确定从二维的影像信息得到三维空间信息之间关系的像机参数。这些参数分为两类，一类是相机的内方位元素，即主距f，像主点在像片中心坐标系里的坐标(x0,y0)以及镜头径向畸变参数(K1,K2)、偏心畸变参数(P1,P2)；另一类是相机的外方位元素，即摄影中心在选定坐标系下的3个坐标值(XS,YS,ZS)，以及代表影像空间姿态的3个元素(φ,ω,κ)。

1.2本文摄像机标定方法

1.2.1标定工具设计

摄像机标定过程需要大量的影像测量标志，为了使每一个点都具有唯一性，采用编码标志作为测量特征点，如图1所示。编码标志由内圆和外圆环两部分组成，其内圆是实心的圆，确定标志的中心位置；外圆环采用同心的环带，环带的长短和相互分布位置形成了编码。周围这种编码具有唯一性，并具有位置不变性和比例伸缩不变性。在平面面板上布设不同编号的编码标志和同一非编码标志作为标定工具，编码标志点之间的距离均已知。

图1　编码标志　　　　图2　标定工具

1.2.2标定过程

首先将标定板放置于机载摄像机前标准测量距离处，通过移动、旋转标定板获取其8个以上不同位置和姿态的图像；然后通过数字图像处理，识别出8组图像编码标志点的编码值和中心点图像坐标；利用摄影测量中相对定向原理计算出前两组图像的相对位置关系，并重建出编码标志点物方坐标；通过直接线性变换法重建出非编码标志点的物方坐标；最后通过光束法平差算法和标定板上任意两编码标志之间的长度约束条件，对摄像机内、外参数、物方特征点坐标等进行整体的迭代优化得到了摄像机标定参数，实现摄像机的标定。具体标定流程见图3。

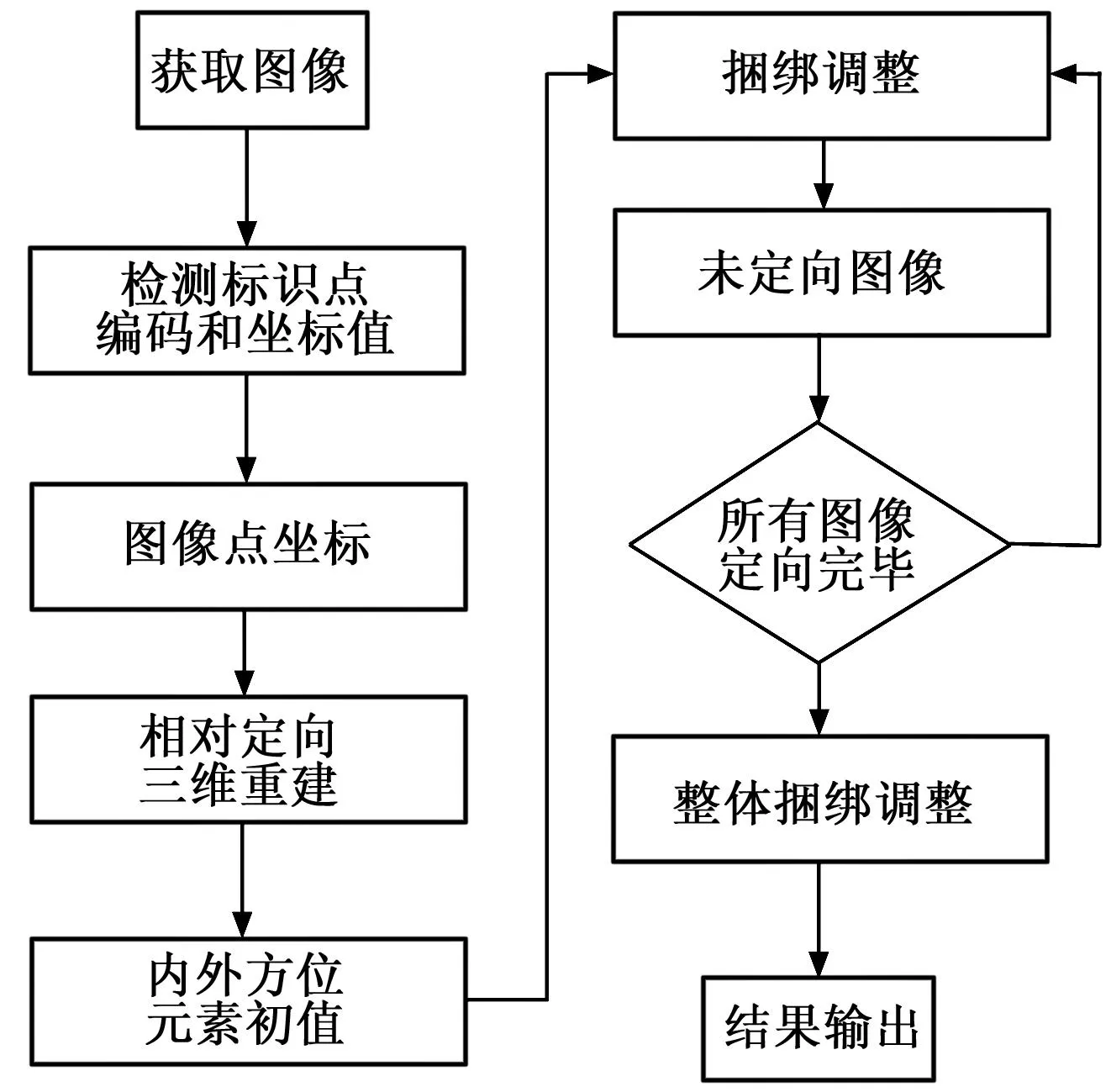
图3　摄像机标定流程图

1.3摄像机标定主要计算模型

1.3.1内外方位元素初值确定

根据立体视觉原理[1]：

(1)

其中：标志点的图像坐标(x,y) 对应的空间坐标为(X,Y,Z)，M为摄像机投影矩阵，(dx,dy)为CCD每毫米像素数。

对于某点(Xi,Yi,Zi)，令a34=1，可得除了a34外共有11个独立的未知量，至少需要6个标志点才能解算出投影矩阵。实际中，标定工具上有10个以上的控制点，可利用最小二乘法求解，可以得到除a34外投影矩阵M的其它元素。

摄像机投影矩阵M矩阵与摄像机内外参数的关系为：

(2)

其中：miT(i= 1,2,3)是求得的M矩阵的第i行的前3个元素组成的行向量，mi4(i=1,2,3)为M矩阵第i行的第四列元素，riT(i= 1,2,3)为旋转矩阵R的第i行向量，Xs,Ys,Zs为平移向量的3个分量。

由式(2)可得：

(3)

进而可以求解摄像机投影矩阵的元素a34，至此，求得M矩阵后，便可求解摄像机内外参数初始值。

1.3.2捆绑调整

捆绑调整[2]是对物体点和摄像机内外参数进行同时调整的过程，捆绑调整就是利用优化的方法使残差最小。捆绑调整的输入包括：物体点和图像点之间的关系方程；图像坐标作为观测值输入；物体点坐标和摄像机内外参数的初始估计值，这是需要优化的量，一般来说初始值能得到较快的收敛速度和收敛结果。

根据共线方程，并引入摄像机畸变，得到物体点和图像点之间的关系方程：

(4)

其中：

(5)

2编码标志的识别与检测

标志点位置的检测精度直接关系到标定结果最后的计算精度，因此提高参考点位置检测精度是摄影测量中非常关键的问题。编码特征点的自动识别过程如下：1)图像二值化；2)Canny算子进行边缘检测；3)圆形识别，得到圆心坐标；4)根据圆形与环形的比例关系，定位环形；5)根据环形的黑白颜色，进行01二进制编码；6)对01串编码进行位串循环，得到最小的编码数，即编码；7)将图像中的所有标志逐一识别，输出编码和对应的圆心坐标。具体如图4所示。

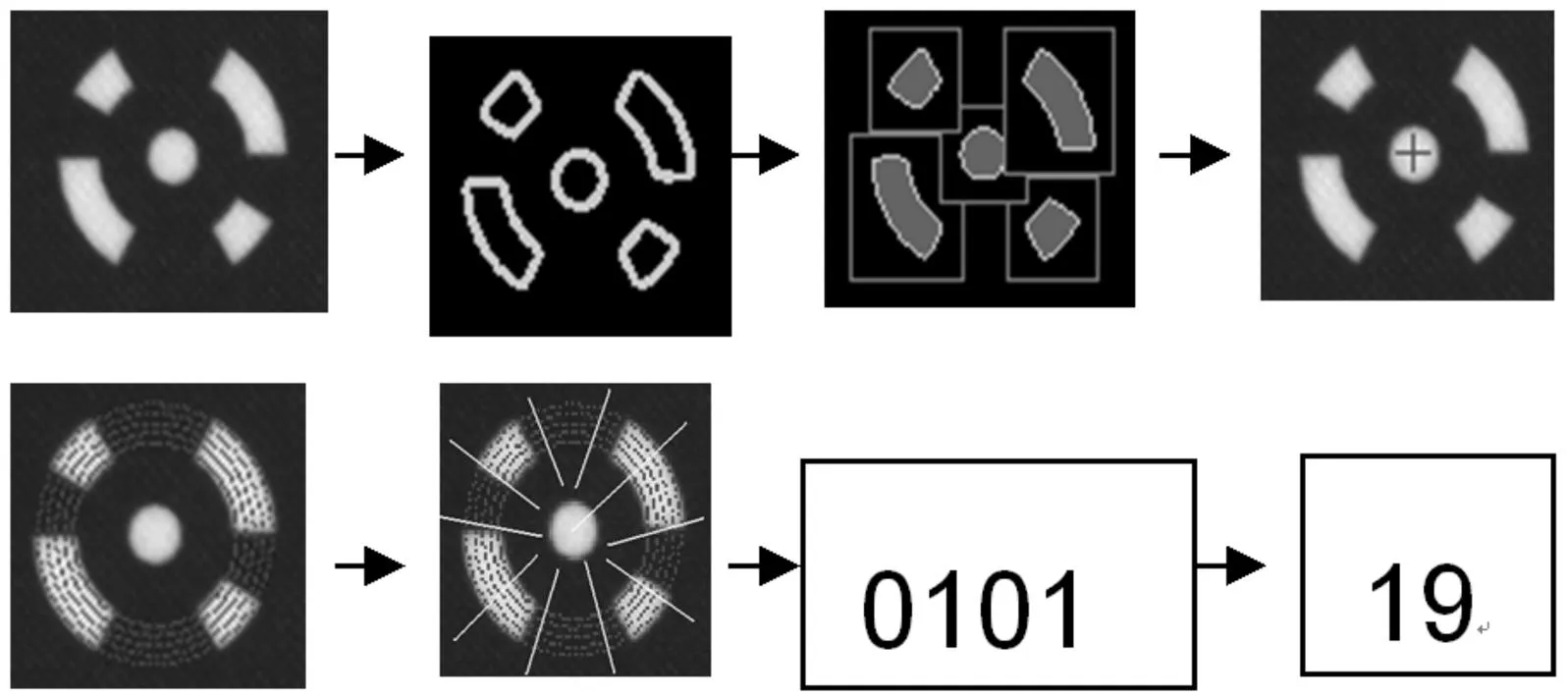
图4　编码标志的识别与检测

3标定实例与精度分析

3.1摄像机标定实验

某型飞机上所安装摄像机像幅为1 696×1 710。像素尺寸为12 μm×12 μm。相机焦距的标称值为f=12.5 mm。按照上述方法对其内外方位元素和及其畸变参数进行标定。结果如表1所示，其中内方位元素单位为像素，外方位直线元素单位为米，角元素单位为弧度。

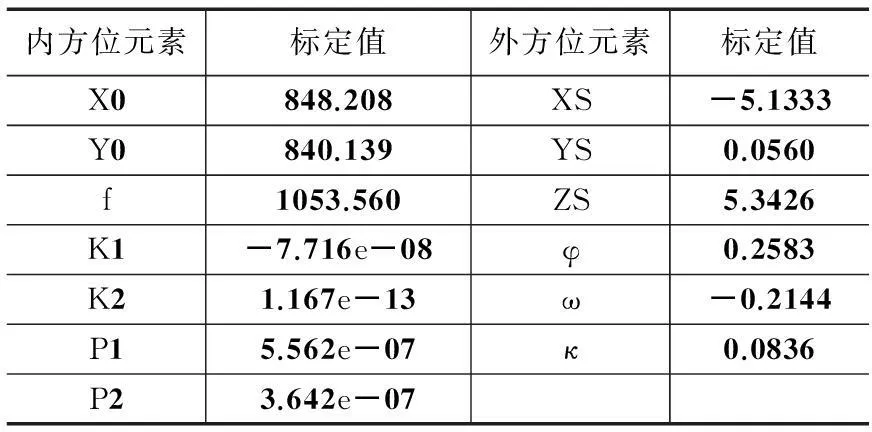
表1　标定结果

3.2精度分析

在摄像机视场内布设适量检查点，使用全站仪对检查点进行坐标测量。同时，采用单像机测量原理进行检查点二维坐标的解析计算，对两种方法所得结果进行比较，评估本文摄像机标定方法的精度。结果如表2所示。

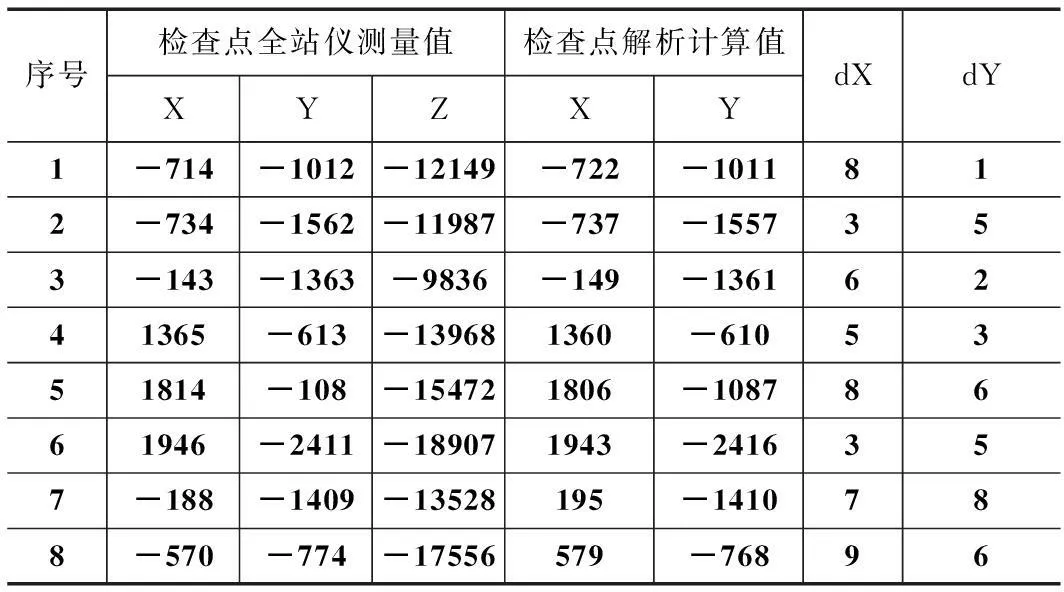
表2　坐标实测值与计算值比较 　mm

对表2数据进行分析，将Z方向当作定值，对X和Y方向的误差进行评估。X方向的最大误差是9 mm，Y方向的最大误差是8 mm，满足课题精度要求。

4结束语

本文主要研究了在无需做现场控制点的情况下，通过在被测试目标周围放置带有编码和非编码点的标定板，拍摄其不同角度的照片，经图像处理、相对定向、绝对定向、三维重建、捆绑调整等方法，实现在机载环境下摄像机内外方位元素和镜头畸变差参数准确快速地标定。相比传统的标定方法，本文标定方法简单，易于实施，在执行外场飞行任务时可以根据需要随时对摄像机像机进行标定，提高工作效率，克服了传统实验场标定方法的不足，具有鲜明的工程应用价值。

参考文献：

[1] 马颂德,张正友.计算机视觉-计算理论与算法基础[M].北京:科学出版社, 1997.

[2] 马扬飚,钟约先，戴小林.基于编码标志的数码相机三维测量与重构[J].光学技术, 2006, 32(6):865-868.

[3] 于宁锋. 数字摄影测量系统中非量测CCD相机标定算法[J].辽宁工程技术大学学报(自然科学版),2007,26(2):190-193.

[4] 郭君斌,郭晓松,杨必武,等.基于摄像机模型的平面动态测量方法[J].计算机测量与控制,2005,13(3):223-225.

[5] 张剑清,潘励,王树根.摄影测量学 [M ].武汉:武汉大学出版社,2003.

[6] 冯文灏. 近景摄影测量——物体外形与运动状态的摄影法测定[M]. 武汉: 武汉大学出版社, 2002.

[7] 胡浩，梁晋，唐正宗,等.大视场多像机视频测量系统的全局标定[J],光学精密工程,2012,20(2):369-378.

[8] Tang Z T，Liang J, Xiao Z Z, et al. Three-dimensional digital image correlation system for deformation measurement in experimental mechanics[J]. Optical Engineering，2010,49 (10): 103601.

[9] Xiao Z Z, Liang J, Yu D H, et al. An accurate stereo vision system using cross-shaped target self-calibration method based on photogrammetry[J]. Optics and Lasers in Engineering . 2010, 48 (12): 1252-1261.

Reseach of Airborne Camera Quickly Calibration Technology

Zhang Jianhua,Lv Pengtao,Zou Qiang

(Department of Test,China Flight Test Establishment,Xi’an710089,China)

Abstract:In order to achieve the quickly Calibration for airborne camera in flight test, an accurate calibration method based on bundle adjustment is presented. By place the calibration tool with coded and non-coded marks around the test target and take photographs from different angles. Then, the camera parameters which are included internal orientation elements, external orientation elements, lens distortion parameters and differential parameters can be quickly and accurately solved through relative orientation, absolute directional, 3D reconstruction, bundled adjustment and the distance constraint between two marks.The experiment results show that the proposed method in this paper can offer a considerable accuracy in a re-projection error less than 1cm which can satisfy the demands in flight test for precision. At the same time, it is easy to operate, suitable for more distinct sites flight test and with distinctive value for engineering application.

Keywords:flight test; camera calibration; bundle adjustment; coded mark

文章编号：1671-4598(2016)02-0166-02

DOI：10.16526/j.cnki.11-4762/tp.2016.02.045

中图分类号：TP391

文献标识码：A

作者简介：张建花(1983-)，女，陕西商洛人，硕士研究生，主要从事机载影像测量方向的研究。

收稿日期：2015-07-15；修回日期：2015-11-16。