基于Top-hat变换的OSAHS图像边缘检测算法

王英立，刘丽影，李思思

(哈尔滨理工大学，哈尔滨　150080)



基于Top-hat变换的OSAHS图像边缘检测算法

王英立，刘丽影，李思思

(哈尔滨理工大学，哈尔滨150080)

摘要：提出了一种基于多方向、多尺度Top-hat变换的图像边缘检测方法，应用于阻塞性睡眠呼吸暂停低通气综合症(Obstructive Sleep Apnea Hypopnea Syndrome, OSAHS)早期病理图像的边缘检测及诊断；通过对OSAHS早期病理图像的观察分析，针对待处理图像形状各异，并且含有噪声的特点，构造了不同方向、不同尺度的Top-hat算子增强图像的对比度，利用形态学梯度进行边缘检测，然后把各个算子检测到的图像边缘按照一定的权重进行组合，得到理想的边缘，以便准确地获得病理图像的相关参数，进而实现医学电子诊断；对OSAHS早期病理图像：口腔图像、咽喉声带处图像、鼻道内部图像处理、分析的结果表明，与传统的边缘算子相比较，该方法能使图像的边缘信息更完整、更准确，图像的边缘闭合度可达到97.67%，为实现医学电子诊断打下坚实的基础。

关键词：数学形态学；结构元素；Top-hat算子; 边缘检测

0引言

阻塞性睡眠呼吸暂停低通气综合症(obstructive sleep apnea hypopnea syndrome，OSAHS)是一种患病率较高的口腔疾病，严重影响着人们的睡眠质量和身体健康。目前，医生主要是利用电子喉镜仪来观测口腔，通过肉眼观察进行诊断，这样不但会造成诊断量的增加，也会使误诊率大幅上升。只要将图像处理软件应用到电子喉镜仪中，就可以利用数学形态学对图像进行处理，准确地提取出感兴趣区域的边缘，进而算出相关医学参数，实现电子诊断。

边缘是指图像周围像素灰度急剧变化的部分，是图像最基本的特征[1]。边缘检测在整个图像处理的过程中起着至关重要的作用，直接影响着图像后续处理的结果和精度[2-3]。常见的边缘检测算子都可以有针对性地对图像进行边缘检测，但是都具有一定的局限性。Roberts算子适用于处理具有陡峭的低噪声的图像，但是该算子对边缘的定位不准确，易丢失部分边缘； Prewitt算子适用于处理边缘灰度值尖锐的图像，但是该算子滤除噪声能力较差，会影响到边缘检测的质量；Log算子对噪声有一定的抑制作用，但同时也抑制了原有的边缘信息，所以在进行边缘检测时无法达到理想的效果； Canny算子不容易受噪声干扰，能将噪声较好地滤除，但同时也容易平滑掉一些边缘信息，导致边缘线条不清晰。

针对传统边缘算子存在的问题，本文应用了基于数学形态学的多方向、多尺度Top-hat算子对OSAHS图像进行处理，利用不同尺度、不同方向圆形、线形结构元素构造出的Top-hat算子增强图像对比度，利用形态学梯度进行边缘检测，得到具有良好闭合度的图像边缘，准确地计算出相关医学参数。与传统的边缘算子相比较，该方法能更完整的保持图像细节，使图像的边缘信息更准确，图像的边缘闭合度可达到97.67%。

1算法原理与实现

1.1灰度形态学的基本算法

灰度膨胀和灰度腐蚀是灰度形态学中两种基础算法[4-5]。设A(x,y)是输入图像，B(x,y)是结构元素。如果用Z表示实整数的集合，同时假设(x,y)是来自Z×Z的整数，A和B是对应坐标为(x,y)像素灰度值的函数。则B(x,y)对A(x,y)进行灰度膨胀和灰度腐蚀分别表示为：

(1)

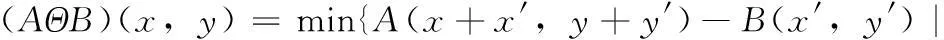
(2)

其中：DA、DB分别是A(x,y)、B(x,y)的定义域。

开运算和闭运算分别是由膨胀和腐蚀的不同组合而形成的。开运算就是先进行腐蚀运算，后进行膨胀运算，记为A°B。相对应地，闭运算就是先进行膨胀运算，后进行腐蚀运算，记为A·B。它们分别表示为：

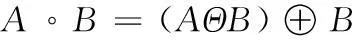
(3)

(4)

1.2结构元素的选取

本文的输入图像为OSAHS早期病理图像，包括口腔图像、鼻腔图像、咽喉声带处图像等。由获取的图像可以看出，待处理图像形状各异，并且都含有噪声。若采用单一的结构元素对图像进行边缘检测，抑制噪声的同时，也会滤除部分边缘信息，降低感兴趣区域的边缘闭合度，为后续计算相关医学参数带来困难。

图1为分别选取3×3、5×5、7×7、9×9圆形结构元素对图像进行边缘检测结果的量化比较图。从图中可以看出，在同一噪声强度下，随着结构元素尺度的增大，检测出图像边缘的闭合度却大幅减小。在相同结构元素的条件下，噪声强度的增大，也会导致检测出图像边缘的闭合度减小。由此可见，在边缘检测的过程中，要获得很好的闭合度，结构元素的选取尤为重要，既要检测出边缘信息，也要很好地滤除噪声。

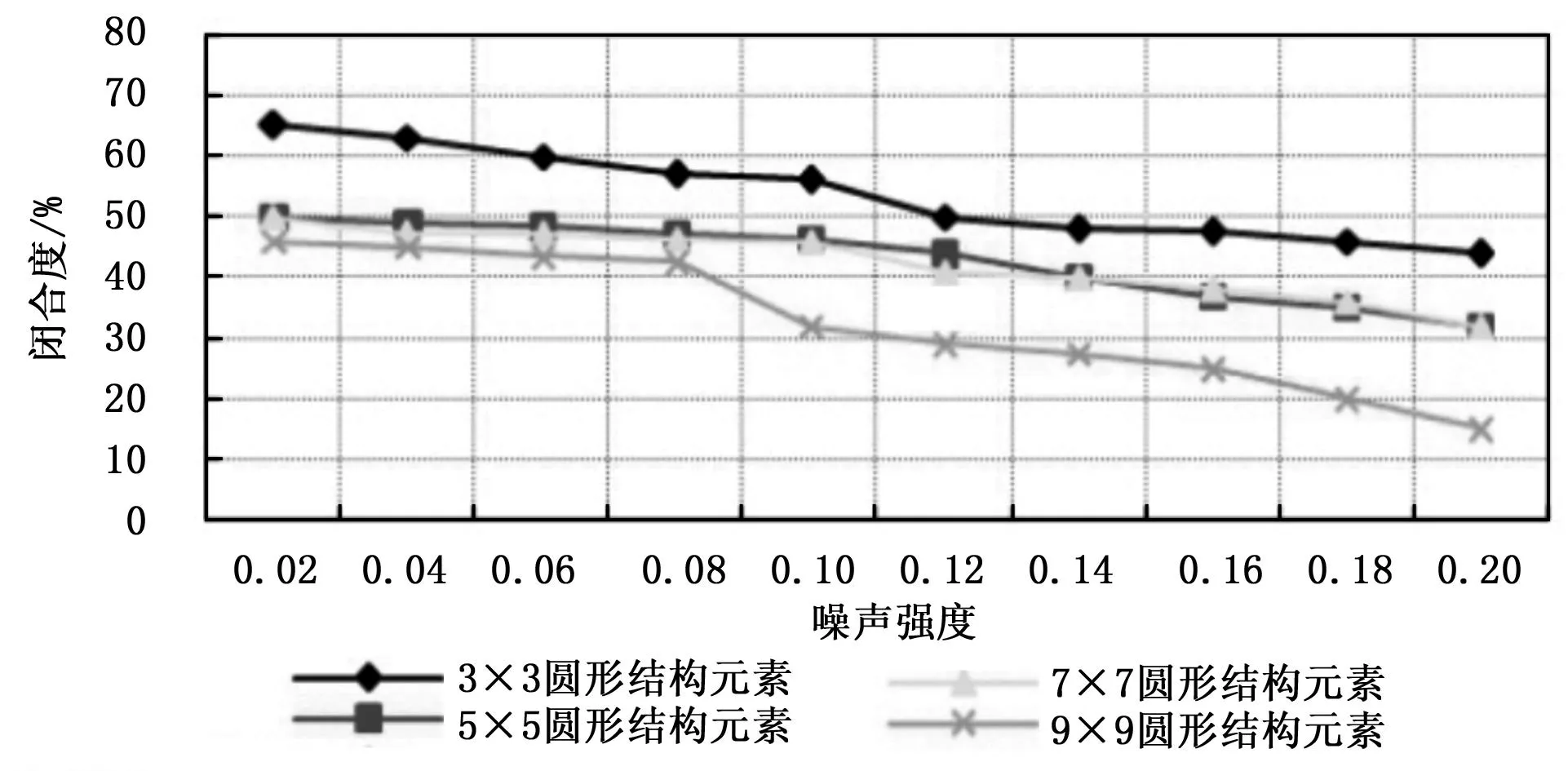
图1　单尺度Top-hat算子边缘检测结果量化比较图

虽然大尺度结构元素去除噪声的能力更强，却丢失了较多的边缘信息；小尺度结构元素能检测出更细致的边缘信息，却没有足够大的去除噪声的能力。因此，只有综合利用不同尺度算子的特性，才能更有效地去除噪声、更准确地检测出图像的边缘信息[6-10]。

利用形态学膨胀运算可以获得不同尺度的结构元素。即大尺度结构元素可通过对小尺度结构元素进行膨胀运算得到[11]。假设Bm为有限结构元素，则多尺度结构元素可表示为：

(5)

其中：m为尺度参数，取正整数。如设B1为最小的3×3圆形结构元素，那么B2和B3将分别为5×5和7×7的圆形结构元素，可推知Bm为(2m+1)×(2m+1)的圆形结构元素。结构元素B1、B2、B3如图2所示。

图2　多尺度结构元素

采用简单对称的圆形结构元素对图像进行边缘检测时，减弱了对不同方向边缘的敏感性，导致检测出的边缘方向细节不完整，存在断裂现象[12-13]。为了提高算法对不同方向边缘信息的敏感性，检测出完整、准确的边缘。本文构造了4个方向的结构元素bn，n为尺度参数，取正整数。其中结构元素b1如图3所示。

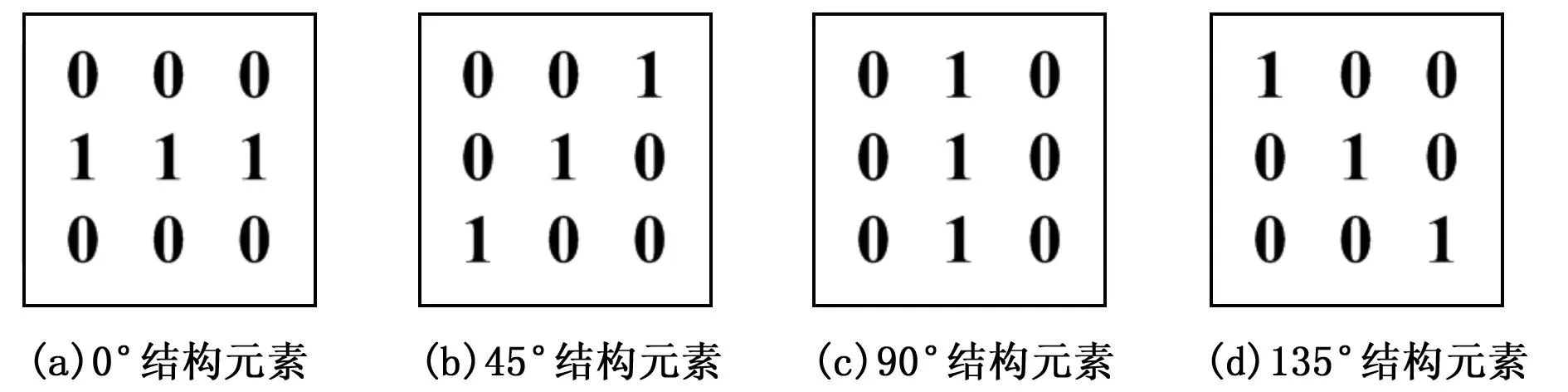
图3　多方向结构元素

1.3Top-hat算子的改进

Top-hat算子根据使用开、闭运算的不同而分为开Top-hat(Opening Top Hat)算子和闭Top-hat(Closing Top Hat)算子，分别表示为：

(6)

(7)

Top-hat算子具有高通滤波的某些特性。而图像的边缘就是图像的高频部分，边缘检测即是要检测出图像的高频分量[14]。因此，Top-hat算子在进行图像边缘检测的过程中更具优势，它可以有效地识别出各种背景下的目标，提取出合理、准确的目标边缘[15]。

对于含有噪声的OSAHS图像，传统的形态学Top-hat算子采用相同的结构元素进行开启、闭合运算，对噪声的抑制并不理想，同时也会导致边缘信息缺失。本文提出多方向、多尺度的结构元素构成的综合型Top-hat算子如下：

(8)

(9)

其中：Bi、bk代表小尺度结构元素，Bj、bl代表大尺度结构元素。[i,j]、[k,l]分别是尺度参数m、n的取值范围。小尺度结构元素精准地刻画出边缘细节、大尺度结构元素滤除噪声、多方向的结构元素提高算法对不同方向边缘的敏感性，改善边缘断裂现象。

1.4边缘检测

Step1：利用Top-hat算子增强图像对比度，增强后的图像为：

Sm(x,y)=OTHB(x,y)+A(x,y)-CTHB(x,y)

(10)

Sn(x,y)=OTHb(x,y)+A(x,y)-CTHb(x,y)

(11)

Step2：利用多尺度、多方向形态学梯度算子进行边缘检测，检测到的边缘图像为：

(12)

(13)

Step3：把各个算子检测到的边缘按照一定的权重进行组合，得到理想的图像边缘为：

(14)

其中：ωm是不同尺度结构元素的权值，ωn不同方向结构元素的权值。本文取ωn=1/n，即不同尺度的4方向结构元素bn所占比重相同。不同尺度结构元素的权值ωm的计算方法如下：

Step1：利用多尺度的结构元素Bm对图像进行闭开、开闭运算，进而求得不同尺度结构元素闭开、开闭运算后的均值图像Fm(x,y)如下：

(15)

Step2：计算不同尺度下的标准差值：

(16)

Step3：根据不同尺度下标准差值的比例确定权值：

(17)

其中：Δj-m为第j-m个结构元素的标准差值。

2实验结果

本文选取了三组典型的OSAHS图像进行处理，如图4~图6所示，主要是3种引发口腔疾病的发病源处，图4为健康口腔图像；图5为慢性咽炎，需要进行药物治疗患者的咽喉声带处图像；图6为脉样体增生、肥大，需要进行手术治疗患者的鼻道内部图像。

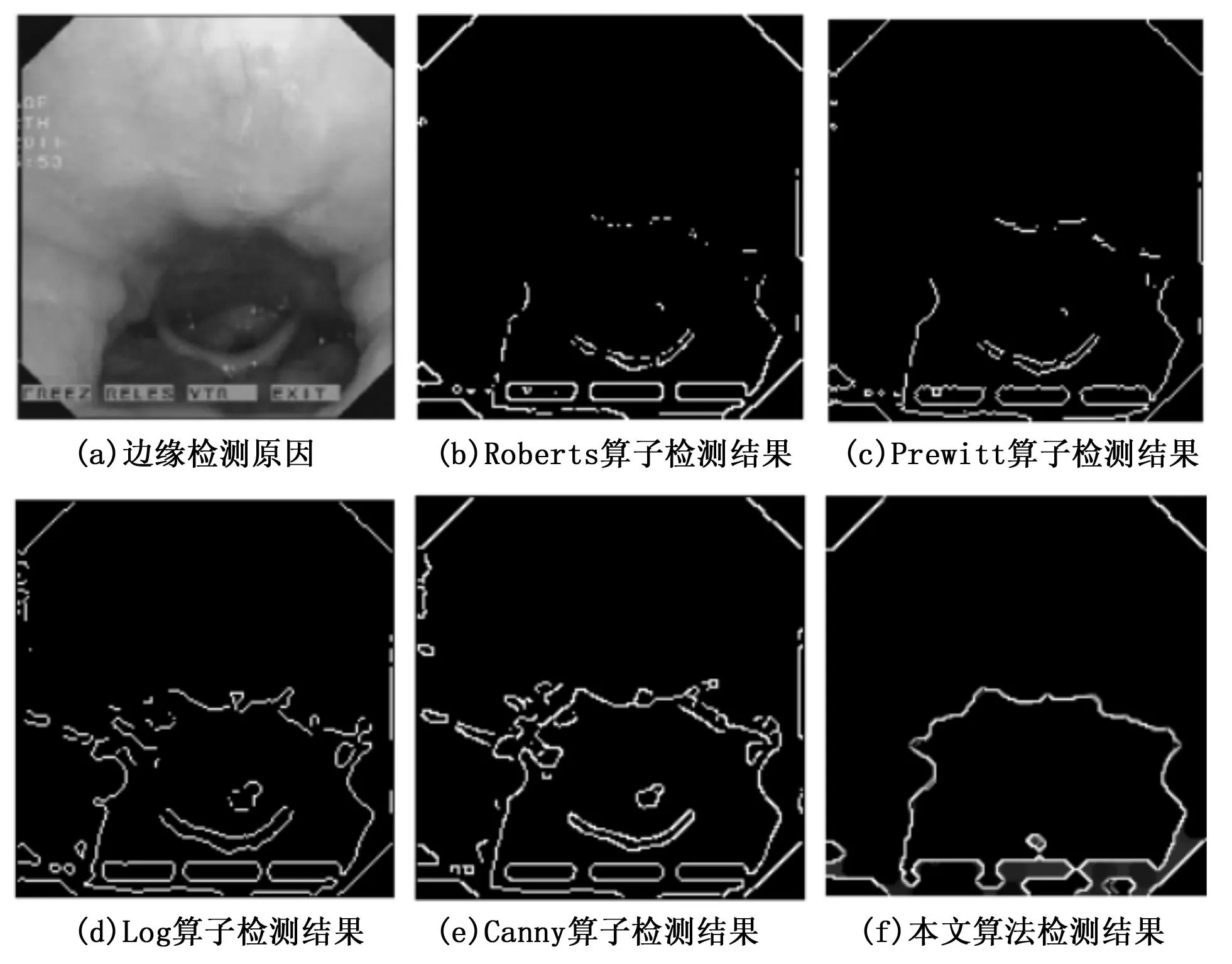
图4　口腔图像实验结果对比图

图4列出了Roberts算子、Prewitt算子、Log算子、Canny算子和本文提出的Top-hat算子对口腔图像进行边缘检测的结果。图4(a)为边缘检测原图像，4(b)为Roberts算子边缘检测的结果，图4(c)为Prewitt算子边缘检测的结果，图4(d)为Log算子边缘检测的结果、图4(e)为Canny算子边缘检测的结果，图4(f)为本文算法边缘检测的结果。从图中可以看到Roberts算子丢失了部分边缘；Prewitt算子对灰度值变化较大部分的边缘检测效果较好，但是也丢失了部分边缘；Log算子对噪声比较敏感，出现了较多的伪边缘信息；Canny算子检测出的边缘虽然比较完整，但是同样出现了较多的伪边缘信息；本文提出的算法可以准确地检测出图像的边缘信息，并且具有很好的闭合度。

图5列出了Roberts算子、Prewitt算子、Log算子、Canny算子和本文提出的Top-hat算子对咽喉声带处图像进行边缘检测的结果。图5(a)为边缘检测原图像，5(b)为Roberts算子边缘检测的结果，图5(c)为Prewitt算子边缘检测的结果，图5(d) 为Log算子边缘检测的结果、图5(e)为Canny算子边缘检测的结果，图5(f)为本文算法边缘检测的结果。从图中可以看到Roberts算子和Prewitt算子检测出的边缘比较完整，但出现了较多的伪边缘信息；Log算子检测出的边缘存在断裂现象，闭合度较差；Canny算子检测的边缘虽然比较完整，但是同样出现了较多的伪边缘信息；本文提出的算法可以较为准确地检测出图像的边缘信息，并且具有很好的闭合度。

图5　咽喉声带处图像实验结果对比图

图6　鼻道内部图像实验结果对比图

图6列出了Roberts算子、Prewitt算子、Log算子、Canny算子和本文提出的Top-hat算子对鼻道内部图像进行边缘检测的结果。图6(a)为边缘检测原图像，6(b)为Roberts算子边缘检测的结果，图6(c)为Prewitt算子边缘检测的结果，图6d) 为Log算子边缘检测的结果、图6(e)为Canny算子边缘检测的结果，图6(f)为本文算法边缘检测的结果。从图中可以看到Roberts算子、Prewitt算子、Log算子、Canny算子检测出的边缘都比较完整，但是都存在边缘断裂现象，闭合度较差，并且存在较多的伪边缘信息；本文提出的算法可以较为准确地检测出图像的边缘信息，并且具有较好的闭合度。

表1列出了几种算法边缘闭合度的性能比较，表中数值为3组图像相应数值的均值。从表1可以看出，利用本文算法进行边缘检测得到图像的边缘的闭合度远远好于其他算子检测到的图像边缘。

表1　几种算法的性能比较

3结束语

本文利用综合型Top-hat算子实现了对OSAHS图像边缘的精确检测。对OSAHS图像进行预处理后，利用构造的多方向、多尺度Top-hat算子增强图像对比度，利用形态学梯度进行边缘检测，然后把各个算子检测到的边缘按照一定的权重进行组合，进而得到理想的图像边缘。与传统的边缘算子相比较，该方法能完整、准确的保留图像细节，图像的边缘闭合度可达到97.67%，为后期精准地计算OSAHS图像的相关医学参数，实现医学电子诊断打下坚实的基础，具有很好的实用性。

参考文献：

[1] 丁文，李勃，陈启美. Canny色彩边缘检测及分类新方法[J]. 北京邮电大学学报, 2012, 35(1): 115-119.

[2] 李伟斌，高二，宋松和. 一种全局最小化的图像分割方法[J]. 电子与信息学报，2013, 35(4): 791-796.

[3] 吴一全，宋昱，周怀春. 基于各向异性数学形态学的火焰图像边缘检测[J]. 仪器仪表学报，2013,34(8): 1818-1825.

[4] 余永维，殷国富，蒋红海，等. 磁瓦表面图像的自适应形态学滤波缺陷提取方法[J]. 计算机辅助设计与图形学学报, 2012, 24(3): 351-356.

[5] 郑强，董恩清. 一种新的基于二值水平集和形态学的局部分割方法[J]. 电子与信息学报, 2012, 34(2): 375-381.

[6] 李文博，罗代升. 基于Curvelet和Wavelet结合的SAR图像降噪方法[J]. 四川大学学报: 工程科学版, 2012, 44(1): 145-149.

[7] 尹平，王润生. 自适应多尺度边缘检测[J]. 软件学报, 2000, 11(8)：990-994.

[8] 刘帅奇，胡绍海，肖扬，等. 基于局部混合滤波的 SAR 图像边缘检测[J]. 电子与信息学报, 2013, 35(5): 1120-1127.

[9] 罗玲，解梅，陈杉. 基于多尺度形态滤波的分水岭图像分割方法[J]. 计算机辅助设计与图形学学报，2004, 16(2):168-173.

[10] Pellegrino F A, VanZella W，Torre V. Edge detection revisited [J]. IEEE Transactions on Systems, Man and Cybemetics-PartB: Cybernetics, 2004, 34(3): 1500-1518.

[11] 刘艳莉，桂志国. 基于形态学的可变权值匹配自适应图像增强算法[J]. 电子与信息学报，2014, 36(6): 1285-1291.

[12] 师文，朱学芳，朱光. 基于形态学的MRI图像自适应边缘检测算法[J]. 仪器仪表学报, 2013, 34(2):408-415.

[13] 郑绍华，陈健，潘林，等. 基于形态学的可变权值匹配自适应图像增强算法[J]. 电子与信息学报, 2014, 36(11): 2586-2592.

[14] 张立国，杨瑾，李晶，等. 基于小波包和数学形态学结合的图像特征提取方法[J]. 仪器仪表学报，2010, 31(10): 2285-2290.

[15] 曾明，李建勋. 基于自适应形态学Top-hat滤波器的红外弱小目标检测方法[J]. 上海交通大学学报，2006, 40(1): 90-97.

OSAHS Image Edge Detection Algorithm Based on Top-hat Operator

Wang Yingli, Liu Liying, Li Sisi

(Harbin University of Science and Technology, Harbin150080,China)

Abstract:Proposes an image edge detection method based on multi-directional, multi-scale Top-hat operators, and apply the method to the edge detection and diagnosis of OSAHS (Obstructive Sleep Apnea Hypopnea Syndrome, OSAHS) early pathological images. Through the observation and analysis of the OSAHS early pathological images, considering the image Shapesand noise,construct multi-directional, multi-scale Top-hat operators, and they are used to enhance the contrast of images. Use morphological gradient to detect the edge. Then the ideal image edge is obtained by combining the edges of the image detected by each operator according to a certain weight, so that I can obtain relevant parameters of pathology images accurately, and then achieve electronic medical diagnosis. The processing results of OSAHS early pathological images including oral image, vocal cords oral image and inside nose image show that the operator proposed in this paper can make the edge information of the image more complete and accurate, compared with conventional edge operator, and edge closure of image is 97.67%, in the future can provide a solid foundation for electronic medical diagnosis.

Keywords:mathematical morphology; structural elements; top-hat operator; edge detection

文章编号：1671-4598(2016)02-0133-04

DOI：10.16526/j.cnki.11-4762/tp.2016.02.036

中图分类号：TP391.9

文献标识码：A

作者简介：王英立(1973-)，男，黑龙江哈尔滨人，博士，副教授，硕士研究生导师，主要从事图像处理技术、光电测试技术与仪器、信号检测及信息处理技术方向的研究。

基金项目：黑龙江省教育厅科学技术研究项目(12541165)。

收稿日期：2015-11-13；修回日期：2015-12-07。