基于PSO-DE算法的污水处理优化控制研究
叶永伟, 葛沈浩, 任设东, 钱志勤
(浙江工业大学 特种装备制造与先进加工技术教育部 浙江省重点实验室, 杭州 310014 )
基于PSO-DE算法的污水处理优化控制研究
叶永伟, 葛沈浩, 任设东, 钱志勤
(浙江工业大学 特种装备制造与先进加工技术教育部 浙江省重点实验室, 杭州310014 )
摘要:针对目前污水处理系统能耗过大,处理效果差等问题,提出了基于改进型粒子群算法的优化控制;采用粒子群差分进化算法(PSO-DE)可以提高粒子全局搜索能力与收敛速度,克服粒子早熟现象;在实际应用中建立以溶解氧浓度(DO)与污泥排放量(Qw)为变量,以能耗与出水水质为约束条件的数学模型,通过算法全局寻优求解,验证结果表明该算法能保证出水水质前提下降低污水处理能耗。
关键词:污水处理;优化控制;改进粒子群算法
0引言
随着现在工业生产与城市化进程加快,环境污染日益加重,其中水污染问题给社会生产与人们生活带来很大影响。如何有效,快速,经济,合理地解决污水问题引起了社会关注。造成目前污水处理能耗过大,处理效果不理想的原因主要有:1)涉及到多变量的生化处理过程;2)系统中的变量不仅包括物理单位,生物单位,还有化学单位;3)出水水质参数仪器仪表无法实时检测,数据处理需要一定时间,导致出水水质难以保证;4)处理工艺中药剂的使用费用以及大功率设备运行费用高等难题。为了尽可能在保证水质的前期下降低运行费用,优化控制成为国内外学者研究重点。污水处理中电能约占能耗90%[1]。例如污水处理曝气系统中电机功率较大,动力消耗约占总电量消耗的40%~50%,普遍采用的传统PID控制效果差,通过仿人智能PID的使用能减少能耗10%~20%,但该算法只能解决单局部优化。叶洪涛等人[2]采取免疫算法对污水处理运行费用优化控制取得一定效果。郑光勇等人[3]建立基于粒子群的污水水质预测模型。采用遗传算法研究污水运行费用最优控制,都只能在局部有明显效果,泛化能力差。粒子群算法(PSO)作为一种群体智能算法,具有操作简单,自适应控制,全局搜索等特点,广泛应用于系统的优化控制,并且在污水处理中的优化研究也取得一定效果。但算法存在的问题前期有较快的收敛速度,进化代数增加后期收敛速度变慢[4],这样对于复杂的多维度的污水处理控制系统而言用基础的PSO就无法满足应用。差分进化算(DE)在初期收敛速度较慢,但随着进化代收的增加,收敛速度相比粒子群算法有了明显的加快。通过结合各自算法的优点,设计出一种基于粒子群与差分进化算法的交替混合算法。在前期利用PSO自身的快速收敛优势,到了后期结合DE的收敛优势,从而避免了PSO容易早熟缺点,提高算法全局的寻优能力。
1污水处理数学模型
1.1污水处理工艺路线
对一般的城市污水处理主要分为三级,第一级的处理主要包括污水提取,粗细格栅过滤,曝气沉淀;第二级处理根据实际情况来选择合适的工艺主要包括生化处理,二次沉淀,污泥处理;第三级处理包括絮凝沉淀,杀菌消毒等流程。具体工艺分布如图1所示。

图1 污水处理工艺路线示意图
根据对污水处理实际生产与应用中分析得出,在工程规模一定的情况下,从装机容量,技术成熟性,主要参数性能达标能力分析。采用了比较主流的AA/O工艺路线,该工艺特色是典型的除磷脱氮工艺,关键在于生化池由厌氧(ANAEROBIC)、缺氧(ANOXIC)耗氧(OXIC)三部分组成,通过在回流与进水分配上合理的控制能更好的脱氮除磷,适合城市生活污水含氮含磷比例较高下使用。
1.2污水处理状态方程
主要对污水处理中其关键作用的生化池进行建模,活性污泥法系统如图2所示。通过简单假设曝气池主要可以分为微生物和有机物底物,忽略进水中的微生物浓度,二沉池中没有生物代谢[6]。
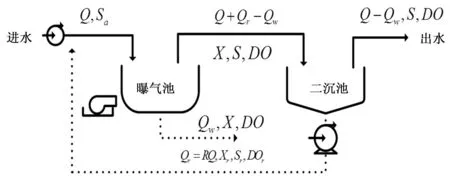
图2 AA/O工艺示意图
图中的系统参数意义如下:
Q,Qr,Qw分别表示进水,污泥回流和污泥排放流量(m3/d);
X,Xr为曝气池微生物浓度和回流污泥微生物浓度(mg/L);
Sa,S,Sr为进水与出水和回流污泥的底物浓度(mg/L);
DO为溶解氧浓度(mg/L);
V为生化池容积(m3);
R为污泥回流比。
对图中的系统的底物无知平衡以及微生物物质平衡可得活性污泥系统基本状态方程
(1)
(2)
其中:Kmax为底层物最大比利用速度常数;Kd为微生物的衰减率;Ks为饱和常数;Ko为氧的开关常数,它的取值反映了DO对Kma和Kd的影响;Y为产率系数。联立式(1)和(2),即为图2所示的以DO和Qw为控制变量,以S和X为状态变量的活性污泥系统的状态方程。
1.3污水处理优化函数建立
污水处理每日运行费用J,主要由剩余污泥处理费J1,回流污泥费用J2和曝气池供养费用J3组成:
(3)
一日内所需运行费用表示为J1=(单位污泥的处理费A)*(排放的污泥量)即

(4)
回流污泥费用J2=(单位污泥回流量所需费用B)*(污泥回流量Qr)即
(5)
曝气池供养费用J3=(转移单位质量氧所需费用C)*(总耗氧速度)即
(6)
其中:a为利用单位底物的需氧系数;Ds为溶解氧的饱和浓度最终建立的模型是以污泥排放量Qw和溶解氧浓度Do为控制变量,以污水处理每日运行费用J作为性能指标,并且把出水水质作为约束条件的系统。主要目的在于满足水质要求前提下减少运行成本为目的。根据污水厂实际运行情况分析,控制变量取值范围条件:其中每日有机物排放总量为Z(1),对方程约束条件为:
(8)
Zs为每日允许排放有机物总量,单位为mg(BOD)/L,Ds为溶解氧浓度最大值单位为mg/L。
2PSO-DE算法
2.1PSO算法描述
关于粒子运动轨迹的理论研究[7-8],PSO算法描述设搜索空间为D维,粒子的数量为M,第i个粒子的位置表示为:Xi=(xi1,xi2,...,xid);第i个粒子速度表示为:Vi=(vi1,vi2,...,vid);
本粒子的历史最优点表示为:Pi=(pi1,pi2,...,pid),所有粒子的历史最优点(全局最优点)表示为:Pg=(pg1,pg2,...,pgd)则第 i个粒子的速度和位置变化由下式进行更新:
vid(t+1)=wvid(t)+c1R(pid(t)-xid(t))+c2R(pgd(t)-xid(t))
(7)
粒子在通过以上运动方程作用运动,不断改变搜索轨迹,其运动速度增量与历史运动轨迹与群体运动轨迹相关,并且受到最大运动速度制约,从而在全局展开进行系统最优求解。但是随着进化代数的增加,粒子都向最优的方向发展,群体的多样性遭到破坏,这样就无法避免地产生了早熟收敛现象。
2.2避免粒子早熟方法
引入了DE算法,通过算法中的变异操作与交叉操作,使粒子多了一种对比与改变了最优粒子寻找轨迹[5]。
DE算法变异操作:对于个体Xi=(xi1,xi2,...,xid),变异后个体设为Yi=(yi1,yi2,...,yid),本文中采用优化性能最好的rand/1变异策略,通过变异策略后的公式即rand/1:yij=xr1,j+F(xr2,j-xr3,j),在研究与实际应用的被采用的也比较多。
DE算法交叉操作:对于变异个体Yi=(yi1,yi2,...,yid),操作如下:其中rand为 [0.1]随机数,交叉概率CR,如果rand≤CR,则新变异个体zij=xij,否则zij=yij。通过变异交叉的过程进行全局搜索求解,但前期的收敛速度缓慢,搜索效率低。
2.3改进型粒子群算法(PSD-DE)实现
新算法机理主要是利用了两者算法在前后期收敛速度上的表现,采用优势互补原理。对PSO的理论分析可以看出在进化初期有较好的收敛速度,随着进化代数增加,后期乏力收敛速度较缓,而对DE的理论分析可以看出进化初期收敛熟读较慢,随着进化代数增加,后期收敛速度比PSO有明显优势。对于新混合算法通过利用算法自适应交替优势进行,从而保证了在全局收敛速度。
新算法基本步骤:
Step1初始化:设置惯性权重w,种群规模M,加速因子C1和C2最大进化代数Tmax,步长因子F,交叉概率CR,随机初始化种群每个个体位置Xi=(xi1,xi2,...,xid)和每个个体的Vi=(vi1,vi2,...,vid)。
Step2计算每个个体的适应值,当前最优个体Pi=(pi1,pi2,...,pid),全局搜索最优个体为Pg=(pg1,pg2,...,pgd)。
Step3判断算法的终止条件(最大进化代数),如果满足则停止,输出最优个体为Pg=(pg1,pg2,...,pgd)。
Step4如果rand≤α(t),根据PSO算法更新个体位置Xi=(xi1,xi2,...,xid),否则,根据DE算法更新个体位置Xi=(xi1,xi2,...,xid)。
其中t为当前进化代数,rand为区间[0.1]随机数,F为适应值函数。
3仿真结果
首先为了测试PSO-DE的算法性能,通过3个典型优化测试函数来检验算法改进前后收敛性的变化,测试函数为:Sphere函数、Rosenbrock函数、Rastrigin函数。
对参数的设定为:50维空间,种群个数40,最大迭代次数限定为1000。测试结果如图3所示。
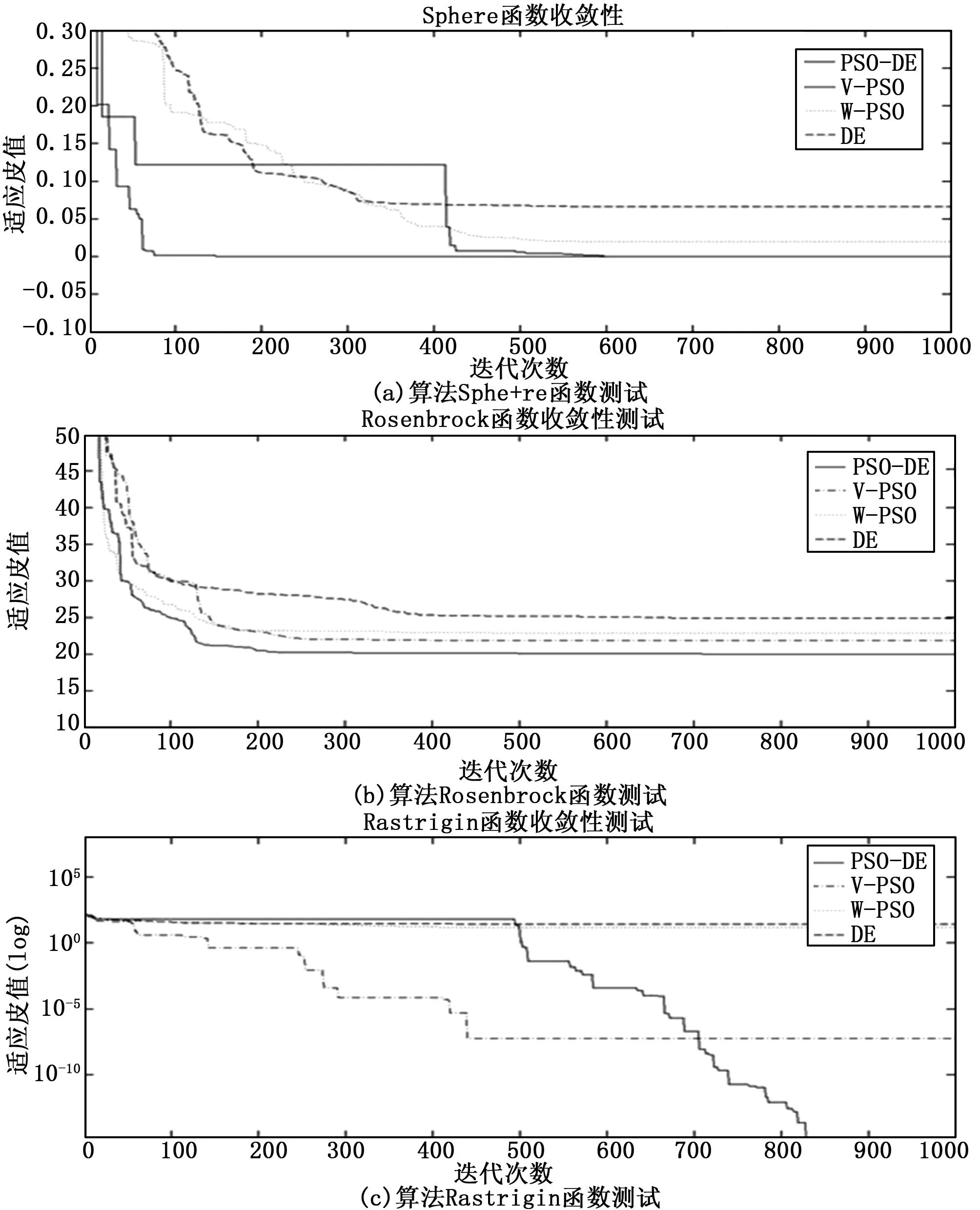
图3 4种算法在3种函数收敛性测试
从图5看出PSO-DE能够做到全局优化,而其它3种函数存在过早收敛或者收敛速度缓慢,存在陷入局部优化情况。

图4 溶解氧与污泥排放量优化曲线
在实际污水处理验证中选取了溶解氧浓度DO与污泥排放量Qw作为主要的控制变量,在算法中设定每个个体有两个参数构成,即由一个2维向量来表示,分别为XDO与XQw中m个的粒子求解对应Sij,Xij的解集,然后带入式(1)和(2)并在式(8)约束条件下求解Jmin问题。优化算法计算结果与未优化算法实际采集参数Q,X,S,DO进行比较。并计算了其中30天DO,Qw的运行情况并与优化后的数据进行对比,优化曲线如图4所示。在使用优化控制溶解氧的控制相比与未优化控制有了明显的改善,虽然在某几个阶段出现反常,可能算法陷入局部优化的情况,也可能外界干扰造成,但总体效果相比于未优化控制有了很大的提升,效率基本在90%以上。同样在排泥量方面优化后的情况出泥量有了明显提升,主要原因是在算法对工艺上的控制以及在回流污泥量方面有了优化改进,导致总的污泥排放量有了增加,但同样存在问题,在某几个阶段出现的下降,说明算法存在一定的缺陷,但总体效率控制在90%以上,运行30天结果优化后比未优化大幅度提升了出泥量。通过这两个主要控制变量的验证说明了算法的有效性。
4总结
本文通过对改进型混合粒子群算法PSO-DE 理论分析,建模,仿真,在污水处理中的工艺分析与能耗分析结合实际情况
考虑,仿真结果表明该算法相比普通的PSO改善了收敛早熟现象,提高了收敛精度,在实际污水处理中能在保证水质的前提下,进行降低能耗优化控制,具有良好泛化性,具有良好的实际应用价值。
参考文献:
[1]陈宏儒.城市污水处理厂能耗评价及节能途径研究[D].西安:西安建筑科技大学学报,2009.
[2]叶洪涛,罗飞,许玉格,等.基于新型免疫算法的污水处理过程最优控制[ J ].华南理工大学学报:自然科学版,2010,38(2): 137-141.
[3]郑广勇,罗飞,陈伟斌.基于免疫粒子群神经网络的污水水质预测微处理机[ J ]. 2010,31(2):75-77,81.
[4]吴亮红,王耀南,袁小芳,等.自适应二次变异差分进化算法[J]. 控制与决策,2006(8).
[5]马勇彭,永臻.城市污水处理系统实现全厂控制发展前景[J].中国给排水,2008(8):8-14.
[6]吴昌永.AA/O工艺脱氮除磷及其优化控制的研究[D].哈尔滨:哈尔滨工业大学市政环境工程学院,2010.
[7]倪瑞君.基于改进粒子群算法的输电网扩展规划研究[D].杭州:浙江大学,2013.
[8]李宁,孙德宝,邹彤,等.基于差分方程的PSO算法粒子运动轨迹分析[ J ].计算机学报,2006,29(11):2050-2062.
Optimal Control for Wastewater Treatment Process Based on Mixed POS-DE Algorithm
Ye Yongwei, Ge Shenhao, Ren Shedong, Qian Zhiqin
(Ministerial and Provincial Key Laboratory of E & M, Zhejiang University of Technology,Hangzhou310014, China)
Abstract:The characteristics of the sewage treatment process are higher energy consumption, poor treatment effect.To solve these problems the optimization control based on improved PSO algorithm is proposed. The new hybrid algorithm (PSO-DE)is designed to enhance the speed of particle and overcome prematurity. By establishing a corresponding model,taking dissolved oxygen concentration and sludge emissions as control variable, operating costs as performance index and outlet water quality as constraint conditions. The results show that the proposed algorithm can reduce the consumption of sewage treatment and keep the outlet water quality.
Keywords:sewage treatment process; optimization control; improved PSO algorithm
文章编号:1671-4598(2016)02-0068-03
DOI:10.16526/j.cnki.11-4762/tp.2016.02.018
中图分类号:TP277
文献标识码:B
作者简介:叶永伟(1964-),男,浙江义乌人,副教授、硕导,主要从事机电系统智能控制与制造业信息化方向的研究。
收稿日期:2015-07-30;修回日期:2015-09-21。

