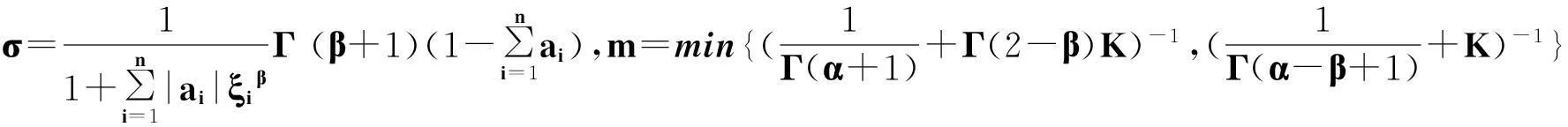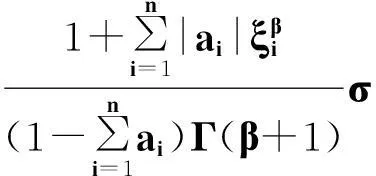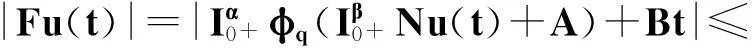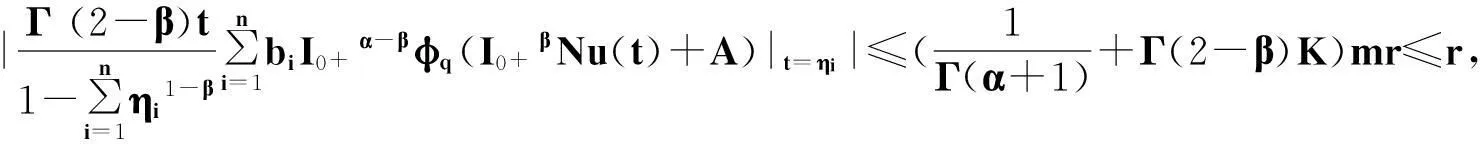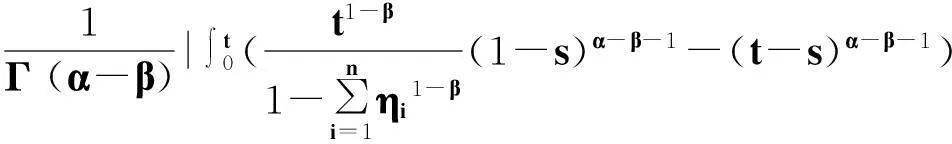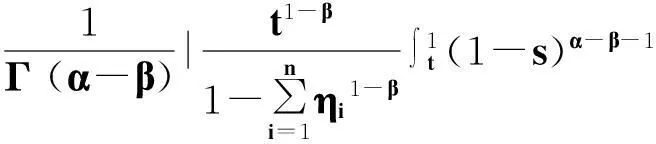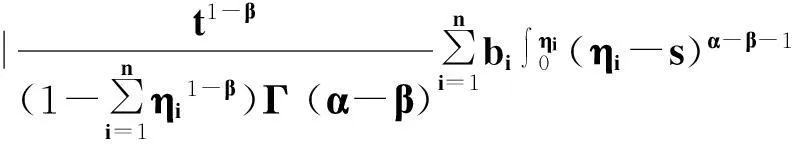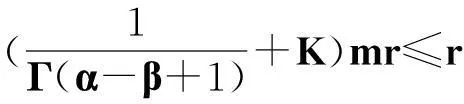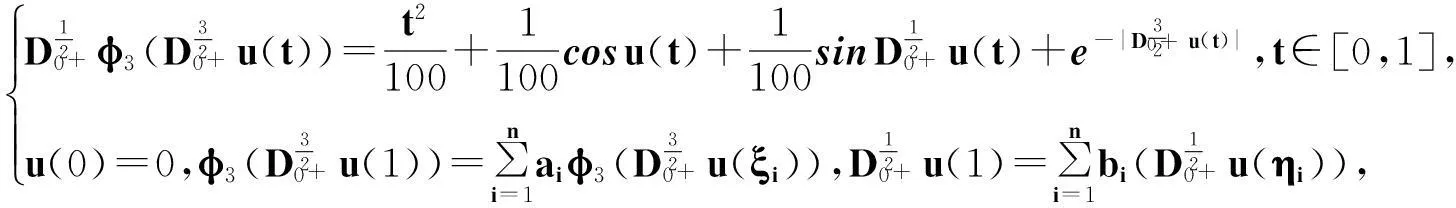带p-Laplacian算子的分数阶微分方程多点边值问题的解的存在性

吕秋燕,刘文斌,唐　敏*,申腾飞,程玲玲

(1.苏州市吴中区东山中学，中国 苏州　215107；2.中国矿业大学理学院，中国 徐州　221116)



带p-Laplacian算子的分数阶微分方程多点边值问题的解的存在性

吕秋燕1,刘文斌2,唐敏2*,申腾飞2,程玲玲2

(1.苏州市吴中区东山中学，中国 苏州215107；2.中国矿业大学理学院，中国 徐州221116)

摘要利用不动点定理,研究带有p-Laplacian算子的分数阶微分方程多点边值问题解的存在性,得到边值问题至少存在一个解的充分条件.

关键词分数阶微分方程;p-Laplacian算子;存在性;不动点定理

Exitence of Solutions for Fractions Multi-point Boundary Value Problem withp-Laplacian Operator

LVQiu-yan1,LIUWen-bin2*,TANGMin2,SHENTeng-fei2,CHENGLing-ling2

(1.Dongshan High School, Suzhou 215107, China;2.College of Science, China University of Mining and Technology, Xuzhou 221116, China)

AbstractThis paper presents a study on the existence of solutions for the fractional multi-point boundary value problem withp-Laplacian operator. Making use of the fixed-point theorem, we obtained sufficient conditions to guarantee the existence of at least one solution for the boundary value problem.

Key wordsfractional differential equation;p-Laplacian operator; existence; fixed point theorem

近年来,分数阶微分方程被广泛应用于物理学、生物学、控制论等诸多领域[1-3],因此,分数阶微分方程受到许多学者的广泛关注，并取得了很多有意义的结果.文献[4]研究了分数阶微分方程三点边值问题

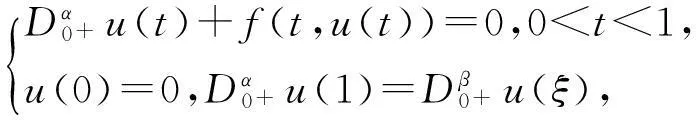
解的存在性,其中1<α≤2,0≤β≤1.

为了研究流体力学中相关问题,文献[5]介绍了一类带有p-Laplacian算子的微分方程,其一维形式如下

(φp(x′(t)))′=f(t,x(t),x′(t)),

(1)

文献[13]研究了下面分数阶微分方程反周期边值问题

受以上文献的启示,我们研究如下一类带有p-Laplacian算子分数阶微分方程多点边值问题解的存在性，

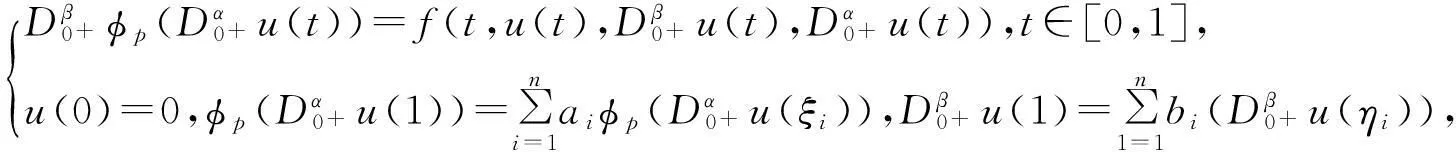
(2)

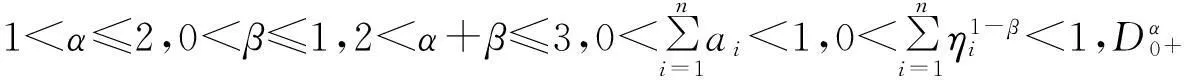
1基本定义和预备知识

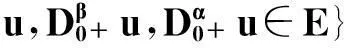
显然,E是Banach空间.

定义1.1[14]函数u:(0,∞)→R的α>0阶Riemann-Liouville型积分是指

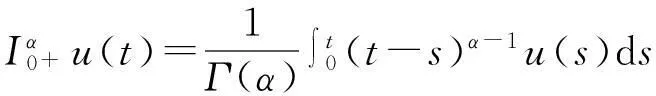
其中右边在(0,∞)上逐点定义.

定义1.2[14]函数u:(0,∞)→R的α>0阶Caputo型微分是指

其中n为大于或等于α的最小整数,右边是在(0,∞)上逐点定义的.

引理1.1[14]设函数u∈C(0,1)有α>0阶的Caputo型微分,则

其中n是大于或等于α的最小整数.

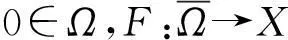
引理1.3设g(t)∈C[0,1]，

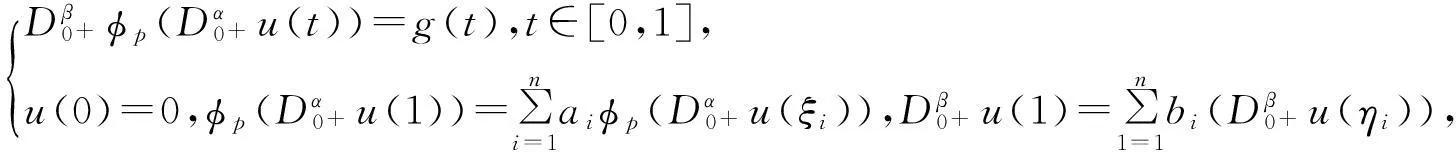
(3)

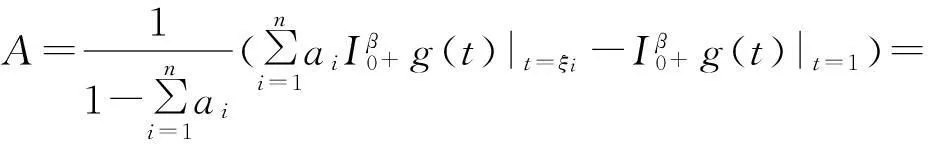
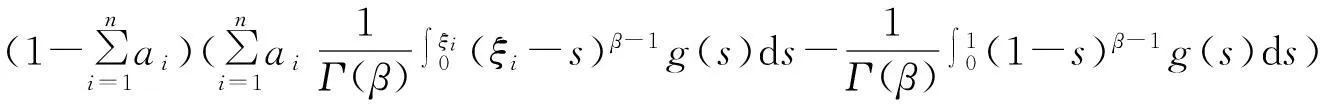
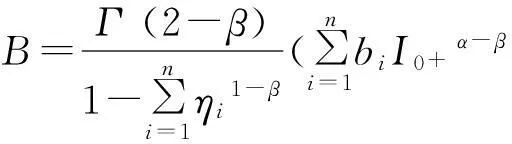
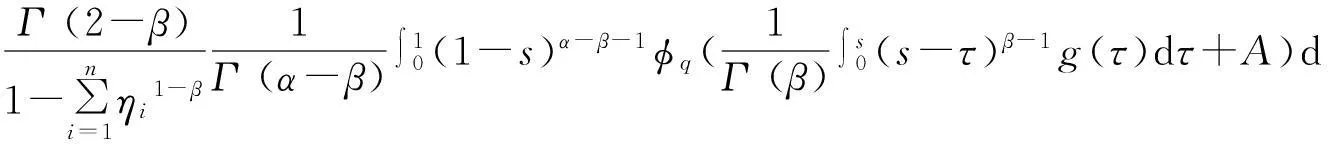
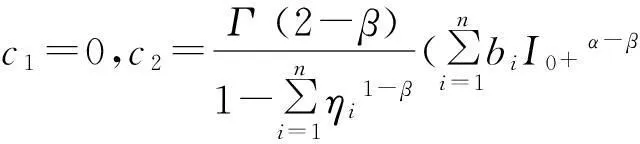
2主要结论

引理2.1算子F:E→E是全连续的.

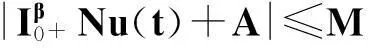
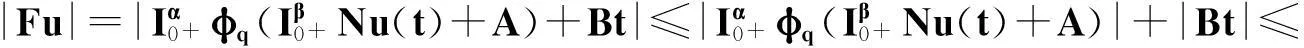
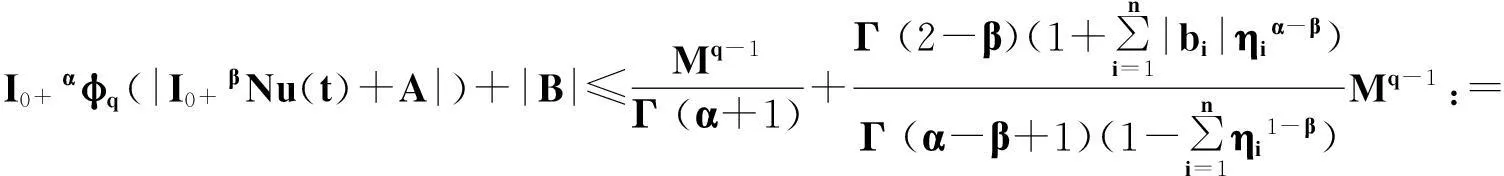
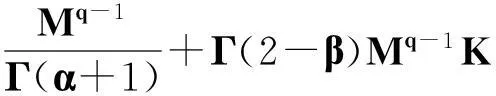
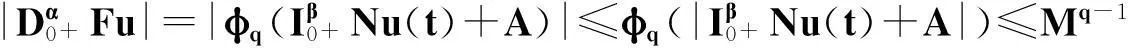
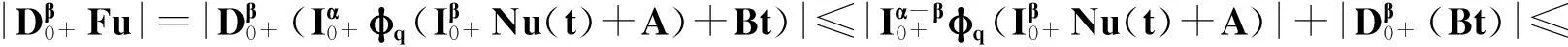
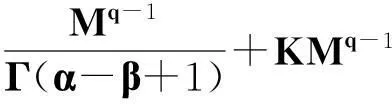
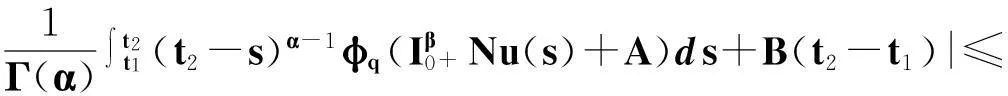
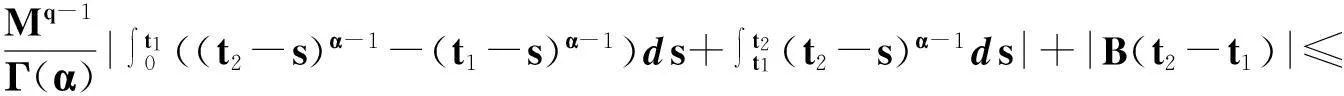
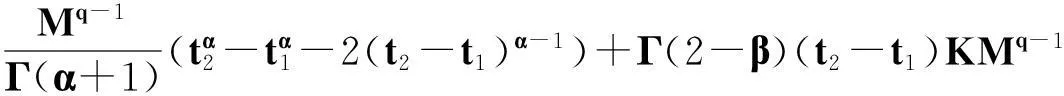
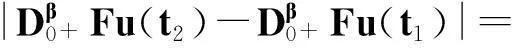
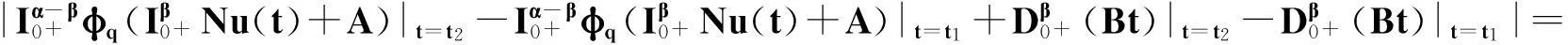
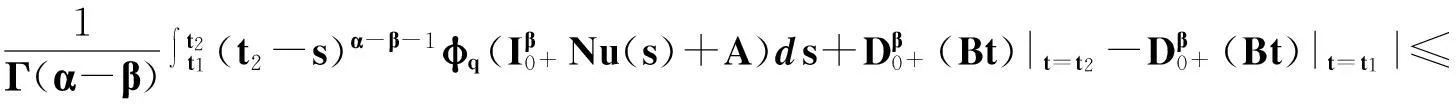
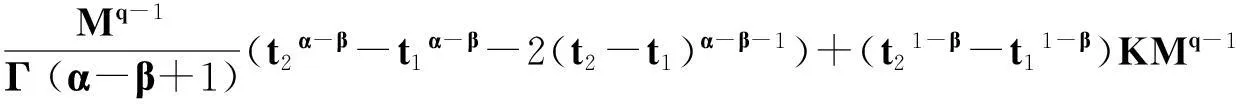
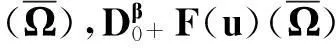
定理2.1对任意的常数r>0,Ω={u|‖u‖

(H)|f(t,u,v,w)|≤σφp(mr),

因此得到

由引理1.2知F满足Rothe条件,原方程至少存在一个解.

3例子

例3.1考虑如下带有p-Laplacian算子的分数阶微分方程多点边值问题

(4)

不妨设r=6,则有界集Ω={u‖|u‖E<6,u∈E}.

显然,问题(4)满足定理2.1的假设条件.因此,至少存在一个解.

参考文献：

[1]LAKSHMIKANTHM V. Theory of fraction functional differential equations[J]. Nonlinear Anal: TMA, 2008,69(10):33337-33343.

[2]ABDELKADER B. Second-order boundary value problems with integral boundary conditions[J]. Nonlinear Anal, 2009,70(1):364-371.

[3]DELBOSCO D. Fractional calculus and function spaces[J]. J Fract Calc,1994,6:45-53.

[4]LI C, LUO X, ZHOU Y. Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations[J]. Comput Math Appl, 2010,59(3):1363-1375.

[5]LEIBENSON L S. General problem of the movement of a compressible fluid in a porous medium[J]. Izvestiia Akademii Nauk Kirgizskoi SSR, 1945,9:7-10.

[6]SHEN T, LIU W, CHEN T,etal. Solvability of fractionalm-point boundary value problems withp-Laplacian operator at resonance[J]. Electr J Diff Equ, 2014(58):1-10.

[7]JIANG W. Solvability of boundary value problem withp-Laplacian at resonance[J]. Bound Value Probl, 2014(1):36.

[8]申腾飞,刘文斌,宋文耀.一类带有p-Laplacian算子分数阶微分方程边值问题正解的存在性[J]. 湖南师范大学自然科学学报, 2012,35(5):9-14.

[9]BAI Z. Positive solutions for boundary value problem of nonlinear fractional differential equation[J]. J Math Anal Appl, 2005,311(2):495-505.

[10]GE W. The existence of solutions ofm-point boundary value problems at resonance[J]. Acta Math Appl Sin, 2005,28(4):288-295.

[11]CHENG L, LIU W, YE Q. Boundary value problem for a coupled system of fractional differential equations withp-Laplacian operator at resonance[J]. Electr J Diff Equ, 2014(60):1-12.

[12]BAI Z. On positive solutions of nonlocal fractional boundary value problem[J]. Nonlinear Anal: TMA, 2010,72(2):916-924.

[13]CHEN T. An anti-periodic boundary value problem for the fractional differential equation withp-Laplacian operator[J]. Appl Math, 2012,25(11):1671-1675.

[14]BAI Z. Solvability for a class of fractional m-point boundary value problems at resonance[J]. Comput Math Appl, 2012,62(3):1292-1302.

[15]钟成奎.非线性泛函分析引论[M].兰州:兰州大学出版社,1998.

(编辑HWJ)

中图分类号O175.8

文献标识码A

文章编号1000-2537(2016)01-0080-05

*通讯作者,E-mail：wblium@163.com

基金项目：国家自然科学基金资助项目(11271364)

收稿日期：2013-12-02

DOI:10.7612/j.issn.1000-2537.2016.01.014