基于压缩感知的脉搏信号重构方法研究
【作 者】张爱华,欧继青,丑永新,杨彬
1 兰州理工大学电气工程与信息工程学院, 兰州市,730050
2 甘肃省工业过程先进控制重点实验室, 兰州市,730050
基于压缩感知的脉搏信号重构方法研究
【作 者】张爱华1,2,欧继青1,2,丑永新1,2,杨彬1
1 兰州理工大学电气工程与信息工程学院, 兰州市,730050
2 甘肃省工业过程先进控制重点实验室, 兰州市,730050
为了提高动态脉搏信号检测过程中信号存储和传输的效率,减少信号中的冗余,该文结合脉搏信号的稀疏性,提出一种改进的自适应匹配追踪算法。该算法在稀疏自适应匹配追踪算法的基础上,采用变步长和双阈值判别条件用于提高估计信号稀疏度的准确性。将所提出的算法用于建模的脉搏信号和实际采集的脉搏信号,结果表明:该算法能够快速、准确地估计信号稀疏度,具有良好的抗噪性。与现有的稀疏自适应匹配追踪算法和正交匹配追踪算法相比,该算法重构速度快、精度高。
压缩感知;匹配追踪;SAMP;脉搏信号
0 引言
随着嵌入式技术、传感器技术和无线通信技术的发展,各种小型的、便携的医疗设备广泛用于人体健康监护和疾病诊断。但对于一些便携式监护仪和无线远程医疗监护系统而言,由于存储空间和电池容量有限,若采用传统的信号采集方法,不仅会占用系统大量的存储空间,而且在数据存储和传输过程中会占用系统大量的处理时间,增加系统的功耗。与传统的采集方法相比,压缩感知技术同时进行数据采集和压缩[1-2],既节约了存储空间,也降低了功耗。由于压缩感知具有如此优点,已有学者将其应用于人体无线远程医疗监护系统[3-4]。赵曙光等[5]分析了DCT变换基下脉搏信号的稀疏特性,并且利用OMP和E-OMP算法对压缩后的脉搏信号重构。文献[6] 中采用Gabor变换进行稀疏化处理,并使用JOMP算法实现了多传感器脉搏信号重构。但是这些算法需要信号稀疏度信息,且对含噪的信号重构精度不高。因此,有学者提出了稀疏自适应匹配追踪算法(Sparse Adaptive Matching Pursuit, SAMP)[7]以及在其基础上的改进算法[8-9],可用于未知稀疏度信号的重构。但这些算法只用单一迭代停止条件,不能准确估计信号稀疏度,导致对较低信噪比信号重构精度不高。
针对上述这些算法的不足,本文利用脉搏信号的稀疏特性,提出了一种改进的自适应匹配追踪算法(Modified Adaptive Matching Pursuit,MAMP)。该算法在重构过程中使用变步长的方法[9]和双阈值判别条件—余量能量和余量能量变化率[10],快速、准确地恢复了原始脉搏信号。本文选用建模的信号验证所提方法的准确性和抗噪性并将此方法用于实际采集的脉搏信号。
1 方法
1.1 压缩感知原理
压缩感知的前提条件为信号是稀疏的或可压缩的,即信号中只含有少量的非零元素。然而,在时域内大多数信号不是稀疏的,但在一些变换域中是稀疏的或近似稀疏的,如Fourier变换、小波变换、DCT变换、Gabor变换等。对于长度为N的离散信号x,在某个正交基φi为N维列向量)下线性表示为:

式中Ψ为正交基,θ为稀疏信号。若θ中有K(K<<N)个数不为零,则称x是K稀疏信号。
测量矩阵是实现信号压缩的关键,在信号采集阶段通过M×N维的测量矩阵φ,可将N维信号x压缩为M(M<<N)维的y信号,如下式所示:
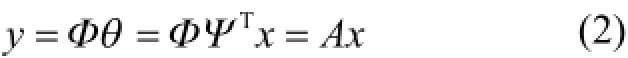
为了保证测量信号能被精确地重构出来,测量矩阵φ必须满足约束等距性质(RIP)[11]。但实际中判断一个矩阵是否满足RIP性质很难,故常用其等价形式[12],判断测量矩阵φ和稀疏变换基Ψ间的相关性,如下式所示:

式中相关系数μ(φ, Ψ)越小,则φ和Ψ间非相关性越大,重构后信号质量越高。
信号重构就是从测量信号y中恢复原始信号x,即求解线性方程组y=φθ,再通过反变换求出x。表面上看,由于未知数大于方程数,此方程无法求解。但是,由于θ是稀疏的,则可以通过最优l0范数的方法求解此方程,如下式所示:

式中,‖●‖l0表示向量θ中非零元素的个数。
1.2 改进的自适应匹配追踪算法
目前,大多数重构算法,如MP、OMP、BP算法等,需要信号稀疏度先验信息, SAMP算法对其进行了改进,采用余量能量作为迭代停止条件,实现了未知稀疏度信号重构。但也存在一些缺陷[8-9]:(1) 预选阶段原子过多,会造成预选原子错误且在候选阶段消耗大量的时间;(2) 固定步长不能准确地估计信号稀疏度;(3) 仅用单一迭代停止条件,不能准确估计信号稀疏度且在较低信噪比时,重构精度不高。
针对这些不足,本文提出了MAMP算法。在初选阶段,采用固定的阈值方案取代原来的选择方案(Sk=max(u, length))。每次只将u中最大的m个元素放入索引集Sk=max(u, m)。其中m为常数,u为余量与测量矩阵的内积。这样可避免因预选原子过多而造成的预选错误和后选集的时间消耗。为了能够准确地估计信号稀疏度,对SAMP算法的迭代停止条件和步长选择方法进行了改进,采用余量能量和余量能量变化率作为迭代停止条件;使用变步长的方法,当余量能量小于设定阈值时,步长置为1。MAMP算法基本步骤如下:
输入:测量信号y,测量矩阵φ,阈值ε1、ε2、ε3,步长l;
步骤1 初始化
余量r=y,支撑集长度length=l,m=30,阶段stage=1,迭代次数k=1,索引集S=∅,候选集C=∅,支撑集F=∅,θ=0;
步骤2 循环迭代
2) 计算索引集:将u中最大的前m个元素的下标加入索引集Sk=max(u, m);
4) 若 Ck的长度小于length不裁剪,Fnew=Ck,否则执行下一步进行裁剪;
5) 计算Ck中索引值对应原子与余量rk-1的相关系数,并取相关系数最大的length个原子存入Fnew;
骤2;
5) 更新支撑集Fk=Fnew,rk=rnew,k=k+1,转步骤2;
步骤4 输出计算
其中,符号“†”表示伪逆,“‖●‖2”表示2范数,rk为第k次迭代时的余量,Fk为第k次迭代时稀疏信号的支撑集,为观测矩阵子矩阵,由支撑集中下标所对应的列向量组成,θ为重构后的稀疏信号,x为重构后的信号。
2 实验数据
实际采集的脉搏信号受到噪声的干扰,无法获得脉搏信号的真值,实验中选用建模的脉搏信号验证方法的准确性和抗噪性。建模的脉搏信号由三个高斯函数合成,分别对应实际脉搏信号的主波、重搏前波和重搏波。每个高斯函数由幅值V、时间T和宽度U这3个参数确定[13],如下式所示:
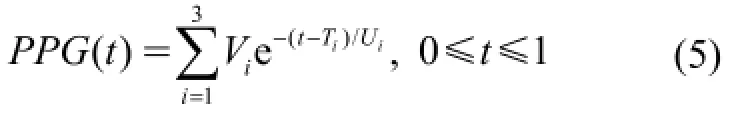
式中,V1=0.8, T1=0.25,U1=0.012,V2=0.5,T2=0.45,U2=0.01,V3=0.4,T3=0.7, U3=0.03。将(5)式产生的脉搏信号进行延拓,得到干净的脉搏信号x(t);若数据点间隔为1/250,则采样频率fs为250 Hz。为了消除信号幅值不同造成的影响,对其进行归一化(均值为0,方差为1)处理,具体如下式所示[14]:
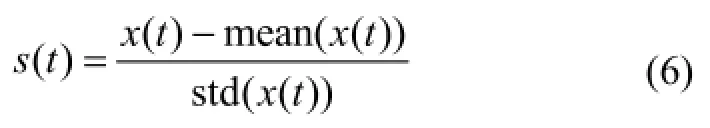
式中,mean(x(t))、std(x(t))分别为脉搏信号x(t)的均值和标准差,s(t)为归一化处理后的脉搏信号,如图1(a)所示。

图1 噪声污染前后的脉搏信号Fig.1 The PPG signals before and after noise pollution
此外,选用美国麻省理工学院PhysioNet/MIMIC数据库和课题组实际采集的脉搏信号。其中,MIMIC数据库收集了重症监护者的多种生理信号,包括脉搏信号、心电信号和血压信号等等,采样频率为125 Hz,采样时间为1 h;课题组脉搏信号由便携式多生理信号采集系统获得,采集对象为20~25岁的健康大学生,采样频率为1 kHz,时间为10 min。
选用PhysioNet/MIT-BIH / Noise Stress Test数据库的噪声信号[14],并加入建模的脉搏信号中,验证所提出方法的抗干扰性。噪声信号主要包括基线漂移和肌电干扰(含有工频干扰),采样频率为360 Hz,时间为1 h。
3 实验结果
3.1 方法的准确性分析
为了验证所提方法的准确性,选取建模的脉搏信号。首先采用DCT变换进行稀疏化处理,然后利用随机高斯矩阵进行数据压缩,最后采用所提出的MAMP方法进行信号重构。由于实验数据长度太长、所需要的观测数M过大,实验中采用滑窗的方法,每次以fs个数据点为窗口长度进行重构。实验中其他参数设置:阈值ε1,ε2,ε3分别为0.001、1×10-5、0.01;步长l为6;OMP算法的迭代次数k设置为35;窗口长度N=fs;观测数M=80。使用均方根误差(Mean Square Error, MSE)[14]评估所提出方法重构后信号的质量,如下式所示:

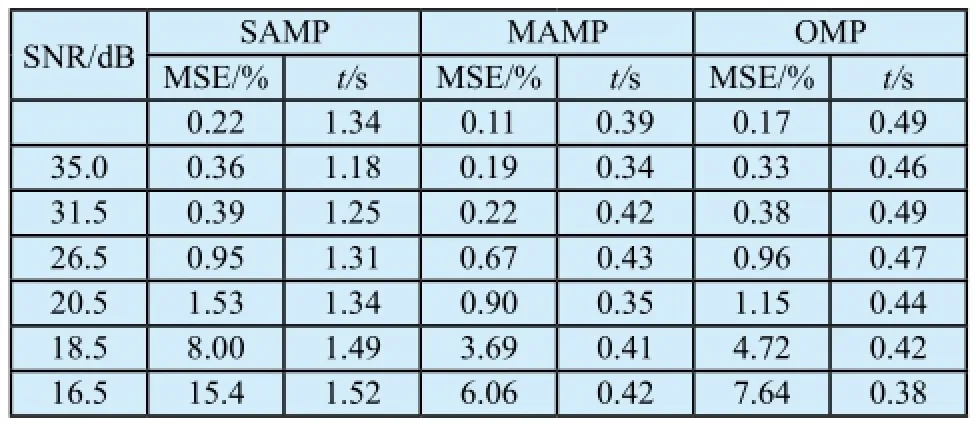
表1 不同信噪比下重构信号的MSE和tTab.1 The MSE and t of signals under various SNRs
3.2 方法的抗噪性分析
由于无法准确获得实际脉搏信号的信噪比(Signal Noise Ratio,SNR),实验中采用Noise Stress Test数据库提供的噪声与建模的脉搏信号s(t)叠加,产生的信号来验证MAMP算法的抗噪性[14]。噪声选用数据库中的基线漂移和肌电干扰信号,给其乘以不同的噪声系数[14]可以得到不同信噪比的脉搏信号,如表2所示。假设n(t)为噪声信号,则n(t)=a1·bw(t)+a2·ma(t);式中bw(t)为基线漂移,ma(t)为肌电干扰,a1、a2为噪声系数。为了消除脉搏信号和噪声采样频率不统一造成的影响,需要对噪声信号n(t)进行均匀降采样。然后截取长度相同的噪声信号n(t)加入s(t)得到含噪声的脉搏信号,通过下式计算信号的信噪比[14]:
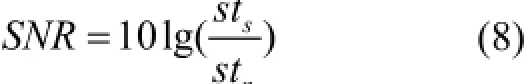
式中,sts为信号s(t)的方差,stn为信号n(t)的方差。

表2 噪声系数和信噪比关系Tab.2 The relationship of noise scale and SNR
表1中2至7行是不同噪声情况下重构信号的MSE和重构时间。从表1中可以看出随着信噪比的减小,各方法重构后信号的MSE值不断增大。其中,当信噪比大于26.5 dB时,MAMP、SAMP和OMP方法的MSE值不超过1.0%,受噪声影响较小;当信噪比小于26.5 dB时, 三种方法受噪声影响变化较大;16.5 dB(图1(b))时SAMP方法已超过10%,MAMP和OMP方法小于8%。采用式(8)计算不同信噪比下重构后信号的信噪比,如图2所示。
从图2中可以看出,随着信噪比的增大,各方法重构后信号的信噪比均增加且高于输入信号的信噪比,这是因为消除了部分干扰信号。由压缩感知原理可知,很难消除低频信号的影响,可以降低高频噪声的影响。在信噪比较低时,MAMP方法较其他两种方法明显提高了2~5 dB,因此验证了MAMP方法在较低信噪比能更准确估计信号稀疏度,抗噪性强。

图2 重构性能与信噪比关系Fig.2 The relationship of reconstructed performance and SNR
3.3 采样频率对方法的影响
为了分析采样频率对重构信号质量的影响,采用所提出的MAMP方法重构不同采样频率下的脉搏信号,结果如表3所示。SAMP方法的MSE值约为0.30%,时间在1.3 s左右;OMP方法的MSE值为0.1%~0.3%,时间为0.4~1.5 s;MAMP方法的MSE值为0.12%左右,时间约为0.35 s。从表3中可以看出,本文所提出的方法几乎不受采样频率的影响,其他两种方法重构的信号受到采样频率的影响较大。
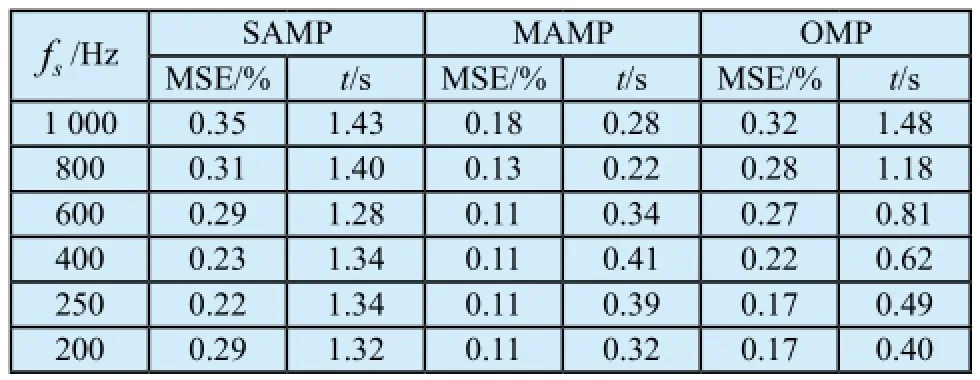
表3 不同采样频率下重构信号的MSE和tTab.3 The MSE and t under various sampling frequency
3.4 方法的应用
实验中选取PhysioNet/MIMIC数据库中20组病人数据(数据名称:208m~230m)和课题组采集的20名健康者的脉搏信号进行实验,结果分别如图3和图4所示。从图中可以看出,重构前后的脉搏信号非常相似,各拐点位置无明显变化,本文提出的方法能够用于脉搏信号的重构。
4 结论
针对现有的重构算法只用单一迭代停止条件,不能准确估计信号稀疏度和重构精度不高等问题,本文提出了MAMP方法。此方法能够自适应于信号的稀疏度,快速准确地恢复脉搏信号。实验结果表明,MAMP算法受信号采样频率影响小,重构速度快,能够准确地重构出脉搏信号,且在较低信噪比时重构精度高。

图3 MIMIC数据库脉搏信号重构结果Fig.3 The reconstructed results of MIMC database signal

图4 课题组采集的脉搏信号重构结果Fig.4 The reconstructed results of acquisition signal
[1] Jin J, Gu YT, Mei SL. A stochastic gradient approach on compressive sensing signal reconstruction based on adaptive filtering framework [J]. IEEE J Select Topics Sign Proc, 2010, 4(2): 409-420.
[2] 余凯, 李元实, 王智, 等. 基于压缩感知的新型声信号采集方法[J].仪器仪表学报, 2012, 33(1): 105-112.
[3] Craven D, McGinley B, Kilmartin L, et al. Compressed sensing for bioelectric signals: a review[J]. IEEE J Biomed Health Inform,2015, 19(2): 529-540.
[4] Zhang Z, Jung TP, Makeig S, et al. Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware[J]. IEEE Trans Biomed Eng, 2013, 60(1): 221-224.
[5] 康如婷, 赵曙光, 刘浩. 一种高效的PPG压缩感知重构算法[J]. 计算机工程与应用, 2014, 50(14): 131-134.
[6] Hu FY, Li SS, Xue T, et al. Design and analysis of low-power body area networks based on biomedical signals[J]. Int J Electron, 2012, 99(6): 811-822.
[7] Do TT, Lu G, Nguyen N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Conf Sign Syst Comput, 2008, 581-587.
[8] 甘伟, 许录平, 罗楠, 等. 一种自适应压缩感知重构算法[J]. 系统工程与电子技术, 2011, 33(9): 1948-1953.
[9] 朱延万, 赵拥军, 孙兵. 一种改进的稀疏度自适应匹配追踪算法[J]. 信号处理, 2012, 28(1): 80-86.
[10] 吕方旭, 张金成, 王泉, 等. 基于傅里叶基的自适应压缩感知重构算法[J]. 北京航空航天大学学报, 2014, 30(4): 544-550.
[11] Candes E. The restricted isometry property and its implications for compressed sensing[J]. Comput Rendus Math, 2008, 346(9/10): 589-592.
[12] Baraniuk R, Davenport M, Devore R, et al. A simple proof of the restricted isometry property for random matrices[J]. Construct Approximat, 2008, 28(3): 253-263.
[13] 张爱华, 胡文龙, 丑永新. 基于循环平稳算法的脉搏信号质量评估与滤波[J]. 中国医疗器械杂志, 2015, 39(2): 83-86.
[14] 丑永新, 张爱华, 杨晓华. 基于改进滑窗迭代DFT的动态脉率变异性提取[J]. 仪器仪表学报, 2015, 36(4): 812-821.
Research on PPG Signal Reconstruction Based on Compressed Sensing
【 Writers 】ZHANG Aihua1,2, OU Jiqing1,2, Chou Yongxin1,2, YANG Bin1
1 College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou, 730050,
2 Key Laboratory of Gansu Advanced Control for Industrial Processes, Lanzhou, 730050
compressed sensing, matching pursuit, sparse adaptive matching pursuit, photoplethysmography signal
R318.6;TN911.7
A
10.3969/j.issn.1671-7104.2016.01.002
1671-7104(2016)01-0005-05
2015-09-14
国家自然科学基金资助项目(81360299);甘肃省自然科学基金资助项目(145RJZA065);模式识别国家重点实验室开放课题(201407347)。
张爱华,教授,博士生导师,E-mail: lutzhangah@163.com
【 Abstract 】In order to improve the storage and transmission efficiency of dynamic photoplethysmography (PPG) signals in the detection process and reduce the redundancy of signals, the modified adaptive matching pursuit (MAMP) algorithm was proposed according to the sparsity of the PPG signal. The proposed algorithm which is based on reconstruction method of sparse adaptive matching pursuit(SAMP), could improve the accuracy of the sparsity estimation of signals by using both variable step size and the double threshold conditions. After experiments on the simulated and the actual PPG signals, the results show that the modified algorithm could estimate the sparsity of signals accurately and quickly, and had good anti-noise performance. Contrasting with SAMP and orthogonal matching pursuit(OMP), the reconstruction speed of the algorithm was faster and the accuracy was high.

