基于时滞分割方法的VTOL直升机鲁棒非脆弱H∞控制
惠俊军,张合新,陈 伊,李 明
(1.陕西省宝鸡市150信箱11分箱,陕西 宝鸡 721013;2.火箭军工程大学,西安 710025)
基于时滞分割方法的VTOL直升机鲁棒非脆弱H∞控制
惠俊军1,张合新2,陈 伊1,李 明1
(1.陕西省宝鸡市150信箱11分箱,陕西 宝鸡 721013;2.火箭军工程大学,西安 710025)
针对含有飞行时滞的垂直起降(VTOL)直升机系统设计了时滞相关鲁棒非脆弱H∞控制器。基于时滞中点值把时滞区间均分为两部分,针对每一分割区间构造新的Lyapunov-Krasovskii (L-K)泛函,并结合L-K稳定性定理、积分不等式方法和自由权矩阵技术,建立了新的基于线性矩阵不等式(LMI)形式的时滞相关有界实(BRL)条件。在此基础上设计了该系统的非脆弱H∞控制器,通过求解线性矩阵不等式的可行解得到控制器的参数化表达式。最后应用于VTOL直升机的飞行控制仿真表明,所设计的控制器具有更好的鲁棒性和非脆弱性。
非脆弱;H∞控制;Lyapunov-Krasovskii泛函;时滞分解;线性矩阵不等式
0 引言
时滞现象常存在于导弹的制导、飞行器的控制与航空航天系统当中,它的存在一方面使得系统的分析与控制器的设计变得复杂,另一方面可以导致系统性能恶化甚至不稳定。近年来,时滞系统的稳定性分析与控制问题成为控制理论研究的热点问题[1-2]。
VTOL直升机的垂直起降控制是一种典型的含有时滞的动态控制系统。在实际的飞行控制当中,常规的鲁棒控制器设计方法(如H∞、H2和μ综合),仅考虑系统参数的不确定性,而没有考虑控制器本身参数的不确定性。然而,在实际控制器的实现中,由于硬件(如A/D、D/A转换)、软件(如计算截断误差)等原因,使得控制器存在一定的不确定性[3]。Keel等[4]指出,当控制器参数存在摄动时,常规的鲁棒控制器表现出高度的脆弱性,从而造成闭环系统的性能下降甚至控制器失效。所以对非脆弱控制器的研究引起人们的关注[5-12]。文献[5-8]和文献[9-12]分别针对时滞系统的非脆弱H∞控制问题和非脆弱保性能控制问题进行了深入研究。在这些研究中,主要围绕如何降低所得结论的保守性和满足一定的性能指标而展开。就研究方法而言,主要有自由权矩阵方法、积分不等式方法和时滞分割方法等。在上述方法中,自由权矩阵方法和时滞分割方法有利于降低结论的保守性;然而,这两种方法都会随着引入过多矩阵变量和分割数的增大而增加计算负担,且不利于控制器的设计。积分不等式方法形式简单,含矩阵变量较少,利于理论分析和计算;然而如何构造缩放程度较小的不等式是一个难题。在兼顾结论的保守性、计算的复杂性和控制器的实现上,Lyapunov-Krasovskii (L-K)泛函和界定条件的合理选取成为目前研究的一个重点问题。
本文主要采用时滞分割和积分不等式相结合的处理方法,研究了VTOL直升机的非脆弱H∞控制问题。首先通过时滞分割构造适当的L-K泛函并结合积分不等式方法,建立时滞相关有界实(BRL)条件,在此基础上设计了非脆弱控制器。最后把该控制器应用于VTOL的飞行控制当中,仿真结论表明了设计方法的有效性,相比一般鲁棒控制器具有更好的镇定效果和明显的非脆弱性。
1 问题描述
某型VTOL直升机动态运动的线性化数学模型可描述如下[13]:
(1)
其中,x(t)=[vh,vv,q,θ]T为系统状态向量,vh、vv、q、θ分别是VTOL直升机的水平速度、垂直速度、俯仰角速率和俯仰角。u(t)为控制向量,z(t)为被调输出,ω(t)为扰动输入向量。h(t)为时变连续的函数且满足
(2)
针对系统(1)定义如下性能指标
(3)
其中,γ>0为给定标量。本文主要目标是针对外部干扰作用下的系统(1),设计一个状态反馈非脆弱H∞控制器
u(t)=(K+ΔK)x(t)
(4)
其中, K为控制器增益;ΔK为增益摄动,并满足
(5)
使得满足以下两个条件:
1)ω(t)=0时,由(4)构成的闭环系统(1)渐近稳定;
2)对于给定的γ>0,在零初始条件下对于‖z(t)‖2<γ2‖ω(t)‖,ω(t)∈L2[0,∞]。
把非脆弱控制器(4)代入系统(1),则闭环系统为:
(6)
其中,Ak=A+BuK+BuΔK,Ck=C+DuK+DuΔK。
为了证明方便,首先给出如下引理。
引理1[14].对于任意定常矩阵W∈n×n,W=WT>0,标量h:=h(t)>0和向量函数n,以下相关积分项有定义,则有:
其中,

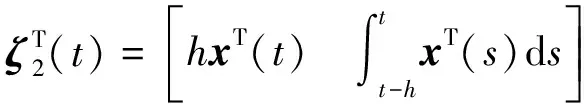
引理2[15].设h1≤h(t)≤h2,其中h(t):+→+,那么,对于任意的R=RT>0,下面的不等式成立
其中,

引理 3[16].假设γ1≤γ(t)≤γ2,其中γ(·):+→+,那么,对于任意适当维数的常数矩阵Ξ1、Ξ2和Ω,下面的矩阵不等式成立
Ω+(γ(t)-γ1)Ξ1+(γ2-γ(t))Ξ2<0
当且仅当
Ω+(γ2-γ1)Ξ1<0,Ω+(γ2-γ1)Ξ2<0
引理4[17].给定具有适当维数的矩阵Q=QT,H,E,则有Q+HF(t)E+ETF(t)THT<0,对任意满足F(t)TF(t)≤I的F(t)成立的充要条件是存在ε>0,使得
Q+ε-1HHT+εETE<0
2 时滞相关有界实引理(BRL)

(7)
(8)








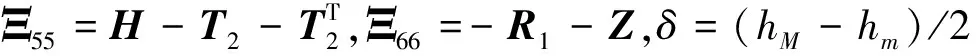




证明:首先基于时滞中点值hδ,把时滞区间[hm,hM]均分成两部分,即[hm,hδ]和[hδ,hM]。
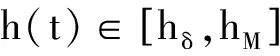
V1(t)=V11(t)+V12(t)+V13(t)
(9)
其中


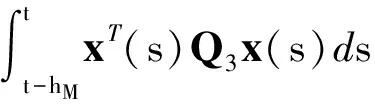


取泛函沿系统(6)的导数有
xT(t-hδ)Q1x(t-hδ)-
(1-μ)xT(x-h(t))Q2x(t-h(t))-
xT(t-hM)Q3x(t-hM)-

(10)
其中,W、H为定理1所定义。由积分不等式可得:
(11)
(12)
由引理1和引理2分别有
(13)
(14)

(15)
另一方面,由系统(6)有以下恒等式
(16)
其中,T1、T2为适当维数的自由权矩阵。
把式(11)~式(16)代入式(10)中,并定义增广向量

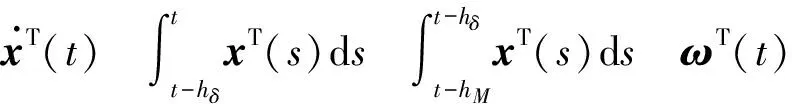
(17)
其中
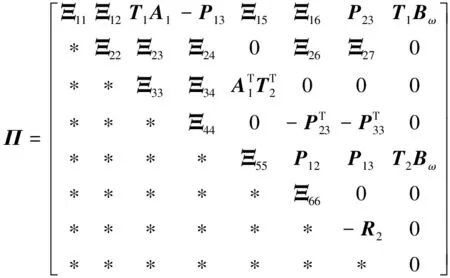
对于给定的γ,考虑性能指标J(ω),则把z(t)Tz(t)-γ2ωT(t)ω(t)加到不等式(17)两边,可得
(18)
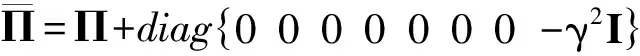


(19)
那么
(20)
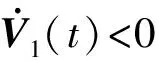
V(t)|t=0<0
(21)
即‖z(t)‖<γ‖ω‖2,从而闭环系统在零初始条件下具有给定的H∞扰动抑制水平γ。

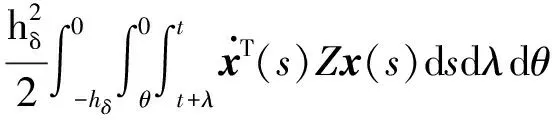
其中,

(22)
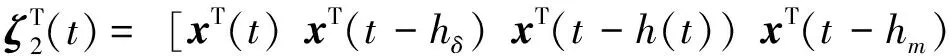
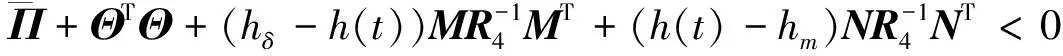
(23)
那么
(24)
从而闭环系统在零初始条件下具有给定的H∞扰动抑制水平γ。
由于hM-hδ=hδ-hm=δ,对式(19)或式(23)应用引理3以及Schur补,即可得定理1中的式(7)和式(8)。
3 H∞非脆弱控制器的设计
本节在第2节BRL的基础上,设计非脆弱H∞控制器。

(25)
(26)
则系统(1)在非脆弱控制器(4)的作用下不仅渐近稳定,而且在零初始条件下具有给定的H∞扰动抑制水平γ,且控制器增益K=YX-T。其中,

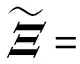
XAT+YTBT,
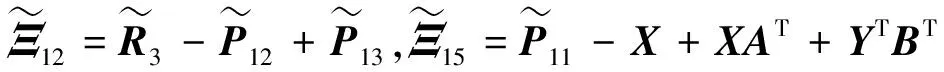

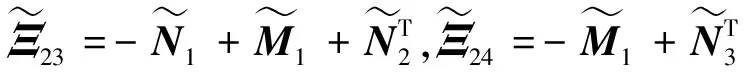



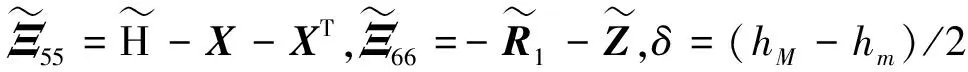

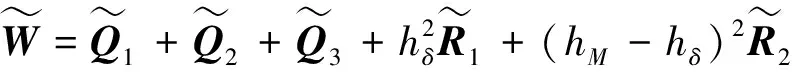

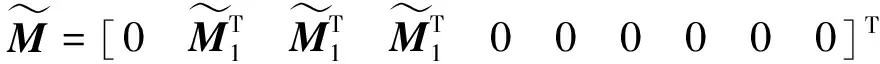


证明:由于定理1中式(7)和式(8)给出的条件为非线性矩阵不等式,不能直接得到控制器的解。下面给出控制器的设计方法,首先将式(7)和式(8)中的不确定项(即含ΔK项)分离,即
(27)
(28)
其中

(29)
(30)
其中


进而对式(29)和式(30)应用Schur补可得
(31)
(32)
令T1=T2=X-1,其中X为非奇异矩阵,对式(31)和式(32)两边左乘Ψ,右乘其转置,其中

4 设计实例



当不加外部控制(即u(t)=0)时,该系统的开环响应曲线如图1所示,显然系统是不稳定的。
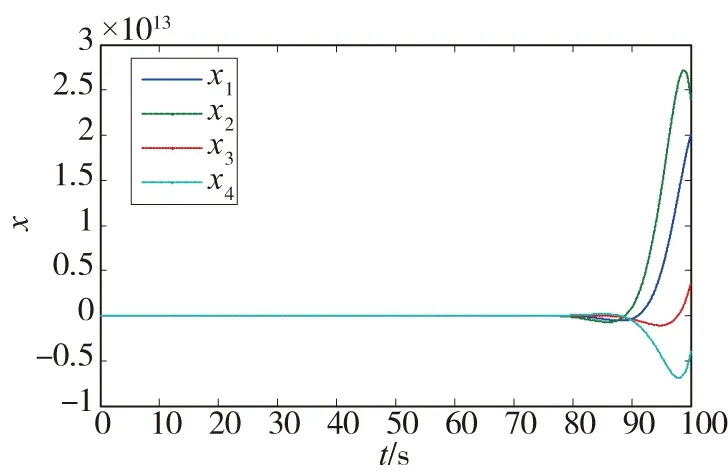
图1 VTOL系统状态开环响应曲线Fig.1 Response of state with the open-loop system of VTOL
下面分析系统在控制器作用下的镇定性能。设时滞下界hm=0,首先在无外部干扰和控制器增益摄动的情况下设计控制器。当hM=7时,由定理1可求得状态反馈矩阵为

将其代入系统方程可得系统各状态响应曲线,如图2所示。

图2 VTOL系统状态闭环响应曲线Fig.2 Response of state with the closed-loop system of VTOL
可见在控制器的作用下,系统各状态很快收敛,且具有较好的稳定性能。
为了进一步分析控制器的非脆弱性能。假设在幅值0.1的正弦干扰和控制器增益摄动的情况下,针对hM=7的定常时滞进行仿真,其中摄动参数取为:

扰动矩阵Fa∈R2×2,则由定理2可求得最小的干扰抑制水平γ=0.9716,相应的控制增益矩阵为
在非脆弱控制器K1的作用下,系统状态响应曲线如图3所示。

图3 鲁棒非脆弱控制器下系统状态响应曲线Fig.3 Response of state with robust non-fragile controller
当控制器不存在增益摄动时(即设摄动参数Da和Ea为零),同样取γ=0.9716,由定理2可得一般鲁棒控制器增益矩阵
相应的系统状态响应曲线如图4所示。

图4 一般鲁棒控制器下系统状态响应曲线Fig.4 Response of state with robust controller
以状态x1(t)为研究对象,图5给出了在相同条件下,非脆弱控制器和一般鲁棒控制器下的镇定效果比较。

图5 不同控制器作用下的状态x1响应曲线Fig.5 Response of state x1with different controller
由图3~图5可以看出,当存在控制器增益摄动时,非脆弱控制器K1与一般控制器K2相比,系统状态在控制器K1的作用下,能够满足一定的性能指标,且容许控制器增益的摄动;而在K2的作用下表现出明显的脆弱性,系统状态振荡较大,收敛较慢。
5 结论
本文针对含有飞行时滞的VTOL直升机系统设计了鲁棒非脆弱H∞控制器。通过设计L-K泛函并结合LMI的方法得到了系统稳定的BRL条件和非脆弱控制器。该控制器无需任何的参数调整和迭代处理即可求解。将控制器应用于VTOL直升机的飞行过程,仿真过程表明了所设计的控制器相比一般鲁棒控制器具有更好的镇定性能和非脆弱性。
[1]GuK,KharitonovVL,ChenJ.Stabilityoftime-delaysystems[M].Basel:Birkhauser, 2003: 1-17.
[2]RichardJP.Time-delaysystems:anoverviewofsomerecentadvancesandopenproblems[J].Automatica, 2003,39(10):1667-1694.
[3] 王武,杨富文.不确定时滞系统的时滞依赖鲁棒非脆弱H∞控制[J]. 控制理论与应用,2003,20(3):473-476.
[4]KeelLH,BhattacharyyaSP.Robust,fragile,oroptimal[J].IEEETransactionsonAutomaticControl, 1997,42(8):1098-1105.
[5] 吴敏,肖伸平,张先明,等.中立型系统的时滞相关非脆弱H∞控制[J]. 系统工程与电子技术,2008,30(9):1768-1773.
[6]WangC,ShenY.Delay-dependentnon-fragilerobuststabilizationandH∞controlofuncertainstochasticsystemswithtime-varyingdelayandnonlinearity[J].JournaloftheFranklinInstitute,2011, 348(8):2174-2190.
[7]ZhangJH,ShiP,YangHJ.Non-fragilerobuststabilizationandH∞controlforuncertainstochasticnonlineartime-delaysystems[J].Chaos,SolitonsFractals, 2009,42 (5):3187-3196.
[8]YangJ,ZhongSM,XiongLL.Adescriptorsystemapproachtonon-fragileH∞controlforuncertainfuzzyneutralsystems[J].FuzzySetsandSystems,2009, 160 (4) :423-438.
[9] 付兴建,刘小河.带不确定时滞的中立型系统之鲁棒非脆弱保性能控制[J].控制理论与应用,2008,25(5):938-942.
[10] 李涛,张合新,孟飞.一类分布时滞不确定系统的鲁棒非脆弱保性能控制器设计[J].控制与决策,2011,26(10):1520-1524..
[11]LienCH.Non-fragileguaranteedcostcontrolforuncertainneutraldynamicsystemswithtime-varyingdelaysinstateandcontrolinput[J].Chaos,SolitonsandFractals,2007,31(4):889-899.
[12]KimJH.Delay-dependentrobustandnon-fragileguaranteedcostcontrolforuncertainsingularsystemswithtime-varyingstateandinputdelays[J].InternationalJournalofControl,Automation,andSystems2009, 7(3):357-364.
[13]ParlakciMN.Improvedrobuststabilitycriteriaanddesignofrobuststabilizingcontrollerforuncertainlineartime-delaysystems[J].InternationalJournalofRobustandNonlinearControl, 2006, 16(13): 599-636.
[14]ZhangXM,HanQL.Adelaydecompositionapproachtodelay-dependentstabilityforlinearsystemswithtime-varyingdelays[J].InternationalJournalofRobustandNonlinearControl,2009,19(17):1922-1930.
[15]RamakrishnanK,RayG.Delay-range-dependentstabilitycriterionforintervaltime-delaysystemswithnonlinearperturbations[J].InternationalJournalofAutomationandComputing,2011,8(1): 141-146.
[16]YueD,TianEG,ZhangYJ.Apiecewiseanalysismethodtostabilityanalysisofcontinuous/discretesystemswithtime-varyingdelay[J].InternationalJournalRobustNonlinearControl, 2009,19(13): 1493-1518.
[17]PetersenIR,HollotCV.ARiccatiequationapproachtothestabilizationofuncertainlinearsystems[J].Automatica, 1986, 22(4): 397-411.
A Delay Decomposition Approach to Robust Non-fragileH∞Control for VTOL Helicopter
HUI Jun-jun1,ZHANG He-xin2,CHEN Yi1, LI Ming1
(1. MailBox 150 Extension 11, Baoji Shanxi 721013, China;2. The Rocket Force Engineering university ,Xi’an 710025,China)
The delay-dependent robust non-fragileH∞controller for a vertical taking-off and landing (VTOL) helicopter system with flight time-delays is investigated. Based on the delay decomposition method, the whole delay interval is divided into two equidistant subintervals at its central point and new Lyapunov-Krasovskii (L-K) functionals are introduced on these intervals. Then, by using L-K stability theorem , integral inequality method together with free weighting matrix approach, a new delay-dependent BRL is formulated in terms of linear matrix inequality. Based on this, non-fragileH∞controller is designed for this system. At last, simulation results show that the designed controller has good robust and non-fragile performance.
Non-fragile;H∞control;Lyapunov-Krasovskii(L-K)functional; Delay decomposition approach; Linear matrix inequality
10.19306/j.cnki.2095-8110.2016.06.007
2016-02-14;
2016-03-07。
惠俊军(1977 - ),男,博士,工程师,主要从事飞行器控制方面的研究。E-mail: ep22stone@163.com
TP13
A
2095-8110(2016)06-0033-07

