基于改进PSO算法的红外气体传感器温度补偿

毛琪波，余震虹，王相淳



基于改进PSO算法的红外气体传感器温度补偿

毛琪波1，余震虹1，王相淳2

（1.江南大学 物联网工程学院，江苏 无锡 214122；2.浙江大学 电气工程学院，浙江 杭州 310000）

针对红外型气体传感器测量精度受环境温度影响较大的问题，提出一种基于嵌入自适应列维变异的动态拓扑免疫粒子群-最小二乘支持向量机（DLIPSO-LSSVM）温度补偿算法。DLIPSO算法在粒子群优化过程中采用动态拓扑Dbest机制以更好地适应粒子群进化过程；为确保粒子多样性，平衡局部搜索与全局搜索，算法嵌入自适应列维变异对粒子进行变异。利用基准测试函数对DLIPSO算法进行性能对比评价，仿真结果表明算法具有较强的全局搜索能力、精度高且稳定性较好。利用DLIPSO算法对LS-SVM的参数进行优化，将混合算法用于实际红外气体传感器的温度补偿，实验数值结果表明算法可将补偿结果的相对误差控制在5%范围内。

红外气体传感器；温度补偿；粒子群优化；动态拓扑；列维变异；数值仿真

0 引言

目前已经发展起多种实现对气体定性及定量分析检测技术，主要包括基于电化学原理、催化燃烧式原理和红外光谱吸收原理等等[1]。现阶段来说，采用基于红外光谱吸收原理的红外型气体传感器是较精确的检测方法，具有不易老化、精度高、性能稳定等优点，已成为当前气体传感器的研究热点之一[2]。但红外气体传感器在工作时对实际环境的温度相当敏感，对其进行温度补偿是至关重要的。常用的气体传感器温度补偿方法可分为2种，即硬件补偿和软件补偿，其中软件补偿主要包括最小二乘曲线拟合法、多段折线逼近法以及神经网络等[3]。

粒子群优化（particle swarm optimization，PSO）算法因其建模简单，收敛速度快且易于实现等优点，在求解组合优化问题、模式分类、传感器网络、生物分子研究等领域得到了广泛的应用[4]。针对标准PSO算法易陷入早熟、局部最优的不足，提出一种新的嵌入自适应列维变异的动态拓扑免疫粒子群优化（DLIPSO）算法，该算法将在粒子群优化过程中引入动态拓扑Dbest机制，将种群动态划分为多个子种群，子种群中的探索粒子不仅受到全局最优粒子的影响，而且受到该子种群中局部最优粒子的影响，能更好地适应粒子群进化过程；在新抗体的产生过程中，引入自适应列维变异（Levy mutation）来提高算法的随机性并保持粒子多样性；实验结果表明DLIPSO算法具有较高的收敛效率和优化性能。利用DLIPSO算法对最小二乘支持向量机（LS-SVM）进行优化，可寻找预测模型结构风险计算式中的正规化参数和核宽度数的最优值，其对于模型结构的逼近能力和复杂度都有很大的影响。数值仿真结果表明本文提出的红外气体传感器温度补偿模型具有较好的温度补偿效果。

1 系统设计

1.1 红外气体传感器工作原理分析

红外气体光谱吸收法是利用不同的气体分子对红外光具有特征红外吸收峰这一特性来实现的。气体对于红外光能量的吸收程度除了与光在物质中经过的路程有关，还和其浓度有关，它们之间的关系符合Lambert-Beer定律，如式(1)所示：

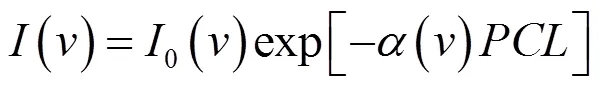
式中：()为气体在频率处的吸收系数；为吸收气体的体积浓度百分比；为总的气体吸收光程；为压强。

1.2 系统组成

所采用的气体采集系统结构如图1所示。首先利用信号调理电路将气体传感器和温度传感器采集到的信号进行滤波、放大；再将信号调整到合适范围后输入到单片机；信号在单片机内进行模数转换后，经串口发送到PC机，最后在PC机内可以完成数据处理、温度补偿等功能。根据红外气体检测的基本理论，系统采用双通道气体浓度检测方法。利用热释电晶体晶片式探测器实现光强度的测量，用两个不同波带区域内的单元测试器来实现，可以消除发光光源输出功率不稳定和探测器响应灵敏度变化等影响，并且解决了实际光强度难以测量的问题。

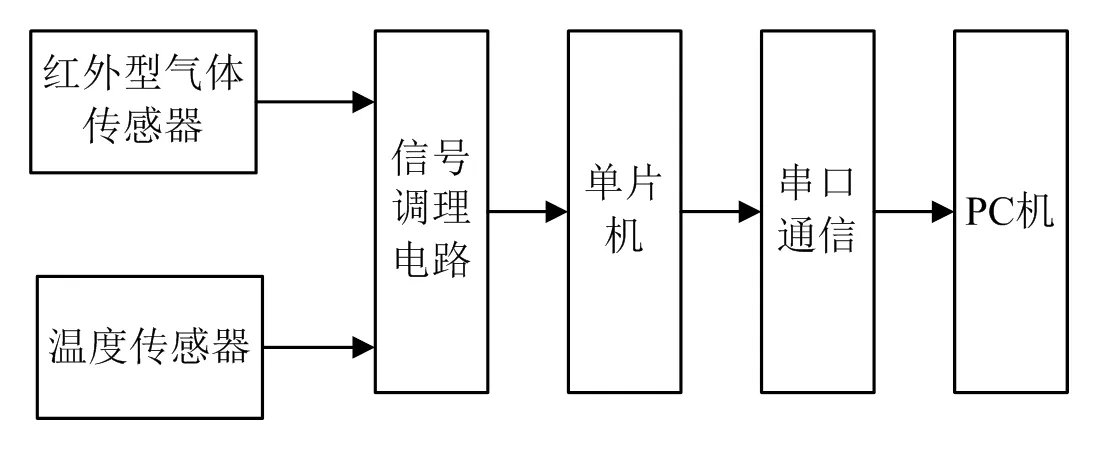
图1 系统结构

2 DLIPSO算法

2.1 动态拓扑Dbest策略

粒子的邻域拓扑结构会直接影响到粒子群的进化[5]，常见的邻域拓扑结构包括全连接Gbest策略、环形Lbest策略和分簇形Cbest策略等。上述几种拓扑策略都属于静态拓扑，由于其拓扑结构固定，不利于算法跳出局部最优[6]。而动态拓扑的结构会随着算法的进化过程而变化，可以更好地挖掘出进化不同阶段的收敛性能以适应粒子群进化过程，性能要优于静态拓扑[7]。本文提出一种改进的动态拓扑Dbest策略，如图2所示。

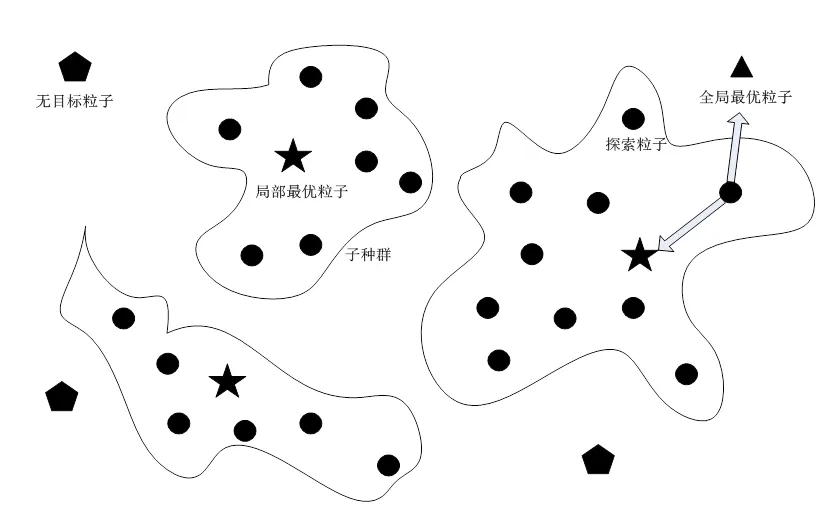
图2 改进的动态拓扑Dbest策略

在每次迭代过程中，根据各个粒子的历史最优解的优劣顺序将种群划分为全局最优粒子全局最优粒子GB、局部最优粒子LB(＝1,2,…,lb)、探索粒子EX(＝1,2,…,ex)以及无目标粒子NA(＝1,2,…,na)。全局最优粒子GB的个数为1，表示当前迭代中解最优的粒子；局部最优粒子LB的数目lb表示分簇数，它们的解较差于全局最优粒子。

探索粒子EX的个数最大，分别计算其与各个局部最优粒子的欧式距离dist,j，选择距离最短的局部最优粒子构成一簇[8]，计算公式如下：

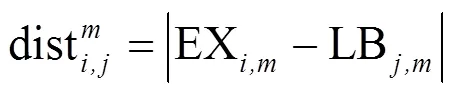
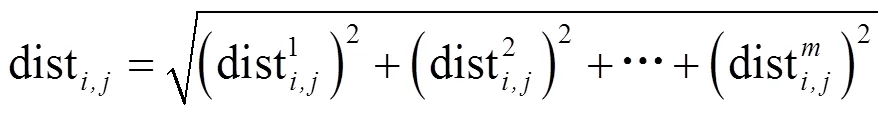
式中：＝1,2,…,ex；＝1,2,…,lb；表示粒子维数。

无目标粒子NA的解最差，在下次迭代时用于负责搜索区域内的盲点以提高粒子跳出局部极值的能力，位置更新如下式：

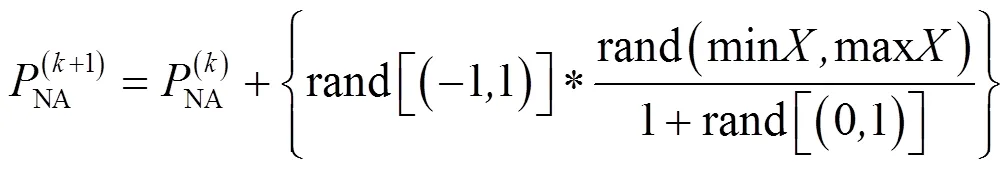
式中：NA为无目标粒子的位置；为当前迭代次数；为搜索空间；max、min分别表示搜索空间的最大值和最小值。

在每一次的循环迭代结束后，都需要根据解的优劣重新选择4类粒子，因此，4类粒子的构成并不是固定的，而是相互间可以转换的。

在第次的迭代过程中，探索粒子EX(k)会受到簇内局部最优粒子LB(k)和全局最优粒子GB(k)的共同影响，其速度和位置按下式进行更新：

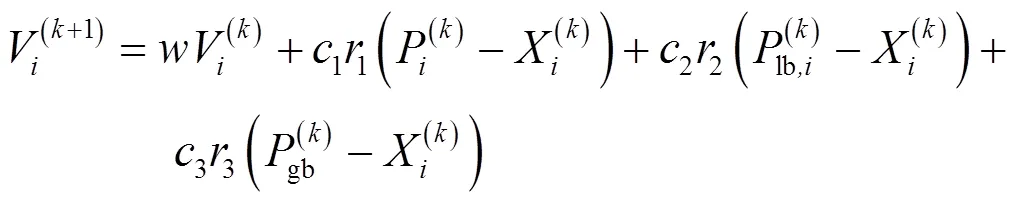
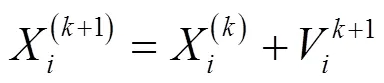
式中：P(k)表示探索粒子EX的个体极值；lb,i(k)表示局部最优粒子位置；gb(k)表示全局最优粒子位置。

2.2 DLIPSO算法介绍

提出的DLIPSO算法在粒子群进化过程中，采用改进的动态拓扑Dbest策略，能较好地适应粒子群的进化过程，有效降低粒子趋同性，在提高收敛速度的同时，有效避免算法陷入局部最优。同时，将免疫机制引入到算法中来，利用免疫系统的多样性、免疫记忆等特性增强粒子群算法的全局寻优能力[9]。在新的抗体产生过程中，引入自适应列维变异可以使整个搜索过程更加有效且稳定，平衡局部搜索和全局搜索的比例[10]。这是因为在Levy flight随机过程中，存在短距离的局部搜索与较长距离的行走，且两者相间存在，一部分解在当前最优值附近搜索，加速局部搜索；另一部分解在离当前最优值较远的空间搜索，保证算法不会陷于局部最优[11]。DLIPSO算法具体步骤如下：

步骤1：初始化有关参数及粒子群，计算每个粒子的适应度值pbestXi(＝1,…,)（为粒子数目）及全局极值gbest；根据粒子适应度值的优劣进行排序，得到全局最优粒子GB、探索粒子EX以及无目标粒子NA，并对探索粒子进行分簇，计算各簇内的局部最优粒子，建立子种群。

步骤2：判断是否达到最大迭代次数，若达到则算法结束，否则根据式(3)对无目标粒子进行更新，根据式(4)和(5)对各个子种群内的探索粒子进行更新。

步骤3：根据新的适应度值的优劣对全体粒子进行排序，得到下次迭代的4类粒子。

步骤4：将各个粒子分别与其个体极值pbest(＝1,…,)（为粒子数目）进行比较，若适应度值得到优化，则将更新后的粒子位置作为新的个体极值；将更新后的最优粒子适应度值与全局极值gbest比较，若优于gbest，则将其作为新的全局极值。

步骤5：连续迭代Limit次后，判断全局最优粒子的适应度值是否变优，若未变优，则模仿免疫调节机制，根据式(7)计算抗体（粒子）被替换的概率，否则返回到步骤3。

步骤6：若步骤5成立，则判断抗体被替换的概率是否达到替换预设值replace，若达到，根据式(9)对抗体进行自适应Levy变异；否则返回步骤3；算法持续进行，直到达到最大迭代次数。

算法初始化参数包括：学习因子1、2和3，迭代次数Max_iter，种群大小和搜索空间维数，无目标粒子数na，抗体替换概率的预设值replace，迭代限制数Limit以及惯性权重因子。

抗体变异的概率根据下式得到：

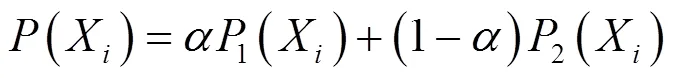
式中：是一个在[0,1]范围内的替换因子；1(X)、2(X)分别表示抗体的适应度概率、个体浓度，分别如式(7)、(8)所示：

1(X)＝pbest(－＋1)/sum(7)

2(X)＝/(8)

式中：pbestXi表示第个抗体的个体最优值；sum表示当前迭代所有抗体个体最优值的和；表示当前迭代次数；表示与第个抗体的距离小于预设值min的粒子个数。

当抗体的替换概率大于预设值replace时，采用式(9)对抗体进行Levy变异：

+1＝＋(9)

式中：X表示当前粒子的位置；X+1表示下次迭代时的粒子位置；＝[1,2,3,4]表示Levy flight的步长，如下式所得：

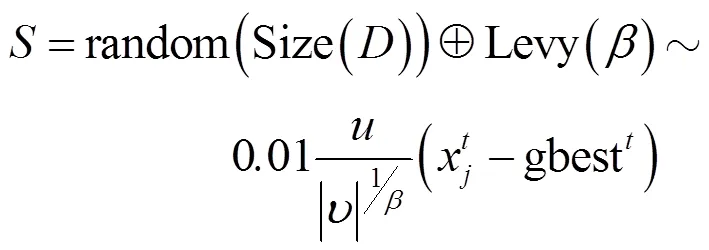
其中，和如下式所示：

～(0,2)，～(0,2) (11)

式中：

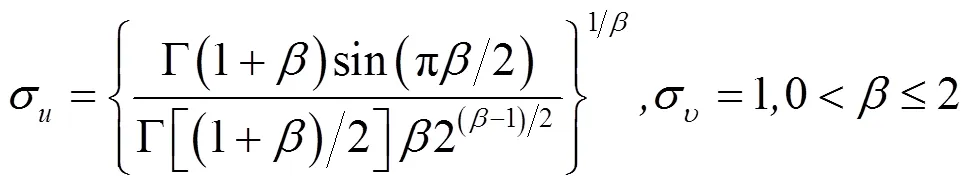
在计算变异抗体过程中，改变Levy分布的值可以获得不同的步长，这对于子代抗体的随机性是很重要的。而且当＝1时，Levy分布变为柯西分布；当＝2时，则变为高斯分布。为了更好地提高搜素能力，比较在不同分布下子代抗体的适应度值，本文算法采用的自适应Levy变异将值依次取(0,1)内的随机数、1、(1,2)内随机数以及2，即每次变异产生4个不同值的子代，比较并选择适应度值较优的后代。

3 算法性能分析及温度补偿实验

3.1 DLIPSO算法性能分析

为了观察所提出的DLIPSO算法的效果，使用5种常用基准测试函数（测试函数设定如表1所示）对标准PSO算法，现有的IPSO算法及本文提出的DLIPSO算法进行性能对比评价。算法参数设置为：学习因子1＝2＝3＝2，粒子维数＝30，种群规模NP＝150，最大迭代次数Max_iter＝1000；惯性权重因子＝0.4＋0.5(Max_iter－iter)/Max_iter，其中iter表示当前迭代次数；子种群数lb＝8，无目标粒子数na＝9，抗体替换概率的预设值replace＝0.6，迭代限制数Limit＝10，实验采用MATLAB7.0实验平台进行数值测试。表2为算法分别对每个测试函数进行50次独立试验所得收敛结果。

表1 基准测试函数设定实验数据表

从表2的数值测试结果中可以看到，DLIPSO算法搜索精度要比标准PSO算法及现有的IPSO算法更好。以测试函数Griewank为例，图3表示在该测试函数上3种算法种群最优值进化曲线的对比，横坐标表示迭代次数，纵坐标表示种群最优值取10为底的对数。从图中可以看到DLIPSO算法寻优速度快，在经过若干次迭代后，粒子仍然保持着较好的活性，能够有效地从局部极值中跳出，而另外两种算法均产生了“早熟”现象，各自陷于不同的局部极值。

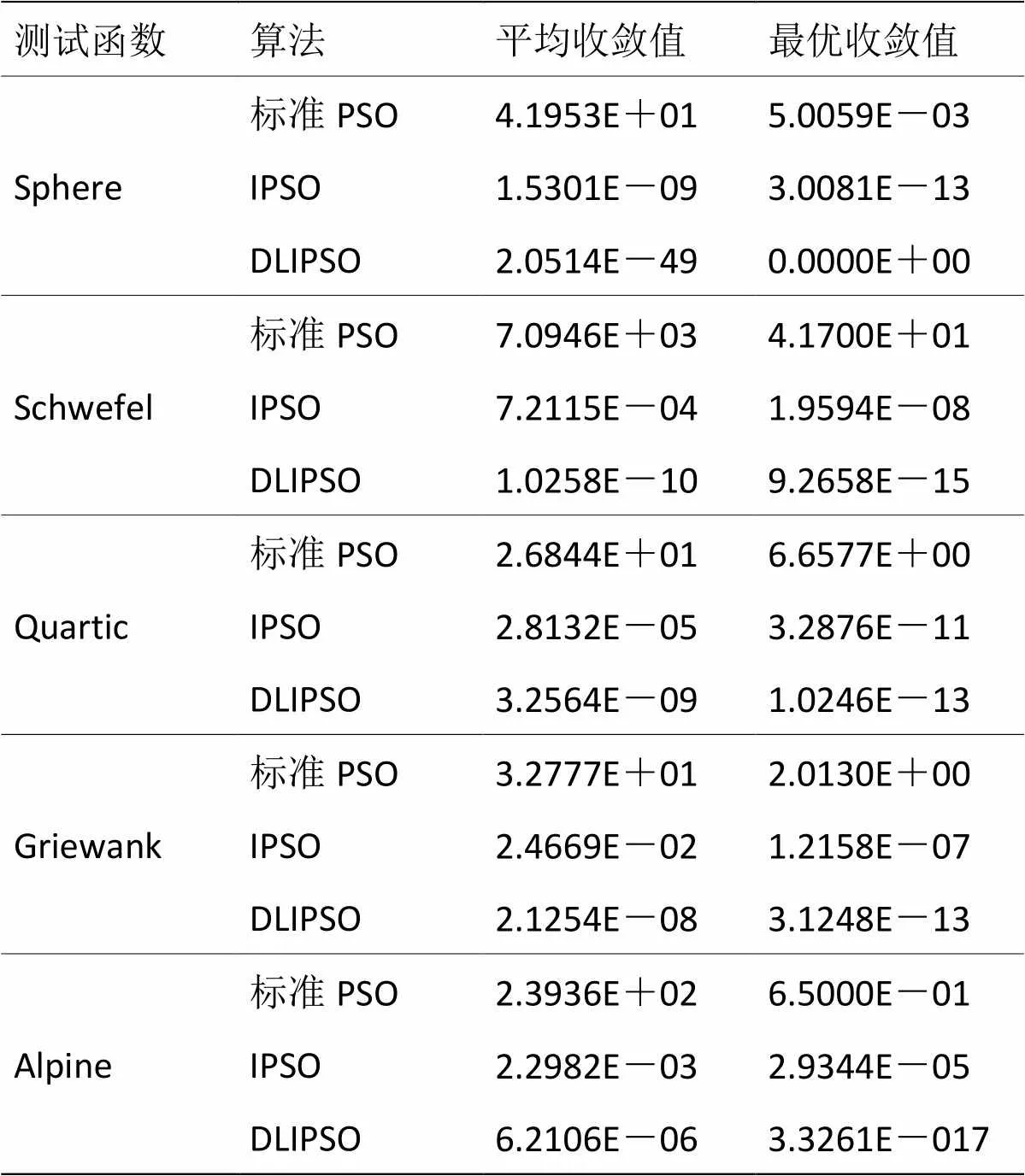
表2 数值测试结果

图3 Griewank函数寻优过程比较

3.2 温度补偿实验

红外气体传感器接触浓度为的气体后产生原始测量值0，温度传感器测量值为，两者作为DLIPSO-LSSVM模型的输入。经过训练，消除环境温度的影响后，输出修正后的预测气体浓度值*，温度补偿原理框图如图4所示。

实验选择可燃气体甲烷（CH4）作为研究对象，光源采用IRL715红外光源，探测器采用PYS3228双滤光片热释电红外气体探测器。测量滤光片的滤波参数选择3.31mm＋60mm，参考滤光片的滤波参数选择3.91mm＋90mm。首先将红外甲烷气体探测器放置在恒温箱内，环境压力控制在1atm，湿度控制在60%。对探测器通入高纯氮气，改变恒温箱内温度，探测器测试数据经过A/D转换后，通过RS232接口输出到PC端，记录测量电压、参考电压、环境温度等。然后，改变环境温度，通入不同浓度的标准气体，记录不同温度、浓度下的探测器输出信号。

图4 温度误差补偿原理框图

实验选取[－40,＋65]℃内的12个温度点，每个温度点测试20组浓度，共得到240个样本组对，选择11个温度点的样本组作为训练样本，7.5℃样本组作为测试样本。对样本及温度进行归一化处理到区间[－1,＋1]内：

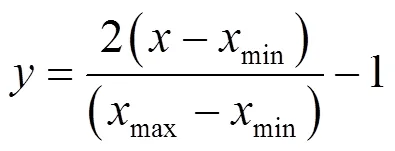
式中：、分别为样本及温度的原始数据；max、min及max、min分别为、中的最大值和最小值。

表3为部分实验原始数据，表中单位为%LEL，表示气体爆炸下限，为甲烷气体实际百分比浓度，0为测量值。实验中采用径向基（radial basis function，RBF）核函数。利用平均相对误差r定量地对比温度补偿效果，其计算公式如下：

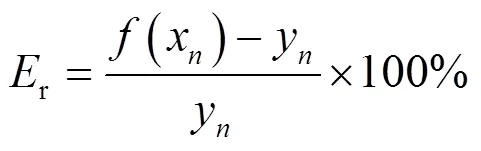
实验基本参数设置：粒子种群规模30，进化代数50，LS-SVM的正规化参数的寻优范围为1～1000，核宽度的寻优范围为0～100。首先对训练样本进行训练，然后分别对训练、测试样本进行预测，分析算法的补偿效果和泛化能力。

算法得到的最佳参数（best，best2）、训练样本均方误差、测试样本均方误差如表4中所示。

预测结果反归一化得到测试样本的预测结果如表5所示。

根据表5温度补偿结果，可知采用上述的3种温度补偿算法均起到一定的补偿作用。其中，应用DLIPSO-LSSVM预测模型进行温度补偿的相对误差最大值为4.665%，优于PSO-LSSVM（9.506%）和IPSO-LSSVM（6.194%）。可见，采用DLIPSO-LSSVM模型对气体传感器进行温度补偿可得到较为理想的补偿效果。经过多次重复实验，误差几乎都在5%范围内，表明该方法具有较强的鲁棒性。

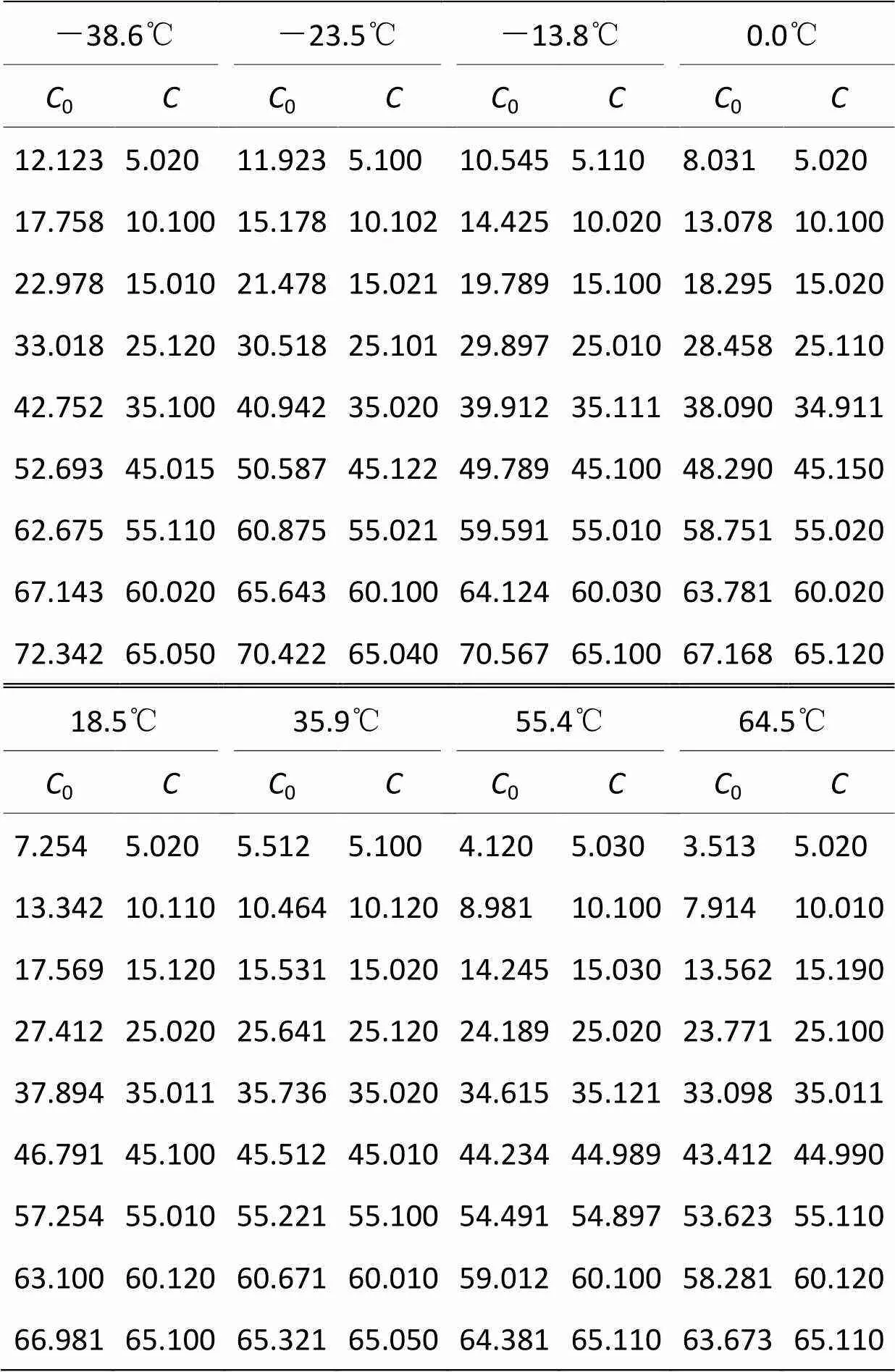
表3 部分实验原始数据

表4 参数优化结果

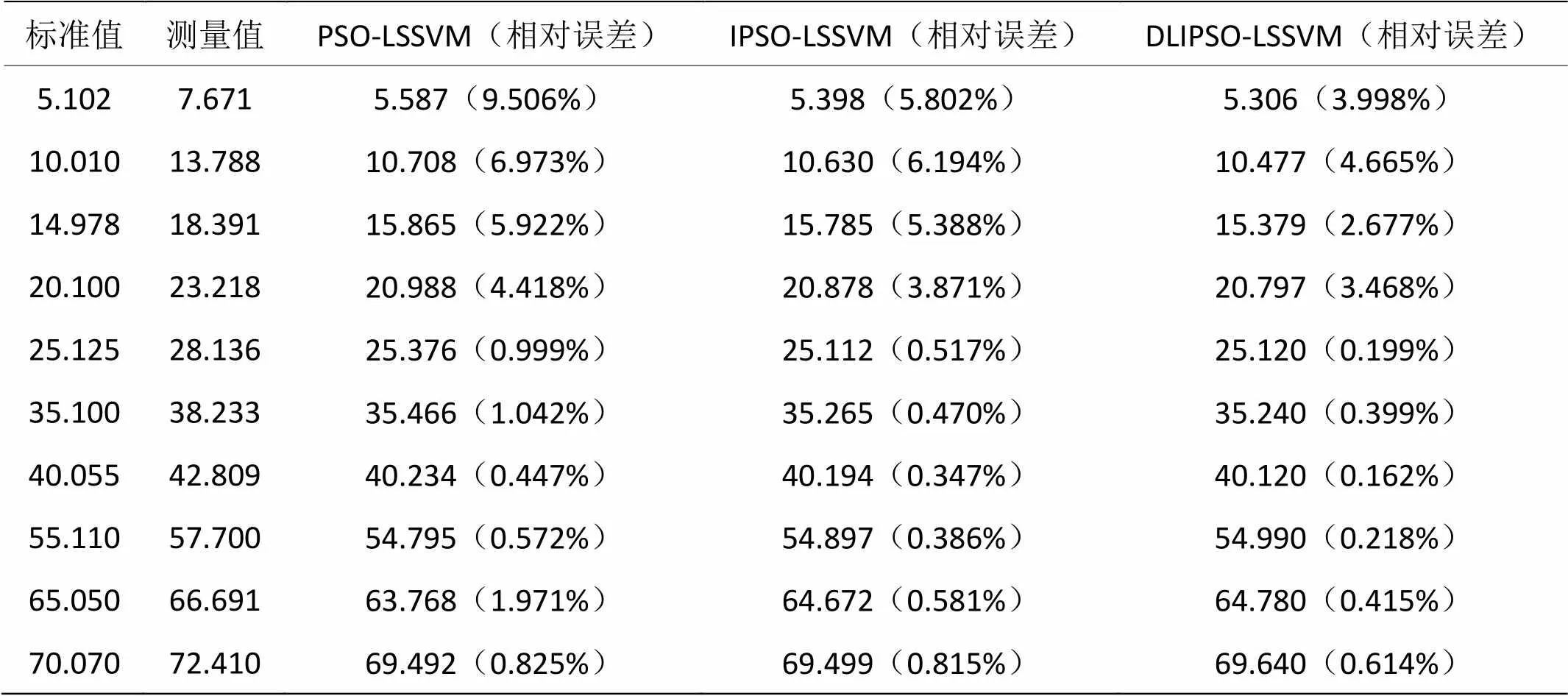
表5 7.5℃温度补偿结果

4 结论

提出了一种基于DLIPSO-LSSVM模型的红外型气体传感器温度补偿方法，算法采用改进Dbest动态拓扑策略，能较好地适应粒子群的进化过程，在提高收敛效率和避免陷入局部最优2个方面都取得了一定的提高；并在抗体变异过程中引入了自适应列维变异以提高粒子多样性。利用基准测试函数进行性能对比，数值仿真证明本算法收敛性能较标准PSO算法得到了较大提升，具有较强的抗早熟能力。实验结果表明，该模型预测精度高，通过与实测数据比较，预测结果的相对误差被控制在5%范围内。

[1] 谭秋林, 杨明亮, 熊继军, 等. 红外光学气体检测中的参数修正函数浓度计算与补偿方法[J]. 红外与激光工程, 2014, 43(5): 1396-1400.

Tan Qiu-lin, Yang Ming-liang, Xiong Ji-jun, etc. Para-meters correction function method for concentration calculation and compensation in IR optical gas measurement[J]., 2014, 43(5):1396-1400.

[2] 刘永平, 王霞, 李帅帅, 等. 基于红外技术的气体浓度检测方法研究[J]. 光子学报, 2015, 44(1): 0112002.

Liu Yong-ping. Wang Xia, Li Shuai-shuai, et al. Gas Concentration Detdction Method Based on Infrared Absorption Spectroscopy Technology[J]., 2015, 44(1):0112002.

[3] 叶玮琳, 郑传涛, 王一丁. 中红外甲烷检测仪稳定性试验及温度补偿研究[J]. 光学学报, 2014, 34(3): 0323003.

Ye Wei-lin, Zheng Chuan-tao, Wang Yi-ding. Stabilit Measurement and Temperature Compensation of Mid-Infrare-d Methane Detection Device[J]., 2014, 34(3): 0323003.

[4] 杨强大, 张卫军, 牛大鹏. 基于改进PSO的发酵过程同步串联混合建模[J]. 自动化学报, 2015, 41(3): 620-630.

Yang Qiang-da, Zhang Wei-jun, Niu Da-peng. Simultaneous Series Hybrid Modeling for Fermentation Process Based on Improved Particle Swarm Optimization[J]., 2015, 41(3): 620-630.

[5] Elliackin M N Figueiredo,Teresa B Ludermir. Investigating the use of alternative topologies on performance of the PSO-ELM[J]., 2014, 127: 4-12.

[6] Mehdi Neshat, Ghodrat Sepidnam, Mehdi Sargolzaei. Swallow swarm optimization algorithm: a new method to optimization[J]., 2013, 23(2): 429-454.

[7] Xiaolei Liang, Wenfeng Li, Yu Zhang, et al. An adaptive particle swarm optimization method based on clustering[J]., 2015, 19: 431-448.

[8] Kaveh A, Bakhshpoori T, Afshari E. An efficient hybrid particle swarm and swallow swarm optimization algorithm[J]., 2014, 143: 40-59.

[9] Ying Zhang, Yufeng Gong, Junyu Chen. Harmonic sup-pression method based on immune particle swarm optimization algorithm in micro-grid[J]., 2014, 2(4): 271-279.

[10] Ihor Lubashevsky. Equivalent continuous and discrete realizations of Levy flights: A model of one dimensional motion of an inertial particle[J]., 2013, 392(10): 2323-2346.

[11] 朱晓恩, 郝欣, 夏顺仁. 基于Levy flight的特征选择算法[J]. 浙江大学学报:工学版, 2013, 47(4): 638-643.

Zhu Xiao-en, Hao Xin, Xia Shun-ren. Feature selection algorithm based on Levy flight[J].:, 2013, 47(4): 638-643.

IR Gas Sensor Temperature Compensation Based on Improved PSO Algorithm

MAO Qibo1，YU Zhenhong1，WANG Xiangchun2

(1.,,214122,; 2.,,310000,)

Focused on the issue that the precision of infrared gas sensor is affected greatly by temperature, a new method is put forward for sensor temperature compensation based on Hybrid Immune Particle Swarm Optimization Algorithm of Dynamic Grouping with Adaptive Levy mutation-Least Square Support Vector Machine (DLIPSO-LSSVM). DLIPSO introduces dynamic topology Dbest mechanism into the PSO algorithm; the Levy mutation is introduced in the adaptive mutation of offspring in the IPSO to ensure the diversity, and opposition-based learning is used to train the offspring to improve the convergence speed. The DLIPSO algorithm is tested by benchmark test functions and the numerical experiment results show that the new algorithm has good convergence efficiency, high accuracy, strong global search ability and good stability. Based on the DLIPSO, the optimum parameter selection of Least Squares SVM(LS-SVM) is studied, and the temperature compensation model of infrared gas sensor is established. The numerical simulation results show that the relative error can be controlled within 5%.

infrared gas sensor，temperature compensation，particle swarm optimization，dynamic topology，Levy mutation，numerical simulation

TP212

A

1001-8891(2016)06-0499-06

2015-11-16；

2015-01-15.

毛琪波（1991-），男，硕士，研究领域为光谱吸收式红外甲烷气体检测研究相关方面。E-mail：15261597161@163.com。

江苏省气体传感器工程技术研究中心（BM2010645）。