基于Runge-Kutta设计运动船舶数学模型*

江衍煊　黄　焕

(1.福建船政交通职业学院　福州　350007)

(2.福建交通职业技术学院航海技术研究所　福州　350007)(3.广东海洋大学　湛江　524000)



基于Runge-Kutta设计运动船舶数学模型*

江衍煊1,2黄焕3

(1.福建船政交通职业学院福州350007)

(2.福建交通职业技术学院航海技术研究所福州350007)(3.广东海洋大学湛江524000)

摘要为便于将海上船舶避碰问题利用计算机进行研究,需要把船舶的运动特点用数字形式进行模拟,把风、流和浪等问题一起讨论并寻找最合适的数学表达式模拟出船舶航行的状态,这样才便于研究海上船舶避碰的问题。现以六面体船舶为典型特征来进行研究,叠加了矢量风、流和浪的数学表达式,并利用高阶Runge-Kutta推导微分方程进行高精度仿真船舶海上航行的特征,并建立相应的数学模型以便于讨论船舶避碰问题。

关键词建模; 仿真; 六面体; 算法

Movement Ship Model Design Based on Ronge-kutta

JIANG Yanxuan1,2HUANG Huan3

(1. Fujian Chuanzheng Communications College, Fuzhou350007)

(2. Navigation Technology Research Institution, Fujian Chuangzheng Communications College, Fuzhou350007)

(3. Guangdong Ocean University, Zhanjiang524000)

AbstractIn order to facilitate the research for preventing collsions at sea, it can be studied via computers, which involves digital simulation of ship motion characteristics, considerations of wind, current and waves, as well as the layout of the most appropriate mathematical expressions to simulate the ship moving state. Based on the typical features of hexahedral ship, this paper researches superposing vector wind, current and waves, precisely simulating the characteristics of ship’s navigation at sea by high-order Runge-Kutta differential equation, establishing corresponding mathematical model, studies the prevention of ships’s collisions at sea.

Key Wordsmodeling, simulation, hexahedron, algorithm

Class NumberTP391.9

1引言

为了能够利用计算机仿真船舶的航行状态,在考虑到船舶在水中的运动会受到多方面的影响下,目前把船体的运动状态和受力考虑成六面体进行研究[1],研究船舶所受到周围各种作用的影响而建立相应的数学模型并用微分方程表示。

2影响船体运动的因素

2.1水的作用

船舶航行会受到空气和水的作用,水面下存在水的阻碍作用,主要由基本阻力、摩擦阻力以及兴波阻力组成。基本阻力是静水时对运动船体所产生的阻碍作用,摩擦阻力是船体对水运动时,水的粘性所产生的阻力。兴波阻力是船舶对水运动时产生船舶兴波,该兴波将沿着船体周围所导致受到的压力发生了变化而产生的阻碍作用。若船舶首尾线与流向存在交角时,流速和静水船速的合成速度将使船舶向水流来向相反一舷运动的效果[3]。

2.2风的作用

船舶在航时水面以上部分将所受到风的影响,若顶风船舶就会减速,反之若顺风则船速会减速;风向与首尾面斜交或者垂直则船舶受到风的影响会朝着下风漂移,船舶受到影响后船首将向上风或下风偏转[11]。

3船舶数学建模

3.1模型的选取

研究船舶运动的核心内容是为了船舶避碰,建立船舶的数学模型就是把复杂的船舶运动用数学公式进行近似和简化表达,但也不能太过于简单导致无法充分描述系统的主要性能,所以建立数学模型要尽量降低复杂度,同时尽可能提高精度。模型的设计必须包括风、浪、流的干扰,且带有非线性的船舶数学模型,才能比较真实地模拟出船舶运动的实际状况[1]。

设船舶的位置[x0y0]T引入六自由度的简洁线性数学模型方程,则其状态变量为:x(6)=[vrΔφδx0y0],速度平衡方程:

(1)

其中r为预设航向,Δφ为航向偏差,δ为输入舵角。因风浪对船舶漂移速度v及船首转向角速度r影响以及海浪对船舶位置的改变,若流为恒速,那就会直接影响船舶位置和速度的变化,而不会影响航向,得到的速度平衡方程为[1]

其中:Vc为流速度,γc为流向。

3.2流的影响

用Norrbin简洁的非线性表达非线性力、力矩的流体动力表达式[2]:

其中,

式中C为横流系数,在自动舵控制的闭环系统研究中应用数学模型取值0.3～0.8之间。

3.3风力的干扰

式中Cγ(γR)、CN(γR)为风力和风力矩系数,经计算得出风力系数如表1所示。

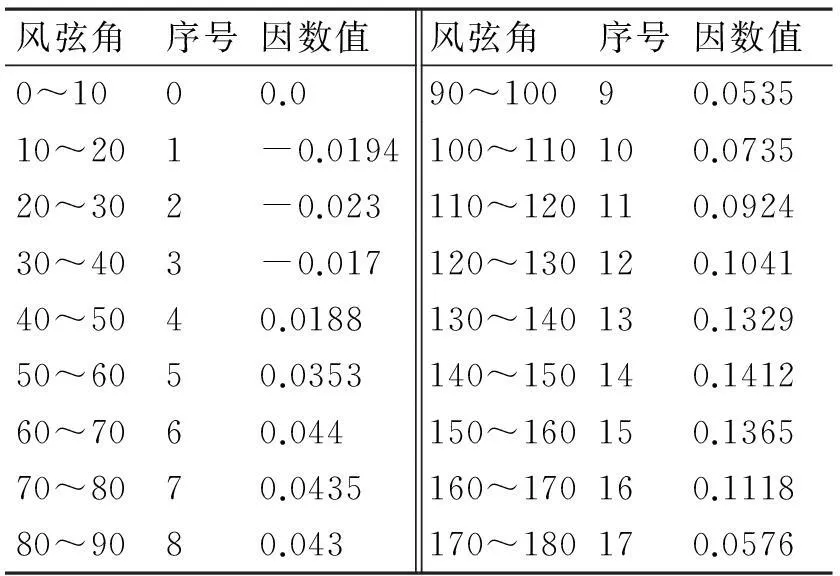
表1　风力系数表(wind coefficient)

通过插值法查表求得CN(γR)的值,n为表中序号,由式n=floor(γR/10)进行浮点数取整获得当前数的最大整数。ρA为空气密度值,C为表中n对应的风力系数值,AL是人工输入的船舶水线面上侧投影面积,或者由船舶尺寸参数进行估算,VR为相对风速,VT为绝对风速,γR为风弦角。同样通过插值法查表可求得CN(γR)的值。

uR=-VTcos(αWIND-φ)-u

vR=-VTsin(αWIND-φ)-v

其中αWIND,ψ变动范围为0～360°,γR变动范围为0～±180°,风向相对从右舷来时γR>0。大气湍流形成的脉动风可以看作类似白噪声的形式,则该标准差与VT的平方成正比,如下式[6]:

3.4波浪的影响

任何一短时刻的波浪可以看成固定频率、周期和波高的规则波,假设船舶是规则的六面体,得到波浪的计算式:

其中k代表波浪数,T为周期,L为波长,ξ(t)表示波浪在坐标系原点处的振荡,s(t)为波浪面在原点出的斜率,这里的ξ是沿着波浪传播的方向。

4仿真算法

研究船舶自动避碰不仅需要研究避碰算法还需要研究船舶航行的数学模型,只有数学模型与船舶实际在航相一致才能充分利用计算机进行仿真,以便研究船舶的避碰。将船舶运动的数学模型转换成计算机编程模块,所以在进行编程之前必须将其数字化、离散化。在考虑编程之前,必须选择合理恰当,并且算法简单,最重要的是精度要高的策略[6]。

4.1船舶拟人智能避碰决策(PIDVCA)

PIDVCA是进行自动推理、定量计算、分析,避碰决策的智能化很强,对复杂海况的避碰时增加了大量的选择性,导致在决策查找能力方面必然需要处理巨大数据量,因此对计算机数据处理速度要求很高,这就降低避碰决策的时效性,导致对物标判断延误造成决策失误而带来安全隐患。

4.2粒子群优化算法(PSO)

PSO源于人工生命和进化计算理论,算法用的参数较少、简便易行、较快的收敛速度等优点,但是这种算法搜索精度低,收敛速度慢,时效差。

4.3神经网络避碰决策模型。

神经网络是通过学习专家的知识和经验和调用网络结点的权系数,并利用数据库中的专家推理机制,从而实现自动避碰决策过程,这种算法需要大数据的专家推理进行计算,时效性也比较低。

在避碰决策时必须有其无可替代的数学公式的准确性,然而实际航海环境中不仅需要算法的数学准确性更需要结合实际航海规则。不仅需要研究避碰算法还需要研究船舶航行的数学模型,只有数学模型与实际在航相一致才能充分利用计算机进行仿真[7]。

4.4Runge-Kutta算法

为了尽可能模拟船舶的运动状态,考虑用龙格-库塔方法进行跟踪船舶运动,再运用计算机进行仿真,只要龙格-库塔的阶数足够高,就可以最大限度地模拟出船舶的运动态势。

龙格-库塔(Runge-Kutta)方法简称R-K法,它是应用于高精度单步跟踪的一种算法。利用该算法时步长不能太大,否则会导致精度下降。单阶的R-K公式的稳定性和跟踪的精度远不如高阶的R-K公式,所以为了高精度跟踪船舶的运动状态需要实时的最优三级二阶R-K公式或四级三阶R-K公式。获取Runge-Kutta高阶的方法:

例如,某函数y(x)在xi-1处的斜率作为y(x)在[xi-1,xi]上的平均斜率K即:

K=y′(xi-1)=f[xi-1,y(xi-1)]≈f(xi-1,yi-1)

此为一阶Runge-Kutta式。函数式为:yi=yi-1+hf(xi-1,yi-1)。

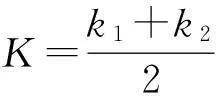
为了让仿真的计算表达与真实运动的误差尽量小,应该使用高阶Runge-Kutta方法,利用类似插值原理,在相应的区间多取几个点,取相应点斜率的加权平均值作为平均斜率。构造3阶或4阶的R-K推断公式就为了获取更高精度。四阶的公式为

为了提高精度的要求下,采用非线性数学模型,其离散化方法采用数值积分法,并采用四阶的RUNGE-KUTTA方法建立的数值仿真模型。利用上式进行推算得到船舶数学模型的四阶表达式:

对于类似这种迭代方式的表达式,比较适合使用游标进行计算机计算。

begin

temp:=q;

q:=p;

p:=SPACE[q].next;

SPACE[Q].next:=temp;

Return()

End

利用相关计算机语言编程进行迭代之后计算得到相关数值如表2所示。

表2　计算出的相关数值

5数据模型表示

有了以上的表达式与计算机程序的计算结果之后,在设计船舶仿真时就需要添加对应的风流浪以及舵的作用,才能完整地体现出船舶运动状态。

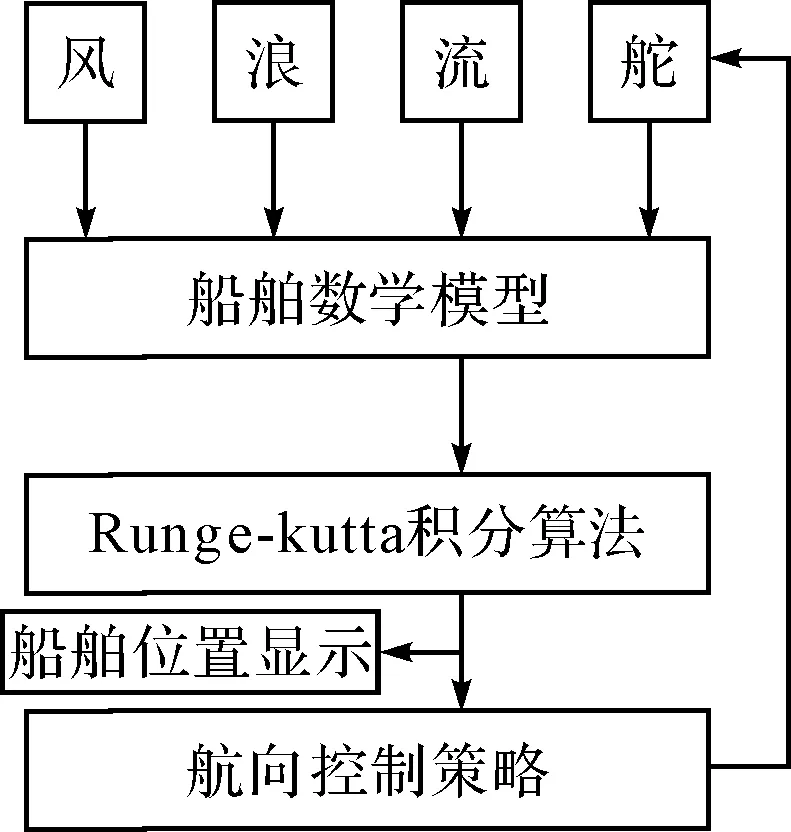
图1　船舶运动参数叠加后情况

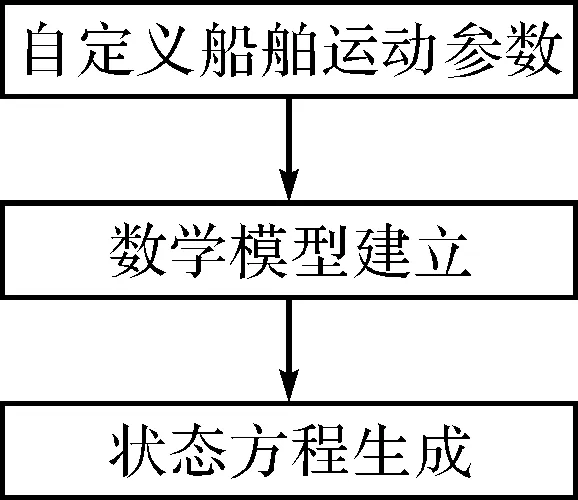
图2　状态方程设置

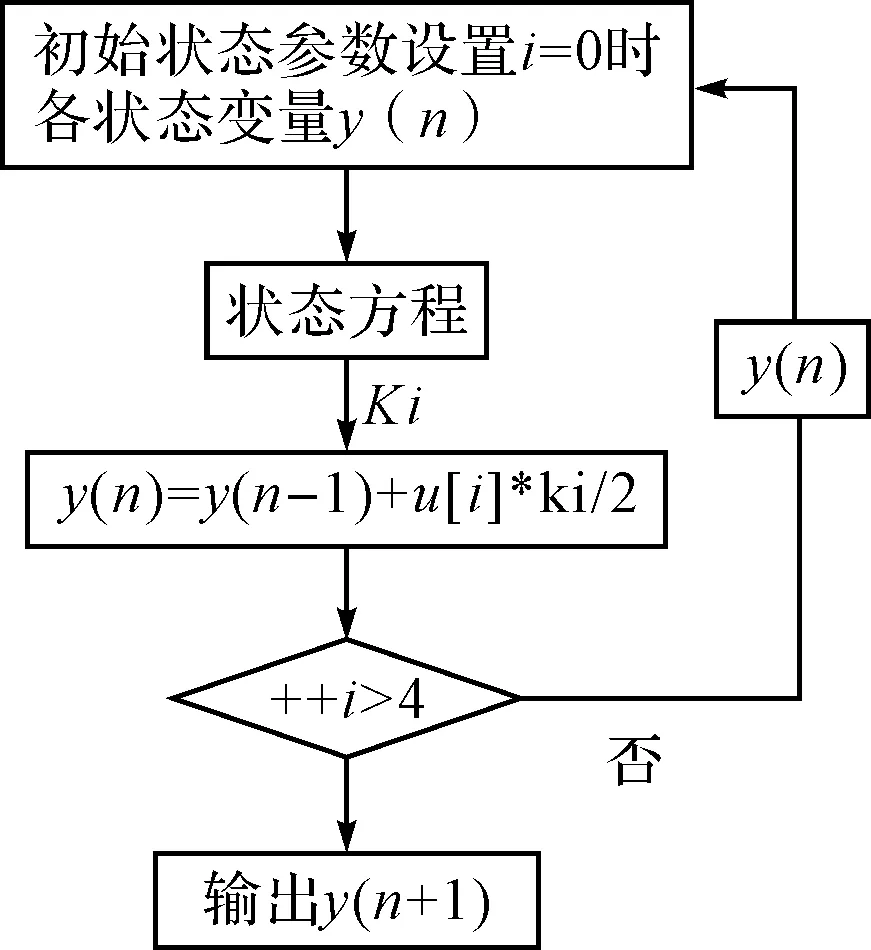
图3　船舶模型的特征性

其中yn代表六自由度船舶模型中状态初始量,yn+1代表仿真中期望得到的离散化结果,函数代表由数学建模之后由状态空间模型方程计算出的微分方程,就是把船舶建模与Runge-kutta之间建立了联系。如图2所述在船舶部分初始化条件设置之后,就可以显示出航向与位置,这样船舶的运动状态就基本可以确定了。

设计选取六自由度的船舶模型,考虑风、浪以及流对船舶的影响为依据对船舶模型进行了推导,利用四阶R-K方程可以高精度地接近船舶运动状态的特点。

6结语

利用龙格-库塔算法进行仿真,在数学计算中误差最小,利用计算机进行仿真时计算量不大,速度比较快。这种模型在船舶仿真过程中,对于涉及多艘船舶互见的运动态势,该方法在船舶间能够更精确计算出相关的避碰数据,有利于船舶及早采取行动。

参 考 文 献

[1] 孙宏放.船舶三自由度仿真平台设计与预报方法研究[D].哈尔滨:哈尔滨工程大学硕士论文,2006:46-126.

[2] 王凤军.船舶避碰仿真平台设计[D].大连:大连海事大学,2013:66-89.

[3] 叶松,等.海浪干扰对船舶航向影响规律研究[J].舰船电子工程,2015(1):65-67.

[4] 史建,秀.船舶横摇运动智能控制及其虚拟现实仿真研究[D].大连:大连海事大学硕士论文,2010:42-48.

[5] 汪宏,等.船舶失控撞击高桩码头结构的数值仿真分析[J].水运工程,2015(6):51-55.

[6] 田超.风浪流作用下船舶操纵运动的仿真计算[D].武汉:武汉理工大学硕士论文,2003:66-87.

[7] 吴立金,等.面向船舶软件的仿真测试平台研究[J].计算机测量与控制,2015(5):1451-1456.

[8] 邢道奇,龚铭.船舶航向模糊自适应云模型控制[J].船舶,2015(3):42-47.

[9] 蔡新梅.基于UWB技术的船舶避碰系统抗干扰研究[J].舰船电子工程,2015(1):68-70.

[10] 殷虎,陈瑜.虚拟技术在船舶系统设计中的应用研究[J].装备制造技术,2015(1):228-229.

[11] 田德,等.风能与动力工程专业教学理念研究与实践[J].风能,2015(1):44-45.

中图分类号TP391.9

DOI:10.3969/j.issn.1672-9730.2016.02.023

作者简介:江衍煊,男,硕士,副教授,研究方向:船舶通信导航与自动化。黄焕,男,硕士,讲师,研究方向:船舶通信导航及计算机在航海中的应用。

基金项目:福建省教育厅科技项目(编号:JB08275,JB10226)资助。

*收稿日期:2015年8月14日,修回日期:2015年9月30日