大气环境中PM2.5在线监测及评价理论研究*
王玉田 张亚吉 苑媛媛 赵 煦 牛凯增
(燕山大学河北省仪器科学与技术重点实验室,河北 秦皇岛 066004)
大气环境中PM2.5在线监测及评价理论研究*
王玉田 张亚吉#苑媛媛 赵 煦 牛凯增
(燕山大学河北省仪器科学与技术重点实验室,河北 秦皇岛 066004)
基于光散射法研制了一种PM2.5在线监测系统,运用该系统对PM2.5质量浓度进行实时监测。鉴于PM2.5在空气质量评价中仅作为一个参考指标,专门针对PM2.5的评价机制研究较少,将层次分析法与模糊评价法相结合,对一段时间内PM2.5的浓度进行评价,得到时段内空气PM2.5的质量状况。模糊评价法可很好地反映评价等级划分的模糊性和连续性,层次分析法能够将复杂的系统进行定量处理,评价结果符合实际情况。
PM2.5测量 空气质量评价 光散射 层次分析 模糊评价
PM2.5是指空气动力学当量直径小于或等于2.5 μm的颗粒,为可吸入颗粒物。PM2.5的化学成分主要包括有机质、可溶性物质和微量元素等。由于PM2.5粒径较小,被吸入人体后可直接进入肺泡沉积,导致心与肺的相关疾病,PM2.5还会破坏染色体和DNA结构导致基因突变。PM2.5的来源主要包括自然源和人为排放,其中人为排放是PM2.5的主要来源[1-4]。
PM2.5作为重要的空气质量参考指标,在地区环境空气质量信息中经常实时发布。空气质量指数法是评价区域环境空气质量的常用方法,该方法计算简单,发布效率高,可以实现对空气质量的实时监控。值得注意的是,在进行空气质量指数评价时参考的是PM2.5、PM10、CO、SO2、NO2和O3的平均质量浓度,而PM2.5在多个地区已经成为大气环境污染的首要污染物,仅将其作为一个参考指标评价空气质量已不满足人们对PM2.5污染的了解需求。
我国对于PM2.5的监测研究正处于起步阶段,没有足量的实测数据和完整的科学理论。本研究构建一套PM2.5在线监测系统可以实现对PM2.5的实时监测,并将模糊评价法和层次分析法相结合对PM2.5浓度进行评价,得到PM2.5的污染状况,为PM2.5污染水平的研究提供更多依据。
1 基于光散射法的在线监测系统
1.1 光散射法
测量空气中污染物浓度的方法可分为采样法和非采样法,采样法包括微量振荡天平法、滤膜称重法、β射线吸收法,非采样方法包括黑度法、光散射法。光散射法在烟雾粉尘测量中具有测量时间短、测量精度高等特点[5]。光照射到空气中的悬浮颗粒上发生散射,其当颗粒物的性质保持不变时,自身的质量浓度和散射光强度成正比关系,利用转换系数即可得到颗粒物的质量浓度。光散射法结合了颗粒物相关参数和Mie散射理论,反推出颗粒物的质量浓度,单个颗粒物的散射光强表达如式(1)所示。
(1)
式中:IS(θ)为单个颗粒物在θ方向的散射光强,cd;θ为散射角;d为颗粒物直径,μm;λ为入射光波长,μm;m为折射率;I为入射光强,cd。
当有N个颗粒物时,散射光强表达如式(3)所示。
(2)
(3)
式中:W为颗粒物质量浓度,μg/m3;ρ为颗粒物密度,mg/m3。
在固定测试装备中,入射光强I、入射光波长λ、颗粒物直径d、密度ρ、折射率m、散射角θ均视为定值,则可得散射光强与颗粒物质量浓度的关系。该方法可实现PM2.5的实时在线非接触监测,直接得到测量数据。
1.2 测量原理
目前国内外还未研制出专门测量PM2.5质量浓度的传感器,只能将测量小颗粒物的粉尘传感器近似看作测量PM2.5的敏感元件。敏感元件要具备灵敏度高、稳定性可靠等特点,最终选择GP2Y1010AU0F粉尘传感器为敏感原件,其可测量0.8 μm以上的微小粒子,具有极低的电流消耗(最大20 mA,典型11 mA),敏感元件的工作原理如图1所示。发光二极管(LED)发出的光照射到细颗粒物后发生散射,光学接收器(PD)接收散射光,把光脉冲转换成电脉冲,在颗粒物性质保持一定的前提下,经过电路的放大、识别,利用颗粒物光强与质量浓度的转换关系就可得到颗粒物浓度。
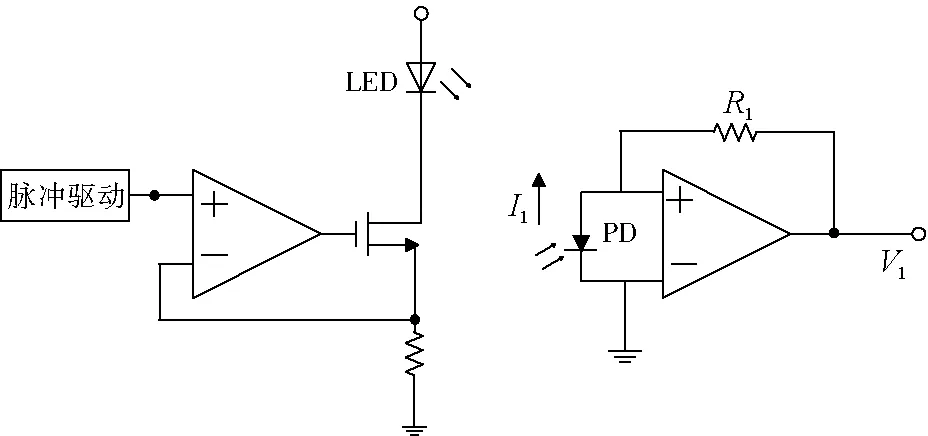
图1 敏感元件工作原理Fig.1 Operating principle of sensor
根据图1有:
V1=I1R1
(4)
式中:V1为输出电压,V;I1为流经PD的电流,A;R1为电阻,Ω。
脉冲驱动控制LED发出光强,PD将接收到的光信号转换为电信号,流过PD的电流与散射光强呈线性关系,如式(5)所示。
I1=kI(θ)
(5)
式中:k为直线斜率。
敏感元件中LED的驱动周期为10 ms,脉冲宽度为0.32 ms,取样时间为0.28 ms。结合式(3)、式(4)、式(5)即可得到输出电压V1与颗粒物质量浓度W的关系。将该设备放在不同粉尘情况的场所中,记录V1与W的数据,绘制两者关系曲线,如图2所示。

图2 颗粒物质量浓度与输出电压的关系Fig.2 Relationship between particulates concentration and the output voltage
由图2可见,当颗粒物质量浓度在500 μg/m3以内时,V1与W基本呈线性相关,关系式见式(6),因此可根据LED输出电压反推出颗粒物质量浓度。
W=(0.17×V1-0.1)×1 000
(6)
PM2.5监测系统的核心为敏感元件,在当前PM2.5监测领域,部分PM2.5监测仪采用激光粉尘传感器,激光粉尘传感器和红外粉尘传感器的测量精度相差不大,激光粉尘传感器的光源为激光LED,因此结构和电路复杂,价格较高;红外原理的粉尘传感器技术较成熟,光源为红外LED光源,结构和电路相对简单,价格合理,更具有发展潜力。
2 模糊层次分析法
2.1 层次分析法
模糊层次分析法是将层次分析法和模糊评价法相结合,采用层次分析法来确定评价指标体系中各个指标的权重值,使用模糊评价法对涉及的模糊指标进行评定[6-7]。层次分析法确定权重系数有以下4个步骤:
(1) 建立递阶层次模型
一个有层次的结构模型需要3个层次:最高层、中间层(准则层)、最底层(方案层)。建立各层次的因素集U,令U=(U1,U2,…,Un)。
(2) 构造判断矩阵
判断矩阵中元素的取值一般选用1~9标度法,标度取值及定义如表1所示。根据表1中判断矩阵标度定义,对评估因素集中的因素进行两两比较,构造n阶判断矩阵P[8-9]。

表1 判断矩阵标度取值及定义1)
注:1)与其他因素相比,其他因素更重要时,标度取值根据重要程度取相应倒数。
(3) 确定权重
采用层次分析法确定权重系数,本质上是计算判断矩阵的特征向量和最大特征值。首先,计算判断矩阵P中第i行各元素的乘积Mi;其次,计算Mi的n次方根得Wi,则向量W=[W1,W2,…,Wn]T归一化处理即为所求特征向量,即判断矩阵中各元素的权重;最后,计算判断矩阵P的最大特征值[10],各参数计算公式如下:
(7)
(8)
(9)
式中:(PW)i为向量PW中的第i个元素。
(4) 一致性检验
为提高权重评价的可靠性,必须对判断矩阵作一致性检验,故引入一致性指标CI。
CI=(λmax-n)/n-1
(10)
多阶判断矩阵还需引入平均随机一致性指标RI,RI值的确定如表2所示。
一致性比率CR计算如下:
CR=CI/RI
(11)
当CR<0.10时,认为判断矩阵具有满意的一致性,否则需要调整[11]。
2.2 模糊评价法
由于本研究是对一个采样点一段时间内的PM2.5进行评价,故采用一级模糊评价分析方法。一级模糊评价步骤如下:
(1) 建立因子集
因子集是综合评价中各评价因素所组成的集合,一级模糊评价中并不涉及其他指标层,在对一个时间段内多个时刻的PM2.5浓度进行评价时,因子集就是参与评价的各个时刻PM2.5浓度。一般设因子集为Z,Z=(z1,z2,…,zn)。计算中还需确定因子集中各因子的权重,设各因子权重向量为A,A=(a1,a2,…,an),其中:
(12)
(2) 建立评价集
评价等级是用来评价各个因素的模糊概念,评价等级个数通常不超过9而大于4,且取奇数的情况较多。设有x个评价等级,评价集一般表示为V=(v1,v2,…,vx)。
(3) 确定单因素评价矩阵
对因子集中的某个单因素作单因素评价,一般采用专家调查法对各指标进行评分,根据评分结果构建模糊关系矩阵R(见式(13)),rij计算方法见式(14):
(13)
rij=yij/y
(14)
式中:y为专家的总人数;yij为y个专家中选择zi隶属于vj的人数。
(4) 确定模糊子集B
当因子权重向量A和单因素评价矩阵R已知时,对R作模糊线性变换,可把A变成评价集V上的模糊子集B。
B=A*R=(b1,b2,…,bx)
(15)
式中:*为广义模糊合成运算符号。

表2 判断矩阵的RI值
2.3 最大隶属度原则

(16)
(17)



表3 最大隶属度原则的有效性判断
3 实验部分
3.1 监测数据的获取
利用前文构建的PM2.5监测系统测定PM2.5实时浓度,选定某市上午10:00—11:00时段,每隔10 min记录1次,每个时间点读取5个数据,监测结果如表4所示。
3.2 监测数据的评价
由层次分析法的相关概念,以表4中不同时刻的平均值建立因素集,根据表1中判断矩阵的标度及其定义,对各时刻浓度相对重要性进行主观比较,得到判断矩阵P(见式(18)),由式(7)、式(8)计算得到权重计算的相关参数,结果如表5所示。

(18)
根据表2确定的RI值,由式(9)、式(10)、式(11)可得一致性检验计算结果,如表6所示。由表6可见,判断矩阵一致性比率CR<0.10,具有满意的一致性,无需调整。
利用模糊评价法确定多个时间点监测数据的浓度指标。首先,确定准则层因素集Z,Z中的因子为监测期间各时间点PM2.5质量浓度平均值,则Z=(57.80,57.78,57.78,57.76,57.76,57.74,57.70);由式(12)计算得到Z中各因子的权重A=(0.069,0.129,0.069,0.346,0.129,0.129,0.129)。其次,确定评价集。本研究设置评价等级数为5,即评价集V=(v1,v2,v3,v4,v5),对应的评价等级评分标准分别为优(v1),良(v2),轻度污染(v3),重度污染(v4),严重污染(v5)。

表4 监测数据

表5 多时间点权重计算相关参数

表6 一致性检验实验结果
利用专家调查法,根据已设定的评价集,请20名专家对各个时刻的空气质量进行评分,则y值为20,记录各时刻选择zi隶属于vj的专家人数,由式(14)可得到指标层的单因素评价矩阵R。

(19)
在模糊评价综合算法中选用(·,+)模型,则B=A*R=(0.41,0.59,0,0,0),B中最大元素为b2,值为0.59。根据最大隶属度原则,评价结果属于v2等级,即为良。
3.3 评价结果检验与分析
对最大隶属度原则进行有效性判断,计算最大隶属度原则的改进判断方法,根据式(16)、(17)计算判断结果有效性,如表7所示。

表7 有效性计算结果
由于α=0.595,根据表3可知计算结果比较有效,不需要再进行调整。
实验结果表明,该市当天10:00—11:00的时间段内,PM2.5污染状况为良。该方法考虑了污染等级划分的模糊性,可应用于任意时间段内空气PM2.5的质量评价,评价结果符合实际情况,实用性强。
4 结 语
(1) 研究了大气环境中PM2.5在线监测系统与评价理论,能够实现对PM2.5质量浓度的实时测量和对测量结果的综合评价,确定其空气状况。
(2) 在PM2.5的评价中,层次分析法能将复杂的系统分解,将思维过程数学化、系统化,模糊评价法充分考虑到污染程度等级划分的模糊性,将层次分析法与模糊评价法相结合,采用模糊层次分析法对PM2.5浓度进行评价,更符合实际。
(3) 以某市10:00—11:00时段PM2.5实时监测数据为例,运用所提出的评价方法对空气PM2.5的质量进行综合评价,对评价结果进行分析和总结,最后得到该环境中PM2.5的评价结果为良。
参考文献:
[1] HUANG Guanghan,CHENG Tiantao,ZHANG Renjian,et al.Optical properties and chemical composition of PM2.5in Shanghai in the spring of 2012[J].Particuology,2014,13(2):52-59.
[2] DU Xuan,KONG Qian,GE Weihua,et al.Characterization of personal exposure concentration of fine particles for adults and children exposed to high ambient concentrations in Beijing,China[J].Journal of Environmental Sciences,2010,22(11):1757-1764.
[3] PUI D Y H,CHEN S C,ZUO Zhili.PM2.5in China: measurements,sources,visibility and health effects,and mitigation[J].Particuology,2014,13(2):1-26.
[4] 李润奎,李志鹏,高文举,等.北京市大气PM2.5的季节特征和空间趋势[J].中国科学通报,2015(3):387-395.
[5] 徐庆君,韦德泉,田贵才.基于Mie散射理论的铌酸锂晶粒散射特性[J].发光学报,2009,30(6):867-871.
[6] GORAI A K,KANCHAN,UPADHYAY A,et al.Design of fuzzy synthetic evaluation model for air quality assessment[J].Environment Systems and Decisions,2014,34(3):456-469.
[7] 郭金玉,张忠彬,孙庆云.层次分析法的研究应用[J].中国安全科学学报,2008,18(5):148-153.
[8] MANDIC K,DELIBASIC B,KNEZEVIC S,et al.Analysis of the financial parameters of Serbian banks through the application of the fuzzy AHP and TOPSIS methods[J].Economic Modelling,2014,43(2):30-37.
[9] ZAFARANI H R,HASSANI A,BAGHERPOUR E.Achieving a desirable combination of strength and workability in Al/SiC composites by AHP selection method[J].Journal of Alloys & Compounds,2014,589(4):295-300.
[10] 邓雪,李家铭,曾浩健,等.层次分析法权重计算分析及其应用研究[J].数学的实践与认识,2012,42(7):93-100.
[11] LI Dongsheng,YANG Qiulin,YU Deqiang.On enterprise social responsibility comprehensive evaluation based on two-step fuzzy evaluation method[J].Modern Economy,2013,4(1):66-72.
[12] JIA Junsong,FAN Ying,GUO Xiaodan.The low carbon development (LCD) levels’ evaluation of the world’s 47 countries (areas) by combining the FAHP with the TOPSIS method[J].Expert Systems with Applications,2012,39(7):6628-6640.
[13] ZHAO Xiongfei,LIU Yongbao,HE Xing.Fault diagnosis of gas turbine based on fuzzy matrix and the principle of maximum membership degree[J].Energy Procedia,2012,16:1448-1454.
StudyonatmospherePM2.5onlinemonitoringandevaluationtheory
WANGYutian,ZHANGYaji,YUANYuanyuan,ZHAOXu,NIUKaizeng.
(MeasurementTechnologyandInstrumentKeyLabofHebeiProvince,YanshanUniversity,QinhuangdaoHebei066004)
Based on light scattering method,a PM2.5online monitoring system was established. The system was applied to monitor PM2.5concentration in real-time. Considering PM2.5was only a reference indicator in the air quality index method,and few studies devoted to PM2.5evaluation mechanisms,this paper proposed fuzzy analytic hierarchy process,which combined fuzzy evaluation method with analytic hierarchy process,to evaluate PM2.5concentrations in a period of time. Fuzzy evaluation method could reflect the fuzziness and continuity between the evaluation level,and analytic hierarchy process could deal with complex systems quantitatively. The case analysis showed that the evaluation results of fuzzy analytic hierarchy process accords with actual conditions
PM2.5measurement; air quality evalution; light scattering; analytic hierarchy; fuzzy evaluation
王玉田,男,1952年生,博士,教授,主要从事光电子学与激光技术研究。#
。
*国家自然科学基金资助项目(No.61471312);河北省自然科学基金资助项目(No.F2015203240)。
10.15985/j.cnki.1001-3865.2016.12.001
编辑:丁 怀 (
2016-06-20)

