Analysis of Metamaterial Cloaks Using Circular Split Ring Resonator Structures
Susan Thomas and Dr. Balamati Choudhury
1 Introduction
The theory of electromagnetic cloaking has been elevated from a fiction to a reality with the advent of metamaterials.Cloaking is an electromagnetic phenomenon which can bend the electromagnetic waves in an unusual way around the object. A cloak ensures scattering cancellation for any finite size physical object which enables it to be hidden from electromagnetic radiations. The constitutive parameters of the layered cloaking shells are spatially varied based on the principle of coordinate transformation in the realization of first experimentally proven invisibility cloak at microwave frequencies by [Schurig et al., (2006)]. The cloaked object and cloaking shell scatter very strongly and independently but both backward and forward scattering from the object is cancelled by the scattering from cloaking layers.
Though the dielectric permittivity tensor remains positive for the various cloaking layers, permeability tensor should range between zero and unity which is impossible with natural dielectrics [Naqui et al., (2014)]. Therefore, artificial periodic structures termed as metamaterials which exhibit unusual electromagnetic properties that can be tailored by changing the geometrical parameters of the unit cells are introduced into the design of invisibility cloaks [Choudhury et al., (2013)]. Refractive index of a metamaterial cloak is observed to be purely imaginary due to which the penetration of electromagnetic radiations into the layers is made impossible as stated by [Yuan et al.,(2008)]
The first microwave cloak consisted of 10 layers of anisotropic cloaking shells printed with resonant metamaterial structures. The extensive research on cloaking reduced the thickness of the cloaking layers with cross embedded SRRs to realize an ultrathin cylindrical cloak [Zhang et al., (2011)]. Further, though transmission line approach using non resonant structures has been introduced in the design of cloaks, it limits the size of object which can be concealed [Liu et al., (2009)]. Electromagnetic cloaks based on LC network can be implemented using multiple resonant tanks to realize dual frequency cloaks [Shao et al., (2011)] which in turn increase the complexity of the cloak design. Another approach utilizes ceramic dielectric resonators which ensure cloaking effect at specific frequencies within the resonance band [Wang et al. (2011)].Superthin square cloaks proposed using interconnected patches are also able to conceal only small objects [Wang et al., (2015)].Cloaks are used to minimize the scattering from receiver antennas and sensors improving their absorption efficiency [Soric et al.,(2014)]. This paper investigates the effectiveness of circular SRR unit cells in the realization of invisibility cloaks at microwave frequencies. The design of the circular SRR unit cell and its transmission parameters are discussed in the Section 2 and 3. The material properties for the proposed cell is extracted and analyzed in the Section 4.Further, Section 5 presents the phenomenon of existence of resonant modes in a circular SRR array.
2 Metamaterial Cloaks Using Resonant Structures
For the first practically realized electromagnetic cloak using metamaterial unit cells, a slight modification has been made in the geometrical structure of square SRR. The split in the square shaped ring is elongated towards the interior of the square shaped ring and the corners of the square SRR are kept curved. The radius of the corners as well as the length of the split determines the spatial variation of constitutive parameters of each layer. In this paper, an attempt is made to employ circular SRRs instead of square SRRs in the realization of a microwave cloak. Effective permeability being the spatially varying tensor, the metamaterial structure chosen for cloaking application should have a property to tailor the magnetic response depending on the structural parameters of the unit cell. Unlike the cloak implemented by Schurig,an attempt is made in this paper to ensure more flexibility in the design using a circular SRR. The radius of the circular SRR is invariably constant for the various cloak layers and therefore shift in resonant frequency as well as the permeability tensor values is dependent only on the length of the split.
Field excitation considerations for this novel design are same as that of the square SRR based cloak realized by Schurig. By compromising for a zero reflected power,the transformed material properties are simplified in the same way to ensure design flexibility. The variation of permeability and permittivity tensors depending on the frequency has been depicted in this paper which has not been analysed in the literature so far. Also an investigation on the resonant mode splitting (Chen et al.,2012) in a linear array of circular ring resonators is done to analyse the nature of cloak. The response of two different linear metamaterial arrays are discussed, one with unit cells in the direction of electric field and the other in the direction of propagation of wave.
3 Design and simulation of Circular SRR Based Metamaterial Cloak
The Figure 1 shows the design of circular SRR unit cell fabricated on Duroid 5870 substrate with dielectric constant of 2.33 and loss tangent of 0.0012 at 10GHz. The thickness of the substrate is 0.381mm and the split ring resonators are patterned with a thickness of 0.017mm.

Figure 1: The design of circular SRR unit cell

Table 1: Dimensions of SRR unit cell (in millimeters)
An FEM based EM design package has been used for the design and simulation of metamaterial unit cell. Here the cloaked object is a cylinder having radius equal to 23.1mm. The cloak is formed of 5 concentric layers of cylindrical dielectric sheets printed with circular split ring resonators on them. The radius of the outermost cloaking layer is set at 58.9mm. The frequency range selected for simulation is 9GHz to 13GHz. The Figure 2 shows the magnitude of transmission characteristics of the circular SRR unit cell which resonates at 10.6 GHz. The first layer of cylindrical cloak has been designed using unit cells of dimensions mentioned in Table 1.

Figure 2: Magnitude of transmission spectra (S21) for single circular SRR unit cell
The length of the split determines the magnetic response and thereby the permeability tensor for each layer of the cloak. Appropriate boundary conditions are applied to a single three dimensional unit cell to analyse the nature of cloak designed using a periodic array of the same metamaterial unit cells. The unit cell is excited with a plane wave with electric field in a direction parallel to the circular SRR plane and magnetic field normal to the surface of unit cell.
The variation of permeability tensor depending on the distance from the cloaked object can be evaluated from the transformed material properties. The plot showing the variation of permeability tensor is as depicted in Figure 3. A five layer approximation of the cloaking layers has been derived and the corresponding design parameters which result in the desired variation of permeability for the layered cloak are evaluated and given in the Table 2. The length of the split is the parameter which affects the resonant frequency as well as the permeability tensor.
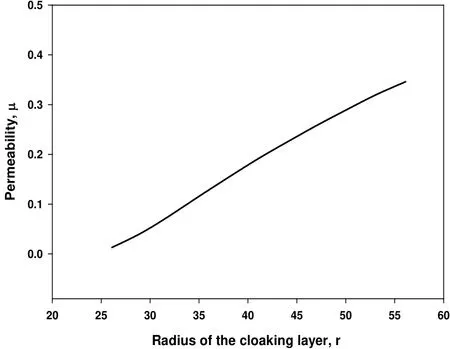
Figure 3: Variation of permeability tensor depending on the distance from center of the cloaked object
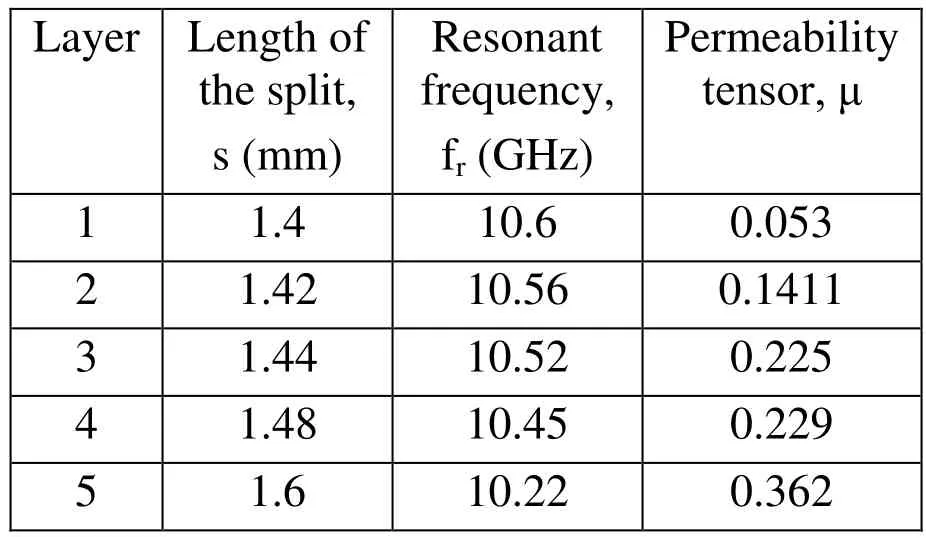
Table 2: Length of split of the SRR unit cell for each layer and its effect on the resonance and permeability tensor
4 S parameter Based Retrieval of Material Tensors of Metamaterial Unit Cell
The complex material properties such as permittivity and permeability have been extracted from simulated scattering parameters of the metamaterial unit cells using a Matlab script. The S parameter based retrieval is a reliable technique in solving the inverse problems to design the metamaterial unit cells according to the specifications for permittivity and permeability.

Figure 4: Extracted permittivity (real) variation depending on frequency

Figure 5: Extracted permittivity (imaginary) variation depending on frequency
The plot showing the variation of complex material properties depending on frequency for the first layer of cloak are as shown in Figures 4-7. The real part of permittivity is always positive in the frequency range selected for simulation, i.e., 9GHz to 13GHz.The imaginary part of permittivity and permeability are near to zero except at resonance. The real part of permeability shows an abrupt change in the value around the resonance frequency. The permeability reaches near to zero from a frequency of 11GHz to 13GHz.

Figure 6: Extracted permeability (real) variation depending on frequency

Figure 7: Extracted permeability (imaginary) variation depending on frequency
5 Resonant Mode Splitting in Finite Metamaterial Array
An array of circular split ring resonators has been designed to analyze the response and thereby the nature of cloak.The circular SRR unit cells can be arranged in a linear fashion in three different ways. An analysis of the resonant modes for each case has been discussed in this section.
5.1 Case 1: Metamaterial Unit Cells Arranged Along the Direction of Propagation Vector
The excitation of resonator array stacked along the direction of wave propagation vector as shown in Figure 8 results in a wave delay and phase difference between the SRR unit cells. This phase difference results in splitting of the resonance. When the SRRs are arranged periodically along the direction of propagation of EM wave, a split is observed in the resonant frequency.Figure 9 shows the return loss characteristics of an array with varying number of unit cells arranged horizontally, i.e. along the direction of wave propagation. The number of resonant modes is equal to the number of unit cells thereby ensuring a wide bandwidth for the cloak. Therefore the circular SRR unit cells ensure better bandwidth than the square SRR and are suitable for all cloak configurations.

Figure 8: SRR unit cells stacked along the direction of propagation vector

Figure 9: Response of resonator array arranged along the direction of propagation of wave
5.2 Case 2: Metamaterial Unit Cells Arranged Along the Direction of Electric Field

Figure 10: Stacking of SRR unit cells along the direction of electric field with (a) all unit cells oriented in one direction (b) reversed orientation for unit cell at the center
The stacking of SRR unit cells along the direction of electric field as in Figure 10(a)results in a strong resonance splitting with two narrow resonances. The simulations in free space with plane wave incidence ensued in reflection characteristic for the array as shown in Figure 11.

Figure 11: Resonant modes in array arranged along the direction of electric field with all unit cells of same orientation
5.3 Case 3: Metamaterial unit cells arranged along the direction of electric field with orientation reversed alternatively
The SRR unit cells are oriented alternatively to reduce the magnetoelectric coupling inherent in the single split SRR as depicted in Figure 10(b). When the metamaterial unit cells are arranged in the direction of electric field with the orientation of middle cell reversed, the resonance mode splitting with a deeper drop is observed as shown in Figure 12. This linear array provides a good bandwidth due to the merging of two resonances. Therefore this orientation is preferred in the propsed design of metamaterial cloak.

Figure 12: Resonant modes in array arranged along the direction of electric field with orientation reversed alternatively
5 Conclusions
A circular SRR based novel microwave cloak and its response have been thoroughly investigated.These microwave cloaks can be implemented in wireless power harvesting minimizing the scattering from receiver antennas and sensors improving their absorption efficiency. This cloaking phenomenon can also be further enhanced to be implemented in future stealth aircrafts and missiles to reduce the total scattering cross section.
Schurig, D.; Mock, J. J.; Justice, B. J.; Cummer, S. A.; Pendry, J. B.; Starr, A. F.;Smith, D. R. (2006): Metamaterial electromagnetic cloak at microwave frequencies,Science Express, vol. 314, pp. 977-979.
Naqui, J.; Martín, F. (2014): Some Applications of Metamaterial Resonators Based on Symmetry Properties, Computers, Materials & Continua, vol. 39, no. 3, pp. 267-288.
Choudhury, B.; Jha R. M. (2013): A Review of Metamaterial Invisibility Cloaks,Computers, Materials & Continua, vol. 33, no. 3, pp. 275-308.
Yuan, B.; Wang, R.; Wang, G. (2008): Refractive index in a metamaterial cloak, 8thInternational Symposium on Antennas, Propagation and EM Theory,pp. 1413-1415.
Liu, X.; Li, C.; Yao, K.; Meng, X.; Li, F. (2009): Invisibility cloaks modeled by anisotropic metamaterials based on inductor-capacitor networks, IEEE Antennas and Wireless Propagation Letters, vol. 8, pp. 1154-1157.
Shao, J.; Zhang, H.; Lin, Y.; Hao, X. (2011): Dual-frequency electromagnetic cloaks enabled by LC-based metamaterial circuits, Progress in Electromagnetics Research,vol. 119, pp. 225-237.
Wang, X.; Chen, F.; Hook, S.; Semouchkina, E. (2011): Microwave cloaking by alldielectric metamaterials, IEEE International Symposium on Antennas and Propagation (APSURSI), pp. 2876 – 2878.
Zhang, J.; Mortensen, N. A.; (2011) Ultrathin cylindrical cloak, Progress in Electromagnetics Research, vol. 121, pp. 381-389.
Chen, F.; Wang, X.; Semouchkina, E. (2012): Resonance mode splitting in split-ring resonator arrays used in the microwave invisibility cloak, IEEE Antennas and Propagation Society International Symposium (APSURSI), pp. 1-2.
Soric, J.C.; Fleury, R.; Monti, A.,Toscano, A.; Bilotti, F.; Alu, A. (2014):Controlling scattering and absorption with metamaterial covers, IEEE Transactions on Antennas And Propagation, vol. 62, no. 8, pp. 4220-4229.
Wang, J.; Qu, S.; Zhang, J.; Chen, H.; Ma, H.; Xu, Z. (2015): Design of super-thin cloaks with arbitrary shapes using interconnected patches, IEEE Transactions on Antennas And Propagation, vol. 63, no. 1, pp. 384-389.
 Computers Materials&Continua2016年6期
Computers Materials&Continua2016年6期
- Computers Materials&Continua的其它文章
- Metamaterial Inspired Radar Absorbers: Emergence,Trends and Challenges
- Analytical Estimation of Radar Cross Section of Infinitely Long Conducting Cylinder Coated with Metamaterial
- High Security Identity Tags Using Spiral Resonators
- Structural and Optical Properties of Graphene Oxide Prepared by Modified Hummers’ Method
- Automated Synthesis of Wideband Bandpass Filters Based on Slow-wave EBG Structures
