基于ATENA的钢筋混凝土无腹筋梁的非线性有限元分析
易伟建 吴羽宇

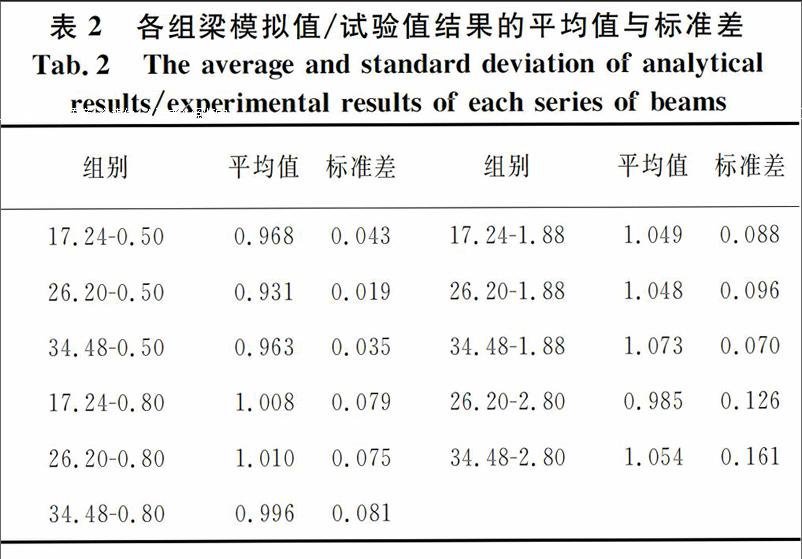
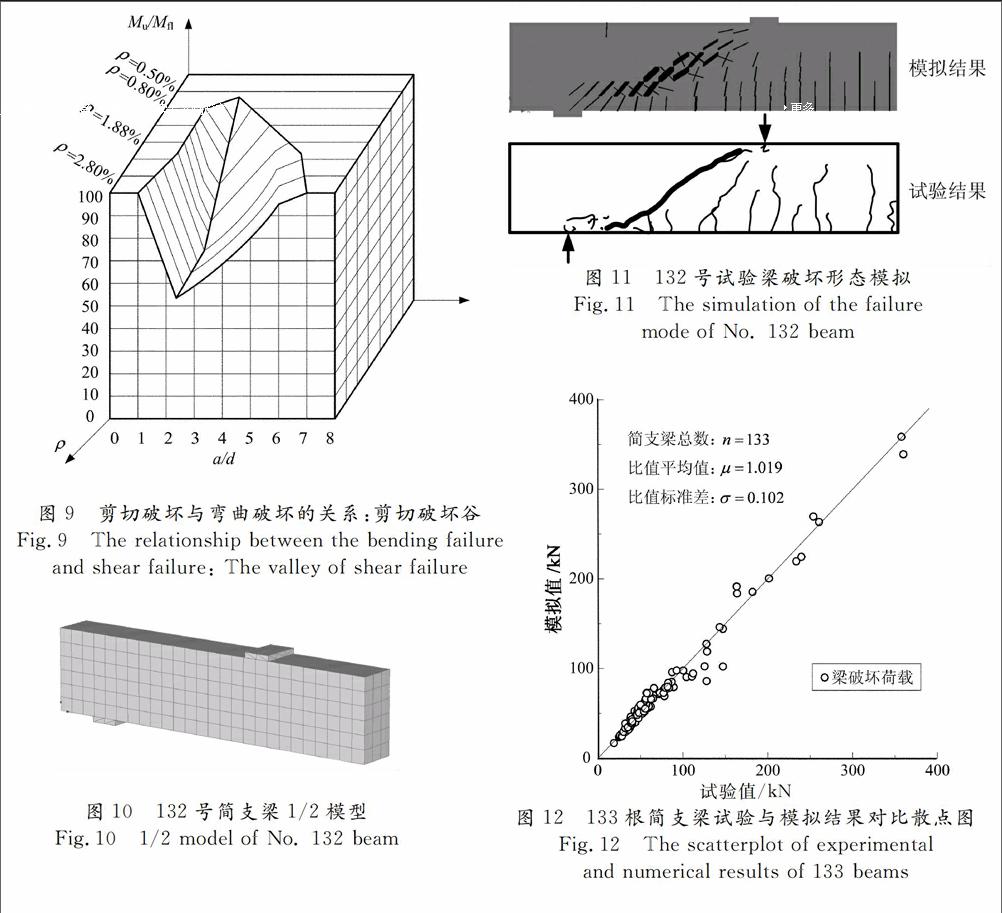
摘 要:通过ATENA软件建模对Bresler-Scordelis梁进行非线性有限元模拟,将模拟结果与试验结果进行对比,验证了所建立的有限元模型能较好地模拟无腹筋简支梁的破坏过程和破坏形态.采用已验证的有限元模型对Kani试验的133根梁进行了计算,模型能够准确地模拟试验梁的破坏荷载.通过对Kani梁计算结果的进一步分析发现,随剪跨比的增大,“拱”作用对梁受剪承载力的贡献逐渐减小,“齿”作用对梁受剪承载力的贡献逐渐增大.无腹筋简支梁名义极限剪应力随剪跨比的增大而减小,在剪跨比为2.5处,曲线发生明显转折,剪跨比小于2.5时减小幅度较大,剪跨比大于2.5后减小幅度较小.对于其他条件相同情况下的梁,在剪跨比超过2.5后,抗剪承载力减小幅度较小甚至基本保持不变,而剪跨区段的长度增大,导致破坏弯矩增大,破坏弯矩与截面计算最大受弯承载力的比值增大,因此,Kani提出的“剪切破坏谷”在剪跨比超过2.5后出现上升段.
关键词:无腹筋梁;名义极限剪应力;“拱齿”模型;有限元分析;ATENA
中图分类号:TU375.1 文献标识码:A
文章编号:1674-2974(2015)11-0001-09
自20世纪初至今,钢筋混凝土构件抗剪计算的理论和试验研究一直在不断地探索中,各国研究者们提出了大量的抗剪模型和理论.最早的桁架模型至今已有100余年.1964年,Kani[1-2]提出了“拱齿”模型对无腹筋梁的工作机理及弯剪裂缝进行解释,认为无腹筋梁的剪力传递是通过“拱齿”实现的,大剪跨比梁的受力以“齿”为主,而小剪跨比梁的受力则以“拱”为主.1980年,Hamadi和Regan[3]对齿模型进行了发展,假定裂缝方向是垂直的,且裂缝间距为梁截面有效高度的一半.1986年,Collins和Vecchio[4]在压力场理论的基础上考虑了开裂混凝土的拉应力作用,即修正压力场理论.1990年,Kotsovos[5]在试验研究的基础上提出了压力路径理论,认为压力的传递有一定的路径,与裂缝垂直的拉应力使该路径破坏,从而无法传递压力,导致梁发生剪切破坏.尽管抗剪理论研究起步较早,但由于剪切机理本身的复杂性,至今仍没有完善且受到公认的抗剪理论模型.
随着计算技术的进步,非线性有限元方法已逐渐成为钢筋混凝土结构分析和设计的一种非常有效的方法.1967年,Ngo和Scordelis[6]首次把有限单元法应用于钢筋混凝土简支梁的抗剪分析中,为钢筋混凝土有限元分析方法奠定了基础.几十年来在这一领域的大量研究[7-8]形成了丰富的成果,并集中反映在有限元分析的大型商业软件中,如ABAQUS,ANSYS等.利用非线性有限元分析软件,可以在计算模型中分别反映混凝土和钢筋材料的非线性特性,考虑或模拟钢筋与混凝土之间的粘结滑移,并在一定程度上模拟结点的构造和边界条件.软件后处理可以提供大量诸如应力、变形的全过程,结构开裂后的各种状态等结构反映信息.非线性有限元软件分析已经可以部分代替试验进行大量的参数分析,为合理的工程设计或规范修订提供依据.
ATENA软件是针对土木工程领域的一款非线性有限元分析软件.专注于混凝土结构的有限元分析,在混凝土开裂破坏和钢筋屈服方面有其独特的专业性.与其它软件相比,ATENA能够更加自由地定义材料性能,更加真实地模拟钢筋混凝土结构的行为,包括混凝土开裂、压碎和钢筋屈服等问题.该软件对混凝土结构的裂缝开展形态的模拟更是其它软件无法做到的.
本文利用ATENA软件建立有限元分析模型,先对Bresler-Scordelis的试验梁进行模拟分析,说明模型的适用性.而后对Kani的无腹筋梁受剪试验进行有限元模拟,将模拟结果与试验结果进行对比,并绘制“剪切破坏谷”.最后,以有限元数值模拟结果为基础,揭示“拱”作用以及“齿”作用对梁承载力的贡献随剪跨比增大而变化的情况,并进一步解释Kani提出的“剪切破坏谷”.
1 ATENA模型验证
1.1 试验简介
1963年,美国加州伯克利分校的Bresler和Scordelis两位教授在ACI发表了一篇钢筋混凝土简支梁抗剪性能试验研究的论文[9],试验数据的可靠性得到公认使之成为所谓的Benchmark试验而被计算分析广泛引用进行模型校核.2004年,加拿大多伦多大学的Vecchion教授重复了Bresler和Scordelis的试验[10],证明当年的试验观测结果是可以重现的.因此,可以采用Bresler和Scordelis的试验结果对有限元分析模型进行校核.由于Kani试验缺少梁剪切破坏时的极限挠度数据,也需要另外选择试验结果对ATENA有限元模型进行验证.
1.2 模型建立及相关材料参数取值
ATENA为不同的研究目的研究对象提供了丰富的材料模型[11].
本文分析的混凝土单元采用3D Nonlinear Cementitious 2单元,此单元采用非关联塑性的混凝土断裂塑性模型[12],将断裂模型与塑性模型相结合以描述结构的受拉(开裂)和受压(塑性)性能.该混凝土模型的单轴应力应变关系曲线以及双轴失效曲线分别如图2和图3所示.混凝土抗压强度指标为圆柱体抗压强度指标f′c[11],直接采用试验值.其余参数均取软件默认公式计算结果,默认公式来自于CEB-FIP Model Code 1990[13]及一些其他研究资料的相关规定与建议.
ATENA使用弥散裂缝模型,假定裂缝均匀地分布在单元内部而不是发生在单元之间.将混凝土材料处理为各向异性材料,利用混凝土的材料本构模型来模拟裂缝的影响[14].裂缝模型分为定角裂缝模型和转角裂缝模型.ATENA通过设置定角裂缝系数来对上述两种模型进行选择,根据大量的数值模拟算例可知定角裂缝模型的计算结果更接近实际结果.因此,将定角裂缝模型系数设置为1.0.

