基于Copula—VaR的市场风险管理研究

作者简介：苏英洁（1992-），女，汉族，四川广汉，研究生，西南财经大学，研究方向：西方经济学。

本文随机选取8支股票：山煤国际（600546）、浦发银行（600000）、中金黄金（600489）、东方航空（600115）、中国平安（601318）、农产品（000061）、威孚高科（000581）、中国联通（600050）8只股票，在Copula-VaR模型的基础上进行实证检验。定义2013年1月1日至2015年3月15日为样本时间区间，股票日收盘价为股票价格，数据来源于财富证券交易数据库。

为保证样本收益率数据的可靠性，本文对样本数据进行了一系列的处理。首先，由于单权的日收盘价格可能会使得收益曲线出现异常波动，因此本文对样本数据的日收盘价进行了向前复权处理。其次，在2013年1月1日至2015年3月15日的样本期间内，样本组合中8家上市公司分别存在不同时段的停盘，这些不等时停盘会影响最终结果的准确性，故用样本股票前一日的收盘价格替代了其停盘日的收盘价格。

一、数据描述统计及模型选择

由于市场风险分布曲线不对称性情形时常出现，使用正态分布来描述金融资产收益率不一定合理。以下是对8支股票收益率的描述性统计：

从表1可以看出，8支股票的收益率存在较明显的尖峰、厚尾特征，各变量之间相关性也较强。大量的实证结果证明，金融资产的价格波动具有杠杆效应，这跟经典GARCH模型的金融资产收益涨跌对其波动率影响程度等同的观点有悖。实际上，在市场价格下跌时的金融资产价格波动要远远大于市场价格上涨时的价格波动。因此，本文选取能够更好地描述金融资产波动性特征的EGARCH模型。另外，由于EGARCH模型不是对条件方差直接建模，而是对条件方差的对数间接建模。因此，本身就包含条件方差必须是正值的隐含条件，这也减弱了经典GARCH模型的参数限制，使模型的灵活性和简便性大大增加。在前面分析的基础上，本文采用EGARCH（1，1）模型来描述该资产组合风险的边缘分布函数。根据定义，EGARCH（1，1）-Normal模型的数学表达式如下：

二、模型参数估计

依次选取t-Copula、Gumbel Copula、Clayton Copula和Frank Copula这四种常用的Copula连接函数，分别求对数极大似然函数（见表2），接着根据拟合效果挑选最优的模型进行实证检验。

比较AIC值的大小，t-Copula对应的值要比Gumbel Copula、ClaytonCopula和Frank Copula的AIC值小，并在统计意义上显著。根据AIC准则，AIC值越小，模型的精确度就越高。因此本文认为t-Copula模型是最优模型，能够更好地拟合各样本收益序列的边缘分布。

三、投资组合风险度量

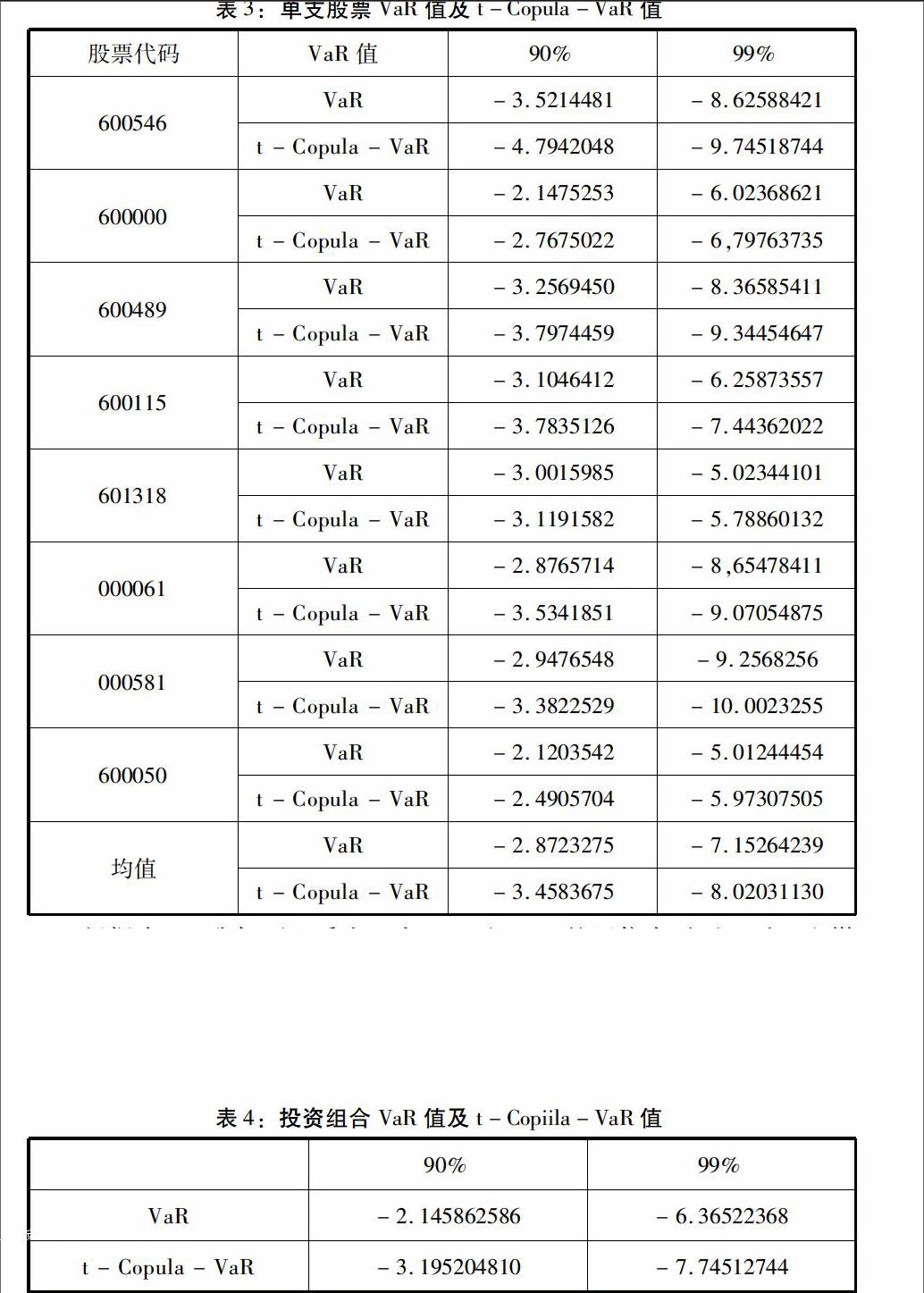
根据表3，我们可以看出，在90%和99%的置信水平下，对于山煤国际（600546）、浦发银行（600000）、中金黄金（600489）、东方航空（600115）、中国平安（601318）、农产品（000061）、威孚高科（000581）、中国联通（600050）8只股票，t-Copula-VaR模型模来的风险值都要大于传统的VaR模型估计出来的风险值。

同样，根据表4可以看出，对于投资组合而言，无论在90%还是99%的置信水平下，t-Copula-VaR模型的组合风险值都要大于VaR模型对应的值。说明不管是单只股票还是投资组合的风险度量，t-Copula-VaR模型都更为准确，能让投资者在构建股票投资组合时，有效降低因忽视潜在风险所造成的影响。此外，结合表3和表4还能得出，无论在哪个置信度水平下，表4投资组合的t-Copula-VaR和VaR值都要大于表3中各支股票t-Copula-VaR和VaR值的均值，这说明了投资组合可以有效降低单只股票之间的非系统性风险。

最后，根据投资组合的Copula-VaR值以及单只股票的Copula-VaR值，我们还可以发现，在构建这8支股票的投资组合时，我们应减少持有风险值大的股票仓位，增加风险值小的股票比重，即在投资组合中，可以相对增加在浦发银行、东方航空、中国平安和中国联通这4只股票的仓位和权重，减少在山煤国际、中金黄金、农产品和威孚高科的仓位和比重，以得到最优、最合理的收益与风险。（作者单位：西南财经大学）