基于混合MADM的中小企业信用风险计量研究
宋瑞敏 王冠雄 汪亭
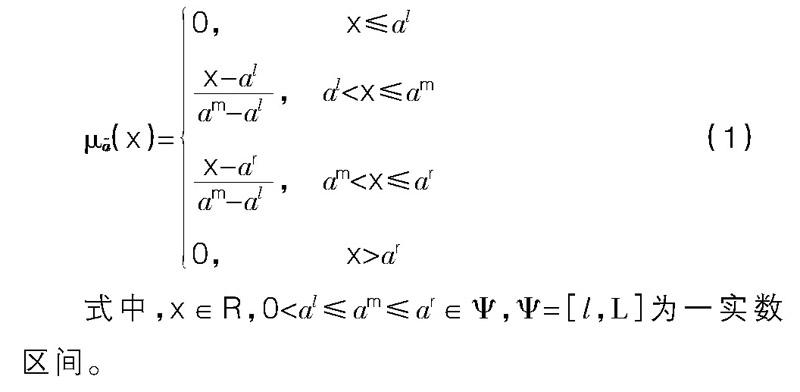


【摘 要】 文章在单一数值型指标信用风险计量模型的基础上,引入了区间值型指标和三角模糊数型指标,使得整个信用风险评估体系更具科学性和可操作性。研究发现,混合多属性决策方法不仅可以拓展信用风险指标空间,还能直观地反映出多个待评估对象的信用风险差异化程度,从而为金融机构衡量企业信用风险水平提供有效解决路径。
【关键词】 信用风险评估; 混合多属性决策; 风险指标; TOPSIS方法
中图分类号:F830.5 文献标识码:A 文章编号:1004-5937(2016)06-0048-04
一、引言
作为三大金融风险之一的信用风险贯穿于整个金融交易过程,随着金融业的不断发展,对信用风险的计量与管理也变得更为复杂。目前我国金融市场尚处于高速发展阶段,中小企业融资渠道主要集中于向银行贷款融资,而商业银行在面对鱼龙混杂的中小企业时,企业实际违约数据及相关统计资料的严重缺失加剧了双方的信息不对称程度,使得我国商业银行体系饱受信用风险集中、不良贷款率高等问题的困扰。
20世纪90年代末期金融危机的爆发,大量银行信贷损失惨重,使得金融界普遍关注对信用风险的计量,在此期间涌现出很多信用风险水平计量模型,如KMV模型、J.P.摩根开发的Credit Metrics模型以及瑞士信贷银行基于保险精算的Credit Risk模型和麦肯锡的Credit Portfolio view模型,至此,现代意义上科学的信用风险计量与管理才真正发展起来。2004年颁布、2006年开始正式在各成员国实施的新巴塞尔协议中,在保留原巴塞尔协议核心原则的基础上,更加重视对信用风险的评估与计量,并提出内部评级法(Internal Rating Based)鼓励银行使用自己的内部模型计量信用风险。
国内关于信用风险的计量研究多数集中于验证上述模型的可靠性以及结合我国国情对上述模型的改进。如张乐(2014)通过研究国际上常用风险计量模型方法与我国商业银行的信用风险管理的适用性发现,这些模型并非均适合我国的商业银行。孙小丽(2013)利用我国上市公司ST公司和非ST公司的相关数据进行测算,说明了KMV模型能够较好地测算我国上市公司的信用风险水平,同时,考虑到我国实际情况,提出更适合中国商业银行信用风险评估的KMV模型改进方法。也有相关学者在计量方法上提出新的思考和尝试,如原毅军、吕品等(2012)把多属性决策方法应用于商业银行的信用风险评估中,能够基于商业银行自身的信用风险指标,客观地比较多家商业银行的信用风险水平。周丽莉、丁东洋等(2011)为了缓解数据缺失和测量误差以及债务人异质性等问题,提出了贝叶斯模型中分层先验信息和马尔科夫链蒙特卡洛(MCMC)模拟方法。本文在现有研究基础上,提出了利用含有精确值、区间值以及模糊数值三类属性值的混合多属性决策方法来对中小企业进行信用风险评估,综合考虑了专家意见、企业自身参数等多个指标,为金融机构作出放贷决策提供有力依据。
二、定义及运算法则
为了便于下文中指标矩阵的规范化以及指标权重的计算,现给出区间值及三角模糊数的定义,以及部分运算法则。
定义1:记a=[al,ar]为闭区间数,其中al,ar∈R且al≤ar,R上的全体闭区间数记为R。
定义2:记=(al,am,ar)为三角模糊数,如果其隶属函数为?滋(x):R→[0,1],即:
?滋(x)=0, x≤al, al
式中,x∈R,0 根据扩展原理,对任意两个三角模糊数=(al,am,ar)和=(bl,bm,br)有+=(al+bl,am+bm,ar+br),λ·=(λal,λam,λar)。 对任意两个闭区间数a=[al,ar]和b=[bl,br],其线性运算法则如下: a+b=[al,ar]+[bl,br]=[al+bl,ar+br],λ·a=λ·[al,ar]=[λal,λar],λ>0,λ∈R 三、中小企业信用风险评估的混合多属性决策模型 在中小企业信用风险评估过程中,存在大量的混合型多指标决策问题,如企业的资产净利率、财务杠杆系数等指标可以用精确的数值表示出来,而诸如企业员工的素质、业务水平,企业自身的管理水平,企业文化等,这些指标无法用定量的数值语言描述,而是以多种形式出现在决策矩阵中,形成了混合型多属性决策问题。利用混合型多属性决策方法的优势在于:其一,能综合考虑定量指标、定性指标和区间数指标,使得整个评估系统更面面俱到;其二,能够直观地反映出多个待评估对象信用风险水平的差异化程度;其三,其最终结果是以排序的方式,把所需考虑的目标企业按信用等级进行排序,这样可为金融机构在选择放贷对象时提供有力依据。 现假设有A1,A2,…,Am家中小企业,商业银行在进行放贷时会考虑C1,C2,…,Cn,n∈N*个指标来考察企业的信用水平,则各企业属性指标矩阵为: A=c11 c12 … c1nc21 c22 … c2n… … … …cm1 cm2 … cmn 其中cij为第i个企业在第j个指标下的评价值,且第一到第h1个指标为三角模糊数型指标,第h1+1到第h2个指标为精确数值指标,第h2+1到第n个指标为区间值指标。 1.属性矩阵规范化 对于不同类型的指标值,其规范化的方式也有所不同,下面给出各类型指标值的规范化方法。设规范化后的矩阵为B=(bij)m×n,对于精确实数值指标,无论是成本型指标还是效益型指标,其规范方法均为bij=,对于区间数规范方法则要区分指标类型为成本型还是效益型,规范方法如下: blij=ailjbrij=airj,效益型指标,i∈N;
或blij=(1?蛐aiuj)brij=(1?蛐ailj),成本型指标。
对于三角模糊数,也要区分成本型指标或效益型指标,采取不同的规范方法,如下:
blij=ailjbmij=aimjbrij=airj,效益型指标;
或blij=(1?蛐aiuj)bmij=(1?蛐aimj)brij=(1?蛐ailj),成本型指标。
2.计算各指标权重,本文采用熵权法求各指标的权重?棕j
对于精确数值指标,首先计算第j个指标下第i个企业指标值的比重Pij=cij cij,然后计算第j个指标的熵值ej=-kPijlnPij,其中k=1/lnm,最后算得第j个指标的熵权?棕j=(1-ej)(1-ej)。
对于三角模糊数=(al,am,ar)指标,根据均值面积度量法,将其转换为s()=(al+2am+ar)/4。对于区间数,利用区间数排序的一种联系数方法(王万军,2009),将区间数值转化为实数值,然后按照精确值的熵权法计算指标权重。
利用熵权法求得权重向量?棕,对已经规范化的矩阵B=(bij)n×m求加权矩阵R=(rij)m×n。
3.利用多属性决策中的TOPSIS方法,对所考察企业信用风险进行排序
TOPSIS方法的核心问题是求出正负理想解,并通过比较各方案到正负理想解的距离来判断各方案的优劣顺序。
对于精确数值型指标,令V+j=V-j=;对于区间型指标,令t-j=,t+j=s-j=,s+j=;对于模糊型指标,令M+j=max{r1j,r2j,…,rnj}M-j=min{r1j,r2j,…,rnj},则其正理想解为X+=(M+1,…,M+h1,V+ h1+1,…,V+h2,[t- h2+1,t+ h2+1],…,[t-n,t+n]),其负理想解为X-=(M-1,…,M-h1,V- h1+1,…,V-h2,[s- h2+1,s+ h2+1],…,[s-n,s+n])。
每个方案到理想解的距离为d+i=d(Xi,X+)=
其中:d+ij=d(rij,M+j)+d(rij,M+j),i=1,2,…,m;j=1,2,…,h1V+j-rij,i=1,2,…,m;j=h1+1,…,h2r-ij-t-j+r+ij-t+j,i=1,2,…,m;j=h2+1,…,n
每个方案到负理想解的距离为d-i=d(Xi,X-)=
其中:d-ij=d(rij,M-j)+d(rij,M-j),i=1,2,…,m;j=1,2,…,h1rij-V-j,i=1,2,…,m;j=h1+1,…,h2r-ij-s-j+r+ij-s+j,i=1,2,…,m;j=h2+1,…,n
每个方案到正理想解的相对贴近度为di=,i=1,2,…,m,用相对贴近度的大小来衡量各方案的优劣。
四、中小企业信用风险指标选取
中小企业既有一般企业的共有特征,也因自身的特殊性有其区别于一般企业的固有特征。故在对中小企业做信用风险评估时,指标选取得当与否直接关系到模型的可靠性。本文参考国内外研究成果及我国特殊国情,选取以下指标来衡量企业信用风险水平。
首先考察企业基础素质情况。选择管理效率(C1)和资产质量(C2)来反映待考察企业的基础素质情况。由于这两个指标均无法用定量化的语言描述,常常靠专家评价来反映两个指标的优劣情况,故借助三角模糊数,把这两个指标的语言值模糊化,其一一对应关系如下。
语言值:{极低,很低,低,较低,一般,较好,好,良好,很好},对应的模糊数分别为{,,,,,,,,}。
接着考察中小企业的财务状况。反映企业财务状况的指标很多,本文选取几个比较典型的指标作为评估参数,如资产负债率(C3)=负债总额/资产总额,较高的资产负债率意味着企业负债经营程度高,财务风险较大,但这也并不意味着资产负债率越低越好;流动比率(C4)=流动资产/流动负债,该指标是衡量企业短期还债能力的重要参考依据;资产净利率(C5)=净利润/平均资产总额,反映了企业每一元资产的盈利能力;财务杠杆系数(C6),衡量企业财务风险的重要指标。
最后考察企业的发展能力指标。这里主要考察企业的利润增长率水平(C7)和新产品投产率水平(C8)。前者反映了企业盈利能力上升的幅度,该指标越大,则企业偿债能力越强;后者则反映了企业的创新能力,毫无疑问创新能力是现代企业赖以生存的必备条件。
五、算例分析
本文选取四家中小企业作为研究对象,应用混合型多属性决策模型,对上文中选取的八个信用评估指标进行分析,为这四家企业的信用水平进行排序。四家企业A、B、C、D的各属性指标值如表1所示。
按照模型中精确值、区间值、三级模糊数值各自的规范化公式,对表1中企业信用指标属性值作归一化处理,用矩阵B表示。
通过熵权法求得各属性权重如表2。
对已经规范化的矩阵B,求加权矩阵R。
求得正负理想解分别为:
X+ = [(0.0226, 0.0289, 0.0371), (0.0122, 0.0161,
0.0213), 0.1030, 0.0149, 0.0550, 0.0113,[0.2627,
0.4028],[0.1214,0.1837]]
X- = [(0.0113, 0.0160, 0.0223), (0.0070, 0.0101,
0.0142), 0.0344, 0.0094, 0.0229, 0.0078,[0.0438,
0.1148],[0.0243,0.0612]]
求得每个方案到正负理想解的距离为:
d+1=0.1719,d-1=0.3970;d+2=0.4644,d-2=0.1053;
d+3=0.5190,d-3=0.1259;d+4=0.0326,d-4=0.5568
求得每个方案到正理想解的相对贴近度为:
d1=0.6978,d2=0.1848,d3=0.1952,d4=0.9446
以上相对贴近度的现实意义是,其值越接近1,其信用水平越高,所面临的信用风险也就越小;相反,其值越接近0,信用水平越低,面临的信用风险也就越高。因此在计量信用风险时,可以用1减去每个方案到正理想解的相对贴近度,得出的结果就是该企业的信用风险值。从以上结果可知,四家企业的信用水平顺序为d4>d1>d3>d2,从而得到金融机构为这四家企业提供融资帮助时所面临的风险顺序为企业B>企业C>企业A>企业D,且容易发现,企业B、C的信用风险水平接近,但要远远高于企业D和企业A。
通过理论模型和算例分析可知,混合多属性决策模型不仅可以为多个待评估对象的信用风险水平排序,而且能够直观地反映出各对象之间的信用风险差异,从而为决策机构提供更可靠的决策依据。
目前我国的金融信用风险评估体系还不完善,也没有一个权威的指标选取标准,混合多属性决策方法的科学性和进步性在于,理论上可以将所有被认为正确的指标纳入模型。其在计量信用风险时,不仅可以考虑精确值属性指标,也能覆盖区间值指标以及模糊数值指标,可以直观地比较出多个方案的优劣顺序,其缺点是不能对单个企业作信用风险评估。在我国,中小企业自身存在诸多问题,信息的不对称使得金融机构在面对多个放贷对象时往往不知所措。利用混合多属性决策的方法,可以从企业自身的信用风险指标入手,结合行业内专家的主观定性判断,便能为金融机构放贷提供可靠的决策依据。
【参考文献】
[1] CROSBIE P.Modeling default risk[M].San Francisco:KMV corporation,2003.
[2] MORGAN J P. Risk metrics-technical document[M].New York:J.P.Morgan Inc.
[3] 张乐.现代信用风险计量方法与我国商业银行的信用风险管理研究[J].开发研究,2014(5):114-118.
[4] 孙小丽.基于KMV模型的商业银行信用风险测算研究[D].北京:北京邮电大学,2013.
[5] 原毅军,吕品,李聪,等.多属性决策方法在商业银行信用风险评估中的应用[J].南京审计学院学报,2012,9(2):17-21.
[6] 周丽莉,丁东洋.基于MCMC模拟的贝叶斯分层信用风险评估模型[J].统计与信息论坛,2011,26(12):26-30.
[7] 夏勇其,吴祈宗.一种混合型多属性决策问题的TOPSIS方法[J].系统工程学报,2004,19(6):631-634.
[8] 龚承柱,李兰兰,卫振锋,等.基于前景理论和隶属度的混合型多属性决策方法[J].中国管理科学,2014,22(10):123-125.
[9] 吴冲,万翔宇.基于改进熵权法的区间直觉模糊TOPSIS方法[J].运筹与管理,2014,23(5):43-45.
[10] 王万军.区间数排序的一种联系数方法[J].计算机工程与设计,2009,30(8):2056-2057.

