利用HMM算法确定重组自交系基因型

摘要：重组自交系是杂交一代经过连续自交而获得的自交系群体。隐形马尔科夫模型（HMM）是一种极大似然估计算法，在很多生物信息研究中取得了理想的结果。文章提供了利用一阶隐型马尔科夫模型来确定重组自交系个体基因型的方法，并论述了其准确性和时效性。该算法在模拟数据及小鼠基因型数据上取得了理想的结果。

关键词：重组自交系；HMM算法；生物信息；隐形马尔科夫模型；极大似然估计算法 文献标识码：A

中图分类号：S511 文章编号：1009-2374（2016）08-0022-02 DOI：10.13535/j.cnki.11-4406/n.2016.08.012

生物的基因组中蕴含着丰富的遗传信息。随着测序技术的不断发展，通过对不同生物的基因组测序，人们发现，在不同个体的染色体上，99%的碱基信息都是相同的，而另外1%的差异造就了不同个体差异。这些单个碱基上的不同也叫单核苷酸多态性（SNP）。单核苷酸多态性也是主要的可遗传变异。现如今，研究遗传变异不仅限于单个的SNP。在遗传的过程中，不同基因座位的基因并不是完全随机地形成单体型，而是某些相邻基因座位上的基因同时出现的概率总是比较大，这种现象叫做连锁不平衡。现在越来越多的研究利用全基因组的SNP信息进行关联分析。通过全基因组关联分析等研究，已经在植物和动物中发现了很多关键基因。

在全基因组关联分析等诸多研究中，生物学家常常通过构建重组自交系，然后对重组自交系进行测序整理，确定重组自交系的基因型，为关联分析提供输入数据。随着测序技术的发展，人们可以通过对DNA、RNA片段进行测序而获得重要的数据。然而由于测序成本昂贵，测序深度不足，导致测序存在一定的误差，对测序数据处理并进行基因分型得到的数据同样也会存在一定误差。为了减小这种误差，并且不依赖于昂贵的测序成本费用，文章利用隐形马尔科夫模型（HMM）算法来提高测序数据的准确性。

1 重组自交系

重组自交系是杂交一代结果连续自交获得的。如果是二倍体生物，基因组由两条染色体组成，其中一条来自父亲，另一条来自母亲。在遗传的过程中，当两个个体进行杂交时，在减数分裂时期，同源染色体间会发生交换。通常根据研究的目标及生物学意义选择两个亲本，记为亲本1和亲本2，经两个亲本进行杂交，在后代中不断选择合适的个体进行自交。进过多代自交，并经过培养环境或自然环境的选择后，就会得到较好的纯合自交系结果。当染色体上存在不同的等位基因时，其中一个等位基因作为遗传信息遗传给自交后代。

染色体上的等位基因一般只存在两种，即A、C、G、T中的两种。当杂交后代经过不断自交后，绝大部分染色体区域将被纯化，也存在少部分不易被纯化的区域。在对基因型进行基因分型之后，在每个座位上，一般的，当基因型来自于亲本1时被标记为0，来自于亲本2被标记为2，如果是杂合的情况，该位置被标记为1。有时也将基因型来自于亲本1位点的标记为AA，来自亲本2的位点标记为HH，杂合的位点标记为AH。本文采用第一种标记方法，并用此标记方法来描述隐型马尔科夫过程。

2 隐形马尔科夫模型在重组自交系中的应用

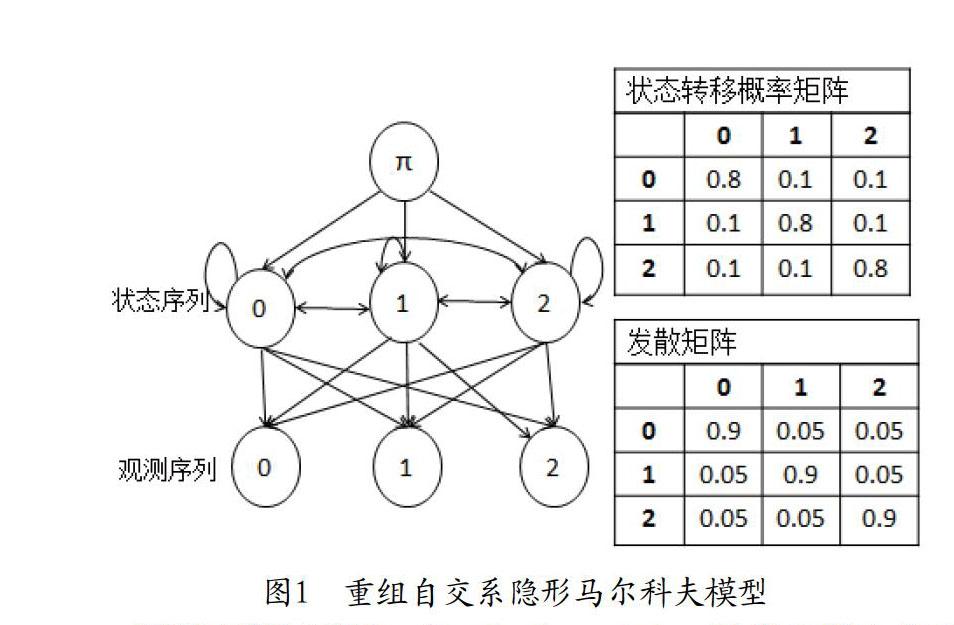
隐形马尔科夫模型是加入隐含状态的马尔科夫模型，最早由Baum等人提出。隐型马尔科夫模型的状态值是隐藏的、不可见的。隐型马尔科夫模型可以通过可观测到的数据推测不可观测的数据。隐形马尔科夫模型是一个双重自动机，它描述状态之间的转移过程，并描述状态值与观测值之间的对应关系。通过概率分布将它们联系在一起。

隐形马尔科夫模型由五元组λ=（S，O，π，A，B）来描述，其中S为状态值集合，O为观测值集合，π为初始状态，A为状态转移概率矩阵，B为发散概率矩阵（特定状态下产生每个观测值的概率）。文章中采用一阶马尔科夫模型，即每一个状态仅依赖于前一个状态。在重组自交系中，状态和观测值均由基因型组成。对于每一个群体中的个体，包含三种状态和三种观测值，即S={0，1，2}，O={0，1，2}，样本的SNP的序列为观测序列，样本SNP的待估计序列为状态序列。

假设观测序列X={}，对于重组自交系首先要求参数A、B的最优估计值。用给定的观测序列X来优化模型λ，使概率达到局部最大。本文优化模型参考Baum-Welch。给定初始化参数，在当前参数情况下，在局部估计最优状态序列。在新的最有状态序列下重新估计参数，不断迭代直到λ收敛。

当获得最优的参数λ后，在所有的状态路径中，找出使观测序列概率最大的状态路径R，即：

通过不断迭代，更新转移概率矩阵和发散矩阵，当矩阵收敛时，获得概率似然最大的状态序列。在重组自交系中，将隐马尔科夫模型的学习问题和解码问题结合起来，编写了一个适合于重组自交系的软件包。

3 算法运行及结论总结

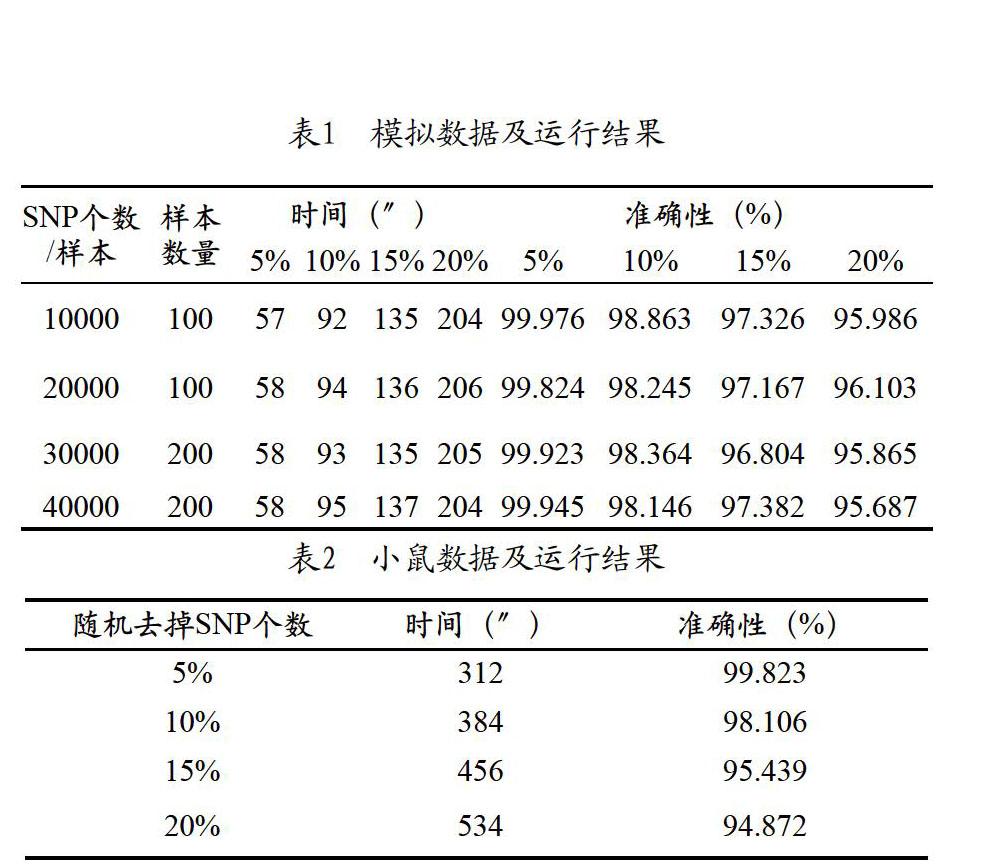
第一，为了验证程序的准确性及其效率，文中模拟了不同样本数量，不同SNP数量的重组自交系群体，模拟数据具体信息如表1所示。除模拟数据以外，从http：//mouse.cs.ucla.edu/mousehapmap/获得了小鼠已验证的自交系群体的单体型数据，小鼠的数据中包含99个家系，每个家系包含大约10万个SNP。对于模拟数据和小鼠自交系的数据，分别随机修改其中5%、10%、15%、20%的位点。在模拟数据及小鼠数据上运行HMM算法，将运行结果与修改前的原始数据进行比较。实验结果如表1和表2所示，表格中记载的为单个样本的时间。如果运行环境相同，每个样本的迭代过程均一样，耗时也一样。从表中可以看出，结果的准确性超过94%，当样本量增加时，时间会线性增长。

第二，重组自交系对于全基因组关联研究、表达数量性状研究等有重要意义。在很多研究中已通过相关研究确定了很多重要的位点，找到了很多影响某些性状的关键基因及一些重要的致病基因。隐型马尔科夫模型在序列比对、识别CpG岛等生物信息学方面也取得了显著的成就。理想的重组自交系决定了之后的研究是否顺利以及是否正确，文章提供的算法很好地解决了这个

问题。

参考文献

[1]将红敬.HMM及其在生物信息学中的应用[D].中南大学，2011.

[2]王子坤.随机过程论[M].北京：科学出版社，1965.

[3]Birney E.Hidden Markov Models in biological sequence analysis[J].IBM Journal of Research and Development，2011，45（364）.

[4]L.E.Baum.An Inequality and Associated Maximization Technique in Statistical Estimation of Probabilistic Functions of Markov Process[J].Inequalities，1972，3（1）.

[5]Burke，C.J，M.Rosenblatt.A Markovian function of a Markov chain[J].Ann.Math.Stat，1958，（29）.

作者简介：贾瑶丽（1989-），女，山西长治人，北京交通大学硕士研究生，研究方向：数据挖掘。

（责任编辑：黄银芳）