数学之“美”

古希腊伟大的哲学家亚里士多德早就指出：“认为数学的科学全不涉及美或善是错误的……数学的科学特别体现秩序、对称和明确性，而这些正是美的主要形式。”笔者认为数学中的美感俯拾即是，在解题教学中，可尝试对学生进行数学美的熏陶。

一、简洁美

爱因斯坦说过：“美，本质上终究是简单性。”他还认为，只有借助数学，才能达到简单性的美学准则。数学解题中的“简洁美”有很多，以下仅举一例。

运用整体思想，且用字母代替原题中的两个式子，复杂的计算问题解决得简洁而明快，充分体现了数学问题解决中的“简洁美”。其实，数学中最为简洁的美莫过于欧拉公式V-E+F=2，顶点数V，棱数E，面数F，如此简单的一个公式，不计其数的多面体，都必须服从它。需要说明的是数学语言本身和数学中的许多公式和定理本身就体现了“简洁美”。

二、异曲同工美

数学中的许多问题可以用不同的方法去解决，最后得到的结果无论在形式上和实质上都是一致的，体现了数学本身的内在统一，可谓“异曲同工”。

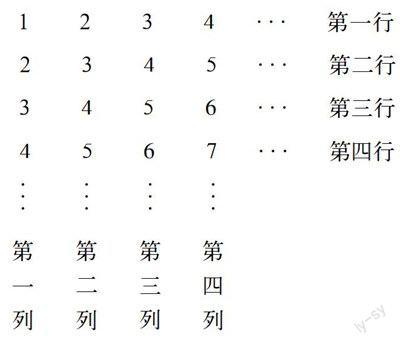
根据表中所反映的规律，猜想第n行（n为正整数）与第n列的交叉点上的数应为               。

【方法一】先考察特殊的情形第一行第一列交叉处的数为1，第二行第二列交叉处的数为3，第三行第三列交叉处的数为5，第四行第四列交叉处的数为7，根据此规律这一串数为1，3，5，7…所以第n行第n列交叉处的数为2n-1。

【方法二】考察行列交叉处的数与行数和列数的关系，这个数等于行数与列数的和减去一。例如，第3行第3列交叉处的数为5=3+3-1，所以第n行第n列交叉处的数为n+n-1=2n-1。

实际上方法一中的每行每列交叉处的数都可以写成方法二中的形式，两种不同的方法结果一致，可谓“殊途同归”。

三、和谐美

我国著名的数学家华罗庚曾说过，“数缺形时少直观，形少数时难如微;数形结合百般好，隔离分家万事休”。数学中数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定的条件下，数和形之间可以相互转化，相互渗透。

【例3】，求1+2+3+…+n的值，其中n为正整数。对于这个求和问题，如果采用纯代数的方法（首尾两头加），问题虽然解决了，但在求和的过程中，需对n的奇偶性进行讨论。

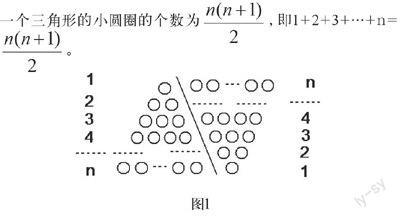
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那会非常直观。现利用图形的性质来求1+2+3+…+n的值，方案如下：如图1，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的。而组成整个三角形的小圆圈的个数恰好为1+2+3+…+n的值，现把左边三角形倒放于斜线的右边，与原三角形组成一个平行四边形。此时组成平行四边形的小圆圈共有n行，每行有（n+1）个小圆圈，所以组成平行四边形小圆圈的总个数为n（n+1）个，因此，组成一个三角形的小圆圈的个数为，即1+2+3+…+n=    。

（1）仿照上述数形结合的方法，设计相关图形，求1+3+5+…+（2n-1）的值，其中n为正整数。（要求：画出图形，并利用图形做必要的推理说明）

（2）试设计另外一种图形，求1+3+5+…+（2n-1）的值，其中n为正整数。（要求：画出图形，并利用图形做必要的推理说明）

【解析】其中（1）的做法和原题中的方法相类似，这里不再赘述，第（2）小题可画出如图2的图形，第一个直角中有1个小圆圈，第二个直角中有3个小圆圈，第三个直角中有5个小圆圈……第n个直角中有（2n-1）个小圆圈，组成整个正方形的小圆圈的个数恰好为1+3+5+…+（2n-1）的值，另一方面正方形每行有n个小圆圈，共有n行，所以小圆圈的总数为n²个，即1+3+5+…+（2n-1）= n²。

这个问题中数和形是如此的和谐统一，不得不令人惊叹，在解题中我们深刻感受到了数学的美轮美奂。

四、奇异美

解题中的奇异美是指题中得出的结论或解题方法出人意料，让人感到诧异和惊奇。例如，最近几年中考试题中经常出现的七巧板拼图问题，让学生尽情领略到数学的奇异之美。用七块板可以拼成一个最简单的正方形，也可以拼出千变万化的复杂图案，如人形、鸟兽、花草、房屋等。学生所能拼出的图案之多之美，出人意料。数学题有一般的规律和一般的解题模式，但每道数学题也都有各自特殊的性质，这些特殊的性质构成了数学的奇异美，根据数学的奇异美。在求解某些数学问题时，要打破常规，突破现成的思维模式，找到别开生面、出奇制胜的解法。

总之，教师在解题教学中若能把数学问题中这些美学本质挖掘出来，必能提高学生学习数学的兴趣，激发学生对数学美的体验，启迪学生的思维，开拓学生的视野。因此在解题教学中对学生进行美的熏陶值得一试。

周凌峰，男，周庄中学校长、党支部书记，曾在2011年8月受教育局指派，赴山西省吕梁市离石区支教。荣获“江阴市青年教师教学大比武一等奖”“江阴市优秀共产党员”“江阴市优秀班主任”“江阴市教学能手”“江阴市优秀教育工作者”“离石区优秀班主任”“吕梁市离石区五一劳动奖章”“无锡市青年教师评优课一等奖”“无锡市优秀教育工作者”“无锡市教学能手”“感动山西特别奖”等称号。

教科研方面注重实效，参与编辑《初中数学知识表解》一书，参与国家级重点课题“创新型教师培养”、江苏省重点课题“构造积极心理场”，独立主持无锡市教师专项课题“概念图在数学教学中的应用”。《求导诚可贵，构造价更高》《例谈数学教材中的例题和习题教学》《追求“我”的课堂》《探索向量问题求解 彰显数学思想魅力》等论文发表于《理科考试研究》等杂志，并有多篇文章在全国、无锡市、江阴市各类评比中获一、二等奖。