测方向三角网函数模型与测角网函数模型解算结果的比较分析
王振
(山东省地质矿产勘查开发局第五地质大队,山东 泰安271000)
测方向三角网函数模型与测角网函数模型解算结果的比较分析
王振
(山东省地质矿产勘查开发局第五地质大队,山东 泰安271000)
在传统的三角网测量中,如果观测值是角度,可以分为测方向三角网和测角三角网。本文通过一个算例,分别以方向观测值和角度观测值为平差时的观测值,采用测方向三角网函数模型与测角网函数模型,进行了相应的平差计算,并对两种计算结果进行了比较分析。
测方向三角网;测角网;函数模型;间接平差
0 引言
如图所示,图1为测方向的三角网,图2为测角的三角网。A、B、C为已知坐标的三个控制点,加密待定点D,起算数据列于表1。以下分两种方式来解求待定点D的坐标,并给出精度。
方式一:采用测方向三角网函数模型
如图1,在四个测站上同精度测得10个方向,观测值列于表2,以D点坐标为平差参数,求D点坐标的平差值。
方式二:采用测角网函数模型
如图2,同精度测得6个角度,观测值列于表3,以D点坐标为平差参数,求D点坐标的平差值。

表1 起算数据
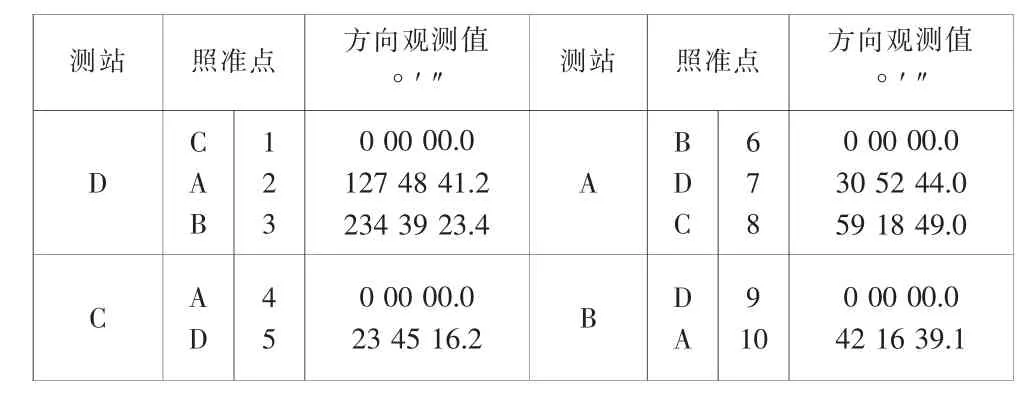
表2 方向观测值
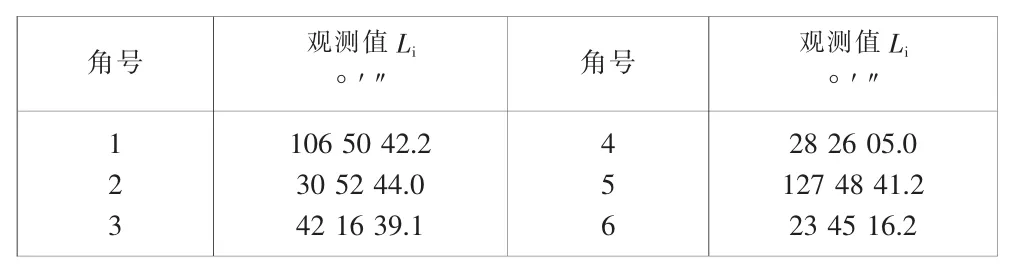
表3 角度观测值
在实际的测角工作中,初始的直接观测值是利用经纬仪或全站仪所测得的方向值。对于方式一,是以这些方向值为观测数据,进行三角网的平差;对于方式二,是以同一测站观测方向值做差而求得水平角,然后以这些水平角为观测数据,进行三角网的平差。
采用方式一,保留了原始数据的一些特征和信息;采用方式二,由于各方向值之间做差,从而消除了或减弱了初始直接观测值的一些信息,势必使得利用这两种方式所求的最终结果之间产生一些差别,从而对最终结果的精度产生影响。
本文通过对两种情况的解算,对计算结果进行了比较分析。
1 理论内容
1.1 测方向三角网函数模型
如图3所示为方向观测的示意图。
由于每一个测站有一个定向角,它们是方向坐标平差中的未知参数,设其平差值为则得误差方程
1.2 测角网函数模型
如图4所示为测角示意图。
对于观测角度Li,其误差方程
2 计算分析
2.1 方式一
该情况中,n=10,1个待定点,必要观测为1×2=2.另外再方向观测的情况下,还需确定4个测站定向角,故必要观测t=2+4=6.设参数为XD, YD,ZA,ZB,ZC,ZD,且D点坐标近似值为则误差方程的系数矩阵B和常数矩阵l

表4 各参数改正数所对应的系数和常数项
由于是同精度观测,从而进一步求解此误差方程,得参数的改正数为

表5 各改正数的计算结果
2.2 方式二
该情况下,n=6,t=2,则设D点坐标的平差值为参数,记为XD,YD,且D点坐标近似值为则
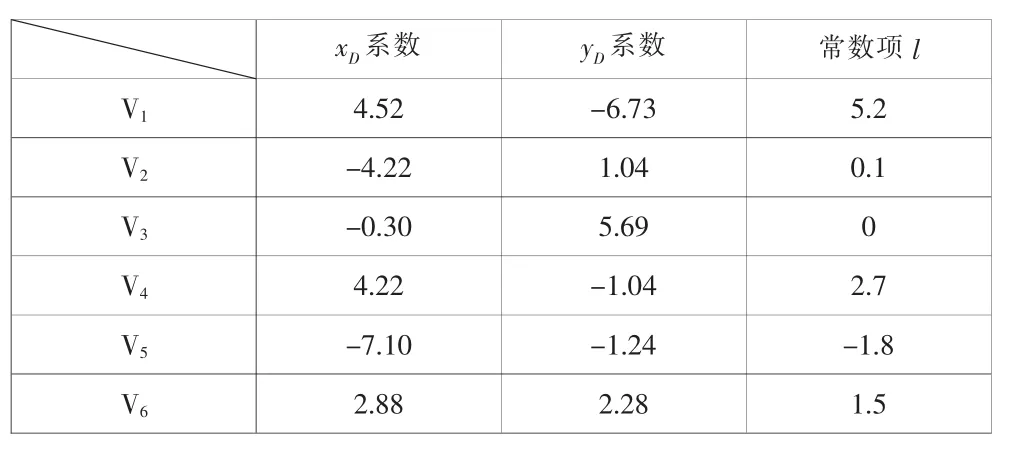
表6 误差方程中各参数改正数所对应的系数和常数项
由于是同精度观测,解此误差方程,得

表7 各改正数的计算结果
2.3 待定点D的坐标平差值及其坐标中误差

表8 两种方式下D点坐标平差值及其精度比较
3 结论
尽管二者的差别很小,但还是有区别的。差别的原因可能包括以下几点:
(1)解算过程中D点近似坐标的选取不同引起的误差;
(2)解算过程中非线性函数线性化时,将二次以上各项舍去时引起的误差等等;
(3)本次的解算是在经典平差范畴内进行的,由于忽略了观测值间的相关性等,从而引起误差。
为了提高计算结果的精度,可以尝试采取以下方法:
(1)根据精度需要,尝试进行二次平差或更高次的平差;
(2)解算时采用近代平差的思想进行,会更好地提高解算结果的精度。
[1]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础(第二版)[M].武汉大学出版社,2009.
[2]泥立丽,等.基于Excel的绘制误差曲线的方法[J].矿山测量,2010.
[3]王永,等.Excel应用于《误差理论与测量平差基础》辅助教学[J].中国科技信息,2012.
[4]翟学敏,等.Excel在高斯投影坐标正算公式中的应用[J].科技信息,2010.
[5]苗元欣.基于一元线性回归的变形监测数据处理与分析[J].山西建筑,2013.
[6]王永,等.利用Excel绘制误差椭圆的方法[J].矿山测量,2008.
[责任编辑:李书培]
王振(1978.08—),男,汉族,山东曹县人,本科,在山东省地质矿产勘查开发局第五地质大队工作,主要从事工程测绘、工程测量等方面的技术与管理工作。

