高速铁路斜拉桥二次调索计算分析
白先梅
(广东省建筑设计研究院, 广州 510010)
高速铁路斜拉桥二次调索计算分析
白先梅
(广东省建筑设计研究院, 广州 510010)
在斜拉桥施工过程中,由于各种因素的影响,使得实际的索力与理论计算的索力往往存在一定的偏差。为保证斜拉桥施工过程中桥梁受力安全和成桥状态索力达到设计的预期值,需要对斜拉桥的索力进行控制和调整。文章结合某高速铁路桥梁实际工程,根据影响矩阵原理建立数学模型进行二次调索模拟,并对斜拉索的施调索力进行计算,最终得出斜拉桥的合理成桥索力,施工时进行二次张拉。该方法在新建高速铁路斜拉桥的设计与施工中得到了具体应用。通过对索力的调整,可以显著消除实际索力值与理论值的偏差,在斜拉桥中建立起合理的内力和理想的线形。该方法也可应用于高速铁路运营阶段斜拉桥的索力偏差调整,为运营和养护提供了数据支持。
影响矩阵法; 斜拉桥; 二次调索; 索力控制
特殊结构和大跨度桥梁的建设是反映我国高速铁路桥梁建设水平的重要标志,受高速铁路运营对桥梁结构刚度和线路平顺性等要求的影响,对斜拉桥等柔性大跨度桥梁的受力和变形,均有非同于一般桥梁的要求。斜拉桥施工过程中,索力的控制是成桥线控制的重要方法,斜拉索索力和斜拉桥主梁线形受环境和施工因素影响较大,需要在施工过程中根据实际情况和设计要求进行调整[1]。因此,施工过程中要考虑各种因素的影响,制定合理的索力张拉,索力控制,索力调整方案,以达到设计成桥索力理论计算值和使用阶段拉索受力要求。二次调索在桥梁合龙后进行,通过二次调索使斜拉桥最终达到理想的成桥状态。
斜拉桥索力调整的计算方法有很多,目前常用的有最小二乘法[2]、弯矩最小法、弯曲能量法及基于影响矩阵原理的影响矩阵计算法[3]。最小二乘法的原理是通过迭代计算使误差的平方和最小。弯曲能量法和弯矩最小法在计算时要改变桥梁结构模式,以弯曲能量和弯矩平法和作为目标函数,使其达到最小值。基于影响矩阵原理的斜拉桥调索计算是将索力变量和其广义影响矩阵为目标函数,通过函数计算、优化等实现程序化计算[4]。
高速铁路斜拉桥与普通铁路、公路斜拉桥相比具有更高的要求,高速铁路桥梁必须具有高平顺性,以保证高速行驶的安全及旅客乘坐的舒适性,因此对桥梁的竖向、横向刚度及桥梁的线形有更高的要求。本文以某新建高速铁路的一座斜拉桥为例,根据影响矩阵计算原理,采用约束最优法[4],建立调索的模型,通过MADIS程序计算斜拉桥施加索力的调整值及调索过程中最终的索力控制值,为斜拉桥建设施工的二次调索提供技术保证。
1 二次调索的影响矩阵法
斜拉桥进行二次调索时,桥梁结构主体施工基本完成,此时拉索已有初始索力,初始索力记为Tc,进行二次调索时的目标索力记为Tm,按照一定的调索顺序,给每根斜拉索施加单位索力。然后计算单位索力作用下指定截面的应力、指定点的位移等量值的变化量,即得到各个物理量的影响矩阵[5]。
根据影响矩阵调索计算原理,计算出施工调索各阶段每束拉索索力施加调整量Ts,在保证结构安全的前提下,比较不同的调索顺序和索力调整值,选出最优的调索方案。二次调索结束后使索力值达到目标索力值[6]。
1.1 影响矩阵法原理
以双塔斜拉桥为计算模型,将斜拉索进行编号,如图1所示。以每束斜拉索的索力变化量作为调整向量说明影响矩阵的原理,如图2所示。
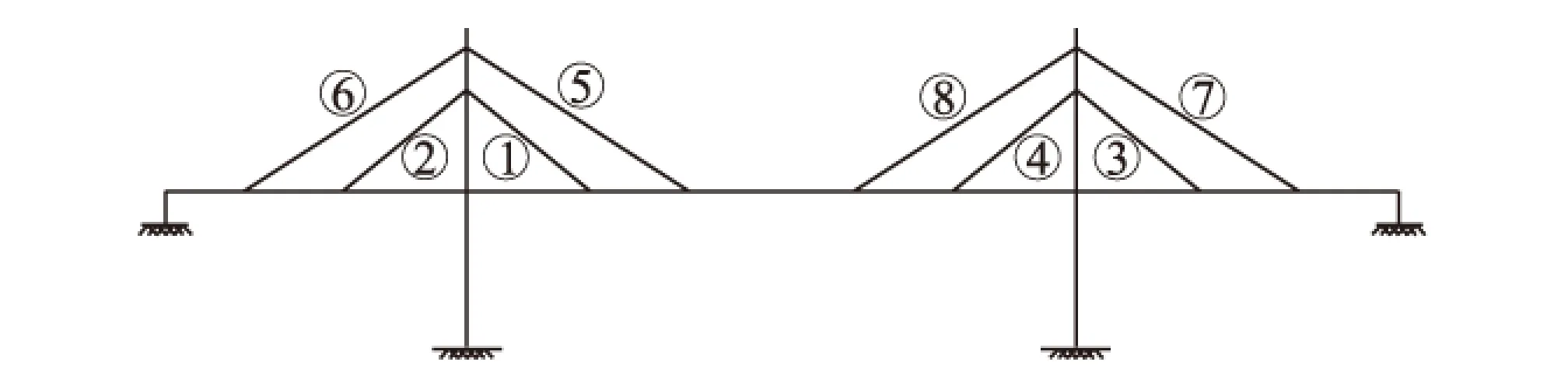
图1 双塔斜拉桥计算模型图
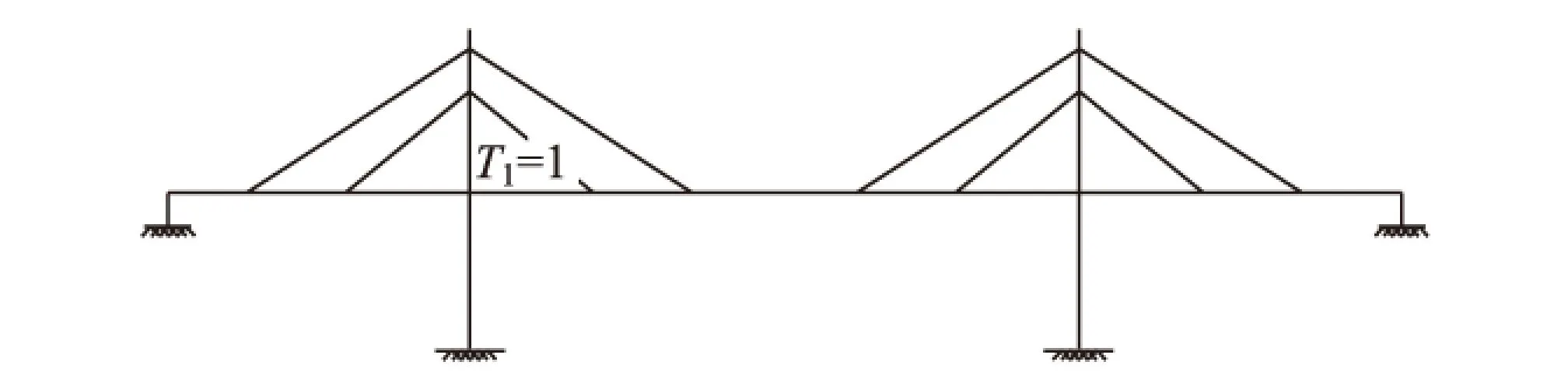
图2 双塔科拉桥影响结构图
在1号斜拉索上施加单位索力T1=1时, 1~8号斜拉索相应的索力会有变化,将增加量记为{Ti1}(i=1,2,3,4,5,6,7,8),同理,在j号斜拉索上施加单位索力Tj=1时, 将1~8号斜拉索的索力变化量,即增加量记为{Tij}(i,j=1,2,3,4,5,6,7,8)。因此可以得到索力调整的影响矩阵:
(1)
同理以位移为调整向量,根据布置的监测点可以得出所需监测点A1,A2,…,An的位移影响矩阵,以应力为调整向量,可以得到关于截面C1,C2,…,Cn的应力影响矩阵。分别记为MΔ,Mσ,其中:
(2)
Mσ的形式与MΔ相同。
1.2 二次调索最优控制的数学模型
斜拉桥二次调索的过程就是根据确定的调索顺序和索力调整值的大小,在满足内力、位移、索力的约束条件下,经过一系列中间状态最终达到目标状态。在二次调索前,桥梁结构的主桥施工已经完成,桥梁的结构体系已基本确定,斜拉索已经具备一个索力,将这个状态作为调索的初始状态,将此时的索力记为初始索力Tc、将控制截面的初始应力记为σc:
(3)
(4)
监测点在该状态下的标高作为初始标高,即初始位移Δc=0。
根据上述影响矩阵法计算原理计算斜拉桥索力的影响矩阵MT,是n×n阶矩阵,矩阵的元素用MTij表示,即在第j号索上施加单位力1时,i号斜拉索的索力变化值。斜拉索最终的目标索力值Tm,二次调索施加的索力向量为Ts,则:
Tm=Tc+MTTs
(5)
目标索力值即是设计计算的成桥索力,因此可以求出二次调索的调整向量Ts:
(6)
得到二次调索的施加调整量后,按照一定的调索顺序最终可以使全桥的索力达到目标索力。但在实际施工中要找到最优的调索顺序方案,还需考虑结构内力、应力、位移不能超过允许值,将这些作为约束条件,以保障结构的安全性。
根据二次调索阶段的最不利工况,列出约束条件:
(7)
计算时考虑应力在计算允许值范围内,使位移约束尽可能小,然后求解出最优调索顺序方程{x}={x1,x2,...,xn},则可建立单目标、多约束的系列方程式:
(8)
(i=1,2,3,…,n;k=1,2,3,…,n)
式中:Tmaxi——按照所有的调索顺序调整时i号索出现的最大索力值;
Tmi——第i号索的索力目标值;

Δ′——相邻的两截面位移差值的限制值;
(9)
式中:Ai——除对角线上第i个元素为l,其余元素均为0的系数矩阵;
Tcsi——调整第i根索时对所有拉索索力的影响值;
MCST——按n个列向量Tcsi排列组成的索力影响矩阵;

αij——矩阵MCST的第i行j列组成元素值;
Tzi——调第i根索时该索在当前调索阶段的索力最终控制值[7]。
求出Tzi后,则可得出在最优调索顺序下每根索在调索过程中的索力控制终值:
Tz={Tz1,Tz2,…,Tzn}T
(10)
2 工程实例
2.1 工程概况
该工程为四线高速铁路双塔双索面双主桁钢桁梁斜拉桥,设计列车时速为250km/h,预留300km/h的提速空间。斜拉桥主桥跨径布置为(57.5+109.25+230+109.25+57.5)m,钢桁梁采用带K撑的双主桁设计,桁间距24m,共48个钢桁梁节间,每个节间11.5m。斜拉索采用对称均匀布置,共36对斜拉索。如图3、图4所示。

图3 斜拉桥主桥示意图

图4 斜拉桥主桥立面图(m)
该桥在四线铁路桥梁中第一次采用双主桁钢桁梁斜拉桥结构,首次采用带水平K撑的宽桁桥面系及甲基丙烯酸甲酯(MMA)树脂道砟钢桥面防水防护技术。在我国高速铁路建设史上,双主桁双塔钢桁梁斜拉桥这种结构形式在国内尚属首次,构造及受力十分复杂,施工过程中桥梁结构截面应力分布、挠度变化、斜拉索索力和塔顶偏位都要处于安全合理的范围之内,因此索力控制尤其重要。
2.2 结果分析
该斜拉桥共36对斜拉索,因二次调索时两个塔的同组斜拉索能够同时对称张拉,故可对72根索的索力影响矩阵进行简化,M/S(0、1、2、3)这4组索的索力相互影响矩阵为:
将该桥在二期恒载施工完成后的索力值作为初始索力,将这个阶段的位移作为初始位移(假定为0),以索力为施调向量,成桥索力为调索目标,以成桥索力偏差±2%、塔顶位移±10mm为约束条件进行二次调索计算分析。通过约束最优方法得出二次调索的最优顺序:M0、S0、M1、S1、M2、S2、M3、S3,按照这个最优调索顺序,计算出该斜拉桥斜拉索索力施加调整值和索力控制的终值,如表1所示,二次索力调整前后索力对比,如图5所示。
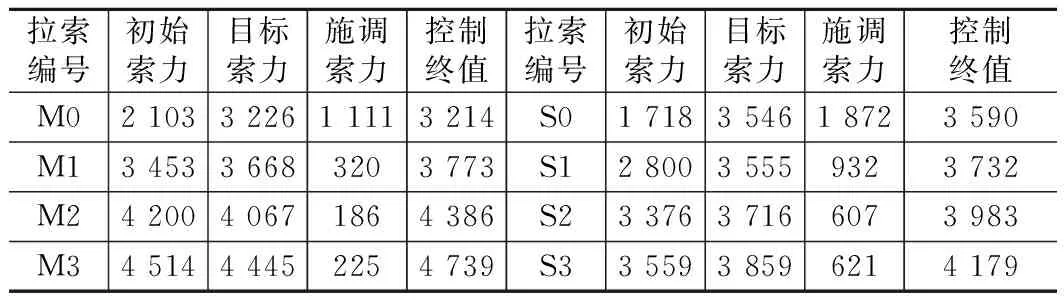
表1 特大桥斜拉索的施调索力和索力控制终值表(kN)
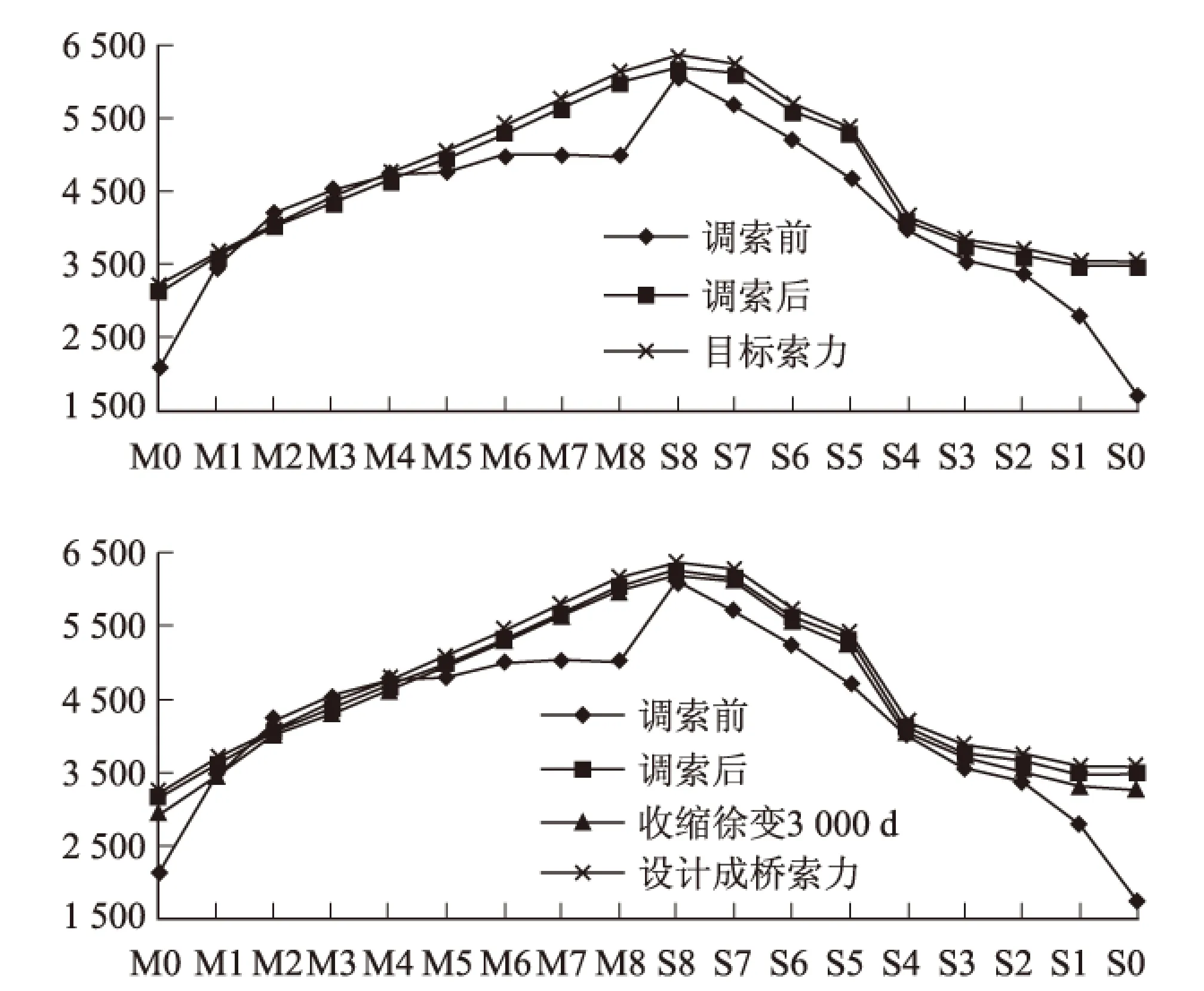
图5 斜拉桥二次调索前后索力对比图(kN)
从表1和图5可以看出,基于影响矩阵法的二次调索方法能在保证结构安全的前提下使得全桥索力达到目标值。
3 结束语
本文根据影响矩阵计算原理,通过程序计算建立斜拉桥二次调索施工控制的数学模型,并且利用惩罚函数中的约束最优法将单个目标、多个约束问题转化成没有约束问题进行求解。这种方法在计算时考虑了二次调索过程中的索力安全系数,主梁的结构内力,斜拉索内力及主梁拉索变形位移等约束条件,确保了调索过程中结构体系的安全。通过影响矩阵法计算进行二次调索,使全桥索力达到目标索力。在斜拉桥运营使用阶段由于各种因素影响使索力出现偏差时,也可用此方法来调整偏差。
[1] 周孟波.斜拉桥手册[M].北京:人民交通出版社,2004. ZHOU Mengbo. Cable stayed bridge manual [M].Beijing: China Communications Press,2004.
[2] 钟继卫.斜拉桥合拢后索力最优调整的实现[J].世界桥梁,2002,30(4):43-44. ZHONG Jiwei. Optimum adjustment of the cable force of cable-tayed bridge[J].Foreign Bridges,2002,30(4):43-44.
[3] 肖汝诚,项海帆.斜拉桥索力优化的影响矩阵法[J].同济大学学报(自然科学版),1998,26(3):235-240. XIAO Rucheng,XIANG Haifan. Influence matrix method of cable force optimization of cable stayed bridge[J]. Journal of Tongji University(Natural Science),1998,26(3):235-240.
[4] 杜蓬娟,张哲,黄才良.斜拉桥成桥后误差调整的优化方法[J].哈尔滨工业大学学报,2005,37(7):1016-1018. DU Pengjuan,ZHANG Zhe, HUANG Cailiang. Optimization method of error adjustment after completion of bridge[J].Journal of Harbin Institute of Technology,2005,37(7):1016-1018.
[5] 梁鹏,肖汝诚,张雪松.斜拉桥索力优化实用方法[J].同济大学学报(自然科学版),2003,31(11):1270-1274. LIANG Peng,XIAO Rucheng, ZHANG Xuesong. Practical method for cable force optimization of cable stayed bridge[J].Journal of Tongji University(Natural Science). 2003 ,31(11):1270-1274.
[6] 伍华成,汪劲丰,项贻强.基于优化索力的斜拉桥索力状态评估研究[J].浙江大学学报(工学版),2006,40(10):1773-1777. WU Huacheng, WANG Jinfeng, XIANG Yiqiang. Research on cable force state evaluation of cable stayed bridge based on optimized cable force[J]. Journal of Zhejiang University(Engineering Science),2006,40(10):1773-1777.
[7] 雷丽恒.斜拉桥索力优化设计探索[J].中外公路,2006,26(6):77-80. LEI Liheng.Study on cable force optimization design of cable stayed bridge[J].Journal of China & Foreign Highway, 2006,26(6):77-80.
[8] 林元培.斜拉桥[M].北京:人民交通出版社,1994. LIN Yuanpei. Cable stayed bridge [M]. Beijing:China Communications Press,1994.
Calculation and Analysis of Secondary Adjustment of Cable Force of High-speed Railway Cable-stayed Bridge
BAI Xianmei
(Architectural Design and Research Institute of Guangdong Province, Guangzhou 510010, China)
During the construction process of cable-stayed bridge, due to various factors, the actual value and theoretical calculation of cable force often have a certain bias. To ensure the security of bridge force during the construction of cable-stayed bridge and the cable force of bridge status can achieve the desired design value, there is a need to control and adjust the cable force of cable-stayed bridge. Combined with the practical engineering of a high-speed railway bridge, mathematical model is established to simulatet the secondary adjustment of the cable force based on the principles of impact matrix, and the adjusted cable force of stay cable is calculated, which is applied to calculate the reasonable cable force finally, and secondary tension is conducted when construction. This method has been applied to the design and construction of new high-speed railway cable-stayed bridge. Through the adjustment of cable force, we can significantly eliminate the deviation between the actual value and theoretical value of cable force, and establish a reasonable internal force and an ideal linear of cable-stayed bridge. The method can also be applied to the offset adjustment of cable force of cable-stayed bridge during the high-speed railway operational phase, and provide data support for the operation and maintenance.
impact matrix method; cable-stayed bridge; secondary adjustment of cable force; cable force control
2016-03-16
白先梅(1982-),女,工程师。
1674—8247(2016)04—0046—04
U448.27
A

