基于粒子群算法的地铁列车节能运行优化
梁 枫,秦 斌,王 欣,张 凯,曹成琦
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
基于粒子群算法的地铁列车节能运行优化
梁 枫,秦 斌,王 欣,张 凯,曹成琦
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
针对降低轨道交通运行能耗的问题,提出基于粒子群算法的地铁列车节能运行两阶段双层优化方法。首先依据列车行车组织的特点,建立列车运行调整模型,在第一阶段利用粒子群算法全面搜索列车最优节能驾驶曲线,即在符合运行时间约束的前提下获得最优运行曲线;第二阶段为时刻表运行时间优化,利用第一阶段所获得的优化结果,生成各区间的能耗-时间曲线,进而优化列车时刻表。采用某地铁2号线数据对此方法进行测试。测试结果表明:本优化算法对实际线路中列车的节能运行以及时刻表的制定与优化具有良好效果。
粒子群算法;地铁;节能优化
0 引言
随着我国经济的飞速发展以及城镇化的大力推进,地铁已经越来越多的应用到城市中[1]。地铁列车的牵引能耗占总能耗的50%,因此降低轨道交通运行能耗成为了城市可持续发展的目标之一。列车在运行过程中会频繁的启动和制动,这会消耗较大的能量。因此,如何在保证准点和舒适的前提下,利用列车节能目标速度曲线以指导列车运行、降低列车能耗成为重要的研究课题。
国内外学者对城市轨道交通列车节能运行进行了研究。南澳大学SCG(Scheduling Control Group)研究所P. G. Howlett等[2]提出了列车节能运行的能耗模型,并在此基础上建立列车运动方程,进行节能优化策略的研究;S. Yasunobu[3]提出了地铁列车运行的模糊预测控制方法,对单列车运行过程进行优化,以达到节能效果,但模糊预测控制方法列车运行过程中存在的多目标问题;付印平等[4]对列车节能操纵优化方法展开研究,通过仿真计算,搜寻节能设置方案,而对于列车具体运行过程未作考虑;石红国[5]运用遗传算法对列车运行过程进行优化,得到优化运行时间,但遗传算法的局部搜索能力较弱,而且有早熟收敛现象;Chen J. F.等[6]通过优化列车停站时间来降低地铁运输系统能耗峰值,但停车时间的不确定性以及人流量等其他因素会影响控制效果;Wong K. K.等[7]应用动态规划方法对地铁列车的站间运行时间与站点停站时间进行优化,得到优化时间方案,而动态规划算法没有统一的标准模型,它的数值方法求解存在维数灾;R. Chevrier等[8]采用优化铁路时刻表来节约能源,求解模型节能效果较好,但各种工况以及实际运行过程未作考虑,对于定时策略下的模型适用性不强。
在以往的研究中,大多将列车节能控制优化和列车运行时间优化看作2个独立的过程。实际上,列车运行控制方案是以运行时间为前提进行优化设计。不同的运行时间会使列车运行能耗不同。因此,本文利用粒子群优化算法对列车运行速度曲线和停站时间修正量表进行优化,以达到节能目的。
1 列车节能运行的优化模型
1.1 列车工况速度的优化模型
根据列车的运行工况转换规则,并结合实际运行情况,初步制定部分工况转换的约束条件,并生成工况序列表。
1)列车启动出站为牵引,停车进站为制动。
2)牵引后只能为惰行,制动后为停车或惰行。
3)牵引时,根据列车自身牵引电机的特性,施加最大牵引力进行牵引。
4)制动时,列车以恒加速度进行制动。
以2次惰行运行为例,列车站间运行工况及控制如图1所示。
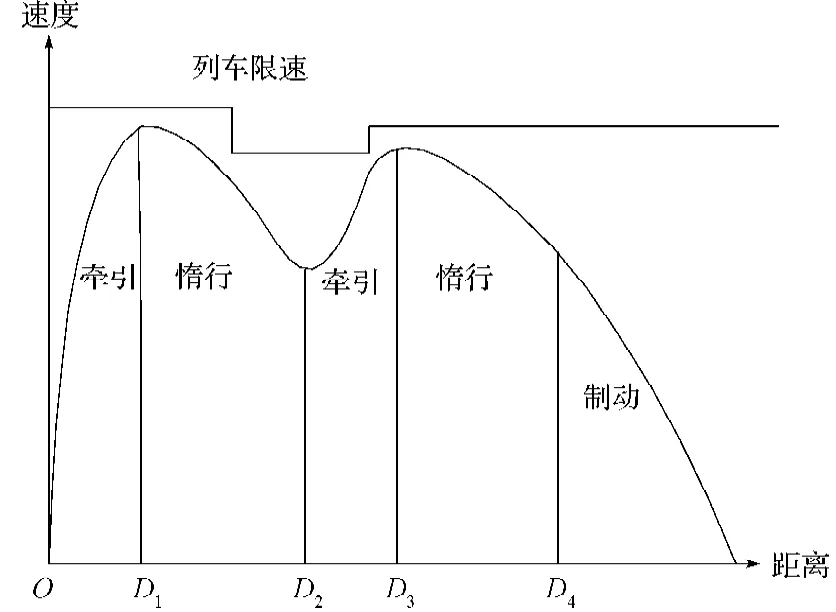
图1 2次惰行过程的列车运行曲线Fig.1 Train operation curves in two coasting processes
图1中,D1,D2,D3,D4为工况转换点。0~D1是列车启动;D1~D2是列车惰行运行;D2~D3是列车再次牵引;D3~D4是列车再次惰行;从D4后,列车开始制动,直到停车。列车选择工况运行的目标是在其他条件正常不变的情况下,实现列车能耗最小。优化模型的目标函数可以描述为

式中:a为列车运行时间的权重;Ti为区间i时刻表要求的列车运行时间,单位为s;Ts为优化后列车实际运行总时间,单位为s;d为列车运行晚点的惩罚因子;b为列车运行能耗的权重;E(Ti)为列车实际运行能耗,单位为kW·h;Es为优化后列车运行能耗,单位为kW·h;c为列车运行距离的权重;Si为站间的列车运行实际距离,单位为m;Ss为优化后的列车运行距离,单位为m;e为列车运行距离的惩罚因子。a,b和c的取值根据计算原则而设定,取决于对运行时间、运行能耗和运行距离的取舍。根据相关文献,a+b+c=1,a=0.3,b=0.4,c=0.3。
列车工况速度的优化模型约束条件如下。
1)列车站间实际运行时间Ts不能大于给定标准时间Ti,即

2)列车首次进行惰行运行必须遵守的约束为

式中:D1为第一次惰行开始的位置;Dcoast为列车从启动到开始惰行的最短距离。
3)列车惰行转换点的位置约束为

式中Dj为第j个工况转换点。
4)运行过程中,列车的速度不能超过最大速度。
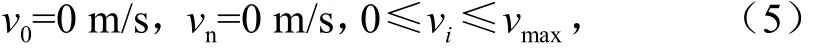
式中:v0为列车运行的初始速度;vn为列车运行的末速度;vi为列车当前运行速度;vmax为列车运行的最大速度。
5)列车运行过程中的加速度为
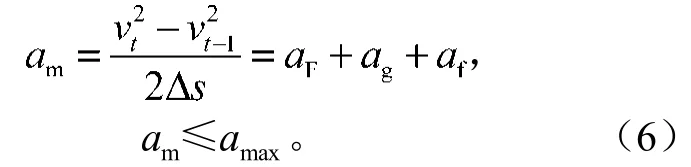
式中:Δs为列车运行的距离;vt为t时刻的列车运行速度;vt-1为t-1时刻的列车运行速度;aF为机车牵引力产生的加速度;ag为坡度阻力产生的加速度,它由运行线路的坡度决定;af为基本阻力产生的加速度,它由列车当前运行速度决定;amax为列车的最大加速度。参考列车运营相关参数设定,列车启动的最大加速度为1 m/s2,制动的最大加速度为-1 m/s2。
1.2 列车运行时间优化模型
为了获得更好的节能效果,本课题组在研究列车节能运行策略的同时,也将时刻表的优化问题进行考虑。
列车的运行能耗最小目标函数为

式中:E(Tj)为列车运行区间的总能耗,单位为kW·h;Tj为第j辆列车运行的时间。
列车运行时间优化模型的约束条件如下。
1)对于客流量较大的站,停站时间只增不减;
2)列车运行周期的时间变化限定在[-12, 12]之间,单位为s;
3)同一时刻,进站列车反馈的能耗被出站列车牵引利用。
2 基于粒子群算法节能优化
粒子群优化算法(particle swarm optimization,PSO)具有较好的收敛速度和寻优精度,较强的搜索速度和搜索能力,因此,本课题组在Matlab软件中构建了一个双层模型,并利用粒子群优化算法进行优化[9]。
2.1 粒子群优化算法
粒子群优化算法是进化计算技术的一种,它最早由国外的2位学者J. Kennedy与R. C. Eberhart于1995年提出。粒子群优化算法是通过调整粒子的速度和位置来实现信息的交换与共享[10]。初始时,先随机产生一组随机解,通过多次迭代后,搜寻最优解。
粒子群优化算法的流程如下。
1)算法初始化。初始化n个粒子,随机产生n个初始解以及n个初始速度。
2)求解每个粒子的适应值,然后根据当前位置和速度产生新个体。
3)计算新个体的适应值,若新的适应值优于原来的个体极值Pbestk,则更新Pbestk。
4)在本次迭代中,找到种群的全局最优解gbestk。
5)跳转至步骤2,直到满足求解的适应值,算法结束。
2.2 列车运行工况转换点优化
列车运行工况的转换点,即Dj是模型的特征变量,每个转换点的位置对应一个维度变量参数。初始种群按照列车运行距离的递增生成,必须满足式(4)。
2.3 列车站间运行时间优化
在一组区段内,将列车在所有站点的停站时间看成一个矩阵,各个站台列车的停车时间增量表可以用适应度向量Xi(i=1, 2, ...,n)表示。因此求解适应度向量Xi的最优值就可以求得最优时刻表。
PSO算法流程如图2所示。
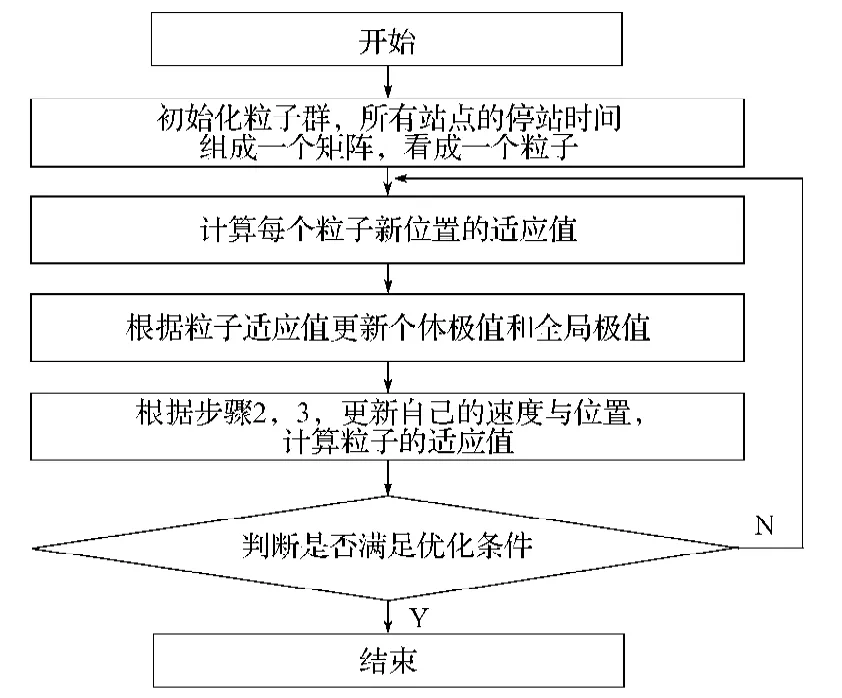
图2 PSO算法流程图Fig.2 PSO flow chart
3 仿真测试及结果对比
3.1 单列车仿真模型
电力系统模块(power system block,PSB)是Matlab/Simulink中的仿真软件包模块,可用于电力系统和电力电子装置以及电力驱动等的仿真。
地铁牵引供电系统中,PSB模型的组成如下。
1)24脉波整流模块。牵引变电站将33 kV三相交流电压经24脉波整流,形成1 500 V直流电压,为列车供电[11]。
2)直流接触网模块。电网中的阻值参数随着运行时间(运行距离)的变化而变化。
3)DC-AC逆变器[12]。将直流电逆变成交流电,使之产生一个与电机频率相同的电压,供电机运行。
4)DTC控制器。控制异步电机的磁链和转速。
列车在一个站间的速度运行曲线如图3所示。
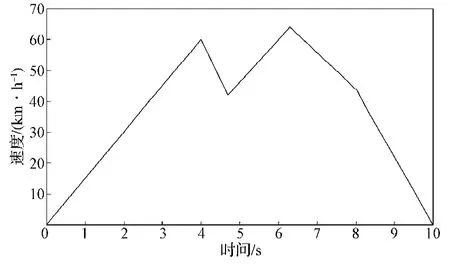
图3 列车站间速度运行曲线Fig. 3 Speed running curve of train stations
由图3可知:在0~4.0 s,列车为牵引阶段,电机通过消耗能量运行,列车匀加速运行;在4.0~4.7 s,列车为惰行阶段,列车不消耗能量,惯性运行,在阻力作用下,列车减速运行;在4.7~6.3 s,列车为再牵引阶段;在6.3~8.0 s,列车为再惰行阶段;在8.0~10.0 s,列车为制动阶段,直到列车停车即减速到0 m/s2。
3.2 多列车仿真模型
以武汉地铁2号线为例,该线路实际有26辆列车,共21个站。本课题组将仿真测试作如下简化:将列车等效为一个电流源;列车启动牵引加速运行时,列车吸收电网电能;列车停车制动减速运行时,列车反馈电网电能;列车惰性运行时,列车既不吸收电网电能也不反馈电网电能,相当于与电网断开。故本课题组利用通断开关将电流源与电网断开就能实现上述过程[13]。
3.3 PSO算法优化结果
3.3.1 列车速度曲线优化
取武汉地铁2号线从中山公园到循礼门站,全长1 533.8 m,运行时间110 s,能耗30.4 kW·h。时刻表中给定时间为120 s,冗余的10 s为实施惰性运行提供空间。一般情况下较多的惰性运行会导致运行时间延长,但可以节能,因此,充分利用冗余的10 s。
利用PSO算法对偶数个工况转换点(即维度为4, 6, 8)进行优化搜索,迭代20次,得到区间能耗数据[14]如图4所示。由图可知,第一个阶段,在维度8即8个工况转换点下进行优化时,运行时间超过了时刻表中规定的时间,故列车不能在规定的时间内到达;在维度6即6个工况转换点下进行优化时,列车的运行速度曲线最优,能耗最小。
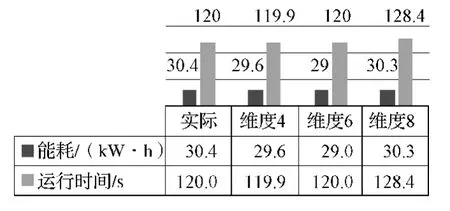
图4 不同维度下的能耗和时间Fig. 4 Energy consumption and execution time in different dimensions
3.3.2 列车运行时间优化
模型由5辆车并联,6个站台组成,则可形成一个6×5的时间分配矩阵,一共30个元素。每个元素表示一辆列车在一个站台的停站时间修正量,取值范围为[-5, 5],单位为s。利用PSO算法时,将该矩阵看成一组解。初始矩阵为

经PSO算法优化,迭代20次,迭代次数-适应值的响应曲线如图5所示。

图5 PSO算法优化响应曲线Fig. 5 An optimization response curve of PSO
经过20次迭代后,得到优化后的新矩阵

将优化后的停站时间方案加入地铁仿真中运行,得到优化前后的能耗对比如图6所示。由图可知,使用PSO算法优化后的能耗较优化前有所降低。

图6 优化前后能耗对比图Fig. 6 A comparison chart of energy consumption before and after optimization
总的来说,PSO优化算法在两个阶段都降低了能耗,达到了节能的目的。
4 结语
本文利用PSO算法对地铁列车进行2个阶段的优化。第一个阶段,通过改变列车工况转换点的个数来进一步改善列车的运行状况,在其他条件正常情况下运行,可以降低列车的能耗。第二个阶段,通过优化列车的停站时间修正表,来改变每辆列车在每个站点的停站时间,使同一时间能有更多的列车同时进出站,从而达到节能的目的。
本文的两个阶段的优化,可以使列车的速度和运行控制得到有效的结合,可以有效的降低能耗。列车在实际运行中,受列车运行的线路、复杂的工况以及人流量等因素的影响,PSO算法优化更加复杂。所以,在实际中如何进行优化调整需要进一步研究。
[1]WANG Zijia,CHEN Feng,SHI Zhongheng. Prediction on Medium and Long-Term Energy Consumption of Urban Rail Transit Network in Beijing[J]. China Railway Science,2013,34(3):133-136.
[2]HOWLETT P G,MILROY I P,PUDNEY P J. Energy-Efficient Train Control[M]. [S. l.]:Springer,1994:193-200.
[3]YASUNOBU S. Application of Predictive Fuzzy Control to Automatic Train Operation Controller[C]//Proceeding of Industrial Electronics Control and Instrumentation. Tokyo:[s. n.],1984:657-662.
[4]付印平,高自友,李克平. 路网中的列车节能操纵优化方法研究[J]. 交通运输系统工程与信息,2009,9(4):90-96. FU Yinping,GAO Ziyou,LI Keping. Optimization Method of Energy Saving Train Operation for Railway Network[J]. Journal of Transportation Systems Engineering and Information Technology,2009,9(4):90-96.
[5]石红国. 列车运行过程仿真及优化研究[D]. 成都:西南交通大学,2006. SHI Hongguo. Study on Train Operation and Movement Process Simulation and Its Optimization[D]. Chendu:Southwest Jiaotong University,2006.
[6]CHEN J F,LIN R L,LIU Y C. Optimization of an MRT Train Schedule:Reducing Maximum Traction Power by Using Genetic Algorithms[J]. IEEE Transactions on Power Systems,2005,20(3):1366-1372.
[7]WONG K K,HO T K. Coast Control for Mass Rapid Transit Railways with Searching Methods[J]. IEE Proceedings-Electric Power Applications,2004,151(3):365-376.
[8]CHEVRIER R,PELLEGRINI P,RODRIGUEZ J. Energy Saving in Railway Timetabling:A Bi-Objective Evolutionary Approach for Computing Alternative Running Times[J]. Transportation Research Part C:Emerging Technologies,2013,37(3):20-41.
[9]雷开友. 粒子群算法及其应用研究[D]. 成都:西南大学,2006. LEI Kaiyou. Research on Particle Swarm Optimization and Its Application[D]. Chendu:Southwest University,2006.
[10]胡志超,凌 云. 基于粒子群优化的多弧离子镀膜温度控制模糊系统[J]. 湖南工业大学学报,2011,25(5):74-79. HU Zhichao,LING Yun.The Multi-Arc Ion Plating Temperature Control Fuzzy System Based on the Particle Swarm Optimization[J]. Journal of Hunan University of Technology,2011,25(5):74-79.
[11]史晓非,张 忠,贾洪成. 用MATLAB仿真异步电机直接转矩控制系统[J]. 大连铁道学院学报,2000,21(3):84-88. SHI Xiaofei,ZHANG Zhong,JIA Hongcheng. Using MATLAB to Simulate the Direct Self-Control System of Induction Motor[J]. Journal of Dalian Railway Institute,2000,21(3):84-88.
[12]吴晓东,关 强,李 冰. 基于VC、Matlab的汽车制动性能联合仿真[J]. 微计算机信息,2007,23(34):195-197. WU Xiaodong,GUAN Qiang,LI Bing. Combined Simulation of the Vehicle’s Braking Performance Based on VC,Matlab[J]. Microcomputer Information,2007,23 (34):195-197.
[14]毛明平,陶生桂,王曰凡. 上海地铁2号线牵引仿真计算研究[J]. 城市轨道交通研究,2001(2):22-27. MAO Mingping,TAO Shenggui,WANG Yuefan. Digital Simulation Calculation Method in Vehicle Traction of Shanghai Metro Line 2[J]. Urban Mass Transit,2001(2):22-27.
(责任编辑:邓 彬)
Optimization of Energy Saving Operation for Metro Trains Based on Particle Swarm Optimization
LIANG Feng,QIN Bin,WANG Xin,ZHANG Kai,CAO Chengqi
(School of Electrical and Information Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
With an aim to reduce the energy consumption in rail transit system, an optimized bi-level two-phase method has thus been put forward to achieve an energy saving operation for metro trains based on Particle Swarm Optimization. A new model for train operation adjustment has been established based on an analysis of the characteristics of train operation organization. In the first phase, Particle Swarm Optimization (PSO) has been used to comprehensively search the energy-saving operation curves of metro trains, thus obtaining the optimum operation curve under the premise of accordant running time constraints. In the second phase, the energy consumption-time curve for each interval is to be generated based on the optimization results produced in the first phase so as to further optimize the train schedule. The model has been simulated by using the data of a Metro Line 2. Experimental results show that the improved algorithm outperforms the traditional algorithm in that it presents a better effect on energy-saving operation and the formulation and optimization of time table in actual train lines.
particle swarm optimization (PSO); metro train;energy saving optimization
U260.13
A
1673-9833(2016)06-0029-05
10.3969/j.issn.1673-9833.2016.06.006
2016-10-09
国家自然科学基金资助项目(61673166),湖南省科技计划基金资助重点项目(2014FJ2018),湖南省教育厅科研基金资助重点项目(15A050),湖南省高校科技创新团队、湖南省研究生创新基金资助项目(CX2015B564)
梁 枫(1992-),男,湖北咸宁人,湖南工业大学硕士生,主要研究方向为电力系统及其自动化,E-mail :506262961@qq.com
秦 斌(1963-),男,湖南永州人,湖南工业大学教授,博士,主要从事复杂工业过程控制,机器学习方面的研究,E-mail :qinbin99@163.com

