Einstein双曲几何流方程Cauchy问题的整体解

朱晓睿

（公安海警学院 训练部，浙江 宁波 315801）

Einstein双曲几何流方程Cauchy问题的整体解

朱晓睿

（公安海警学院 训练部，浙江 宁波 315801）

本文中我们研究了一类定义在n维黎曼流形上的双曲几何流，并证明了小初值情况下的Cauchy问题的光滑解随时间整体存在。当变量t趋向于无穷时，由几何流方程的解所决定的度量的数量曲率趋向于0。该结论表明这类特殊的黎曼度量可以流成平坦度量。换而言之，具有适当初始度量的黎曼流形在双曲几何流下演化成欧氏空间。

双曲几何流；黎曼流形；非线性波动方程；整体解

一、引言

双曲几何流最早由刘克峰和孔德兴提出[3]，其局部光滑解和非线性平凡解的稳定性已被戴文荣、孔德兴和刘克峰所证明[1]。双曲几何流类比Hamilton提出的Ricci流的概念[2]，是一种新的有效工具用来研究流形的特性、时空中的奇点，以及其他微分几何和广义相对论中的问题。双曲几何流是一个非线性双曲偏微分方程系统。该几何流能帮我们很自然地理解波现象，并且得到关于Einstein方程许多有趣的结论。本文对于小初值的双曲几何流方程证明了解的整体存在性,并得到当t趋于无穷时，度量演化成平坦度量。

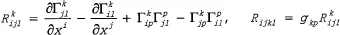
Ricci曲率可以由

得到,数量曲率可以由

得到。

双曲几何流方程由下式定义

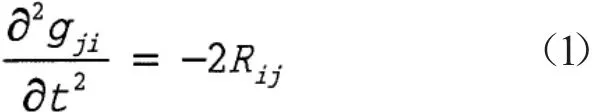
受到Einstein真空方程的启发，孔德兴和刘克峰引入了如下的双曲几何流方程，我们称为Einstein双曲几何流

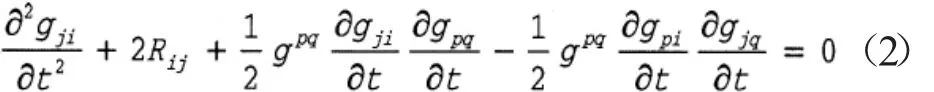
本文中，我们研究了具有如下初始度量的Einstein双曲几何流的发展方程

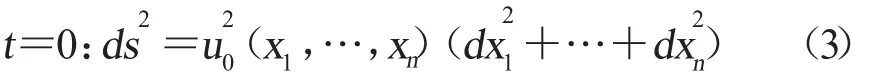
对于某些小初值的假设，我们证明了方程光滑解的整体存在,并且曲率随t趋向于无穷时趋于0。这说明了黎曼流形在双曲几何流下，当t趋向于无穷时趋于平坦流形。

本文由以下几部分组成。主要定理的叙述和证明在第二节，关于问题的扩展在第三节。

二、主要定理的证明

我们考虑如下Cauchy问题

我们将利用[4]中的结论来证明主要定理。

定理1 Einstein双曲几何流方程

的Cauchy问题对于所有时间t存在整体光滑解。而且由解度量决定的数量曲率随时间t趋向于无穷而趋于0。

证明：如果流形与欧氏空间共形，在共形变换下数量曲率变换公式如下(这里是欧氏度量):

利用以上记号，我们将（2）改写成

特别的，当n＝2时，方程变成

由于方程中不含有耗散项，我们直接讨论n＝3的情况。

我们做变换v＝u2，则

再做变换p＝logv，我们有

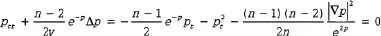
当t＝0，p＝εφ(x)，pt＝εφ(x)时，我们设＝2ln c，

由Taylor展开，我们有

由[4]中结论可知，定理成立。

三、关于定理的一些讨论和扩展

与其他广义相对论中的方程有诸多限制不同，双曲几何流不需要附加任何的限制条件。对于双曲几何流的Cauchy问题,我们需要两个初始条件来求解：一个是，另一个是。由于时间轴和其他坐标轴正交，因此这是一个可定系统。这是双曲几何流的一类新的主要特征。许多数学家致力于一些几何波方程的Cauchy问题。这类几何波方程是二阶偏微分方程，是积分算子作用在调和映射上的Euler-Lagrange方程，对所有的时间解都存在。并且可以得到一些有趣的估计。另一方面，双曲几何流由流形上的一族黎曼度量决定的Ricci曲率所决定。也就是说，双曲几何流具有的内蕴几何结构可以用来描述波算子的度量和曲率。这与调和映射问题有本质上的不同。由于我们可以通过波方程的核来理解热核，也就是说我们可以通过研究双曲几何流来得到关于Ricci流的一些新的性质，尤其是关于双曲几何流的奇点问题。

[1]Wenrong Dai,De-Xing Kong and Kefeng Liu, Hyperbolic geometric flow （I）:short-time existence and nonlinear stability,http://arxiv.org/abs/math/0610256.

[2]R.Hamilton,Three-manifolds with positive Ricci curvature[J].J.DifferentialGeom.17,1982：255-306.

[3]De-Xing Kong and Kefeng Liu,Wave character of metrics and hyperbolic geometric flow,http://www.cms.zju. edu.cn/UploadFiles/AttachFiles/200682885946597.pdf.

[4]Yachun Li,Classicalsolutionsto fully nonlinear wave equations with dissipation[J].Chinese J.Contemp. Math（17）1996：253-268.

The Global Solutions to Cauchy Problem in Einstein Hyperbolic Geometric Flow Equation

ZHU Xiaorui
（China Maritime Police Academy,Ningbo 315801,China）

In thispaper,we study thehyperbolic geometric flow which defined on the ndimensional Riemannian manifold,and proved the global smooth solution of the small initial value of the Cauchy problem.When it goes to the infinity,the scalar curvature determined by the geometric equation goes to 0.This conclusion shows that this special Riemannian metric evolved to the flat metric.In other words,If we choose the properly initial metric for the Riemannian manifold,it will evolve to the Euclidean space.

Hyperbolic geometric flow;Riemannian manifold;nonlinearwave equation;global solution

O175

A

2095-2384（2016）03-0053-03

（责任编辑 穆 静）

2016-08-25

本文得到浙江省自然科学基金项目资助（Q14A010002）。

朱晓睿（1981-），男，浙江宁波人，公安海警学院训练部副教授、博士，主要从事几何分析、理论物理等方面的研究工作。