软土盾构隧道施工阶段上浮量预测综述

王道远，朱永全，何　川

(1.西南交通大学土木工程学院，成都　610031；2.河北交通职业技术学院土木工程系，石家庄　050091；3.石家庄铁道大学土木工程学院，石家庄　050043)



软土盾构隧道施工阶段上浮量预测综述

王道远1，2，3，朱永全1，3，何川1

(1.西南交通大学土木工程学院，成都610031；2.河北交通职业技术学院土木工程系，石家庄050091；3.石家庄铁道大学土木工程学院，石家庄050043)

摘要：随着我国各大城市地铁和江河海底盾构隧道的兴建，施工过程中管片上浮问题已成为当前亟待解决的关键技术问题。首先，从上浮作用机理、横纵向刚度联系、上浮力分布规律以及上浮计算模型方面综述国内外研究现状及存在的问题。其次，在已有研究成果基础上，提出可进一步研究的思路和方向。主要包括：(1)将浆液充填、渗透视为连续过程，探求浆液黏度时变性下管片上浮力分布规律和计算公式；(2)摒弃了传统等效刚度模型和“梁-弹簧”模型，提出横、纵向折中的“局部刚度修正梁-梁”模型；(3)指出弹性地基圆梁法和修正惯用法不适用于分析盾构隧道施工阶段上浮问题，提出抗力反转局部上浮计算模型；(4)考虑浆液时变性、地应力、上浮力以及上覆地层反向压缩特性等因素，创建基于等效刚度或“局部刚度修正梁-梁”思想的盾构隧道整体上浮计算模型。最后，对如何实现给出相应建议。

关键词：盾构隧道；施工阶段；管片；上浮；预测

1概述

近年来，盾构法凭借其安全、可靠、快速、环保等优势广泛用于各大城市地铁、江河海底隧道等实际工程，以北京、上海、南京、广州和天津为例，在市区内地铁区间盾构约占70%以上，更有专家提出地铁全线采用盾构法开挖，然后在盾构基础上扩挖车站的构想[1]。然而，在盾构隧道施工中，刚脱离盾尾的管片经常会出现局部或整体上浮，表现为管片错台、裂缝、破损，乃至轴线偏位、管段渗漏等[2]。作为常见工程问题，盾构隧道施工中的管片上浮问题已经引起了广泛关注。目前隧道工程界主要采用弹性地基圆环法(美国)、全周弹簧法或Muir Wood法(英国、法国、德国、澳大利亚、奥地利)、考虑地层结构相互作用的Buqera法(西班牙)、修正惯用法或均质圆环法或梁-弹簧(日本)、弹性地基圆环法或自由变形圆环法(中国)进行盾构隧道设计[3-4]，基本上已可满足正常段盾构工程设计和施工的要求。相比之下，由于对盾构隧道施工阶段上浮机理和规律等认识不够，盾构施工过程上浮问题已成为当前亟待解决的关键技术问题。

首先，从上浮作用机理、横纵向刚度联系、上浮力分布规律以及上浮计算模型方面综述了国内外研究现状及存在的问题。其次，在已有研究成果基础上，提出了可进一步研究的思路和方向。主要包括：(1)将浆液充填、渗透视为连续过程，探求浆液黏度时变性下管片上浮力分布规律和计算公式；(2)摒弃了传统等效刚度模型和“梁-弹簧”模型，提出了横、纵向折中的“局部刚度修正梁-梁”模型；(3)指出弹性地基圆梁法和修正惯用法不适用于分析盾构隧道施工阶段上浮问题，并提出了抗力反转局部上浮修正模型；(4)考虑浆液时变性、地应力、上浮力以及上覆地层反向压缩特性等因素，创建了基于等效刚度或“局部刚度修正梁-梁”思想的盾构隧道整体上浮计算模型。最后，对如何实现给出相应建议。

2国内外研究现状及存在的问题

研究盾构隧道横、纵向上浮量预测问题，需深入研究以下几个问题：(1)上浮作用机理；(2)盾构横、纵向刚度计算方法；(3)横、纵向上浮力分布及大小规律；(4)横、纵向上浮计算模型。

2.1　上浮机理

根据已有大量城市地铁、江河海底盾构隧道实例来看，当管片脱离盾尾后，由于管片在盾构掘进和壁后注浆等复杂因素作用下，失去抗浮能力必将产生上浮。监测资料表明：标准断面的盾构隧道上浮一般在0～6 cm，但部分盾构管片上浮超过10 cm或者更多，致使侵入隧道限界，更为严重者需要调整线路来解决问题[5-6]。有关上浮作用机理，国内外众多工程师和学者从不同角度做了深入分析和研究。Lo[7]和姜忻良[8]认为盾尾与围岩之间的建筑空隙得不到及时充填或压密而为管片上浮提供了空间，但部分工程实际却显示管片上浮量随注浆量增加而增加，反之减小并出现下沉[9]；张海涛[10]认为同步注浆浆液配比不合理，导致盾构管片长时间包裹于悬浮的流塑状浆液中而上浮；Maidl[11]、戴小平[12]和沈林冲[13]认为盾构隧道上覆土体过薄或连接螺栓抗剪能力不足致使管片上浮，但在隧道覆土较大和硬质岩体地层中也出现了管片上浮现象[1]；肖明清[14]和魏纲[15]认为同步注浆过程中注浆压力会对管片位移产生影响，但具有偶然性， “下大上小”的地应力分布是管片上浮的根本原因；唐孟雄[16]和叶飞[17-19]将管片上浮归纳为下述5个方面：(1)浆液包裹而产生的静态上浮力；(2)盾尾同步或壁后注浆充填、渗透及压密而产生的动态上浮力；(3)上覆土的反向压缩作用；(4)由于千斤顶顶力不均匀而引起的纵向偏心荷载；(5)隧道上方的基坑开挖等工况对隧道结构产生卸载效应。因此，关于上浮的因素和作用机理，有必要进一步厘清各因素对上浮影响的贡献率，抓住主要影响因素进行深入分析，为上浮计算模型提供理论基础。

2.2　横、纵向刚度研究方法

在盾构横向刚度研究中，国内外众多学者从方便工程运用角度将其转化为横向弯曲刚度有效率η和弯矩提高率ξ来考虑[20-22]，但η和ξ如何取值，学术界还存在较大分歧。其主要有以下3种方法。一是，以经验或试验取值。日本土木学会[23]对混凝土平板管片进行原型加载试验，指出η取0.7、ξ取0.4的建议；Kashima[24]通过圆角矩形管片加载试验，获得了η取0.75的结论；Muir Wood[25]基于等分块的衬砌环模型试验，指出接头数超过4的管片才考虑接头对管片环整体刚度影响；黄宏伟等[26]以上海错缝管片为原型进行了相似模型试验，给出错缝管片η的合理取值为0.8；封坤等[27]对高压水隧道(南京长江隧道和广州狮子洋隧道)展开了原型试验，指出10 m和15 m级水下盾构隧道通、错缝条件下η、ξ的建议值。上述试验方法及结论真实可信，但只是针对单一实例工程，不具普遍性。二是，以“梁-弹簧”模型为基础，获得修正惯用法所需要的η再通过惯用法求解。Lee等[28]以盾构等效直径为依据，对影响弯曲刚度的相关因素(接头刚度、管片直径、地层抗力)分析，并指出软土盾构隧道刚度有效率可取 0.35；钟小春[29]基于接头刚度模型，提出了简化的“梁-弹簧”模型，并进一步对关键参数进行了探讨。这种方法弹簧参数不易确定，且失去了等效刚度法简捷的优势。三是，理论推导取值。刘建航和候学渊[30]假定管片环向接头等距离分布，推导了轴对称条件下横向弯曲刚度有效率η的理论公式；张建刚和何川[31]提出用“代表区段”体现整环结构弯曲刚度的思想，建立了通、错缝管片弯曲刚度有效率和弯矩提高率的理论公式，并与文献[30]对比，验证理论公式合理性。但“刘-候”公式适用面很窄，“张-何”公式没有考虑管片横向分段不均的实际情况。

在盾构纵向刚度研究中，大多数纵向分析都忽略横向变形的影响。以日本志波由纪夫[32-33]为代表的纵向等效连续梁模型应用最为广泛。该模型假定横向为均质圆环，视纵向为管片和接头组成具有相同弯曲刚度的均匀梁体；田敬学和徐凌等[34-35]在志波由纪夫基础深化了等效连续梁模型，获得了考虑轴向刚度和纵向等效抗弯刚度的计算方法；朱合华和廖少明等[36-37]在其提出了纵向“梁-弹簧”模型，并对管片环间接头的作用范围和效果进行了深入探讨，并进一步获得了纵向等效刚度的计算公式。上述文献均未考虑横向刚度对盾构隧道纵向刚度的影响。张文杰等[38]在传统纵向等效连续化模型基础上，考虑横向刚度的影响和纵向环缝影响，提出了广义的盾构纵向等效连续化模型；叶飞等[39]在横向修正惯用法基础上，将η引入到纵向等效连续梁模型中，推求了考虑横向刚度有效率的纵向等效抗弯刚度计算公式。但张氏模型，忽略了螺栓预紧力影响，叶氏模型忽略了螺栓预紧力和环缝作用范围的影响。如何综合考虑上述因素，建立更为完善的等效刚度理论还有研究的空间。同时，在研究方法上，能否摒弃传统的两种研究方法(横、纵向刚度等效率和梁-弹簧模型)，提出新的折中的简化模型。通过简化模型的建立，避免梁-弹簧模型参数不易确定以及等效刚度法忽略“圣维南”局部变形原理而进行一味均一化的不合理性。

2.3　横、纵向浆液分布模型

根据盾构壁后注浆浆液的扩散过程，可将注浆分为充填注浆、渗透注浆、压密注浆和劈裂注浆4种[19]。叶飞等[40-41]基于球面扩张理论和柱面扩张理论深入研究了盾构壁后注浆浆液扩散对管片产生的压力荷载传递规律，并获得了管片压力理论计算公式；文献[42]在叶飞研究的基础上，基于球形扩张理论考虑浆液黏度时变性进一步推求了浆液扩散过程与管片所受压力间的关系；李志明、白云、袁小会和范昭平等[43-46]假定盾尾四周土体为黏性土(浆液不渗透)，浆液分别为牛顿流体和宾汉流体，从流体力学角度获得了同步注浆浆液充填力学模型；叶飞等[47]假定浆液呈半球形扩张，应用弹塑性理论建立了壁后注浆压密模型并进行了参数敏感性分析。上述文献表明：一方面，国内外学者多割裂注浆各个阶段的联系而单一分析浆液充填注浆阶段(浆液自由填充)和渗透扩散阶段(半球面扩散和弧面扩散)，且仅有文献[47]研究了压密注浆过程。盾尾注浆后，依次经历充填、渗透、压密和劈裂阶段，如何建立合适模型同时考虑浆液动态变化过程力学模型还有待进一步研究；另一方面，上述所有文献在探讨浆液分布时都做了“周围土体为黏性土”的假定，即忽略盾尾浆液不向周围黏土层发生渗流，这与实际土质多样性存在较大出入。

有关纵向浆液分布模型研究的文献并不多见，仅李志明[43]将盾构充填注浆分为横、纵向两个独立过程。横向填充模型同文献[43-46]，纵向填充模型利用梁精华[48]壁后注浆单元模型试验的应力应变关系获得，其模型建立的试验基础未详细展开地层条件、初始应力、水压力以及周围土体应力的影响，可信度值得商榷。

2.4　横、纵向上浮计算模型

横向上浮计算模型方面：叶飞[49-50]提出了考虑上浮力引起的局部抗浮计算模型，并进一步分析了管片环间接头效应对抗浮计算的影响；魏纲[15]考虑静、动态上浮力等因素，采用修正惯用法对上浮阶段管片内力进行计算，指出上浮阶段管片内力较正常阶段增加50%左右；戴志仁[51]从设计者角度，对修正惯用法荷载取值进行探讨，提出了基于拱底地层位移趋势的修正惯用计算模型，克服了隧道拱底处安全系数不足的问题；笔者[52]从准静力平衡入手，建立了考虑上浮力及土压力等因素的局部上浮计算模型，并求得了上浮量随时间变化的理论解。叶氏模型虽考虑了上覆土体反向压缩特性，但并未解决管片受力及上浮量问题，仅确定了上覆土体合理厚度；魏氏和戴氏模型均以修正惯用法为基础，对管片上浮阶段进行受力分析过程中并未考虑上覆土体反向压缩特性，且不能获得管片上浮量的预测值。笔者建立的局部上浮模型虽获得了上浮量的理论解，仍然未考虑土体反向压缩。

纵向上浮计算模型方面：余占奎[53]创建了双面弹性地基梁理论，分别获得了集中力、集中力偶、局部荷载和不同地基抗力作用下双面弹性量内力和变形理论解析，但其双面弹性地基理论正确性有待进一步论证；叶飞等[17]依靠数值计算方法，通过在盾构隧道上部与上覆土体间设置弹簧来模拟上覆土体的压缩特性，分析了壁后注浆情况下管片上浮特性，但该模型假定浆液流型和上覆土体基床系数不变与实际情况不符；朱令等[54]基于弹性地基梁理论建立了纵向上浮计算模型，获得了最大上浮量随地层系数、环向螺栓、管片环宽等变化规律，但求解过程仍建立在数值建模计算之上；笔者[55-56]建立了纵向上浮近似计算模型，探求了相应的近似理论解析。上述模型建立均以纵向等效刚度和弹性地基梁为基础，是否有新的上浮计算模型尚有探讨空间。

3进一步研究方向和方法

3.1　管片横、纵刚度计算方法

笔者认为，盾构管片横、纵向刚度可从两个方向或角度开展研究工作。一是，仍从弯曲刚度有效率η和弯矩提高率ξ入手(传统纵向等效连续化模型)，通过几何关系、力学平衡等条件，推求考虑横向弯曲刚度有效率、螺栓预紧力和环缝作用范围的纵向等效刚度，为后续纵向上浮模型提供必要刚度参数；二是，摒弃传统研究的两种方法(横、纵向等效率(图1(a)、(b))和梁-弹簧模型(图2(a)、(b)))，提出横、纵向折中“梁-梁”简化模型，暂定为“局部刚度修正梁-梁”模型(图1(c)和图2(c))，即通过模型试验或与梁-弹簧模型对比，确定局部管片横、纵接头修正系数，非接头管片段不做刚度修正或转化为变截面梁求解(接头部位刚度折减转化为截面几何参数减小)。

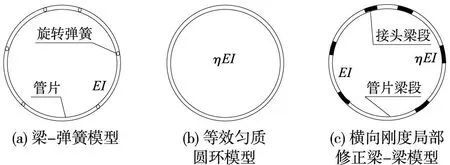
图1　横向刚度求解模型

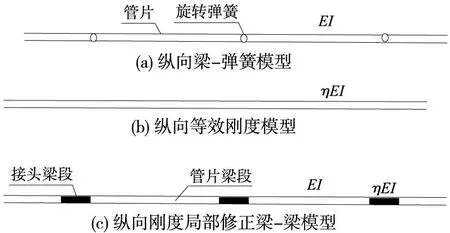
图2　纵向刚度求解模型

现设计横断面模型试验，确定“局部刚度修正梁-梁”模型的修正系数为例来说明。弯曲刚度是结构自身固有性质，与外界荷载无关。同时，管片纵向接头影响范围是有限的(圣维楠原理)，接头影响范围外管片变形只与其受到的合力相关，这与管片组成的实际情况相一致。以横断面为例，设计“2片相邻管片块+1个接头”相似模型试验，拟采用乙稀管(PE 管)模拟管片，环向接头由螺丝+薄塑料片(PE 片)模拟。一边活动铰支座，一边为链杆支撑，采用集中上部集中对称加载方式，加载模型如图3(a)所示(P为竖向荷载，N为轴向荷载)，等效局部刚度修正梁-梁模型见图3(b)。根据变刚度梁理论和图乘法，推求扰度相等条件下等效模型中η和l(η为接头刚度有效率，l为接头等效长度)。

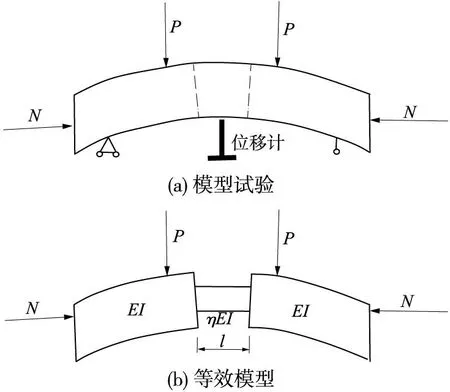
图3　刚度修正模型试验

3.2　横、纵向上浮力分布规律和计算公式

2.3节众多文献多将同步注浆过程和横纵向浆液填充视为两个独立过程，与实际不符。本文提出将同步注浆过程视为充填和渗透两个连续阶段。首先利用流体力学理论对充填过程进行了理论分析。考虑到盾构推进速度较慢及浆液沿环向充填到最远距离所需时间很短，可视为同步注浆过程浆液仅沿环向充填盾尾间隙，分别假定浆液为宾汉姆流体和牛顿流体，推求浆液充填过程浆液压力沿盾尾间隙环向分布模型；然后以充填浆液分布模型为基础，考虑浆液固结收缩，基于达西定律、广义胡克定律以及微元平衡，探求浆液环饼和压力消散与时间的公式及变化规律；最后根据横断面上浮力分布规律，结合盾构推进速度，给出浆液时变性下纵向上浮力分布规律，为后续上浮计算模型提供荷载施加依据。

3.3　管片横、纵向上浮计算模型及解答

梁-弹簧模型和壳-弹簧模型，由于弹簧参数选取随机性较大且不易获取，实际工程中多采用弹性地基圆梁法和修正惯用法。弹性地基圆梁法(图4(a)、(b))常常计算出拱底为向下位移，与实际情况不符；修正惯用法又无法考虑管片上浮过程中上覆土体反向压缩特性。本文研究思路为：将全周弹簧模型(图4(a))和局部弹簧模型(图4(b))改良为可考虑反向压缩且不会出现拱底向下位移的局部弹簧模型(图4(c)、4(d))，图4(c)以等效刚度理论为依据，将管片环视为刚度等效匀质圆环，图4(d)以局部刚度修正理论为依据，将不均质圆环视为作用于可考虑反向压缩特性的弹性地基中进行求解，至此，施加主动荷载即可求管片上浮量数值解，并定义图4(c)、4(d)为抗力反转局部上浮计算模型。为进一步寻求理论解，将图4(c)反向压缩弹簧等效为单根弹簧，进而转化为单一质点(管片)在地应力q1、q2和e、静动态上浮力Ff、浆液对管片的黏滞阻力Ft、上覆土反向压缩Fk等因素共同作用下的准静力平衡问题(图4(e))。

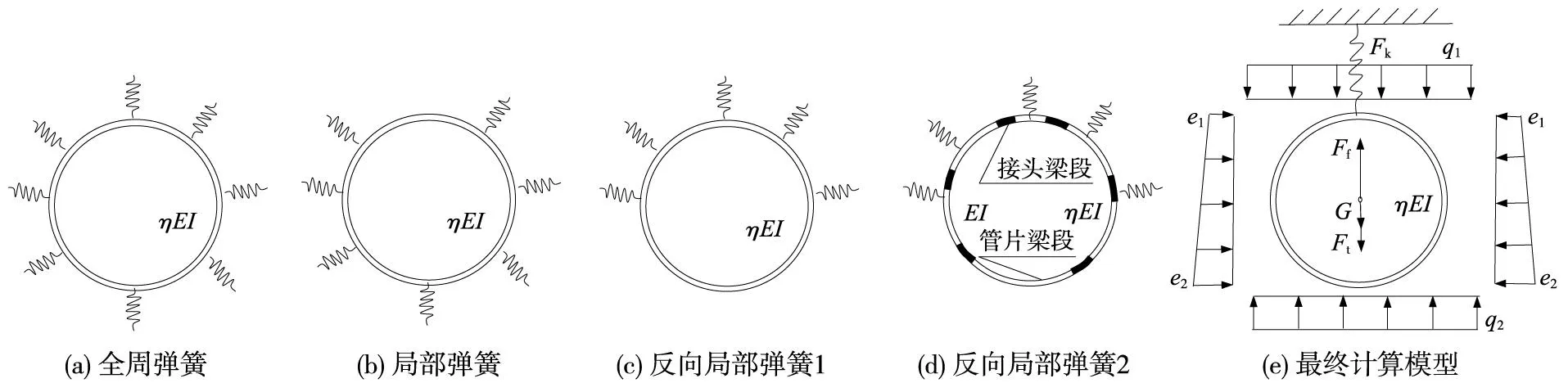
图4　横向上浮计算模型演变

纵向上浮计算模型建立主要考虑2种。一是以纵向等效刚度为基础(图5(a))，考虑上浮荷载(Ff(x))和不同基床系数(k1、k2和k3)，基于有限元理论、弹性地基梁的弯曲微分原理以及梁段间协调条件推求盾构隧道纵向上浮理论解；二是以纵向刚度局部修正梁-梁模型为基础(图5(b)，参数含义同图5(a))，考虑管片上浮等影响因素，基于变截面弹性地基梁理论，运用力学和数学知识，求解管片上浮的计算表达式。在上述两种纵向上浮计算模型的基础上，更改winker弹性地基梁为Pasternak或Kerr地基，可进一步寻求相应模型纵向上浮数值解或解析解。

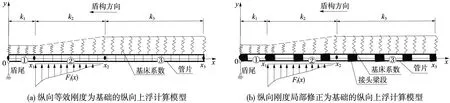
图5　纵向上浮计算模型

4结语

随着我国各大城市地铁和江河海底盾构隧道的兴建，施工过程中管片上浮问题愈发凸显。盾构设计者不仅要从管片受力角度考虑设计，更应从上浮量预测角度把控盾构管片设计，而不是仅仅将上浮位移控制放置于施工过程中，避免由于上浮问题造成隧道侵限，更甚者需要调整线路来解决上浮造成的管片漂移。通过对国内外已有研究现状分析，指出现有上浮研究存在的问题，并进一步提出了相应研究方向和方法，希望对作类似研究的学者提供一定参考和借鉴。

(1)盾构隧道上浮计算模型研究过程必须首先解决管片四周浆液分布和压力大小问题，已有研究多割裂浆液充填、渗透、压密和劈裂的连续过程，如何建立与实际更为贴切的计算模型仍是今后研究的难点。

(2)已有研究成果多延续等效刚度思想，通过模型试验和数值计算等手段集中于刚度有效率η和弯矩提高率ξ研究，从而便于横断面设计。进一步厘清横、纵向刚度内在联系，建立有效的盾构隧道纵向计算模型成为隧道界急需解决的问题。

参考文献：

[1]丁德云，鲁卫东，杨秀仁，等.大直径盾构隧道扩挖地铁车站的力学性能研究[J].岩土力学，2010，31(S2)：281-287.

[2]刘千伟.上海长江隧道建设关键技术综述[C]∥地下工程建设与环境和谐发展—第四届中国国际隧道工程研讨会文集.上海:同济大学出版社，2009:54-65.

[3]姚超凡，晏启祥，何川，等.盾构隧道内力分析方法的对比研究[J].铁道标准设计，2013(12):95-99.

[4]姚超凡，晏启祥，何川，等.深埋双圆盾构隧道的横向地震响应特性研究[J].铁道标准设计，2014，58(4):74-77.

[5]叶慷慨.盾构隧道管片位移分析[J].隧道建设，2003，23(5)：8-10.

[6]黄威然，竺维彬.施工阶段盾构隧道漂移控制的研究[J].现代隧道技术，2005，42(1)：71-76.

[7]Lo K Y， Ng M C, Rowe R K. Predieting settlement due to tunneling in clays[A]. Tunnelling in soil and Rock， ASCE Geoteeh 111 conferenee[C]. Atlanta，GA， 1984:46-76.

[8]姜忻良， 崔奕， 李园，等.天津地铁盾构施工地层变形实测及动态模拟[J].岩土力学，2005，26(10):1612-1617.

[9]周文波，吴惠明.观光隧道盾构叠交施工技术初探[J].中国市政工程，2002，100(4):20-23.

[10]张海涛.盾构同步注浆材料试验及隧道上浮控制技术[D]. 上海:同济大学，2007.

[11]Maidl B， Herrenknetcht M， Anheuser L. Mechanised Shield Tunnelling[M]. Berlin: Ernst & Sohn Verlag für Architektur und techn.Wissenschaften Gmb H， 1996.

[12]戴小平，郭涛，秦建设.盾构机穿越江河浅覆土层最小埋深的研究[J].岩土力学，2006，27(5):782-786.

[13]沈林冲，钟小春，秦建设，等.钱塘江盾构越江隧道最小覆土厚度的确定[J].岩土力学，2011，32(1):111-115.

[14]肖明清，孙文昊，韩向阳.盾构隧道管片上浮问题研究[J].岩土力学，2009，30(4):1041-1056.

[15]魏纲，洪杰，魏新江.盾构隧道施工阶段管片上浮的力学分析[J].岩石力学与工程学报，2012，31(6):1258-1263.

[16]唐孟雄，陈如桂，陈伟.广州地铁盾构隧道施工中管片受力监测与分析[J].土木工程学报，2009，42(3)：118-124.

[17]叶飞，朱合华，丁文其.基于弹性地基梁的盾构隧道纵向上浮分析[J].中国铁道科学，2008，29(4)：65-69.

[18]叶飞，何川，王士民.盾构隧道施工期衬砌管片受力特性及其影响分析[J].岩土力学，2011，32(6)：1801-1807.

[19]叶飞.软土盾构隧道施工期上浮机制分析及控制研究[D]. 上海：同济大学，2007.

[20]日本铁道综合技术研究所.铁道构造物等设计标准·同解1758岩土工程学报2011年说—シ一ルドトンネル[M].日本:丸善发行所，1997.

[21]铃木章. シ-ルドトンネルの新技术[M].東京:土木工学社，1995.

[22]MURAKAMI H， KOIZUMI A. Study on load bearing capacity and mechanics of shield segment ring[J]. Proc. for the Japan Society for Civil Engineers， 1978，272(4):103-115.

[23]土木学会.隧道标准规范(盾构篇)及解说[M].朱伟， 译. 北京:中国建筑工业出版社，2001:68-73.

[24]Kashima Y， Kondo N， Inoue M. Development and application of the DPLEX shield method: Results of experiments using shield and segment models and application of the method in tunnel construction[J].Tunnelling and Underground Space Technology， 1996，11(1):45-50.

[25]Muir Wood A M. The circular tunnel in elastic ground [J].Geotechnique， 1975，25(1):115-127.

[26]黄宏伟，徐凌，严佳梁，等.盾构隧道横向刚度有效率的研究[J].岩土工程学报，2006，28(1):11-18.

[27]封坤，何川，夏松林.大断面盾构隧道结构横向刚度有效率的原型实验研究[J].岩土工程学报，2011，33(11):1750-1758.

[28]Lee K M， Hou X Y， Ge X W， Tang Y. An analytical solution for a jointed shield-driven tunnel lining[J]. International Journal for Numerical and Analytical Methods in Geomechanics， 2001，25(4):365-390.

[29]钟小春，张金荣，秦建设，等.盾构隧道纵向等效弯曲刚度的简化计算模型及影响因素分析[J].岩土力学，2011，32(1)：132-136.

[30]刘建航，侯学渊.盾构法隧道[M].北京:中国铁道出版社，1991:232-238.

[31]张建刚，何川.盾构隧道衬砌整环力学机理模型[J].工程力学，2013，30(7):137-146.

[32]志波由纪夫，川岛一彦，大日方尚己，等.应答变位法に ょるツールドトネルの耐震设计法[J].土木技术资料，1986，28(5)：45-52.

[34]田敬学，张庆贺.盾构法隧道的纵向刚度计算方法[J].中国市政工程，2001(3):35-37.

[35]徐凌.软土盾构隧道纵向沉降研究[D].上海：同济大学，2005.

[36]朱合华，崔茂玉，杨金松.盾构衬砌管片的设计模型与荷载分布的研究[J].岩土工程学报， 2000，22(2):190-194.

[37]廖少明.圆形隧道纵向剪切传递效应研究[D].上海：同济大学，2002.

[38]张文杰， 徐旭，李向红，等. 广义的盾构隧道纵向等效连续化模型研究[J].岩石力学与工程学报，2009，28(S2):3938-3944.

[39]叶飞，何川，朱合华，等.考虑横向性能的盾构隧道纵向等效刚度分析[J].岩土工程学报，2011，33(12):1870-1876.

[40]叶飞，苟长飞，刘燕鹏，等.盾构隧道壁后注浆浆液时变半球面扩散模型[J].同济大学学报：自然科学版，2012，40(12):1789-1794.

[41]叶飞，苟长飞，陈治，等.盾构隧道黏度时变性浆液壁后注浆渗透扩散模型[J].中国公路学报，2013，260(1):127-134.

[42]Yuan J X， Wang D Y, Wang D. Study on model of back-filled grouting of shield tunnel[J]. Advanced Materials Research， 2014(919-921)：883-886.

[43]李志明，廖少明，戴志仁.盾构同步注浆填充机理及压力分布研究[J].岩土工程学报，2010，32(11):1752-1757.

[44]白云，戴志仁，张莎莎，等.盾构隧道同步注浆浆液压力扩散模式研究[J].中国铁道科学，2011，32(4):38-45.

[45]袁小会，韩月旺，钟小春.盾构隧道壁后注浆压力分布模型[J].西南交通大学学报，2011，46(1):18-25.

[46]范昭平，韩月旺，方忠强.盾构壁后注浆压力分布计算模型[J].公路交通科技，2011，28(3)：95-100.

[47]叶飞，陈治，苟长飞，等.基于球孔扩张的盾构隧道壁后注浆压密模型[J].交通运输工程学报，2014，14(1)：36-42.

[48]梁精华.盾构隧道壁后注浆材料配比优化及浆体变形特性研究[D].南京:河海大学，2006.

[49]叶飞，朱合华，丁文其，等.大断面盾构隧道施工抗浮计算研究[J].地下空间与工程学报，2007，3(5):849-8531.

[50]叶飞，朱合华，丁文其.盾构隧道抗浮计算模式及其适应性分析[J].公路交通科技，2009，26(5):91-96.

[51]戴志仁.盾构隧道衬砌结构计算模型探讨[J].铁道工程学报，2013(6)：52-58.

[52]D.Y.Wang，D.Li and J.X.Yuan.Study on Rising Displacement of Segment of Shield Tunnel in Soft Soils， Applied Mechanics and Materials， 2014(501-504)：1684-1687.

[53]余占奎.软土盾构隧道纵向设计方法研究[D].上海:同济大学，2006.

[54]朱令，丁文其，杨波.壁后注浆引起盾构隧道上浮对结构的影响[J].岩石力学与工程学报，2012，31(S2):3378-3382.

[55]王道远，袁金秀，朱正国，等.水下盾构隧道纵向上浮理论解及工程应用[J]. 岩土力学，2014，35(11)：3079-3085.

[56]王道远，王锡朝，袁金秀，等.运河开挖卸载下水下盾构隧道纵向上浮量预测研究[J].现代隧道技术，2015，35(2)：3079-3085.

Review on Prediction of Upward Movement of Shield Tunnel in Soft Soil during Construction

WANG Dao-yuan1，2，3, ZHU Yong-quan1，3, HE Chuan1

(1.School of Civil Engineering， Southwest Jiaotong University， Chengdu 610031， China; 2.Department of

Civil Engineering， Hebei Jiaotong Vocational and Technical College， Shijiazhuang 050091， China;

3.School of Civil Engineering， Shijiazhuang Tiedao University， Shijiazhuang 050043， China)

Abstract：With the development of shield tunnels for urban subway or passages underwater， the upward moving of tunnel segment has become a challenge during the construction. Firstly， the current researches and problems are reviewed in terms of floating mechanism， relationship between lateral and vertical rigidity， distribution law of the buoyancy and floating calculation model. Secondly， based on the existing research results， new ideas and research directions are proposed， including (1) probing distribution rule and calculation figure when backfill grouting filling and penetration are taken as a continuous process; (2) putting forward local modified lateral and vertical stiffness(BBM) model in stead of the traditional rigidity model and beam-spring model; (3) defining the inapplicability of the round elastic foundation beam method and modified routine method in the analysis of upward movement during construction and addressing the applicability of the resistance inversion model; (4) considering the factors of time-varying grouting， earth stress， buoyancy and compression of the overburden soil， and setting up the model of static buoyancy and dynamic buoyancy based on the equivalent rigidity and BBM. Finally， some practical suggestions are offered.

Key words：Shield tunnel; Construction period; Upward movement of segment; Prediction

作者简介：王道远(1982—)，男，讲师，博士研究生，2005年毕业于石家庄铁道大学土木工程学院桥梁与隧道工程专业，主要从事隧道及地下工程教学和研究工作，E-mail：wtg-888@163.com。

基金项目：国家自然科学基金资助(51478277)；河北省自然科学基金资助(E201619002)；河北省人才工程培养经费资助科研项目(A20150 0116)；河北省高等学校科学技术研究青年基金(QN2014161)。

收稿日期：2015-05-15； 修回日期：2015-06-07

中图分类号：U455.43

文献标识码：ADOI:10.13238/j.issn.1004-2954.2016.01.020

文章编号：1004-2954(2016)01-0092-06