基于BP神经网络的黄土湿陷起始压力的预测

陈佳玫，张爱军，邢义川，张婉

（1.西北农林科技大学水利与建筑工程学院，陕西杨凌712100；2.中国水利水电科学研究院，北京100048）

基于BP神经网络的黄土湿陷起始压力的预测

陈佳玫1，张爱军1，邢义川2，张婉1

（1.西北农林科技大学水利与建筑工程学院，陕西杨凌712100；2.中国水利水电科学研究院，北京100048）

黄土的湿陷起始压力是评价黄土湿陷性的重要指标之一。影响黄土湿陷起始压力的因素有很多，且各因素间并非独立，通过分析各物性指标间的相关性确定塑性指数、含水率、干密度作为影响黄土湿陷起始压力的因素。本文提出并建立了黄土湿陷起始压力的人工神经网络预测模型，选取新疆伊犁地区黄土的数据作为神经网络模型的学习和预测样本，将神经网络模型的预测结果与实际结果对比可知二者误差小于10%。利用陕西彬县黄土数据验证了网络模型的通用性，说明用人工神经网络方法计算黄土湿陷起始压力准确、可靠，建立了一种计算湿陷起始压力的新方法。

湿陷起始压力；物性指标；人工神经网络；预测

1 研究背景

我国的黄土分布面积居世界首位。黄土的湿陷性是黄土最重要的工程特性之一，许多建构筑物都因为黄土湿陷而破坏，产生了重大影响。在工程实践中，为了评价分析黄土的湿陷性，需进行大量湿陷试验，试验工作量通常很大，费时费力，且测试结果随着试样的不均匀性，以及试验条件和测试技术不同，变化幅度较大，精度有限［1］。因此需要人们对已有资料统计分析，并建立相应的模型，以期能够对未来样本准确地预测。研究显示，黄土湿陷由多因素共同影响。不同地区黄土的湿陷性有所差别，对于同一地区的黄土来说，显著影响湿陷性的是其物性指标［2］，且物性指标容易测得，误差小、较稳定，目前已有很多学者研究了黄土湿陷特性参数与基本物性指标之间的关系。

湿陷起始压力是黄土湿陷的重要指标，其实质是上覆压力界限值，若上覆压力不大于该值，即使黄土遇水浸湿也不会湿陷。分析场地的湿陷性、计算湿陷量、选择场地处理措施都必须结合湿陷起始压力。研究表明，湿陷起始压力与黄土的基本物理力学指标的关系比较复杂，并不是简单的线性关系，很难用数学、力学方法准确地总结［3-4］。人工神经网络模型具有较强的学习、识别能力，可以仅在了解输入信息和输出信息的前提下就建立起复杂的非线性映射关系［5］，而无需了解其中具体的数学关系。因此，本文运用人工神经网络方法，对湿陷起始压力进行预测，并与实际数据对比验证，以期在取得黄土的基本物理力学指标和少量湿陷起始压力的试验数据后，即可预测其湿陷起始压力值。

2 黄土湿陷起始压力的影响因素分析

湿陷起始压力是评价黄土湿陷的一项重要指标，一般采用单线或双线法进行室内浸水压缩试验，做出δs-P曲线并求出湿陷系数等于0.015时的压力值，即为湿陷起始压力。影响湿陷起始压力的因素有很多，其中宏观物理因素有液限、塑限、塑性指数、含水率、饱和度、干密度和孔隙比，它们之间并不完全独立，其间具有一定的相关性。本文采用的数据（见表1）来源于文献［6］，土样取自新疆伊犁的阿克达拉水电站工程。水电站工程的引水渠道有12 km渠段建设在强烈湿陷性黄土地区，湿陷性黄土厚度大于30 m，属自重中、强湿陷性黄土。取样位置位于现场试验段的轴线上，表1中编号1—2的土样取自探坑TK2-1，位于试验段平台顶面以上，用于代表试验段已经开挖掉部分原生黄土的特性；编号3—31的土样取自探坑TK2，位于试验段中心，用于代表整个试验段相应高程的原生黄土的特性；编号32—35的土样取自探坑TK3，位于原强夯试验段内，具体位置为该段黄土冲沟底部，鉴于该冲沟内曾经受到长期水流浸湿，该探坑土样用于代表受到过水浸湿影响的次生黄土的性能。本文利用SPSS统计分析软件，根据因子分析的原理，将搜集到的试验数据标准化后，计算各物性指标间相关系数，并得到它们的相关矩阵，见表2。由表2可以看出，塑性指数和液限、塑限的相关性都比较强，说明它们之间是不独立的，用塑性指数就可以代表这3个参数；含水率和饱和度之间、干密度和孔隙比之间的相关性也很强，用含水率和干密度就可以代表这些指标；其余指标之间的相关系数都不大，表现出较弱的相关性。这样就可以选用塑性指数、含水率、干密度3个指标作为影响黄土湿陷起始压力的因素。塑性指数是黏性土液限与塑限的差值，其值越大，表明黏性土可塑性越强。塑性指数综合反映了土颗粒大小及其矿物组成。这里所说的含水率指的是土的初始含水率，即黄土在进行湿陷试验时浸水前的含水率。黄土属于水敏性的土，含水率是影响黄土湿陷的关键因素。干密度是单位体积土粒数量的多少，反映了土的密实程度，制约着黄土的湿陷，是影响黄土湿陷性的重要指标。这些宏观影响因素是湿陷性黄土微观结构本质的反映。

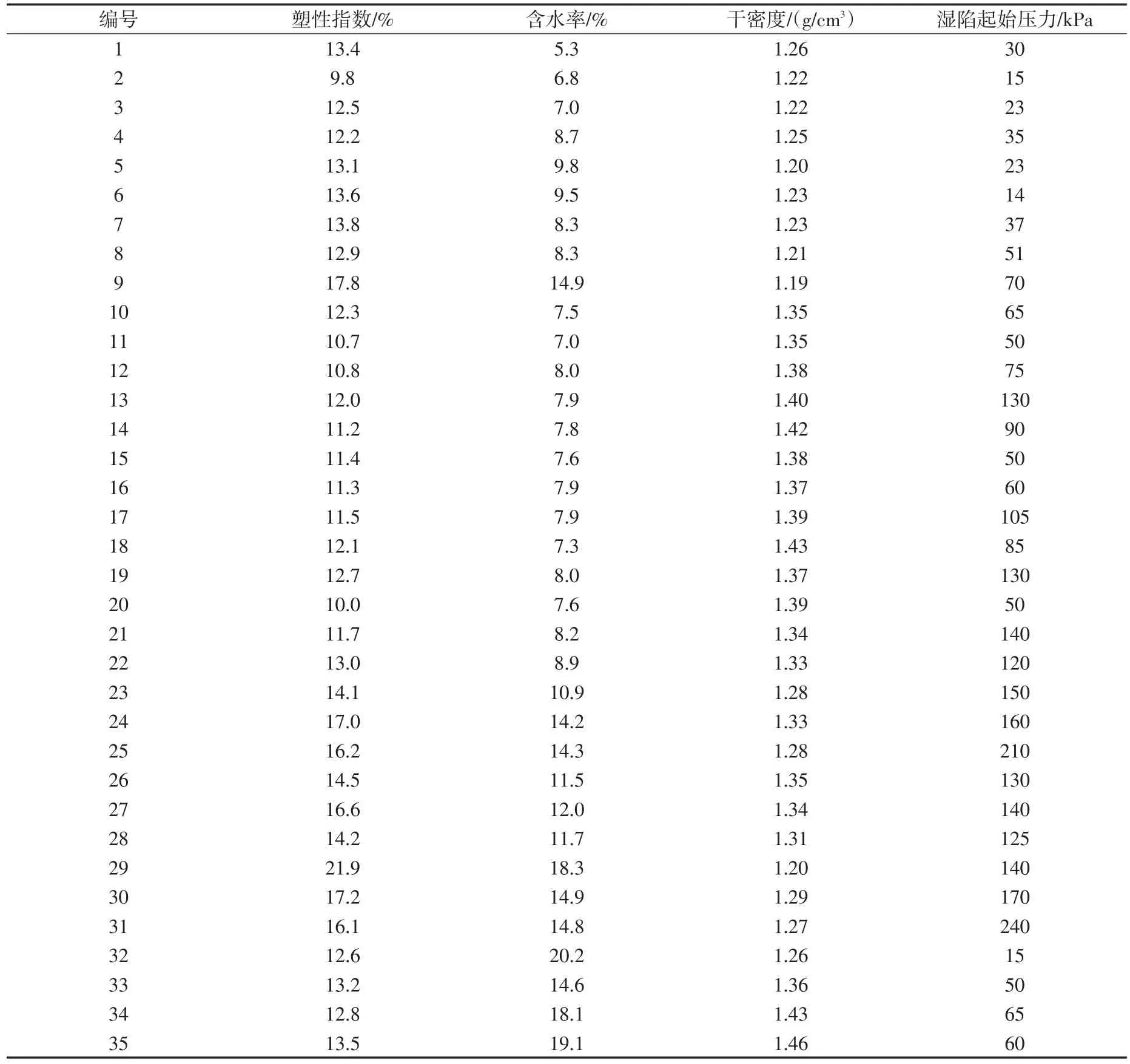
表1 黄土的物性指标与湿陷起始压力

表2 各物性指标之间的相关系数

3 黄土湿陷起始压力的BP神经网络预测

3.1 BP神经网络的基本原理人工神经网络（Artificial Neural Network），一直是人工智能领域研究的热点问题。人工神经网络的本质就是利用某种函数，对认知空间进行划分和分类，可以高度实现神经网络输入因素与网络输出目标之间的非线性映射关系［7］。经过多年的研究和发展，目前已经有很多种人工神经网络模型被研究和使用［8］，而BP神经网络［9］是这些模型中应用最广泛、最成熟的网络模型之一。BP（Back Propagation）神经网络是典型的前馈神经网络模型，通过误差逆向传播算法对网络进行训练。BP神经网络能够学习和存储大量的学习数据中输入信息和输出结果之间的映射关系，并且不需要去理解这种映射关系下存在的数学模型以及具体的公式和结构。BP神经网络模型是一种由输入层（input）、隐含层（hidden layer）和输出层（output layer）三层组成的网络拓扑结构。输入层负责接收来自外界的输入信息，并进行简单的处理后将信息传递给隐藏层的神经元；隐藏层为单层或多层结构，负责处理输入层传来的信号并处理传送给输出层；最终由神经网络的输出层负责向外界传送输入信息的处理结果。当实际输出结果与期望输出结果不相符时，通过误差逆传播算法，按梯度下降的方式去修正神经网络中各层的权值和阈值，由输出层开始，不断地向隐藏层节点、输入层节点逐层反向传递。经过多次的正向网络训练和反向网络调整之后，直到网络的识别误差达到可接受的范围，或者网络达到规定的训练次数之后，则停止训练，网络构建完成。

算法的执行步骤如下：

（1）对权值系数Wij设初值：对各层权值系数Wij设一个较小的非零随机值，其中Wi，n+1=-θ。

（2）输入样本X=（X1，X2，…，Xn，1），以及对应的期望输出Y=（Y1，Y2，…，Yn）。

（3）计算各层的输出，对于第K层第i个神经元的输出，有：

（4）求各层的学习误差。

（5）修正权值系数Wij和θ：

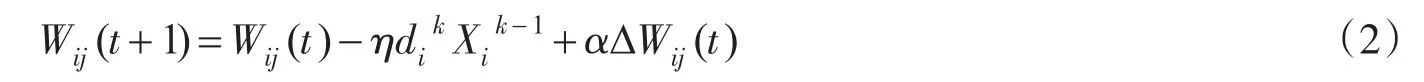
其中：

（6）求出各层的系数后，计算是否满足终止条件，若判定条件满足，则算法结束，否则返回步骤3继续执行，直至满足条件为止。

3.2 BP神经网络模型经上文分析，本文所要建立的神经网络模型中输入节点为3个，输出节点为1个，因此，确定BP神经网络模型结构中的主要任务就是确定网络隐藏层数和每一层的隐藏层节点个数。研究表明，采用单隐藏层的三层神经网络结构能够逼近任意连续函数［10］。因此，本文确定隐藏层的个数为1层，接下来就是确定隐藏层节点的个数，确定隐藏层节点个数的方法主要采用经验公式法［11-12］，根据Kolmogorov定理，最优的隐藏层节点个数计算公式为：

式中M为网络输入层节点个数，H为隐藏层节点个数。根据式（4）进行计算，本文最终确定了网络隐藏层节点数为7个。因此，本文构建了3×7×1的BP神经网络模型。

确定了网络结构之后就是确定各层之间的激活函数，一般选择Sigmoid函数或者双极Sigmoid函数作为网络的激活函数，即：

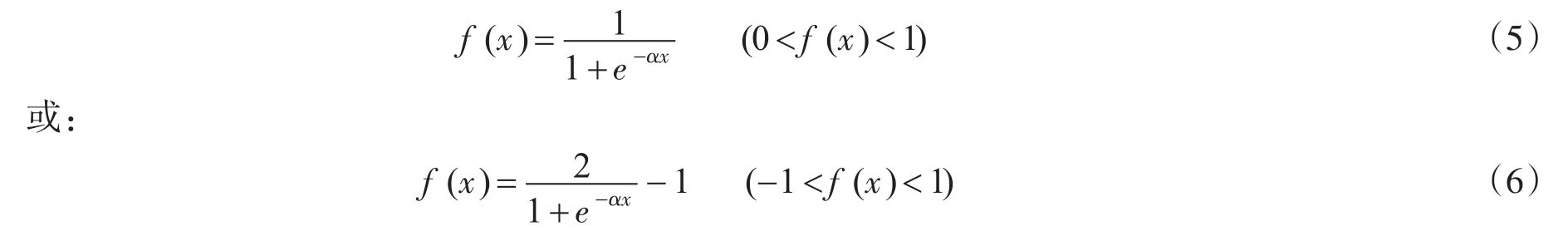
3.3 BP神经网络学习和训练采用表1中的前25组数据作为网络模型学习训练样本，26～35组数据作为预测样本，为了节省篇幅，这里不再列表说明。

首先对学习样本进行训练，为了保证网络能够快速的收敛，减少网络的训练时间，对样本数据进行归一化处理，使得所有的数据都处在［-1，1］范围中，常用的归一化函数为：

由于将训练的样本数据均归一化到［-1，1］范围内，因此输入层到隐藏层的激活函数选择双极Sigmoid函数，隐藏层到输出层的函数选择线性激活函数。

在训练网络的过程中，训练函数选择有动量和自适应lr的梯度下降法，这是目前BP神经网络训练学习中较为常用的一种学习算法，该算法能够快速的收敛并得出结果，设置学习次数为10 000次，目标误差率设置为1%，并对神经网络输出节点的结果四舍五入。

网络经过7 563次训练达到误差要求，训练结束之后，网络的权值和阈值见下表：

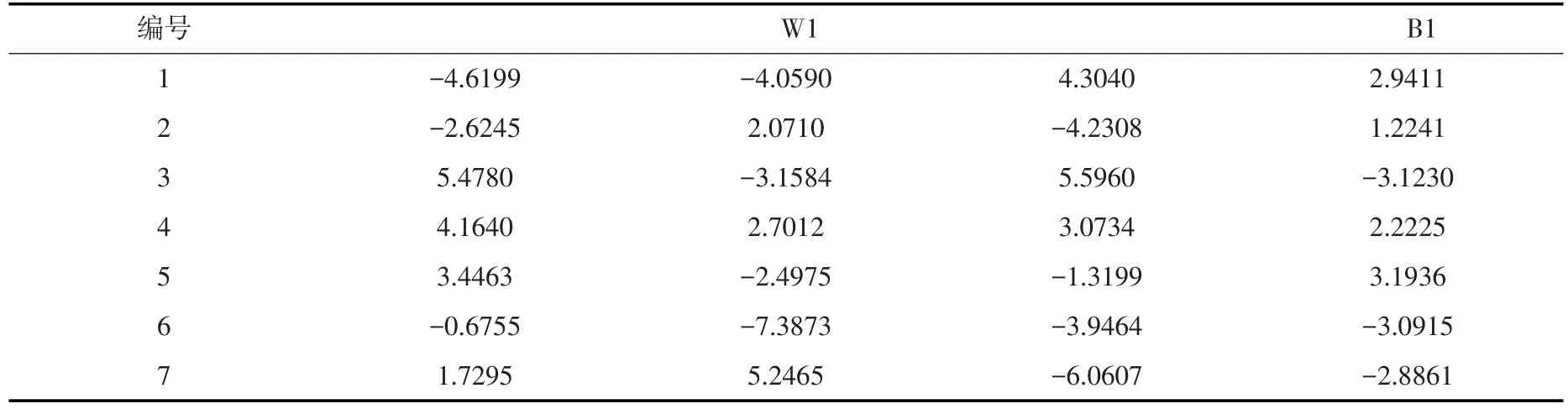
表3 输入层与隐藏层节点权值和阈值

表4 输出层与隐藏层节点权值和阈值

3.4 BP神经网络检测与预测训练后，网络已经达到稳定和最佳训练效果，具有计算黄土湿陷起始压力的能力。为了验证训练效果，对神经网络进行检验，表5为预测结果和误差，湿陷起始压力实际结果与预测结果对比曲线见图1。

由表5可知，利用BP神经网络技术得到的预测结果与实际结果相比最大误差在10%以下，图1显示出二者基本吻合。说明本文选取的影响黄土湿陷起始压力的因素合理，所建立的人工神经网络模型可行，可以采用人工神经网络模型预测湿陷起始压力且预测值具有一定的可靠性。

虽然利用BP神经网络模型预测的湿陷起始压力准确率较高，但预测误差大小不一。根据神经网络模型的特性可知，网络模型的预测需要训练样本和预测样本间具有较高的相似性，若训练数据和预测数据的来源越接近，就可以更多地减少其他因素对样本的影响；若训练数据和预测数据的来源差别较大，则可能存在大量没有作为神经网络输入参数的数据，对网络的认知学习结果产生较大影响，使得网络无法准确的对样本参数特征进行分类，从而导致预测准确率较低，误差较大。与表5中的其他结果相比，7-10的预测误差相对较大，这4组是取自TK3的土样，而训练网络时并没有将TK3的数据作为训练样本，且本文为了使网络模型更加简洁，建立网络模型时也没有将取土地点作为一项输入参数，所以在预测湿陷起始压力时，TK3的预测误差略大。此外，同是TK3的土样，它们的预测误差也存在差异，这可能是取土深度的不同导致的。因此，可能还存在一些黄土的其他影响因素没有在网络模型中考虑到，导致预测结果的误差大小不同。若建立网络模型时，能够加入更多的输入参数，例如取土地点、取土深度、地质年代等影响因素，并且尽量保持预测数据与训练数据的一致性，则预测的误差会更小。但增加网络输入节点个数会导致网络结构更加复杂，训练和预测效率降低，因此，针对不同的土样建立网络模型时，输入节点的选取也应酌情考虑。

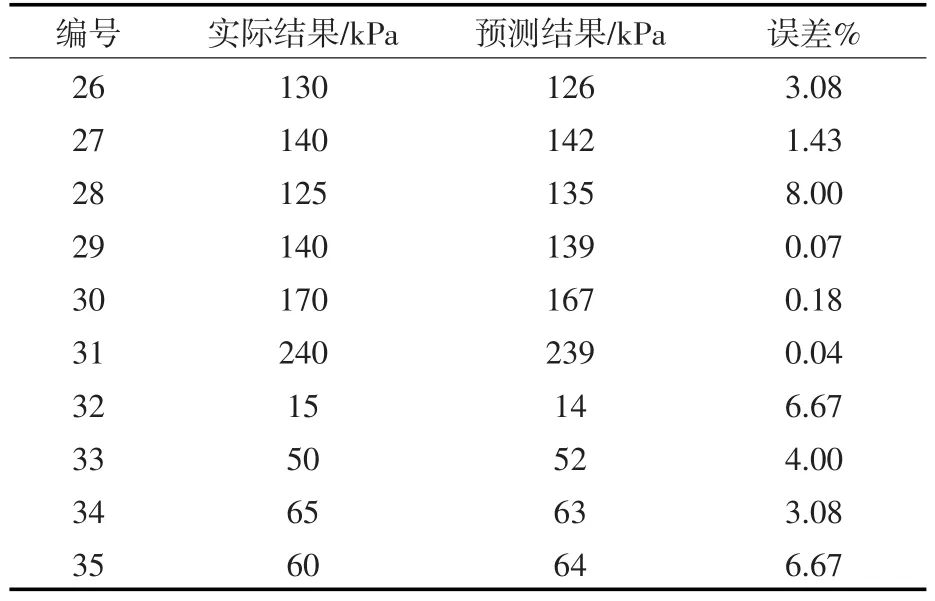
表5 湿陷起始压力预测结果和误差

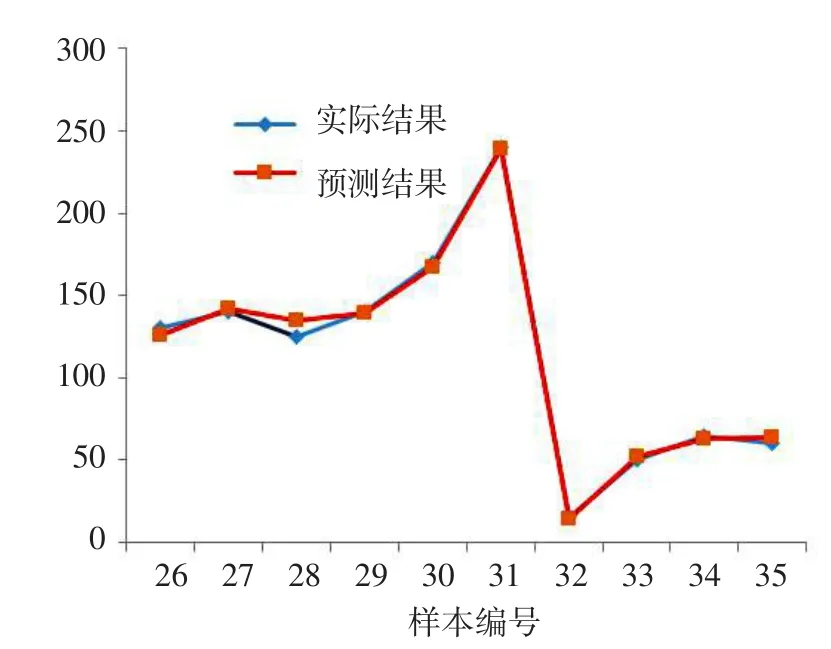
图1 湿陷起始压力实际结果与预测结果对比曲线

3.5 模型通用性检测试验土质、沉积历史和地域对黄土湿陷起始压力的影响很大。采用上文建立的网络模型对文献［4］陕西彬县的37组数据再进行训练和预测，验证该模型的通用性。首先，对数据中的物性指标进行简单换算，得到塑性指数、含水率和干密度3个指标，选取其中27组进行训练，10组进行预测，为了节省篇幅，这里只给出预测样本、结果及误差，见表6。

表6 湿陷起始压力预测结果和误差

由表6结果可知，将本文建立的网络模型运用于陕西彬县黄土湿陷起始压力的预测也得到了较好的结果，误差在10%以下，再次证明了采用人工神经网络模型预测湿陷起始压力的可靠性，同时也证明了该网络模型的通用性。

4 结论

（1）对于同一地质年代、土质和地域的黄土而言，影响黄土湿陷起始压力的主要和独立因素为塑性指数、含水率和干密度，其他因素如孔隙比等可以用以上3个指标代表。

（2）与实测结果对比表明：提出并建立的黄土湿陷起始压力人工神经网络预测模型，对黄土湿陷起始压力的预测具有较高的精确度和方便快速、节省成本的优点，可以用来在进行部分室内试验后预测更多初始情况的黄土的湿陷起始压力，实用性较强。

（3）土质、沉积历史和地域对黄土湿陷起始压力的影响也很大。本文提出的方法只能对同一地区和场地、同一地质年代和土质的土样进行预测，在大量积累不同地质年代、地区和土质的试验资料后，补充地域、地质年代和土质为预测因子后，可以进行大范围的预测工作，这也是笔者今后努力的方向。

［1］刘祖典.影响黄土湿陷系数因素的分析［J］.工程勘察，1994（5）：6－11.

［2］钱鸿缙，王继唐，罗宇生.湿陷性黄土地基［M］.北京：中国建筑工业出版社，1985.

［3］邵生俊，杨春鸣，马秀婷，等.黄土的独立物性指标及其与湿陷性参数的相关性分析［J］.岩土力学，2013（S2）：27-34.

［4］焦振华，李鹏.统计方法在确定黄土湿陷起始压力中的应用［J］.资源环境与工程，2014，28（4）：494-497.

［5］郭文兵，邓喀中，邹友峰.地表下沉系数计算的人工神经网络方法研究［J］.岩土工程学报，2003，25（2）：212-215.

［6］张爱军，郭敏霞，张博.新疆伊犁特克斯河阿克达拉水电站工程引水渠道深厚湿陷性黄土渠基评价与处理专题研究成果报告［R］.2014.

［7］蒋建平，章杨松，阎长虹，等.BP神经网络在地基土压缩指数预测中的应用［J］.中南大学学报：自然科学版，2010，41（2）：722-727.

［8］朱大奇.人工神经网络研究现状及其展望［J］.江南大学学报：自然科学版，2004（1）：103-110.

［9］Mcclelland J L，Rumelhart D E.Explorations in Parallel Distributed Processing：A Handbook of Models，Pro⁃grams，and Exercises［C］//Cambridge University Press，Cambridge Moon Fc.MIT Press，2011.

［10］Curteanu S，Cartwright H.Neural networks applied in chemistry.I.Determination of the optimal topology of mul⁃tilayer perceptron neural networks［J］.Journal of Chemometrics，2011，25（10）：527-549.

［11］Mirchandani G，Cao W.On hidden nodes for neural nets［J］.IEEE Transactions on Circuits&Systems，1989，36：5（5）：661-664.

［12］Lippmann，Richard P.An introduction to computing with neural nets［J］.IEEE Assp Magazine，1987，4（2）：4-22.

Prediction of initial collapse pressure of loess based on the BP neural network

CHEN Jiamei1，ZHANG Aijun1，XING Yichuan2，ZHANG Wan1
（1.College of Water Resources and Architectural Engineering，Northwest Agricultural and Forestry University，Yangling712100，China；
2.China Institute of WaterResources and HydropowerResearch，Beijing100048，China）

The initial collapse pressure of loess is one of the important indicators of evaluation of collaps⁃ibility loess.There are many factors affecting the initial collapse pressure of loess and these factors are not independent.Through the analysis of the correlation between the physical property indexes，this article se⁃lects plasticity index，moisture content and dry density as the influencing factors of initial collapse pressure of loess.This paper puts forward and sets up the artificial neural network prediction model of initial col⁃lapse pressure of loess.Using the data of Xinjiang Ili loess as the training sample and forecast sample of a network model，the paper compared the prediction results of network model with the actual results，and found the error is less than 10%.Network model’versatility was validated by shaanxi Binxian loess data. It illustrates that artificial neural network method to calculate the initial collapse pressure of loess is accu⁃rate and reliable and provides a new method for the calculation of initial collapse pressure.

initial collapse pressure；physical property indexes；artificial neural network；prediction

TU444

A

10.13244/j.cnki.jiwhr.2016.04.003

1672-3031（2016）04-0254-06

（责任编辑：李琳）

2016-03-11

国家自然科学基金（51379220，51279171）

陈佳玫（1991-），女，安徽芜湖人，硕士生，主要从事黄土湿陷性研究。E-mail：chenjiamei1211@163.com

张爱军（1964-），男，山西阳高人，博士，教授，主要从事岩土工程学研究。E-mail：zaj@nwsuaf.edu.cn