同态加密的发展及应用
巩林明 李顺东 郭奕
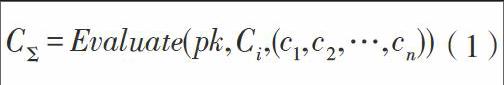
摘要:认为密码学中的同态加密技术可以为分布式计算环境的用户隐私保护提供强有力的技术支撑。同态加密方案被分成3种类型:部分同态加密、浅同态加密和全同态加密。同态加密方案在分布式计算环境下的密文数据计算方面有着重要的应用,包括:安全云计算与委托计算、远程文件存储、密文检索等。指出目前全同态加密方案的构造还处于理论阶段,尚不能用于实际的密态数据计算问题,如何设计基于代数系统的(自然)全同态加密方案依然是未来研究的重点。
关键词:同态加密;密态计算;安全多方计算;安全云计算;分布式计算
Rivest、Adleman和Dertouzos[1]于1978年提出了秘密同态的思想:对几个数据的加密结果进行运算后再解密,得到的结果与这些数据未加密时执行某一运算所得的结果一致。此后,研究人员在同态加密方案设计方面做了大量的工作并取得了大量的研究成果。例如,1978年由Rivest、Adleman和Dertouzos[2]提出的RSA加密系统、1985年由ElGmal提出的ElGmal加密方案[3]、1998年由Okamoto和Uchiyama[4] 提出的《A new public-key cryptosystem as secure as factoring》、1999年由Paillier[5]提出的Paillier加密方案、2002年由Domingo-Ferrer提出的《A provably secure additive and multiplicative privacy homomorphism》、2005年由Boneh [6]等提出的用于保密计算2-析取范式(2DNF)的加密方案、2009年由Gentry等[7]首次提出的全同态加密 (FHE)方案、2010年Dijk[8]等提出的整数域上的FHE方案、2011年由Brakerski、Vaikuntanathan[9]两人提出的基于误差学习的FHE方案、2012年由Brakerski和 Gentry[10]等提出的无需电路自举的分层FHE方案、同年由Brakerski[11]提出的无需模转换的FHE方案、2013年由Gentry[12]等提出的环上的FHE方案、2014年由Brakerski[13]等提出的基于标准误差学习的FHE方案、2015年由Cheon[14]等提出的基于中国剩余定理的整数域上的FHE方案等都是比较著名的同态加密成果。
目前出现的同态加密方案可被分成3种类型:部分同态加密、浅同态加密和全同态加密。部分同态只能实现某一种代数运算(或、乘、加);浅同态能同时实现有限次的加运算和乘运算;全同态能实现任意次的加运算和乘运算。
同态加密方案,除了可以实现加密功能外,还可以用于密文数据的计算。近些年来随着网络技术的发展,以同态加密技术为支撑的密文数据计算越来越多地被应用于各种分布式计算中,例如,安全云计算与安全云存储中有关用户隐私的保护和高效的安全多方计算协议,都需要同态加密技术支持;其他应用如电子选举、远程文件存储、密文检索、版权保护等也都需要同态技术的支持。
1 同态加密系统中的一些定义
(1)同态性
假设一个加密系统的加密函数与解密函数分别为[E:?→C]与[D:C→?],其中[?]与[C]分别为明文空间与密文空间;令[?]和[?]分别为定义在明文空间和密文空间上的代数运算或算术运算。则加密方案的同态性定义为:给定任意的两个[m1,m2∈?],如果一个加密系统的加密函数与解密函数满足代数关系[m1?m2=D(E(m1)?E(m2))](或[E(m1?m2)=E(m1)?E(m2)]),则称该加密系统具有同态性。
(2)加法、乘法、异或同态
一个具有同态性的加密系统,若明文空间上的运算为代数加法“+”,则该加密系统被称为加法同态加密系统;若明文空间上的运算为代数乘法“[?]”,则该加密系统被称为乘法同态加密系统;若明文空间上的运算为算数异或“[⊕]”,则该加密系统被称为异或同态加密系统。
(3)浅同态与全同态
只满足一种代数(或算术)同态运算的加密系统,被称作部分同态加密系统;同时满足加法和乘法同态运算,且只能进行有限次乘法或加法运算的加密系统称为浅同态加密系统;同时满足加法和乘法同态的加密系统称为全同态加密系统。
2 同态加密的发展
同态加密思想从提出到现在,在具体实现方案方面,经历了3个重要时期:1978—1999年是部分同态加密的繁荣发展时期;1996—2009年是部分同态加密与浅同态加密的交织发展时期,也是浅同态加密方案的繁荣发展时期;2009年以后是全同态加密的繁荣发展时期。下面将以时间为主线,按照同态加密方案的类型介绍同态加密的发展。
2.1 部分同态加密方案
部分同态加密方案按照明文空间上能实现的代数或算术运算分为乘法同态、加同态和异或同态3种类型。下面从几个著名的同态加密方案的优缺点入手,总结一下乘法同态、加同态、或同态加密方案的特性。
(1)乘法同态加密方案。乘法同态加密方案的同态性表现为[m1×m2=D(E(m1)×E(m2))]。 RSA [5]是最早的具有乘法同态性的加密方案,它是基于因子分解困难问题的,属于确定性加密,不能抵御选择明文攻击;1985年,ElGamal [3]基于有限域上的离散对数困难假设设计了ElGamal加密算法,该加密方案同样具有乘法同态性,并且满足选择明文不可区分(IND-CPA) 安全。
(2)加法同态加密方案。加法同态加密方案的同态性表现为[m1+m2=D(E(m1)?E(m2))] ([?]为定义在密文空间上的某种代数运算或算术运算)。 具有加法同态性的加密方案有很多,应用最为广泛的当属Paillier [5]加密系统,该加密系统基于高阶合数度剩余类困难问题,且具有IND-CPA安全。
(3)异或同态加密方案。乘法同态加密方案的同态性表现为[m1⊕m2=D(E(m1)?E(m2))]([?]为定义在密文空间上的某种代数运算或算术运算)。目前,只有Goldwasser-Micali [15]加密系统属于该类同态加密系统,该加密系统基于二次剩余困难问题,虽具有IND-CPA安全,但每次只能加密单比特,因此加密效率会比较低。
2.2 浅同态加密方案
浅同态加密方案能同时进行有限次乘法和加法运算的加密。从某种程度上讲,该类型的加密方案是人们在研究解决RSA 3个人提出的公开问题(如何设计全同态加密方案)的过程中,出现的“副产品”。1999—2005年间出现了不少浅同态加密方案,例如文献[6]、[16-18]中提到的方案。目前最为著名的浅同态加密方案当属Boneh[5]等基于理想成员判定困难假设设计的加密方案。该方案能执行一次乘法和若干次加法运算,Boneh [5]等虽然用它成功解决了2DNF问题,但是该方案在解密时需要搜索解密,因此基于此方案的2DNF保密计算协议效率很低。
虽然此类加密系统为实现全同态加密方案的设计奠定了一定的基础,但是只能用于解决某些专门的问题,即能够解决的应用问题有限,很难将其拓展并且应用于解决更广泛的问题。
2.3 全同态加密方案
2009年Gentry[7]设计了首个全同态加密方案,这一里程碑事件激起了全同态研究的热潮。到目前,全同态加密方案按照构造思想大致可以分为以下3代。
(1)以Gentry[7]设计方案为代表的、基于格上困难问题构造的第1代全同态加密方案,这类方案的设计思想大致如下:
·设计一个能够执行低次多项式运算的浅同态加密算法。
·控制密文噪声增长,即依据稀疏子集和问题对解密电路执行“压缩”操作,然后再执行自己的解密函数实现同态解密,从而能够达到降噪的目的。
·依据循环安全假设(即假定用方案的公钥加密自身密钥作为公钥是安全的)实现纯的全同态加密。
(2)以Brakerski-Vaikuntanathan [9]为代表的、基于带误差学习或环上带误差学习困难问题构造的第2代全同态加密方案,该类方案的构造思想大致如下:
·归约的基础是误差学习或环上带误差学习困难问题。
·用向量表示密钥与密文。
·用密钥交换技术来约减密文的膨胀维数,以达到降噪目的。
该类方案的优点是不再需要电路自举技术,突破了Gentry的设计框架,在效率方面实现了很大的提升;其缺点是在使用密钥交换技术时需要增加大量用于密钥交换的矩阵,从而导致公钥长度的增长。
(3)以Gentry-Sahai-Waters [12]为代表的、基于带误差学习或环上带误差学习困难问题构造的第3代全同态加密方案,此类方案的构造思想大致如下:
·方案的安全性最终归约到带误差学习或环上带误差学习的困难问题上。
·使用近似向量方法表示私钥,即用户的私钥实际就是密文的近似特征向量。
·密文的同态计算使用的是矩阵的乘法与加法运算。
这类方案被认为是目前最为理想的方案,它们不再需要密钥交换与模转换技术。
3 同态加密的应用
同态加密技术在分布式计算环境下的密文数据计算方面有着广泛而重要的应用。
(1)安全云计算与委托计算。同态技术在该方面的应用可以使得我们在云环境下,充分利用云服务器的计算能力,实现对明文信息的运算,而不会有损私有数据的私密性。例如医疗机构通常拥有比较弱的数据处理能力,而需要第三方来实现数据处理分析以达到更好的医疗效果或者科研水平,这样他们就需要委托有较强数据处理能力的第三方实现数据处理(云计算中心),但是医院负有保护患者隐私的义务,不能直接将数据交给第三方。在同态加密技术的支持下,医疗机构就可以将加密后的数据发送至第三方,待第三方处理完成后便可返回给医疗结构。整个数据处理过程、数据内容对第三方是完全透明的。
(2)远程文件存储。用户可以将自己的数据加密后存储在一个不信任的远程服务器上,日后可以向远程服务器查询自己所需要的信息,远程服务器用该用户的公钥将查询结果加密,用户可以解密得到自己需要的信息,而远程服务器却对查询信息一无所知。这样做还可以实现远程用户数据容灾。
(3)密文检索。密文检索有很多方案,例如文献[7]、[19-20]中介绍的就是基于同态加密技术设计的密文检索算法。我们仅介绍Gentry [7]用全同态加密方案实现密文检索算法: 用户将要检索的内容[f1,f2,…,fn]用公钥加密成密文[c1,c2,…,cn]。将搜索引擎的查询函数置为电路C,则搜素引擎就可以利用全同态算法中的[Evaluate]函数执行同态运算:
[CΣ=Evaluate(pk,Ci,(c1,c2,…,cn))](1)
其中[Ci∈C]用于计算输出的第
(4)安全多方计算协议设计的工具。所谓安全多方计算就是分别持有私有数据[x1,x2,…,xn]的[n]个人,在分布式环境中协同计算函数[f(x1,x2,…,xn)]而不泄露各方的私有数据。以同态技术支撑的密态数据计算不仅可以满足安全多方计算协议设计中保护各方隐私的需要,还能避开不经意传输协议而大大提升协议效率。近些年来,出现了很多高效的基于同态加密的安全多方计算协议,例如文献[6]、[21]。同态加密技术已经成为安全多方计算协议设计的一个强有力的工具[22]。
(5)电子选举。基于同态加密技术设计的电子选举方案,因在计票快捷与准确、节省人力与开支、投票的易用性等方面较传统投票方式有着无法企及的优越性,越来越受到人们的青睐。目前出现了很多基于同态的电子选举方案,像文献[23-24]中介绍的都是基于同态的电子选举方案。在此描述一下Damg?rd [23]方案:选民将自己的选票[vi∈{0,1}]加密[ci=Enc(vi)],选票中心统计部门(拥有密钥且可信)利用同态加密方案的同态性统计计算选票数[V=Dec(c1×c2×…cn)=v1+v2+…+vn]。
(6)其他方面的应用。同态加密技术在其他方面也有诸多应用,例如多方零知识证明、软件保护、聚合(同态)签名等。
4 同态技术存在的问题
综上所述,目前同态技术及其应用方面还存在以下几个重点问题需要我们进一步研究。
(1)只能实现单比特加密,如何高效地实现全同态加密有待进一步研究。
(2)大多基于未论证的困难问题,寻找可论证的困难问题依然是个摆在密码工作者面前的难题。
(3)大多只能达到IND-CPA安全,偶有能达到IND-CCA1安全,但还未见能达到IND-CCA2安全的,同态加密系统的安全性研究有待进一步提高。
(4)需要额外的消除噪音算法,依然不是自然同态,如何设计一个具有自然同态性的全同态加密方案依然是一个开问题。
(5)在安全云计算、安全多方计算、密态数据计算等领域的应用还处在初级阶段,有待于进一步地拓展;同时,在其他领域的相关应用也需要积极开拓。
5 结束语
随着分布式计算的普及,如何保护分布式计算环境下的用户隐私已经成为一个重要问题,密码学中的同态加密技术可以为分布式计算环境的用户隐私保护提供强有力的技术支撑。文章介绍了同态加密技术的研究现状及研究展望,并简单介绍了基于同态加密技术的密态数据计算在分布式计算中的各种应用。目前,同态加密方案在安全性方面大都只能达到IND-CPA安全,如何设计更高安全级别的同态加密方案依然需要进一步研究。全同态加密方案的构造还处于理论阶段,尚不能用于实际的密态数据计算问题,如何设计基于代数系统的(自然)全同态加密方案依然是未来研究的重点。同态加密技术支撑的密态数据计算在其他领域的应用有待进一步拓展。
参考文献
[1] RIVEST R L, ADLEMAN L, DDRTOUZOS M L. On Data Banks and Privacy Homomorphisms [J]. Foundations of secure computation, 1978, 4(11): 169-180
[2] RIVEST R L, SHAMIR A, ADLEMAN L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems [J]. Communications of the ACM, 1978, 21(2): 120-126. doi: 10.1145/359340.359342
[3] ELGAMAL T. A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms [M]. Advances in cryptology. Germany: Springer Berlin Heidelberg, 1985: 10-18. doi: 10.1007/3-540-39568-7_2
[4] OKAMOTO T, UCHIYAMA S. A New Public-Key Cryptosystem as Secure as Factoring [M]. Advances in Cryptology—EUROCRYPT'98. Germany: Springer Berlin Heidelberg, 1998: 308-318. doi: 10.1007/BFb0054135
[5] PAILLER P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes [M]. Advances in Cryptology—EUROCRYPT99. Germany: Springer Berlin Heidelberg, 1999: 223-238. doi: 10.1007/3-540-48910-X_16
[6] BONEH D, GOH E J, NISSIM K. Evaluating 2-DNF Formulas on Ciphertexts [M]. Theory of Cryptography. Germany: Springer Berlin Heidelberg, 2005: 325-341.doi: 10.1007/978-3-540-30576-7_18
[7] GENTRY C. Fully Homomorphic Encryption Using Ideal Lattices[C]//Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, 2009: 169-178. doi: 10.1145/1536414.1536440
[8] VAN D M, GENTRY C, HALEVI S, et al. Fully Homomorphic Encryption Over the Integers[M].Advances in Cryptology-EUROCRYPT 2010. Germany: Springer Berlin Heidelberg, 2010: 24-43
[9] BRAKERSKI Z, VALIKUNTANATHAN V. Fully Homomorphic Encryption from Ring-LWE and Security for Key Dependent Messages [M]. Advances in Cryptology-CRYPTO 2011. Germany: Springer Berlin Heidelberg, 2011: 505-524
[10] BRAKERSKI Z, GENTRY C, VAIKUNTANATHAN V. (Leveled) Fully Homomorphic Encryption without Bootstrapping [C]//Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, 2012: 309-325.doi: 10.1145/2090236.2090262
[11] BRAKERSKI Z. Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP [M]. Advances in Cryptology-CRYPTO 2012. Germany: Springer Berlin Heidelberg, 2012: 868-886. doi: 10.1007/978-3-642-32009-5_50
[12] GARG S, GENTRY C, HALEVI S, et al. Attribute-Based Encryption for Circuits from Multilinear Maps[M]. Advances in Cryptology-CRYPTO 2013. Germany: Springer Berlin Heidelberg, 2013: 479-499. doi: 10.1007/978-3-642-40084-1_27
[13] BRAKERSKI Z, VALIKUNTANATHAN V. Efficient Fully Homomorphic Encryption from (standard) LWE [J]. SIAM Journal on Computing, 2014, 43(2): 831-871
[14] CHEON J H, KIM J, LEE M S, et al. CRT-Based Fully Homomorphic Encryption over the Integers[J]. Information Sciences, 2015, 310: 149-162
[15] GOLDWASSER S, MICALI S. Probabilistic Encryption [J]. Journal of computer and system sciences, 1984, 28(2): 270-299
[16] I FERRER J D. A New Privacy Homomorphism and Applications[J]. Information Processing Letters, 1996, 60(5): 277-282. doi: 10.1016/S0020-0190(96)00170-6
[17] DOMINGO-FERRER J. A Provably Secure Additive and Multiplicative Privacy Homomorphism*[M]. Information security. Germany: Springer Berlin Heidelberg, 2002: 471-483
[18] MELCHOR C A, GABORIT P, HERRANZ J. Additively Homomorphic Encryption with D-Operand Multiplications [M]. Advances in Cryptology-CRYPTO 2010. Germany: Springer Berlin Heidelberg, 2010: 138-154.doi: 10.1007/978-3-642-14623-7_8
[19] LI J, WANG Q, WANG C, et al. Fuzzy Keyword Search over Encrypted Data in Cloud Computing[C]//INFOCOM, 2010 Proceedings IEEE, 2010: 1-5
[20] HU H, XU J, REN C, et al. Processing Private Queries Over Untrusted Data Cloud Through Privacy Homomorphism[C]// 2011 IEEE 27th International Conference on Data Engineering (ICDE), 2011: 601-612
[21] 李顺东, 王道顺. 基于同态加密的高效多方保密计算[J]. 电子学报, 2013, 41(4): 798-803
[22] BENDLIN R, DAMGARD I, ORLANDI C, et al. Semi-Homomorphic Encryption and Multiparty Computation[M]. Advances in Cryptology-EUROCRYPT 2011. Germany: Springer Berlin Heidelberg, 2011: 169-188
[23] CRAMER R, GENNARO R, SCHOENMAKERS B. A Secure and Optimally Efficient Multi-Authority Election Scheme [J]. European Transactions on Telecommunications, 1997, 8(5): 481-490
[24] DAMGARD I, JURIK M. A Generalisation, a Simplication and Some Applications of Paillier's Probabilistic Public-Key System[C]//Public Key Cryptography. Springer Berlin Heidelberg, 2001: 119-136.doi: 10.1007/3-540-44586-2_9

