基于RBF神经网络的永磁同步伺服电机控制系统

朱卫云,付东翔,葛懂林

(上海理工大学 光电信息与计算机工程学院,上海　200093)

基于RBF神经网络的永磁同步伺服电机控制系统

朱卫云,付东翔,葛懂林

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要针对永磁同步电机控制系统,建立其磁场定向控制数学模型。运用增量式数字PID的方法实现对PMSM的传统PID控制策略。在此基础上,借助RBF神经网络的学习能力,进行PID控制器参数的自适应整定,进一步改善PID控制器的性能。同时,为提高RBF网络性能,采用粒子群算法对网络进行优化。仿真表明,与传统PID控制比较,基于RBF的PID控制系统能提高PID控制器的性能,改善了PMSM控制系统的收敛速度和跟踪精度。

关键词PMSM;FOC;PID控制器;RBF网络;PSO算法

PMSM Control System Based on RBF Neural Network

ZHU Weiyun,FU Dongxiang,GE Donglin

(School of Optical-Electrical and Computer Engineering,University of Shanghai for

Science and Technology,Shanghai 200093,China)

AbstractThis paper first proposes the establishment of PMSM mathematical model.Then,the conventional PID control is discussed to achieve PMSM control system by using an incremental PID.The learning ability of RBF neural network offers adaptive PID controller parameter to improve the performance of PID controllers.The particle swarm optimization (PSO) is also proposed to improve the performance of RBF network in.The simulation results indicate that the mode control system based on RBF neural network can improve the performance of PID controller compared with conventional PID control with higher convergence speed and tracking accuracy of PMSM control system.

KeywordsPMSM;FOC;PID;RBF neural networks;PSO algorithm

永磁同步电机因其自身的结构及运行特别,在运动控制应用中起着重要作用,而被广泛应用于机器人、航空航天和国防军事等高精度速度和位置控制领域中。同步永磁电机装置在速度或者位置控制方面的整体性能,不仅取决于系统响应的快速和准确上,还取决于控制策略和算法。永磁同步电机的控制策略大致可分为以PID控制为主的经典控制策略,以直接转矩和自适应控制为主的现代控制策略,以神经网络、模糊数学和智能算法为主的智能控制策略[1]。经典的PID控制由于其具备简单的控制结构、设计简单和低功耗的优点,被广泛应用于PMSM(Permanent Magnet Synchronous Servo Motor)的控制中[2]。然而,经典的PID控制的比例系数、积分系数和微分系数依赖于PMSM控制过程的动态性能和实际经验,一旦固化就难以修改,而PMSM控制系统的负载变化、外部干扰、内部扰动等不确定因素引起整个控制系统的动态特性变化时,之前所给定的PID参数就无法达到较好的控制效果。

本文提出了一种基于RBF神经网络的PID控制系统,采用RBF网络的学习训练能力,去调节PID控制器的3项参数,从而改善了PID控制器的性能。通过仿真分析,得到常规PID控制算法和RBF神经网络PID控制算法的控制结果,并对两者的控制效果进行对比分析。这里提出RBF神经网络是一种3层前向网络,所有的隐含层神经元用高斯基函数作为激发函数来增加搜索空间。此外,RBF神经网络由输入到隐含层的映射是非线性的,而隐含层空间到输出空间的映射是线性的,从而大幅加快了学习速度,使得神经元对历史数据反应更灵敏。相比于常规PID控制算法,RBF神经网络PID控制系统无论是在收敛速度还是在跟踪精度方面均能得到明显的改善和加强。

1永磁同步伺服电机磁场定向控制原理

在旋转参考系中,永磁同步伺服电机的电学方程可表示为(1)。然后,根据磁场定向控制原理并将轴电流设置为零,得到永磁同步电机(2)与(3)动力学方程,以及负载的动力学方程(4)。用于仿真的永磁同步伺服电机的参数如式(1)所示[3-4]

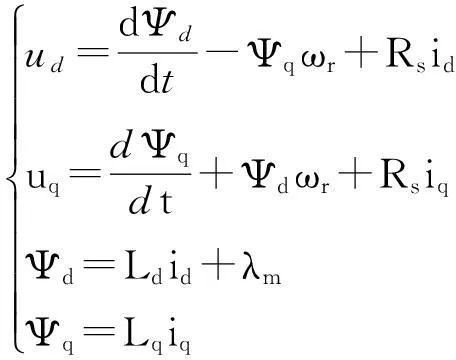
(1)

其中,ud,uq分别为d和q轴的电压分量;Ψd,Ψq分别为d,q轴的磁链;Rs为定子电阻;ωr=dθr/dt为电角度,其中θr为电机转子转角;id,iq分别为d,q轴的电流分量,且id=0;Ld,Lq分别为d,q轴的电感;λm为电压反馈常数

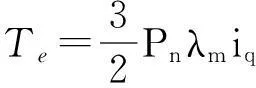
(2)

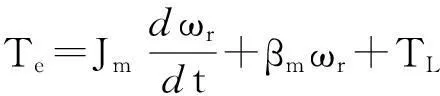
(3)

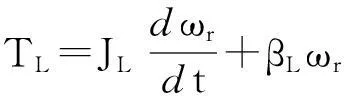
(4)

其中,Te为电磁转矩;TL为负载转矩;Pn为电机极对数;Jm和JL分别为电机和负载的转动惯量;βm和βL分别为电机的黏性阻尼系数。

由式(2)~式(4)及ωr=dθr/dt得到PMSM的二阶微分方程,如下

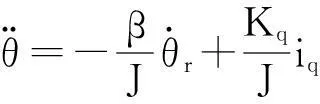
(5)

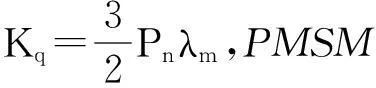
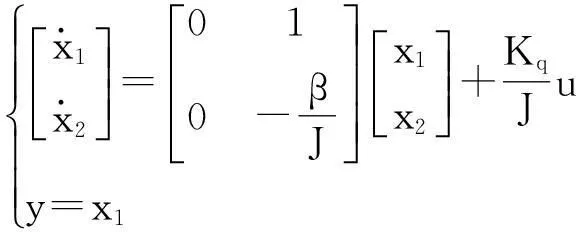
(6)

2RBF神经网络的PMSM控制系统

2.1　RBF网络PID控制模型

为有效地控制PMSM跟踪参考轨迹,这里提出了一个基于RBF神经网络智能控制算法[5],来实现PID的3项参数的实时在线修改。RBF神经网络PID控制流程,如图1所示。

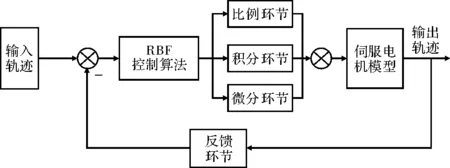
图1　RBF神经网络PID控制流程图

RBF神经网络PID的层数为3层,该网络组态的体系结构如图2所示,其包括输入层(第i层),隐含层(第j层)和输出层(第o层)[6]。

在RBF网络结构中采用Jacobian信息的辨识算法,x=[x1,x2,…,xn]T为网络的输入向量h=[h1,h2,…,hm]T。设RBF网络的径向基向量。其中n为输入层的节点数;m为隐含层的节点数;hj为高斯基函数为

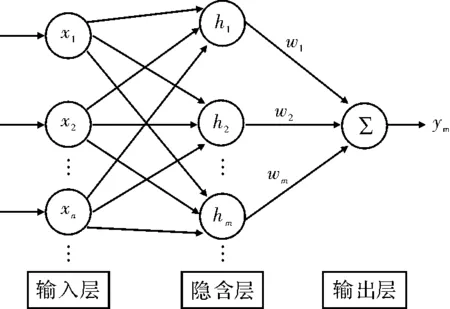
图2　RBF神经网络结构

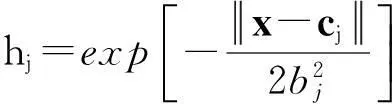
(7)

其中,网络的第j个节点的中心矢量为Cj=[cj1,cj2,…,cji,…,cjn],i=1,2,…,n。

设网络的基宽向量为

B=[b1,b2,…,bj,…,bm]T

bj为节点j的基宽度参数,且为>0的数。网络的权向量为

W=[w1,w2,…,wj,…,wm]T

辨识网络的输出为

ym(k)=w1h1+w2h2+…+wmhm

(8)

辨识器的性能指标函数为

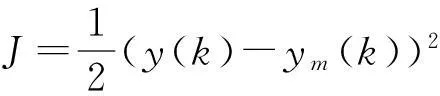
(9)

根据梯度下降法,输出权、节点中心及节点基宽参数的迭代算法如下

Δwj(k)=η(y(k)-ym(k))hj

(10)

wj(k)=wj(k-1)+Δwj(k)+α(wj(k-1)-wj(k-2))+β(wj(k-2)-wj(k-3))

(11)

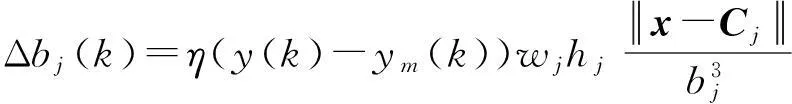
(12)

bj(k)=bj(k-1)+Δbj(k)+α(bj(k-1)-bj(k-2))+β(bj(k-2)-bj(k-3))

(13)

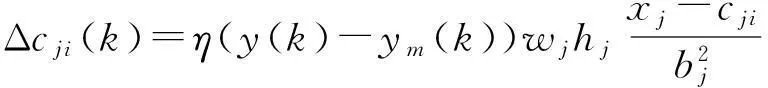
(14)

cji(k)=cji(k-1)+Δcji(k)+α(cji(k-1)-cji(k-2))+β(cji(k-2)-cji(k-3))

(15)

以上各式中,k为迭代运算次数;η为学习速率,0<η<1,α和β为动量因子,其值大于零,用于调整学习的收敛速度。

Jacobian阵算法为[6]

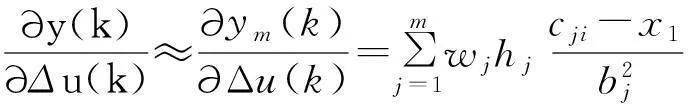
(16)

式中,x1=Δu(k);该算法表示对象的输出对控制输入变化的灵敏度信息。

2.2　RBF神经网络PID整定原理

PID控制器采用增量式PID控制算法对PMSM进行控制,其算法原理如下:PMSM的目标跟踪误差为

e(k)=yd(k)-y(k)

(17)

PID的3项输入为

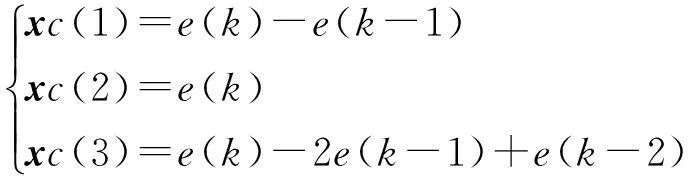
(18)

控制算法为

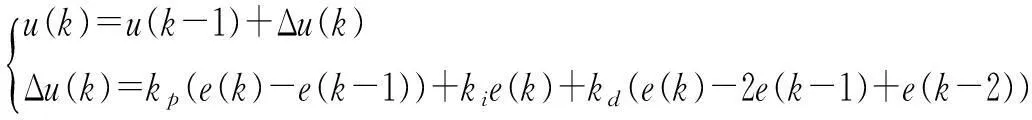
(19)

RBF神经网络PID在线训练算法采用有监督梯度下降法,其能量函数为

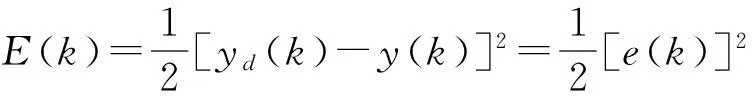
(20)

根据梯度下降法,PID 3项参数的在线更新调整为

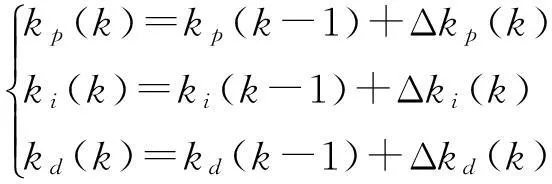
(21)

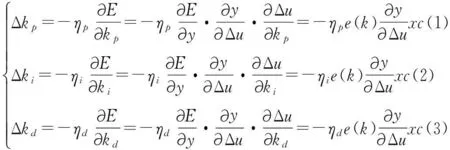
(22)

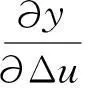
2.3　运用PSO算法调整RBF网络参数

如何选择学习速率η、ηp、ηi、ηd和动量因子α、β的值对网络性能有显著影响。为有效地训练RBF网络,将使用粒子群算法(ParticleSwarmOptimization,PSO)对网络进行优化,来提高这6个自适应学习速率。PSO技术是运用粒子群的方式找到最优解[7]。在PSO系统中,每个粒子代表一个候选解决问题的方法,且根据自身和邻居的经验来调整其位置,使其达到最优当前位置。PSO算法如下

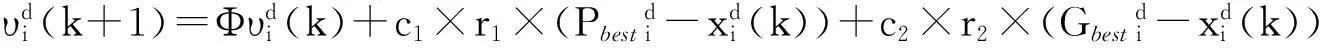
(23)

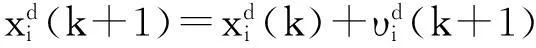
(24)

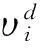
惯性权重Φ按照式(25)进行设置[8]

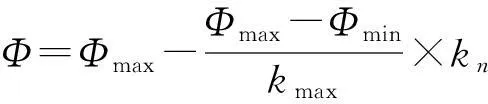
(25)

其中,kmax是算法允许的最大迭代次数;kn是迭代的当前次数值;Φ的值介于[Φmin,Φmax]。在本文中,惯性权重Φ的最大值和最小值分别取Φmax=0.7,Φmin=0.4。

3仿真结果与分析

基于以上的理论,在RBF神经网络中,输入层包括3个变量,即式(18)所示的PID的3项输入,输出层包括3个参数,PID控制器的kp、ki和kd这3个参数,根据误差的变化来实时调整PID的参数。为便于比较传统PID控制和RBF网络的PID控制,本文对这两个控制都进行了Matlab仿真[9],其Simulink模型如图3和图4所示。在仿真时,用于仿真的永磁同步伺服电机的参数如下:定子电感Ld=Lq=0.05 H,定子电阻Rs=1.5 Ω,转子惯量Jm=3×10-3kg·m2,电压反馈常数λm=0.175 V·s·rad-1,黏性阻尼系数βm=1×10-4N·m·rad-1·sec-1,极对数Pn=4。

图3中,在Simulink中找出相应的模块,搭建仿真系统。其中PID控制器的3个参数手动进行设置,Plant模块为伺服电机模型,其参数根据电机参数以及PMSM控制模型进行相应的设置,输入信号为正弦波形,采样时间为1 ms。并根据跟踪结果,反复调节PID控制器的3个参数,使其达到较好的跟踪效果。

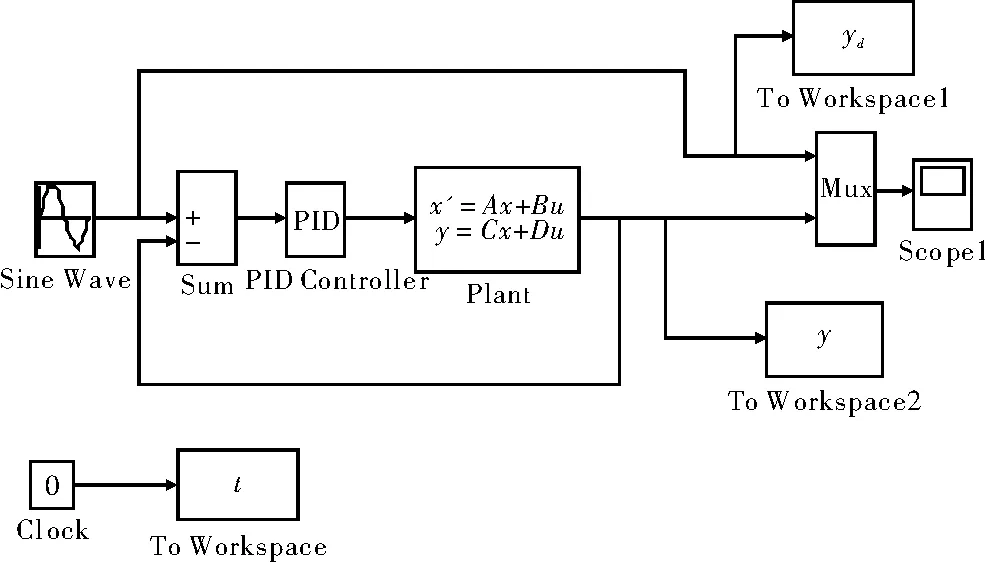
图3　基于传统PID控制的Simulink模型

图4的模型是在传统PID控制的基础上,将PID控制器用基于RBF神经网络的PID控制器代替,建立一个S函数来描述所用的控制算法。RBF_PID控制器为三输入/三输出的系统,该系统可根据跟踪效果,自适应地实时在线整定PID参数。输入信号为为正弦波形,采样时间为1ms。

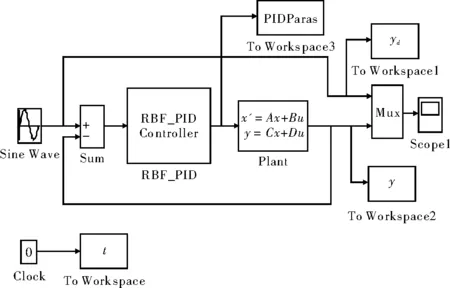
图4　基于RBF网络PID控制的Simulink模型

通过仿真,可得到PMSM轨迹跟踪曲线和参数的变化如图5所示。图5(a)是PID控制器和被控制对象级联后对目标轨迹信号的跟踪情况,且具有较好的跟踪效果。与图3所示的未校正的系统的跟踪情况相比,系统无稳态误差,调节时间短。系统的稳定性、快速性相当出色。图5(b)给出了参数kp、ki、kd的自适应整定轨迹,表明3个参数在较短的时间内就自适应地达到了稳定值kp=60、ki=0.5、kd=1,在线调节过程并不长。图5(c)给出了基于RBF网络PID控制系统在跟踪参考信号时,输出误差的变化情况。可见,系统的输出误差在很短的时间内减小到0,并最终稳定在0处,实现了对系统的误差控制。图5(d)给出了基于传统的增量式数字PID控制器在跟踪参考信号时,输出误差的变化情况。

比较图5(c)和图5(d)可看出,基于RBF神经网络PID控制的跟踪误差曲线明显小于传统的PID控制,且能快速使误差达到稳定。基于RBF神经网络整定PID参数的控制系统,PID参数可实时的获得,节约了不断调节所消耗的时间,并能改善控制系统的性能,提高了轨迹跟踪精度。相对于传统的PID控制,RBF神经网络整定PID具有一定的优越性。

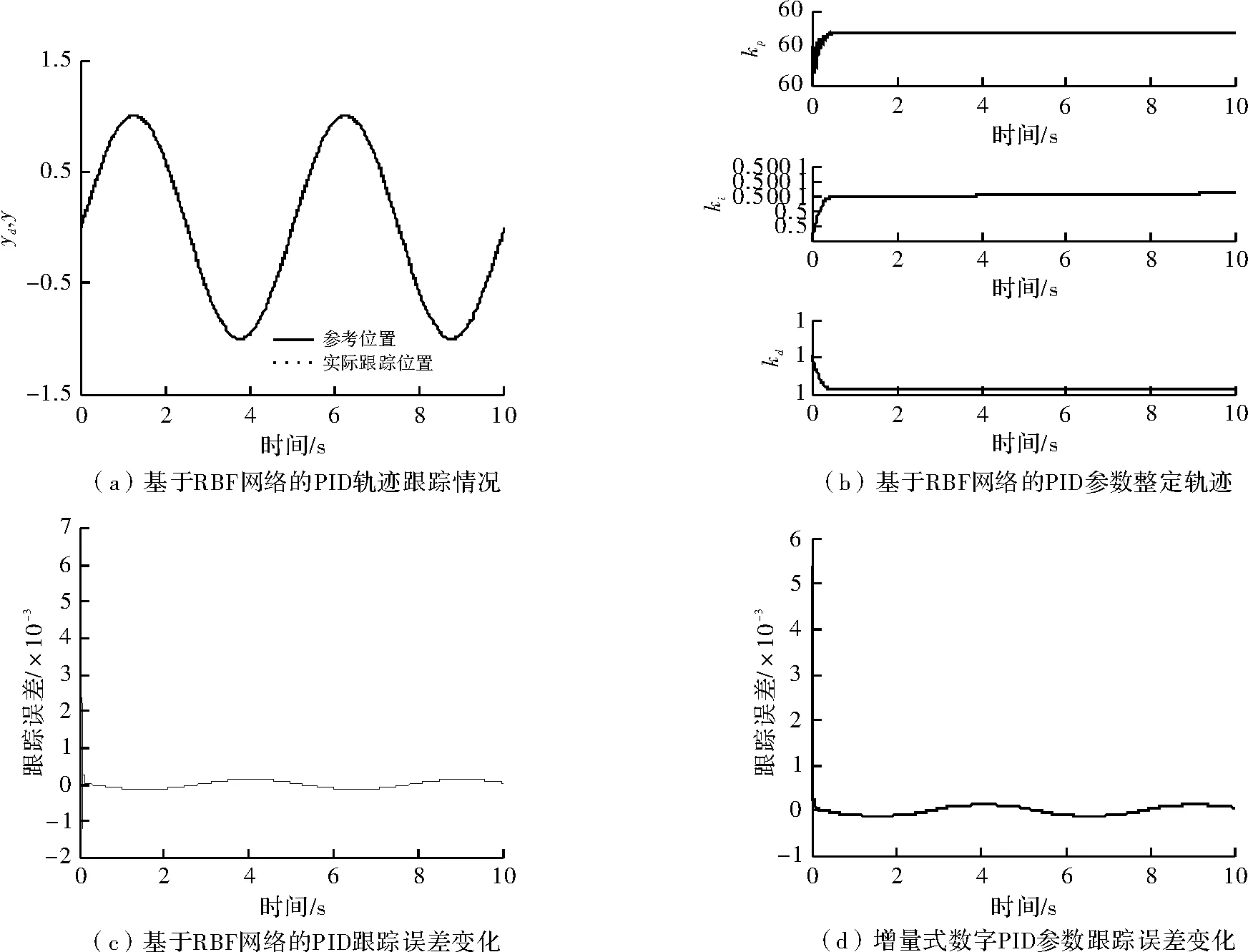
图5　RBF神经网络整定PID参数仿真结果

4结束语

本文采用RBF神经网络所具有的任意非线性表达能力,通过对系统性能的学习来实现具有最佳组合的PID控制,且可不断自适应地调整PID参数,使得PMSM伺服系统满足稳定性、快速性的要求[10]。

仿真实验表明,所提出的基于RBF神经网络的PID控制策略能根据PMSM伺服系统的实时在线情况,来调整系统控制量的输出,使系统的快速性能和稳定性能均得到大幅优化。所以,适用于工业应用领域PMSM伺服控制系统的跟踪控制。

参考文献

[1]冯国楠.现代伺服系统的分析与设计究[M].北京:机械工业出版社,1990.

[2]张嗣瀛,高立群.现代控制理论[M].北京:清华大学出版社,2008.

[3]尔联洁.自动控制系统[M].北京:航空工业出版社,1994.

[4]汤新舟.永磁同步电机的矢量控制系统[D].杭州:浙江大学,2005.

[5]刘金琨.先进PID控制Matlab仿真[M].3版.北京:电子工业出版社,2010.

[6]舒怀林.PID神经元网络及其控制系统[M].北京:国防工业出版社,2006.

[7]Kennedy J,Eberhart R.Particle swarm optimization[C].Paris:Proceedings of IEEE International Conference,Neural Networks,1995.

[8]Wai R J,Lee J D,Chuang K L.Real-time PID control strategy for maglev transportation system via particle swarm optimization[J].IEEE Transactions on Industrial Electronics,2011,58(2):629-646.

[9]夏玮.Matlab控制系统仿真与实例详解[M].北京:人民邮电出版社,2008.

[10]马立新,徐镇乾,范洪成,等.永磁同步电机伺服系统控制最优化方法[J].电子科技,2015,28(5):154-157.

作者简介:朱卫云(1987—),女,硕士研究生。研究方向:嵌入式系统,伺服驱动系统,工业机器人。付东翔(1971—),男,副教授,硕士生导师。研究方向:嵌入式系统,伺服驱动系统。

收稿日期:2015- 06- 03

中图分类号TM351

文献标识码A

文章编号1007-7820(2016)01-161-05

doi:10.16180/j.cnki.issn1007-7820.2016.01.043