具有媒体报道的传染病模型稳定性

刘俊利，刘璐菊

(1.西安工程大学 理学院，陕西 西安 710048；2.河南科技大学 数学与统计学院,河南 洛阳 471023)



具有媒体报道的传染病模型稳定性

刘俊利1，刘璐菊2

(1.西安工程大学 理学院，陕西 西安 710048；2.河南科技大学 数学与统计学院,河南 洛阳 471023)

摘要：研究了一类具有媒体报道和潜伏期的传染病模型，得到了模型的基本再生数。利用线性化方法和Liapunov函数，分析了无病平衡点的全局渐近稳定性和正平衡点的局部渐近稳定性。如果不考虑疾病引起的死亡率，则正平衡点是全局渐近稳定的。最后，模型的持久性也得以证明。

关键词：媒体报道；全局稳定性；基本再生数；持久性

0引言

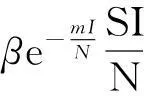
1建立模型

把总人口N(t)分成3个仓室：易感者S(t)，潜伏者E(t)和染病者I(t)。假设：A为常数输入率;μ为自然死亡率因数；σ为从潜伏者到染病者的转化因数；δ为染病者的恢复率因数；α为因病死亡率因数。β(I)为接触率，β(I)=μ1-μ2f(I)，其中，μ1为易感者与染病者的最大接触率，μ2为由于大众媒体对染病者的报道而减少最大接触率，假设μ1≥μ2且

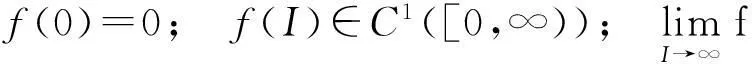
(1)

(2)

显然，总人口N(t)满足方程：

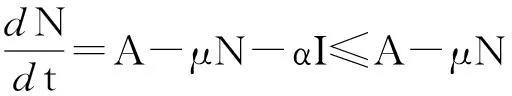
(3)

因而

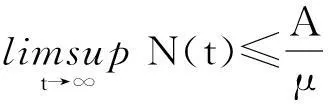
从生物学角度考虑,仅在集合

中研究模型(2)。易证集合D为模型(2)的正向不变集。

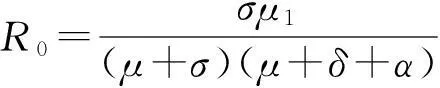
2无病平衡点的全局渐近稳定性

证明模型(2)在P0处的特征方程为：

(λ+μ)[λ2+(2μ+δ+α+σ)λ+(μ+σ)(μ+δ+α)-σμ1]=0。

(4)

显然，2μ+δ+α+σ>0成立。且当R0<1时，有(μ+σ)(μ+δ+α)-σμ1>0，无病平衡点P0局部渐近稳定；当R0>1时，有(μ+σ)(μ+δ+α)-σμ1<0，特征方程(4)有正根，无病平衡点P0不稳定。

下面证明当R0≤1时，无病平衡点P0是全局渐近稳定的。构造Liapunov函数：

L(t)=σE+(μ+σ)I，

则有

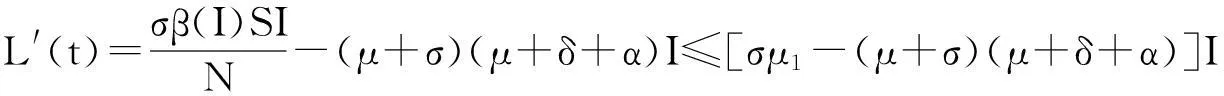
当R0≤1时，则L′(t)≤0，当且仅当I=0时，L′(t)=0。由Lasalle不变集原理[10]可知：P0为全局渐近稳定的。

3正平衡点的稳定性及模型的持久性

假设模型(2)存在正平衡点P*(S*,E*,I*)，令模型右边等于0，解得：

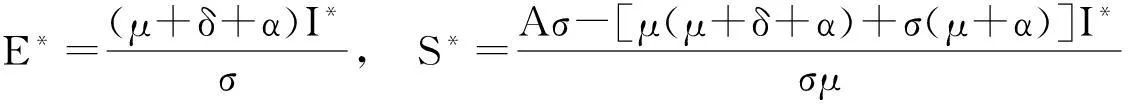
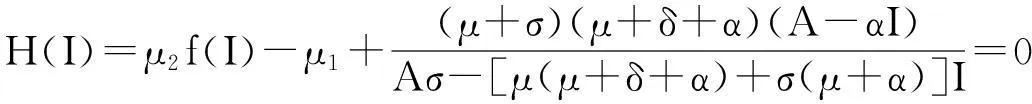
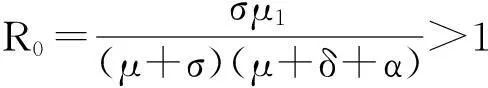
证明通过计算，模型(2)在正平衡点P*(S*,E*,I*)处的特征方程为:

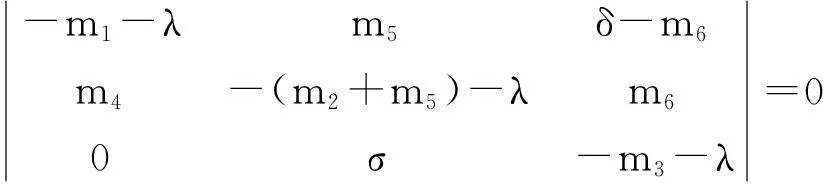
即

λ3+c1λ2+c2λ+c3=0，

(5)

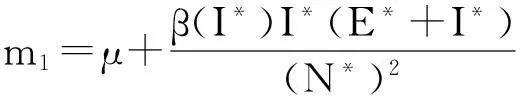
(6)

因此，

m1m2m3-σδm4-μm2m3=m4(m2m3-σδ)>0。

经过计算和化简得:

c1c2-c3=(μ+m5)[m2m3+m1(m2+m3)+μm5]+

(m2+m4)[m1(m2+m3)+μm5]+

m3m5(m3+m4+m5)+m3(m1m3+μm5)+

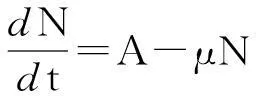
(7)

由Bendixson-Dulac定理知：系统(7)在第一象限不存在闭轨线，所以(E*,I*)全局渐近稳定。由模型(2)的第一个方程得S(t)的极限方程为：

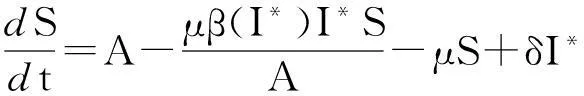
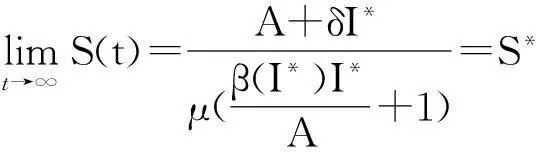
利用文献[10]中的结果可以证明模型(2)的持久性，证明过程与文献[11]类似。

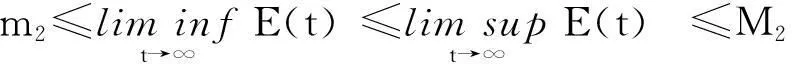
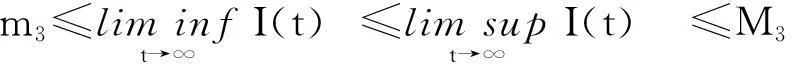
4结论

本文研究了一类具有媒体报道和潜伏期的传染病模型，得到了模型的基本再生数R0。R0完全决定了模型的动力学行为：当R0≤1时，无病平衡点全局渐近稳定；当R0>1时，无病平衡点不稳定，正平衡点局部渐近稳定，且模型持久。如果不考虑染病者的因病死亡因素，则正平衡点是全局渐近稳定的。

参考文献：

[1]CUI J A,SUN Y,ZHU H P.The impact of media on the control of infectious diseases[J].Journal of dynamics and differential equations,2008,20(1):31-53.

[2]PRASAD S G,DHA J.Dynamics of an SEQIHRS epidemic model with media coverage,quarantine and isolation in a community with pre-existing immunity[J].Journal of mathematical analysis and applications,2015,421(2):1651-1672.

[3]刘玉英,肖燕妮.一类受媒体影响的传染病模型的研究[J].应用数学和力学,2013,34(4):399-407.

[4]曹磊,周文,张道祥.一类受接种疫苗和媒体报道影响的传染病模型[J].南通大学学报(自然科学版),2014,13(4):77-81.

[5]胡新利,杨亚莉,赵惠文,等.媒体报道对禽流感(H7N9)传播影响的研究[J].西北大学学报(自然科学版),2014,44(4):525-528.

[6]TCHUENCHE J M,DUBE N,BHUNU C P,et al.The impact of media coverage on the transmission dynamics of human influenza[J].BMC public health,2011,11(suppl 1):S5.

[7]CUI J A,TAO X,ZHU H P.An SIS infection model incorporating media coverage[J].Rocky mountain journal of mathematics,2008,38(5):1323-1334.

[8]SUN C J,YANG W,ARINO J,et al.Effect of media-induced social distancing on disease transmission in a two patch setting[J].Mathematical biosciences,2011,230:87-95.

[9]VAN D D P,WATMOUGH J.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Mathematical biosciences,2002,180:29-48.

[10]THIEME H R.Persistence under relaxed point-dissipativity(with application to an endemic model)[J].SIAM journal on mathematical analysis,1993,24(2):407-435.

[11]LIU J L,WU J H,ZHOU Y C.Modeling disease spread via transport-related infection by a delay differential equation[J].Rocky mountain journal of mathematics,2008,38:1525-1540.

文献标志码：A

中图分类号：O175.1

DOI:10.15926/j.cnki.issn1672-6871.2016.02.018

文章编号：1672-6871(2016)02-0088-04

收稿日期：2015-05-06

作者简介：刘俊利(1981-),女,河南濮阳人,副教授,博士,硕士生导师,主要从事传染病动力学等方面的研究.

基金项目：国家自然科学基金项目(11101323,11101127)；陕西省自然科学基础研究计划基金项目(2014JQ1038)