基于物理干扰模型的延迟最小化数据汇聚算法

王 亚，李光顺

(曲阜师范大学 信息科学与工程学院，山东 日照 276800)

基于物理干扰模型的延迟最小化数据汇聚算法

王 亚，李光顺

(曲阜师范大学 信息科学与工程学院，山东 日照 276800)

在无线传感器网络(Wireless Sensor Networks,WSN)中,如何快速、准确地将传感器收集的数据汇聚给汇聚节点是数据汇聚中的一个重要问题。早期，研究者主要研究了协议干扰模型下的数据汇聚问题。由于协议干扰模型不能精确计算节点之间的干扰，而物理干扰模型可以克服这个缺点。因此，针对物理干扰模型中的延迟最小化数据汇聚问题，提出了一个Hexagon-AS算法，得到了一个延迟上界O(m)，其中m为覆盖网络的六边形的层数。该算法首先用六边形单元格将网络覆盖，然后对单元格染色，最后对具有相同颜色的单元格进行并发调度。仿真结果表明，Hexagon-AS算法比现有的算法有更小的延迟。

无线传感器网络；数据汇聚；物理干扰模型；延迟

0 引 言

无线传感器网络是一个自组织网络，由部署在受监测区域内的大量低成本、低功耗，具有感知、数据存储、数据处理和无线通信能力的传感器节点组成。其目的是协作地采集、处理和传输网络覆盖区域中被感知对象的信息[1-2]。在传感器传递数据的过程中，如果原始数据可以被聚合且只有聚合值被传送到汇聚节点，称它为数据汇聚[3-4]。数据汇聚是无线传感器网络的典型传输形态[5-6]。经过汇聚，中间节点传递给下一跳节点的数据大小仅是接收数据的一小部分[7]。

在数据汇聚中，延迟最小化数据汇聚是众多研究者关注的问题之一[8]。目前，协议干扰模型下的数据汇聚已取得了大量成果。但协议干扰模型在计算干扰时仅计算了邻近区域的干扰，忽略了网络中其他节点的干扰。而物理干扰模型将网络中所有并发传输节点产生的干扰都考虑进来，可以更精确地计算节点间的干扰。

1 相关工作

数据汇聚自从在文献[9]中被提出以后，便得到了广泛关注。在文献[10-14]中提出了若干基于协议干扰模型的集中式延迟最小化数据汇聚算法。Chen等在文献[10]中证明了延迟最小化数据汇聚是NP难问题，并给出了一个(Δ-1)近似算法。其中Δ为网络中节点的最大度。随后Huang等设计了一个基于极大独立集的集中式算法[13]，得到的延迟为23R+Δ-18,R为网络半径。但是，集中式算法不具有可扩展性[15]，因此，后来研究者们开始研究分布式算法来解决这个问题。目前，在分布式算法中取得的最好的延迟界为O(Δ+R、)，R'低于网络半径，满足R'≤R≤D≤2R、，D是网络直径[14]。

Li等研究了物理干扰模型下的延迟最小化数据汇聚[16]，得到的延迟界为O(R+Δ)。之后Li设计了一种分布式算法[17]，取得了一个有效的延迟界O(K)，其中K是网络中最长链路长度和最短链路长度的比率对数。而文献[17]中假设节点的功率足以覆盖网络中最远的两个节点，这个假设太过理想。文中提出了一种Hexagon-AS算法，并证明了算法的有效性。

2 网络模型

文中考虑由n个传感器节点V={v1,v2,…,vn}和一个汇聚节点v0组成的无线传感器网络，其中vi表示节点i，ei表示节点i的能量。这些节点随意分布在一个圆形区域A中，A=πr2，r为网络的区域半径。汇聚节点位于该区域的中心。假设网络中任何两个节点之间的距离至少为1。令T=(V,E)表示以汇聚节点为根的数据汇聚树，V={v0,v1,…,vn}，E={ei,j|i≠j},ei,j表示从节点vi到节点vj的一条链路。

问题是构造一棵数据汇聚树T，网络中的传感器沿着这棵树将收集到的数据传递给汇聚节点，使所用的时隙总数最少。在数据传输过程中，需要满足物理干扰模型的条件，即信号干扰加噪声比(SINR)：

其中，vi和vj分别表示发送节点和接收节点；Pi表示节点vi的功率；‖vi-vj‖表示节点vi和节点vj之间的欧几里得距离；vk为与vi并发传输的其他节点；N0为背景噪声；α为路径损耗因子，其值为[2,6]；β为SINR阈值，通常大于1。

3 网络划分

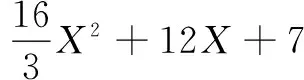
图1 数据汇聚

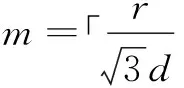
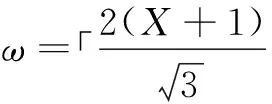
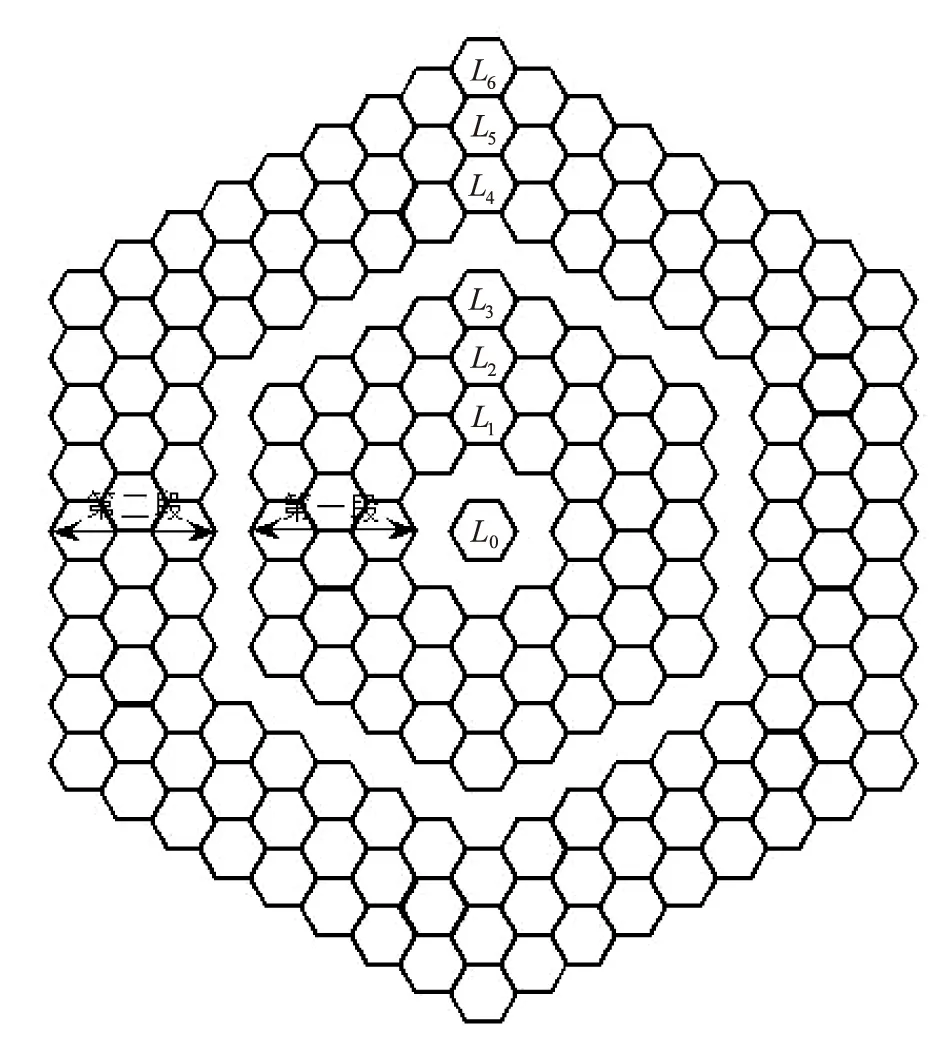
图2 层和段的划分

4 算法描述

算法的主要思想如下：

第一阶段，单元格内的调度。首先在每个单元格内选出一个具有最大能量emax=max{ei|vi∈ci,j}的节点，作为该单元格内的局部汇聚节点，单元格内的其他节点都在给定的时隙内，将收集到的数据传送给局部汇聚节点。为避免节点间的干扰，给单元格染色，具有相同颜色的单元格需要满足它们之间的距离足够远。文中设定它们之间的距离至少为2(X+1)d，如图1(b)所示。

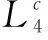
算法1：HAS 。

Input: Node setVwith sinkV0

Output:Data aggregation treeTand link scheduleS

1.t=0,d=1,T=φ,S=φ,St=φ,E=φ,E′=φ,E″=φ,E‴=φ;

2.Cover the network with cells of side lengthdand color them

3.whilel>0 do

5. cells with coloriselect one node which has the max energy as the local aggregation nodeAij

6. nodes in the cellscijtransmit its data toAijin the specify time soltt

8.St=St∪E′;

9.t=t+1;

10.E=E∪E′ ;

11. for each segment

12. calling LTL;

13. forL=m-ω+1 to 0 do

14. calling STS;

15.end while;

16.T=T∪E;

17.S=S∪St

18. returnTandS；

算法1实现数据汇聚树的构造以及链路调度。算法2、3分别用于实现层到层的调度和段到段的调度。

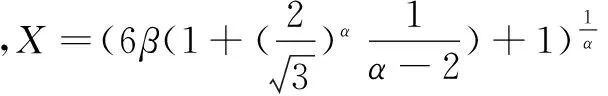
算法2：LTL 。

Input:Local aggregation nodesAij

Output:Time slottandSt

2. local aggregation nodeAijselect one latest local aggregation node from thei-1 layer;

3. send its data toAi-1,j;

5.St=St∪E″ ;

6.l=l-1;

7.t=t+1;

算法3：STS。

Input:local aggregation nodeAij

Output:Time slottandSt

2. local aggregation nodeAijlocated in theLlayer select one neareast local aggregation nodeAghfrom theL-ωlayer;

3. send its data toAgh;

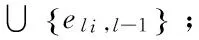
5.St=St∪E‴;

6.t=t+1;

7.L=L-ω;

5 分 析

这一部分首先对算法的正确性进行分析，然后证明算法的有效性。

5.1 正确性

定理1：基于六边形的分布式数据汇聚调度算法构造了一棵数据汇聚树，且该算法可以在物理干扰模型下正确地对链路进行调度。

证明：算法共三个阶段。第一阶段是单元格内的数据汇聚，每个单元格内的节点都在指定的时隙向局部汇聚节点发送数据，且仅发送一次。第二阶段，每个段的下层局部汇聚节点都将得到的汇聚值传递给段首的局部汇聚节点，各层的局部汇聚节点也仅发送一次数据。第三阶段，由外到内每段的段首向上一段的段首发送汇聚值，直到将每段的数据都汇聚到汇聚节点。纵观三个阶段，每个阶段都由不同的节点发送数据，且每个节点都仅在本阶段发送一次，故形成了一棵数据汇聚树。根据文献[17]可知，在物理干扰模型中，相距2(X+1)d的两个单元格之间可以干扰自由地传输数据，因此定理成立。

5.2 有效性

定理2：Hexagon-AS算法的数据汇聚延迟上界为O(m)。

证明：首先证明如果单元格中任何两个节点之间的距离都至少为1，那么在一个边长为1的六边形中至多有七个节点，使用文献[11]中的一个结果来证明。假设U是半径为r的圆盘中节点间距离至少为1的节点集合，那么

边长为1的六边形可以被包含在一个半径为1的圆盘中，所以

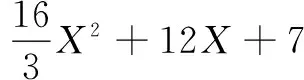
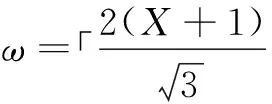
证明完成。

文中算法构造了一棵数据汇聚树，实现了数据的有效汇聚，并得到了一个延迟上界O(m)。

6 仿 真

对Hexagon-AS算法进行仿真，并将结果与文献[17]中的Cell-AS算法进行比较。假设网络部署在一个半径为100m的圆形区域中，随机产生0至1 000个传感器节点，这些节点随意分布，节点间的距离至少为1。设N0的值设为0.1，α为3和4，β为2、4和6。仿真用C语言编写，在Matlab7.0中运行。

首先比较不同α和β值下Hexagon-AS算法的数据汇聚延迟。图3(a)表示当α=3时汇聚延迟随β值的变化情况。观察发现随β的增大汇聚延迟逐渐增大，这是因为当β增大，发送节点的功率不变时，网络中并发传输的节点之间的干扰减小，这意味着并发传输的节点数减少，因此汇聚时间增大。图3(b)表示当α=4时汇聚延迟随β值的变化情况，与图3(a)有相同的变化趋势。

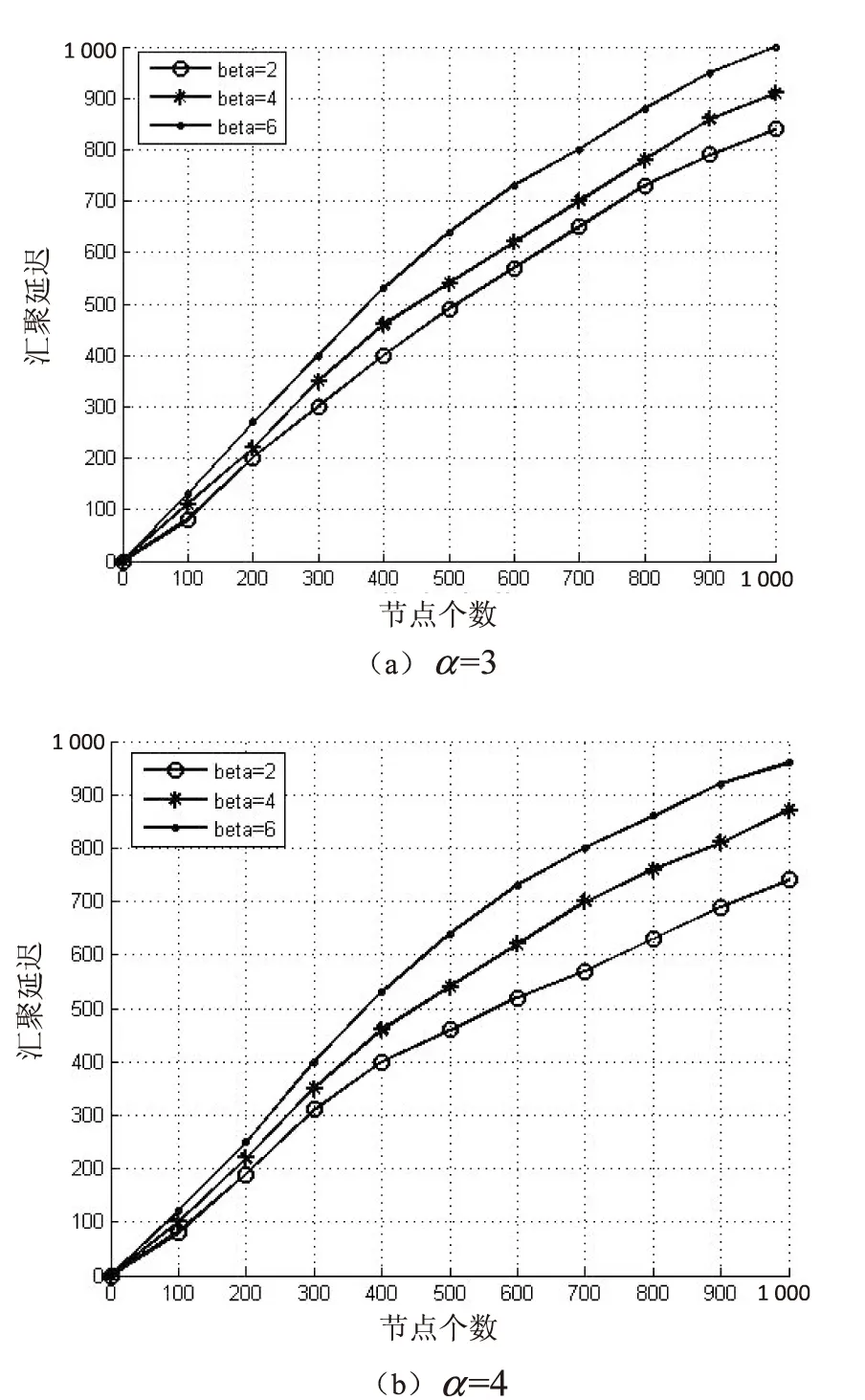
图3 不同α下的汇聚延迟

图4给出的是Hexagon-AS算法和Cell-AS算法的比较。图4(a)表示当α=3时两种算法得到的汇聚延迟时间，图4(b)表示α=4时的比较结果。结果显示，文中算法比Cell-AS算法有更小的延迟时间。

7 结束语

文中分析了基于物理干扰模型的数据汇聚延迟问题，设计了一个分布式延迟最小化数据汇聚算法—Hexagon-AS。首先将网络用六边形单元格覆盖，然后对单元格进行分层、分段，最后对具有相同颜色的单元格进行并发调度，得到了一个O(m)的延迟上界。经理论分析和仿真实验证明，该算法是有效的。下一步将引入CSMA机制，以期得到更高的数据传输成功概率。

图4 延迟比较

[1] 白永祥.一种LEACH路由协议算法的改进与分析[J].通信技术，2015，48(9):1062-1067.

[2] 张建明,宋迎清,周四望,等.无线传感器网络中数据汇聚技术的研究[J].计算机应用，2006,26(6)：1273-1278.

[3]ChenS,WangY,LiXY,etal.Order-optimaldatacollectioninwirelesssensornetworks:delayandcapacity[C]//Procofthe6thannualIEEEcommunicationssocietyconferenceonsensor,meshandadhoccommunicationsandnetworks.Rome:IEEEPress,2009:1-9.

[4]YuB,LiJ,LiY.Distributeddataaggregationschedulinginwirelesssensornetworks[C]//ProcoftheIEEEinternationalconferenceoncomputercommunications.RiodeJanein:IEEEPress,2009:2159-2167.

[5] 朱红松,孙利民,徐勇军,等.基于精细化梯度的无线传感器网络汇聚机制及分析[J].软件学报，2007，18(5)：1138-1151.

[6] 王辛果,张信明,陈国良.时延受限且能量高效的无线传感器网络跨层路由[J].软件学报,2011,22(7):1626-1640.

[7] 彭 刚，曹元大，钟伟军，等.无线传感器网络的数据汇聚机制[J].计算机工程，2006，32(6)：115-117.

[8] 刘文彬，李香宝，付 沙，等.无线传感器网络中的改进数据聚集调度算法[J].计算机工程，2014,40(1):93-97.

[9]BoukercheA.Algorithmsandprotocolsforwirelesssensornetworks[M].[s.l.]:Wiley&Sons,2008.

[10]ChenX,HuX,ZhuJ.Minimumdataaggregationtimeprobleminwirelesssensornetworks[C]//ProcofMSN’05.Wuhan:IEEEPress,2005:133-142.

[11]WanPJ,HuangSCH,WangL.Minimum-latencyaggregationschedulinginmultihopwirelessnetworks[C]//ProcofMOBIHOC’09.NewYork:ACMPress,2009:185-194.

[12]XuX,LiXY,MaoX.Adelay-efficientalgorithmfordataaggregationinmultihopwirelesssensornetworks[J].IEEETransactionsonParallelandDistributedSystems,2011,22(1):163-175.

[13]HuangCH,WanP,VuCT.Nearlyconstantapproximationfordataaggregationschedulinginwirelesssensornetworks[C]//Procof26thIEEEinternationalconferenceoncomputercommunications.[s.l.]:IEEEPress,2007:366-372.

[14]LiY,GuoL,PrasadSK.Anenergy-efficientdistributedalgorithmforminimum-latencyaggregationschedulinginwirelesssensornetworks[C]//ProcofIEEEICDCS’11.Genovn:IEEEPress,2010:827-836.

[15] 郑国强,李建东,周志立.多跳无线传感器网络的高能效数据收集协议[J].软件学报,2010,21(9):2320-2337.

[16]LiXY,XuX,WangS.Efficientdataaggregationinmulti-hopwirelesssensornetworksunderphysicalinterferencemodel[C]//ProcofMASS’09.Macau:IEEEPress,2009:353-362.

[17]LiH,WuC,HuaQS,etal.Latency-minimizingdataaggregationinwirelesssensornetworksunderphysicalinterferencemodel[J].AdHocNetworks,2011,12:52-68.

A Data Aggregation Algorithm of Latency-minimizing Based on Physical Interference Model

WANG Ya，LI Guang-shun

(College of Information Science and Engineering,Qufu Normal University,Rizhao 276800,China)

In the Wireless Sensor Networks (WSN),how to quickly and accurately gather the data collected by sensors to sink node is very important in data aggregation.In the early,researchers mostly focus on the problem of data aggregation under protocol interference model which can’t accurately compute interference between nodes,but the physical interference model can overcome this shortcoming.Therefore,considering that latency-minimizing data aggregation in the physical interference model,a Hexagon-AS algorithm is proposed,and an upper bound of the latencyO(m)isachieved,mofwhichisthelayerofthehexagoninthenetworks.Firstly,thealgorithmproposedcoversthenetworkwithhexagoncells,thencoloringthecells,finallymakingcellswiththesamecoloronconcurrent.SimulationshowsthatHexagon-AShassmallerlatencythantheexistingalgorithm.

wireless sensor networks;data aggregation;physical interference model;latency

2015-10-23

2016-01-27

时间：2016-06-22

国家自然科学基金资助项目(61373027)；山东省优秀中青年科学家奖励基金项目(BS2014DX005)

王 亚(1991-)，女，硕士研究生，研究方向为无线传感器网络；李光顺，副教授，研究方向为计算机网络与通信。

http://www.cnki.net/kcms/detail/61.1450.TP.20160622.0844.024.html

TP

A

1673-629X(2016)07-0080-05

10.3969/j.issn.1673-629X.2016.07.017