一种基于网线传感器网络的数据补全算法

让 涛，王立松

(南京航空航天大学 计算机科学与技术学院，江苏 南京 210016)

一种基于网线传感器网络的数据补全算法

让 涛，王立松

(南京航空航天大学 计算机科学与技术学院，江苏 南京 210016)

无线传感网络在人类社会生活中的应用越来越广泛。同时，无线传感网络在应用中也存在诸多问题，其中包括数据异常和和数据丢失的问题。由于分布环境的影响，加上无线传感网络自身的局限性，如何有效地实现丢失数据的补全成为了重要的研究课题。传统的无线传感网络数据补全方法针对缺失数据，根据时间或空间的相关性，主要从其单一属性进行缺失估计，而不是从整体上对数据样本进行多个属性的缺失估计。据此，文中提出一种基于OptSpace的改进算法—Ioptspace算法，同时考虑时间相关性和空间相关性，把传感网络收集的数据规范化为矩阵，并从整体上对其进行补全。实验结果表明，与线性插值算法、基于空间相关性算法相比，所提出的Ioptspace数据补全算法估计准确率更高，具有更好的效果。

无线传感网；数据异常；数据缺失；数据补全；Ioptspace算法

1 概 述

无线传感器网络(Wireless Sensor Network)是由大量传感器节点所构成。WSN能够协作地执行信息的实时监测、感知和采集任务，并对数据进行处理，传送到用户终端[1]。由于传感器的电源和存储能力的限制，加上部署环境的特殊性，经常存在数据的异常、错误和丢失等问题，导致无线传感器网络在应用中可信度降低。于是一系列数据异常检测方法[2-3]、数据补全方法应运而生。文中提出一种改进的Ioptspace数据补全算法。

由于无线传感器网络的传感器节点属性、分布环境等的限制[4]，网络中不可避免地会出现感知数据的缺失问题。缺失数据是指数据源中某条记录存在一个或多个属性值为空，也就是不完整数据[5]。如果直接丢弃缺失数据，不做任何分析，很可能得到不完整的原始数据信息；如果不对缺失数据进行补全，则无法被用到现有的一些分析工具中，如决策树、K平均聚类算法等[6]。不对缺失数据进行适当的处理，会增加运算难度，降低分析结果的准确性和可靠性，甚至造成严重的后果。

常用的缺失数据处理方法有如下四种：

(1)将存在缺失数据的记录直接丢弃[7]。这种方法对原始数据信息不作任何分析，破坏原始数据信息的完整性，影响分析结果甚至导致错误,造成网络资源的浪费。

(2)用全局变量或属性的平均值替换所有的缺失数据，并作为属性的一个新值[7]。这种方法适用于数据稳定的情况，考虑了感知数据在时间维度上连续变化的特点。

(3)缺失数据的K-近邻估计方法[6]，用全局变量或属性均值代替缺失值，不能有效地处理感知数据的非平稳变化。K-近邻算法考虑了感知数据的空间相关性(在规定阈值内，由于数据的空间相关性，邻居节点之间的数据值相差甚小)，用其邻居节点的数据来估计缺失节点的值。

(4)缺失数据的模型预测方法[7]，这种方法分析已收集的正确数据的内在关系，并以此建立预测模型。缺失数据可以根据预测模型进行预测估计。

对于WSN的数据缺失问题，HalatchevM等在文献[8]中给出WARM算法。该算法根据关联规则找到出现数据缺失节点的关联节点，再用该关联节点的数据值替换缺失值。在WARM的改进算法—CARM算法[9]中，JiangN等利用关联规则分析流数据，根据多个数据源节点找出其频繁模式，以此模式估计缺失值。WARM算法和CARM算法虽然能有效地处理离散数据，但其对关联规则中的阈值设定依赖性大，因此未能普遍应用。针对WARM算法和CARM算法的局限性[10]，学者们先后提出三个数据补全算法，包括线性插值(LIN)算法、空间相关性(MR)算法以及LM算法。LIN算法依据的是数据的时间相关性，MR算法考虑了数据的空间相关性。LM根据数据的具体情况选择LIN算法或者MR算法。文献[11]提出了如何用最少数据建立数据估计模型的算法，虽然能节省资源，但降低了估计的准确度。文献[12]提出将WSN划分成簇图，利用最少的传感器节点的观测值，实现对该监测区域内的任意位置进行数值估计。此算法主要研究在不考虑感知数据的估计误差情况下，实现使用最少的传感器来得到感知数据。文献[13]中指出，对于较短时间间隔内平稳变化的感知数据，线性插值算法[10]能实现较好性能的估计。然而，对于非线性相关的数据样本的缺失数据，基于时空相关性的缺失数据补全算法具有更好的补全效果。

针对部分数据已知的感知信息，KeshavanRH等[14]提出一种OptSpace矩阵补全算法，进行重新构建。据此，文中提出一种改进算法——Ioptspace算法。通过把传感器网络收集的数据样本当成矩阵从整体上对其进行补全，而不是对某一属性或某几个数据属性分别进行补全，同时结合了时间相关性和空间相关性进行分析。实验和分析结果表明，Ioptspace算法可以有效地解决WSN缺失数据的补全问题。

2 OptSpace算法原理

假设存在一个秩为r(r≪m,n)的m×n的矩阵M，m×r的矩阵U，r×n的矩阵V以及r×r的对角阵Σ，满足以下关系：

M=UΣVT

(1)

式中：U的列是MM*的特征向量；V的列是M*M的特征向量；Σ对角矩阵中的非零元素是MM*或M*M中的非零特征值的平方根。

为了表示收集数据样本中的未缺失的或者正常的那些数据属性，假设有一个矩阵E，它是矩阵M的一子集，如式(2)所示。

(2)

ME是包含M子集E的矩阵，未知的元素用0填充，元素0表示缺失或异常数据，具体如式(3)所示。

(3)

子集E是随机的并且不唯一。确定ME后，对ME进行奇异值分解，可以得到式(4)：

(4)

其中，σi(σ1≥σ2≥…≥0)是奇异值，与特征值类似。

在矩阵ME的基础上得到矩阵Tr(ME)，奇异值是递减排列并且减少的特别快，所以Tr(ME)的元素可以通过前r大的奇异值近似描述。大多数情况下，全部奇异值之和的99%以上是由前10%甚至1%的奇异值的和占据，如式(5)所示：

(5)

其中：(mn/|E|)是缩放因子，它可以表示大多数缺失数据的情况；Tr(ME)是ME在秩为r的集合上的正交投影。

通过对Tr(ME)进行奇异值分解的多次迭代过程来减少Tr(ME)和M的误差，直至误差的给定要求被满足。误差表示为：

(6)

3 Ioptspace算法

3.1 Ioptspace算法描述

OptSpace算法主要思想：已知部分数据集，据此来构造新矩阵，然后计算新矩阵的补全数据与缺失数据的误差值，最后重复迭代过程，直至原始矩阵和新矩阵的误差值满足设定的阈值范围。

在OptSpace算法的基础上，提出一种改进算法—Ioptspace算法。在Ioptspace算法中，无线网传感器节点的感知数据集转化为矩阵来处理，矩阵的行属性表示数据属性，矩阵的列属性表示数据样本。OptSpace算法的补全值与缺失值的误差计算公式如式(2)所示，其含义为：误差值表示的是真实值误差与缺失数据属性的平方和。在OptSpace算法中，误差值并不能反映感知数据某一属性的真实值与估计值之间的误差，而仅仅考虑达到给定条件的情况和感知数据属性的误差。

Ioptspace算法误差的表达如式(7)：

(7)

为了保证数据属性估计值的正确性，误差必须满足式(3)中所示的两个条件：数据属性自身的误差与数据属性整体的误差。

Ioptspace算法函数形式为：

[XSY]=Ioptspace(M_E,r,niter,tol1,tol2)

其中：S为一个r×r的矩阵；X为一个size(M_E,1)×r的矩阵；Y为一个size(M_E,2)×r的矩阵；M_E为含缺失数据的样本矩阵，0表示缺失处数据；niter为最大迭代次数，默认为50；tol1,tol2为迭代的终止条件;r为重建矩阵的秩。

Ioptspace算法伪代码如下：

(1)niter=50;tol1=1e-6;tol2=1e-6

(2)r=guessRank(M_E);

/*初始化对角阵与左/右奇异向量*/

(5)[XSY]=svds(Tr(M_E),r)

(6)i=1; /*循环次数记录*/

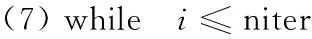
/*调整对角阵与左/右奇异向量*/

(8)X=X+w;Y=Y+z;

S=getoptS(X,Y,Tr(M_E),E)

/*定义误差表达式*/

(9)a=norm((XSY'-M_E).*E,'fro');

err1=a/sqrt(|E|);

(10)err2=sqrt(((XSY')ij-(M_E)ij)2)

/*比较误差与终止条件直到小于终止条件*/

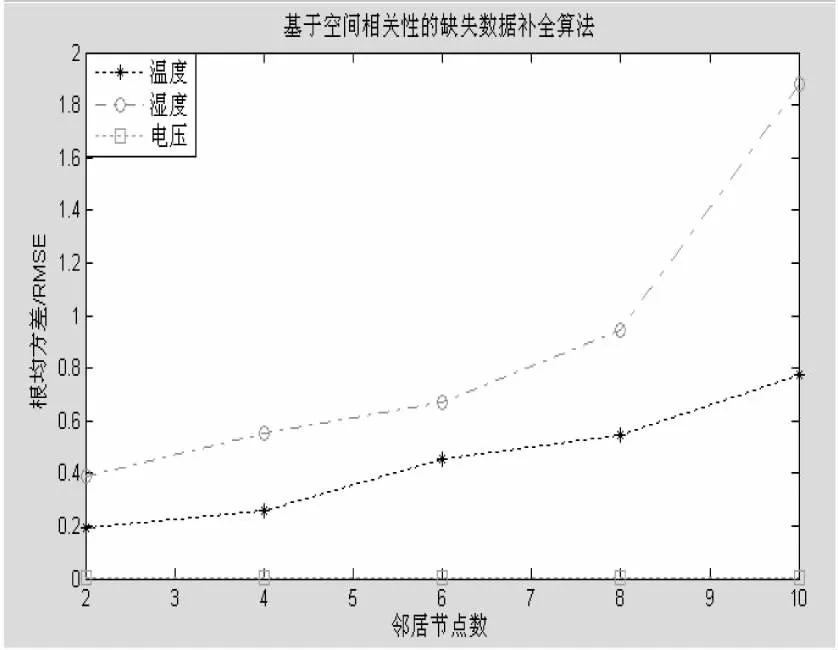
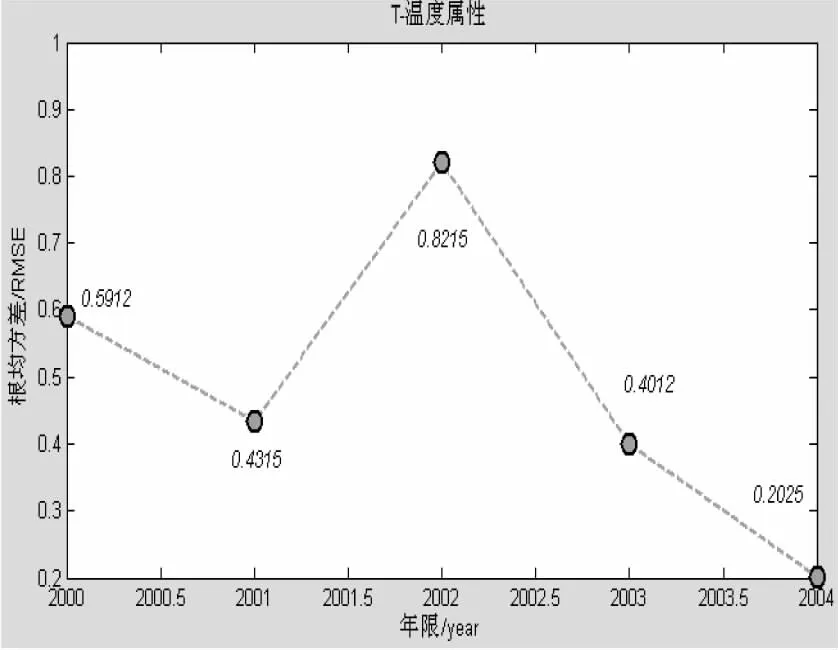
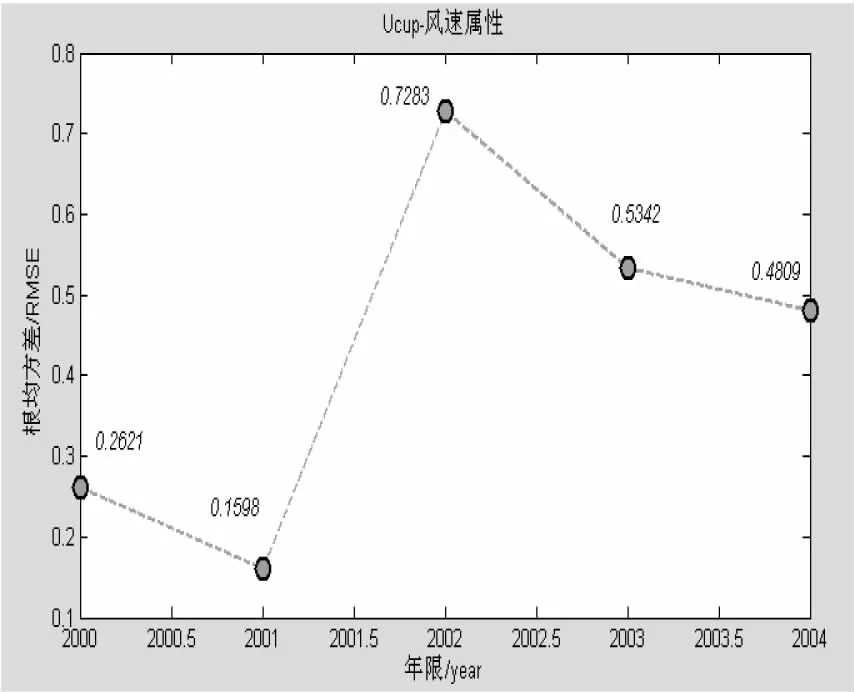
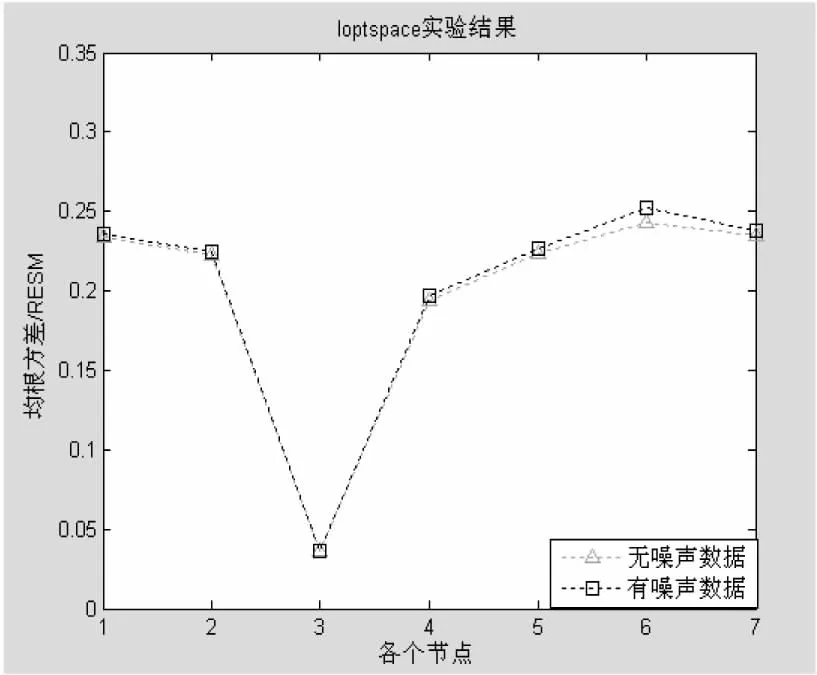
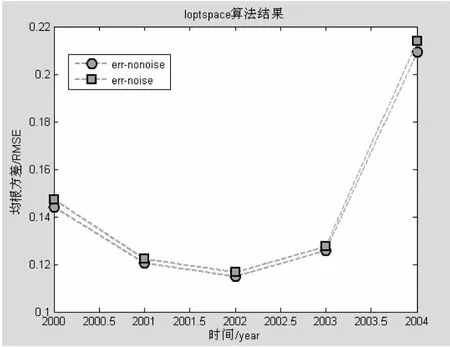
(11)if( err1

(12)break

(13) end /*if结束*/

(14)end /*while结束*/

3.2 Ioptspace算法性能分析

不同的数据补全算法的性能不同，文中选取了两种比较方法进行性能分析，即线性插值算法和基于空间相关性的数据补全算法。假设数据的维度为n，数据的样本数为m，缺失数据的样本数为k。线性插值算法的时间复杂度最低，为O(k)，实现简单。然而，基于空间相关性的缺失数据补全算法，由于其数值估计要考虑邻居节点的数值，故算法的效率依赖于邻居节点的个数，也与每个邻居节点的距离等因素相关。若当前节点的邻居节点数为l，则基于空间相关性的缺失数据补全算法的时间复杂度为O(knl)。Ioptspace算法既考虑时间相关性和空间相关性，又从整体上对数据缺失数据进行估计，故其时间复杂度最高，为O(mn+m2)。

如上所述三种算法各有其优缺点，适用范围也不相同。

如果数据样本主要特点表现为时间相关性，那么就使用线性插值算法进行缺失数据估计；数据样本主要特点表现为空间相关性，那么就使用基于空间相关性的缺失数据补全算法进行缺失数据估计；如果数据样本的整体属性都有缺失，并且数据样本的时间相关性特点与空间相关性特点都不明显，那么就可以采用Ioptspace算法实现缺失数据的补全。

4 实 验

根均方差(RootMeanSquareError，RMSE)可以反映算法对缺失数据的补全效果。当根均方差较小时，对缺失数据的估计值较准确，误差更小。

文中采用根均方差作为对比实验的度量标准，计算式如下：

(8)

4.1 实验数据

文中在公用数据集上进行实验分析，包括伯克利实验室布置的无线传感器网络环境收集的数据集以及巴西圣塔伦Tapajos国家森林高塔上采集的气象数据。对于伯克利实验室数据，分别从电压、湿度、温度和亮度四个属性进行实验分析。对于巴西圣塔伦的气象数据样本，分别从T64、T40、T10、T2、press、h2o_64m、Usonic_64、WD_64、Ucup_64和Ucup_50共十个属性进行实验分析，并针对不同的对比方法提取不同的属性组进行实验。考虑到线性插值算法的时间相关性特点，提取了T64、T40、T10、T2、press、h2o_64m、Usonic_64、WD_64、Ucup_64和Ucup_50共十个属性。同时，针对时间维度上的均匀变化，分别提取数据样本对每个属性的缺失进行数据补全估计。考虑到数据的空间相关性，基于空间相关性的缺失数据补全算法提取了两组数据属性：T64、T40、T10、T2属性组和Ucup_64、Ucup_50、Ucup_40属性组。同时，依据邻居节点的当前数据值，估计当前节点在此刻的数据值。文中所提的Ioptspace算法不仅考虑时间相关性和空间相关性，同时对缺失数据进行整体属性的缺失估计。

气象数据来自于塔上67 m高度处的气象数据，主要包括热量土壤、水分、水蒸气、二氧化碳和呼吸通量等。由于这些变量大部分没有人工填充，可以计算出净生态系统交换量、二氧化碳的存储量以及总初级生产力等。变量中仅对二氧化碳存储量进行填充，以防止净生态系统的交换失衡。气象数据样本分布在2000年6月29日至2004年3月11日期间，采样周期较长，近三年半的时间。一共采集到64 992条数据记录，其中每隔30 min采集一次。数据记录主要包括温度、湿度、热量、二氧化碳浓度等属性，多达50个。在属性方面，文中分别选取了不同高度处的温度、压力、水蒸气、风速等属性进行实验。而在时间方面，在2000-2004年间，每年选取相关的数据样本进行实验。

4.2 对比实验

对于伯克利实验室数据，采用线性插值算法进行实验。实验选取节点35的邻居节点1、2、33、34、36、37，以其为感知数据样本。以温度、湿度和电压三个属性分别进行缺失数据的估计。对于节点37，分别对不同采样间隔和不同缺失数据个数两种情况进行实验。伯克利实验数据每隔31 s采集一次数据样本，其采样周期很短。因此，线性插值算法分别以0.5 min、2 min、4 min、6 min、8 min和10 min六种不同的采样间隔的数据样本进行实验，所有的数据样本均包含200个缺失数据。另外，缺失数据个数从25到100，依次以15递增，采样间隔均为31 s。由于采样间隔很短，因此受到温度和湿度的变化的影响很小。实验显示，线性插值算法的根均方差较小，估计效果比较准确。

对于伯克利实验数据样本和巴西圣塔伦的气象数据样本，采用基于空间相关性的缺失数据补全算法进行实验。此算法考虑空间相关性，利用感知数据的空间相关性进行缺失数据估计。图1～3分别展示了在伯克利实验数据样本和巴西圣塔伦的气象数据样本的实验结果。

图1 伯克利实验数据样本的空间相关性算法实验结果

如图1所示，从2到10，依次以2递增地选取邻居节点数。实验结果表明，空间相关性算法与线性插值算法相比，实验结果较差。由于传感器节点的地理位置相对较远，导致空间关联性较弱。另外，数据样本的采样间隔仅为31 s，导致样本本身的时间关联性更强。因此，与线性插值算法相比，基于空间相关性的缺失数据补全算法的估计效果较差。

对于巴西圣塔伦的气象数据样本，分别选取了温度和风速两个属性进行实验。实验中，分别对2 m、10 m、40 m和60 m高度的空气温度进行实验，表示为T2、T10、T40和T60。以节点T40为中心节点，其余为邻居节点，邻居节点数目为3。对2000-2004年的数据样本，依据空间相关性采用邻居节点的数值估计中心节点的数据值，分别统计实验结果，如图2所示。对于风速属性，Ucup_40、Ucup_50和Ucup_64分别表示为杯型测力计在40 m、50 m、64 m高度处测得的风速大小，实验结果如图3所示。

图2 温度属性的空间相关性缺失

从图2中可知，实验利用T60、T10和T2的数值估计T40的数值，在2000-2004年间，每年数据样本的检测误差分别为0.591 2、0.431 5、0.821 5、0.401 2和0.202 5，总体样本的平均检测误差率为0.489 5。基于空间相关性的缺失数据补全算法比线性插值算法得到的检测误差更大。由于选取的距离间隔大：从2 m、10 m、40 m到60 m，空间距离增大导致空间相关性降低，使得检测误差比线性插值算法的检测结果大。

图3 风速属性的空间相关性缺失

从图3可知,实验采用属性Ucup_64和Ucup_40的数值估计得到Ucup_50的数值。如图所示，2001-2004年数据样本的检测误差分别为0.262 1、0.159 8、0.728 3、0.534 2和0.480 9，其中2001年的检测误差最小，2002年的检测误差最大，总体数据样本的平均误差为0.433 1。同时，相比于温度属性的检测误差，风速属性的检测误差在整体上更小。无论是邻居节点的数目，还是邻居节点的空间距离，风速属性都比温度属性要小。因此，风速属性的检测误差更小，检测效果更好。

图4为Ioptspace算法在伯克利实验数据样本的缺失数据补全效果。

图4 伯克利实验数据样本的Ioptspace算法实验结果

实验中，Ioptspace算法选取节点35为中心节点，节点1、2、33、34、36和37为邻居节点，并对数据样本属性进行整体补全。实验结果显示，与线性插值算法和基于空间相关性的算法相比，Ioptspace算法的估计误差更小；同时，对无噪声数据和有噪声数据，Ioptspace算法都很有效，估计效果都很好。

图5为巴西圣塔伦气象数据的Ioptspace算法实验结果。

图5 巴西圣塔伦气象数据的Ioptspace算法实验结果

实验中，Ioptspace算法选取2000-2004年间的数据样本。在无噪声和有噪声的条件下，对10个不同的属性T64、T40、T10、T2、press、h2o_64m、Usonic_64、WD_64、Ucup_64和Ucup_50分别进行实验。图5中带方块虚线展示了有噪声条件下的实验结果，带六边形虚线则展示了无噪声条件下的实验结果。

4.3 实验结果分析

实验结果显示，随着采样间隔的增大，线性插值算法的每个数据属性的RMSE都在逐渐增大，即每个属性的估计误差逐渐在增大。因为线性插值算法是基于时间相关性的，随着采样间隔的变化，属性间的时间关联性也会发生变化。因此，缺失数据属性的估计误差也会受到影响。

另外，随着邻居节点数的增加，基于空间相关性算法的估计误差值也逐渐增大。空间相关性算法是基于空间相关性的，中心节点的邻居节点增多，使得位置较远的节点与中心节点的数据空间关联性减弱，从而影响到当前节点的数值估计，使误差变大。

线性插值算法针对单个属性进行缺失估计，而基于空间相关性的缺失数据补全算法，主要针对空间位置相邻的几个数据属性进行缺失值估计。不同于此两种算法，Ioptspace算法将感知数据集转化为矩阵来处理，矩阵的行属性表示数据属性，矩阵的列属性表示数据样本。另外，Ioptspace算法通过把传感器网络收集的数据样本当成矩阵从整体上对其进行补全，而不是对某一个或某几个属性分别进行补全，实现同步地对不同的属性的缺失值进行估计。

实验结果表明，与线性插值算法和基于空间相关性的算法相比，Ioptspace缺失数据补全算法的检测误差更小，检测的正确率更高，整体检测结果更好。同时，在无噪声和有噪声条件下的数据样本实验结果显示，Ioptspace算法都很有效，估计效果都很好。

5 结束语

文中提出了一种改进的WSN缺失数据的补全Ioptspace算法，同时考虑时间相关性和空间相关性，把感知数据集转化为矩阵来处理，并从整体上对其进行补全，而不是对某一属性或某几个数据属性分别进行补全。实验结果表明，与线性插值算法、基于空间相关性算法相比，所提出的Ioptspace数据补全算法具有更高的精确度和正确率，实验效果更好。

Ioptspace算法虽然可以比较正确地对缺失数据进行估计，但是仍存在局限性。在重组矩阵的秩不唯一和样本矩阵不满足奇异值分解的情况下，该算法的效果不够理想。在将来的工作中，会进行深入的探讨研究，以期找到解决方法。

[1] 魏巨巍.面向无线传感器网络的高效异常检测算法研究[D].南京:东南大学,2011.

[2] Markou M,Singh S.Novelty detection:a review-part 1:statistical approaches[J].Signal Processing,2003,83(12):2481-2497.

[3] Hodge V J,Austin J.A survey of outlier detection methodologies[J].Artificial Intelligence Review,2004,22(2):85-126.

[4] 徐苏娅.基于无线传感器网络的数据异常检测和补全算法研究[D].南京:南京航空航天大学,2012.

[5] 沈 雪.基于贝叶斯方法的缺失数据补全研究[D].重庆:重庆大学,2011.

[6] Troyanskaya O,Cantor M,Sherlock G,et al.Missing value estimation methods for DNA microarrays[J].Bioinformatics,2001,17(6):520-525.

[7] Kantardzic M.Data mining concepts,models,methods,and algorithms[M].2nd ed.[s.l.]:[s.n.],2011.

[8] LeGruenwald M H.Estimating missing values in related sensor data streams[C]//Proceedings of the 11th international conference management of data.[s.l.]:[s.n.],2005:83-94.

[9] Jiang N,Gruenwald L.Estimating missing data in data streams[M]//Advances in databases:concepts,systems and applications.Berlin:Springer,2007:981-987.

[10] 潘立强,李建中,骆吉洲.传感器网络中一种基于时-空相关性的缺失值估计算法[J].计算机学报,2010,33(1):1-11.

[11] Li Y,Ai C,Deshmukh W P,et al.Data estimation in sensor networks using physical and statistical methodologies[C]//Proc of 28th international conference on distributed computing systems.[s.l.]:IEEE,2008:538-545.

[12] Zhang H,Moura J M F,Krogh B.Estimation in sensor networks:a graph approach[C]//Proceedings of the 4th international symposium on information processing in sensor networks.[s.l.]:IEEE Press,2005.

[13] 潘立强,李建中.传感器网络中一种基于多元回归模型的缺失值估计算法[J].计算机研究与发展,2009,46(12):2101-2110.

[14] Keshavan R H,Montanari A,Oh S.Matrix completion from a few entries[J].IEEE Transactions on Information Theory,2010,56(6):2980-2998.

A Novel Algorithm for Completion of Missing Data in Wireless Sensor Networks

RANG Tao，WANG Li-song

(School of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

In recent years,wireless sensor networks are widely used to promote the development and progress of human social life.However,the limitations of WSN and the influence of distribution environment conditions result in that the perception data of WSN exists problems about abnormality and loss which seriously affect the WSN application.The full complement of missing data still needs to be resolved.In wireless sensor networks,the method used in data completion mainly considers about the time correlation or spatial correlation,and only can estimate a single missing data attribute,but it fails to estimate multiple attributes of data samples.For this problem,an improved Ioptspace algorithm based on OptSpace is put forward to solve the problem.This algorithm,simultaneously considering both time and spatial correlation,fully complements data collected by the sensor network as a matrix.Experiments show that compared with the data completion method of linear interpolation and spatial correlation,the estimation effect and accuracy of Ioptspace algorithm is better.

wireless sensor networks;data anomaly;data missing;data completion;Ioptspace algorithm

2015-07-29

2015-11-05

时间：2016-05-05

国家“973”重点基础研究发展计划项目(2014CB744900,2014CB744903)

让 涛(1990-)，男，硕士研究生，研究方向为航空电子系统安全性研究、无线传感网络；王立松，博士，副教授，研究方向为航空电子系统安全性研究、无线传感网、数据管理技术。

http://www.cnki.net/kcms/detail/61.1450.TP.20160505.0817.058.html

TP301.6

A

1673-629X(2016)05-0040-06

10.3969/j.issn.1673-629X.2016.05.009