Massive MIMO上行系统能效资源分配算法
江爱珍,曾桂根
(南京邮电大学,江苏 南京 210003)
Massive MIMO上行系统能效资源分配算法
江爱珍,曾桂根
(南京邮电大学,江苏 南京 210003)
研究了在认知无线电Ad Hoc网络(CRAHNs)中基于大规模多输入多输出(Massive MIMO)上行系统的能效资源分配算法。簇头采用迫零(ZF)接收,且考虑在电路功率消耗、各节点的最小数据速率以及最大发射功率的情况下,建立基于能效下界的非凸优化模型。根据分数规划的性质,将能效最优化问题中分数形式转化为减式形式,从而利用凸优化求解最优接收天线数和各节点发射功率来获得最大能效。仿真结果表明,所提算法在能效上近似最优值,能够满足各节点最小数据速率及最大功率的约束条件,且能以较小的迭代次数收敛到最优能效性能。
Massive MIMO;能效;资源分配;上行系统;分数规划;CRAHNs
0 引 言
认知无线电自组网络(CRAHNs)是一种具有频谱感知功能的分布式多跳移动自组网络,无固定中心节点,每个节点都具备路由、转发功能,组网方便快捷[1]。因此CRAHNs在军事、民用救灾、抢险、货运码头等场合获得了广泛应用。如图1所示,CRAHNs中节点主要包括手持设备(单天线节点,SN)、单兵背负式设备(多天线节点,MN)和车载设备(大规模天线节点,MM),其中SN和MN作为普通节点(以下简称节点),MM作为簇头。此时,簇头和节点可分别看作是蜂窝网中的基站和用户。因此,虽然目前CRAHNs网络下大规模MIMO的研究成果很少,但可类比蜂窝网下的大规模MIMO问题。
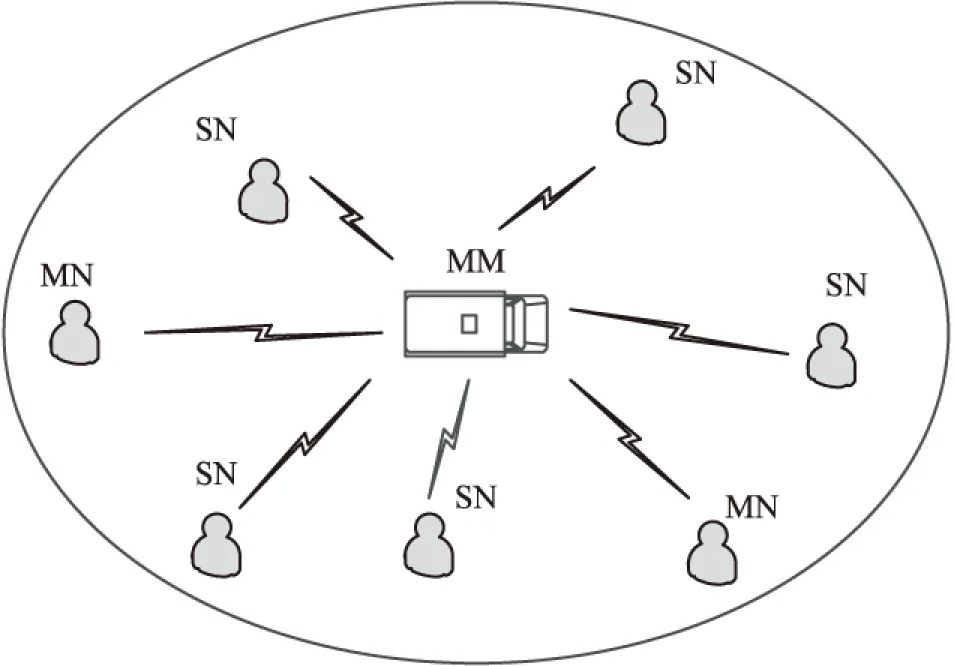
图1 系统模型
大规模多输入多输出(Massive MIMO)技术在增强频谱和能量效率方面具有很大优势[2-8],目前蜂窝网下的Massive MIMO技术已被高度关注[9-13]。文献[5]研究推导了多用户Massive MIMO系统在上行分别采用最大比合并(MRC)、迫零(ZF)和最小均方误差(MMSE)检测时的容量下界。文献[6]在采用MRC和ZF检测的情况下,研究了只考虑最大系统容量时,完全已知和不完全已知信道状态信息(CSI)的上行链路导频长度、导频功率和数据功率分配。文献[7]研究了多节点Massive MIMO系统下行的能效资源分配,在考虑用户服务质量(QoS)时,提出了用户速率分配、基站子载波和天线分配的策略,并给出了相应的迭代算法。文献[9]通过设计Massive MIMO系统的发送帧结构来提高频谱效率。
文中在CRAHNs中应用Massive MIMO技术来提高网络的通信性能并降低能量消耗。假设接收端完全已知信道状态信息(CSI),文中主要研究簇头和节点之间的上行资源分配算法,将各节点的最大发射功率以及QoS需求作为约束条件,提出了基于能效下界的目标函数,根据分数规划的性质,将目标函数中的分数问题转化为减式最优化问题,从而降低计算复杂度。
1 系统模型及问题描述
1.1 系统的吞吐量下界
文中主要研究CRAHNs中Massive MIMO的上行系统,簇头配置M根天线,已有研究表明,多用户MassiveMIMO系统的信道快衰落系数满足零均值,且是独立同分布(independentandidenticallydistributed,i.i.d.)[14]。因此下面都采用瑞利衰落信道。
首先讨论MN与簇头间通信问题的处理。为方便分析说明,假设MN只配置有2根天线,且2根天线联合编码,功率消耗为2P,此时MN的速率为:
(1)
而2根自主单天线SN功率消耗分别为P时,总速率为:
其中,hi是第i个SN节点(或i根天线)到簇头的信道矩阵;N0是噪声方差。
根据式(1)、(2)可知,RMN=Rsum,因此在上述假设条件下,MN与簇头间的通信可等效成2个SN节点与簇头间的通信问题。下文都是基于簇头和SN间的上行系统来研究。
K个节点在相同的时间-频率资源下发送数据(M≥K+1),则簇头接收的信号为:
y=P1/2Gx+n
(3)

G可表示为:
G=HD1/2
(4)
其中,H是簇头和K个节点间的M×K的快衰落系数矩阵;D=diag{β1,…,βk,…,βK},βk表示节点k的大尺度衰落因子。
文中采用ZF检测得:
r=AHy=P1/2AHGx+AHn
(5)
其中,A为ZF检测矩阵;rk和xk分别是矩阵r和x的第k个元素,则
其中,ak和gk分别是矩阵A和G的第k列。
式(6)中3项分别是节点k的期望信号、其他用户的干扰和噪声。并假设信道是遍历的,则节点k遍历的上行速率为:
假设簇头端完全已知G,则检测矩阵A=G(GHG)-1,式(7)变换为:
Rk=
(8)
根据Jensen不等式可得其下界为:
log2(1+βkpk(M-K))
(9)
如图2所示,理论值和吞吐量下界值分别是式(7)和式(9)的求和结果,可看出推导的吞吐量下界值与理论值非常接近。因此,1.2节中的系统吞吐量用下界值来代替理论值。

图2 系统的吞吐量比较(K=10)
1.2 基于能效下界的最优化模型
根据1.1节中的吞吐量下界的推导,则系统总吞吐量的下界为:
(10)
系统的总功率消耗包括所有节点发射功率和簇头端固定电路消耗两部分,表示为:
其中,PC是每根天线固定电路功率消耗,包括A/D转换、接收滤波器、混频器、低噪声放大器等。系统的能效下界函数可表示为:
除考虑能效以外,在实际CRAHNs网络中,不同设备的最大功率和数据速率要求都不同,因此文中还考虑了节点的最大发射功率限制以及QoS要求。基于以上分析,可得到多节点MassiveMIMO上行系统中能效资源分配的约束最优化问题,即:
(13)

2 多节点Massive MIMO上行系统中能效资源分配算法
上述能效下界函数是分数形式且非凸,因此可采用文献[14]中分数规划的性质将其转化为减数形式,式(12)可转化为:
其中:

(14)
因此,式(13)中的约束最优化问题可转化为:
(15)
假设
则函数f的Hesse矩阵为:
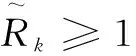
其中,λk≥0和μk≥0分别对应式(15)中两个约束条件的Lagrangian乘子。因此,式(15)的对偶问题可表示为
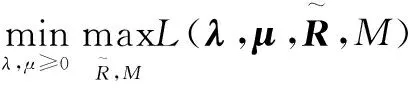
给定λ和μ,各节点的最优发射速率和簇头天线数为:
(16)

(17)

Lagrangian乘子迭代式如下:
(18)
(19)
其中,[x]+=max{0,x};i表示迭代次数;ε表示迭代步长。
其中,α为常数,用来调整收敛速度。
用Dinkelbach迭代方法[14]求解最优化问题,具体迭代资源分配算法如下:
(2)设置迭代次数n=0,q*=0;
(6)Endwhile
3 仿真结果与分析
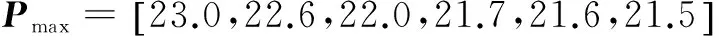

图3 不同节点数的能效以及天线数比较
从中可看出:
(1)随着节点数的增加,系统的能效性能明显提高,因为节点数的增加可使系统的节点分集特性更为明显。并且文中算法接近穷举算法的能效性能。
(2)因为节点最低速率要求及最大功率限制,使得有约束条件时系统能效相较于无约束时有所降低。
图3的下图是与上图相同设置时的天线数比较。从中可以看出,随着用户数的增加,BS端所配置天线数明显增加,与式(17)相吻合。有约束比无约束时天线数有很大增加,这是因为在节点的最大功率Pmax较小时,又要保证一定的最小速率Rmin,只能靠增加簇头端天线数来降低节点发射功率、提高发射速率。
图4给出了不同节点时两种情况下系统的频谱效率。

图4 不同节点数时的频谱效率比较
从图4中可以看出,随着节点数的增加,系统的频谱效率显著提高。图4是保证最小速率Rmin为1 bit/(s·Hz)时,设置不同Pmax的结果,此时两种情况下簇头天线数近似,但是明显有约束比无约束时的频率效率要小,这是因为Pmax值的约束设置得较小。
图5给出了文中迭代算法在节点数为15、不同发射功率Pmax下各迭代次数的能效比较。

图5 不同最大发射功率时各迭代次数的能效比较(K=15)
从图5中可看出,最大功率越大,系统的能效越大,但当最大功率达到一定值时,并不影响最大能效值。此外,在迭代次数为5时,即达到最大能效的95%,可在迭代次数10内得到能效最大值。
图6的上图给出了在最小速率设置为1 bit/(s·Hz)时,无约束和有约束时节点1~5的频谱效率比较。从中可以看出,无约束时节点1~5的频谱效率相同,这是因为没有最大功率的限制,这时节点所消耗功率也相同。而有约束时节点1~5因最大功率的不同而不同,并且最大功率越大,相应的频谱效率也越大,节点的功率消耗如图6的下图所示。
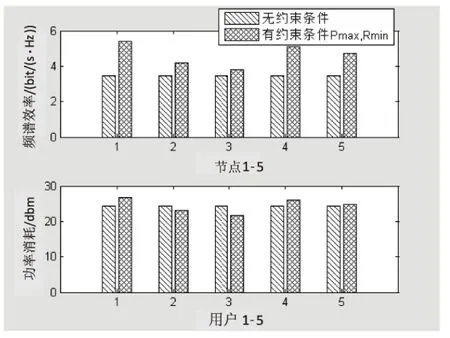
图6 节点1~5在两种情况下的频谱效率和功率消耗对比(β=1,Pmax=[0.5,0.2,0.15,0.4,0.3] W)
表1是相同最大功率和最小速率限制下,不同的大尺度衰落因子β时的节点速率和功率消耗。

表1 不同β时的节点速率和功率消耗
从表1中可以看出,β越大,功率消耗以及速率都越大。这是因为信道条件好的节点会被分配更多的资源。
4 结束语
文中在CRAHNs网络中,研究了基于MassiveMIMO上行系统的能效资源分配算法。在簇头端完全已知CSI时,采用ZF检测,建立了最大能效下界的非凸优化模型。因为在CRAHNs网络,各移动设备的最大功率和最小数据功率不同,因此增加了约束条件。根据分数规划的性质,将能效函数分数形式转化为减式形式,利用凸优化求解获得最大能效。理论分析和仿真结果表明,所提算法在能效上近似最优值,满足节点的最小数据速率及其最大功率限制,且能以较小的迭代次数收敛到最优能效性能。
[1]AkyildizIF,LeeWon-Yeol,ChowdhuryKR.CRAHNs:cognitiveradioadhocnetworks[M].[s.l.]:ElsevierPublishingHouse,2009:810-836.
[2]KumarR,GurugubelliJ.HowgreentheLTEtechnologycanbe?[C]//Procof2ndinternationalconferenceonwirelesscommunication,vehiculartechnology,informationtheoryandaerospace&electronicsystemstechnology.[s.l.]:[s.n.],2011.
[3]ZhouXingyu,BaiBo,ChenWei.AntennaselectioninenergyefficientMIMOsystems:asurvey[J].ChinaCommunications,2015,12(9):162-173.
[4]LarssonEG,TufvessonF,EdforsO,etal.MassiveMIMOfornextgenerationwirelesssystems[J].IEEECommunicationMagazine,2014,52(2):186-195.
[5]NgoHQ,LarssonEG,MarzettaTL.EnergyandspectralefficiencyofverylargemultiuserMIMOsystems[J].IEEETransactionsonCommunications,2013,61(4):1436-1449.
[6]KhansefidA,MinnH.AsymptoticallyoptimalpowerallocationformassiveMIMOuplink[C]//Procof2014IEEEglobalconferenceonsignalandinformationprocessing.[s.l.]:IEEE,2014.
[7]NgDWK,LoES,SchoberR.Energy-efficientresourceallocationinOFDMAsystemswithlargenumbersofbasestationantennas[J].IEEETransactionsonWirelessCommunications,2012,11(9):3292-3304.
[8]MiaoGuowang,HimayatN,LiGY.Energy-efficientlinkadaptationinfrequency-selectivechannels[J].IEEETransactionsonCommunications,2010,58(2):545-554.
[9]DaiLinglong,WangZhaocheng,YangZhixing.Spectrallyefficienttime-frequencytrainingOFDMformobilelarge-scaleMIMOsystem[J].IEEEJournalonSelectedAreasinCommunications,2013,31(2):251-263.
[10]FuLiqun,ZhangJ,HuangJianwei.EnergyefficienttransmissionsinMIMOcognitiveradionetworks[J].IEEEJournalonSelectedAreasinCommunications,2013,31(11):2420-2431.
[11]CuiShuguang,GoldsmithAJ,BahaiA.Energy-efficiencyofMIMOandcooperativeMIMOtechniquesinsensornetworks[J].IEEEJournalonSelectedAreasinCommunications,2004,22(6):1089-1098.
[12]RusekF,PerssonD,LauBK,etal.ScalingupMIMO:opportunitiesandchallengeswithverylargearrays[J].IEEESignalProcessingMagazine,2013,30(1):40-60.
[13]LeNP,TranLC,SafaeiF.Adaptiveantennaselectionforenergy-efficientMIMO-OFDMwirelesssystems[C]//Procof17thinternationalsymposiumonwirelesspersonalmultimediacommunications.[s.l.]:[s.n.],2014.
[14]DinkelbachW.Onnonlinearfractionalprogramming[J].ManagementScience,1967,13:492-498.
Energy-efficient Resource Allocation for Massive MIMO Uplink Systems
JIANG Ai-zhen,ZENG Gui-gen
(Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
An energy-efficient resource allocation algorithm for Massive MIMO uplink system in Cognitive Radio Ad Hoc Networks (CRAHNs) is studied.In the case of a Zero-Forcing (ZF) receiver in cluster,the considered problem is modeled as a non-convex optimization based on energy-efficient lower bound.Furthermore,the optimization takes into account the circuit power consumption,minimum required data rate and maximum required power of each node.According to the properties of fractional programming,the resulting energy-efficient optimization in the fractional form is transformed into subtractive form.Convex optimization is exploited to obtain the numbers of antennas and optimal transmit power of each node which lead to maximum energy efficiency.Simulation shows that the proposed algorithm approximates the optimal value of the energy efficiency,satisfies the minimum data rate and the maximum power constraint,and converges to energy-efficient optimization in a small number of iterations.
Massive MIMO;energy efficiency;resource allocation;uplink systems;fractional programming;CRAHNs
2015-12-22
2016-04-20
时间:2016-09-19
国家自然科学基金面上项目(61471202)
江爱珍(1990-),女,硕士研究生,研究方向为大规模MIMO资源分配和信道估计;曾桂根,副教授,硕士生导师,研究方向为MIMO通信信号处理、协作通信、绿色通信等。
http://www.cnki.net/kcms/detail/61.1450.TP.20160919.0839.014.html
TP301.6
A
1673-629X(2016)10-0200-05
10.3969/j.issn.1673-629X.2016.10.044

