一种Douglas-Peucker与Li-Openshaw结合改进的曲线化简方法

顾 腾, 陈晓勇， 刘成强

(1.东华理工大学 测绘工程学院，江西 南昌 330013；2.中南大学 地球科学与信息物理学院，湖南 长沙 410083)

一种Douglas-Peucker与Li-Openshaw结合改进的曲线化简方法

顾 腾1, 陈晓勇1， 刘成强2

(1.东华理工大学 测绘工程学院，江西 南昌 330013；2.中南大学 地球科学与信息物理学院，湖南 长沙 410083)

Douglas-Pecuker算法能够很好的保证对线的特征弯曲点保留和对点其它非特征点的压缩，但化简出来的结果过于生硬且在特征点处产生尖角，不能够在地图综合中普遍使用。Li-Openshaw算法能很好地圆滑线的尖角且不会显得过于生硬，但也会对线的特征点圆滑。提出了将两者结合的改进型算法，做到特征点保留且做到在其它处化简。并将该改进型算法与另外两种算法进行实验验证对比。实验结果表明，两者结合的改进型算法展现出了两者的优点，且能够在自动制图中得到应用，优化地理线要素和面要素的化简。

Douglas-Peucker；Li-Openshaw；线化简

地图由以前的多年更新一次到现在的一年一次，甚至半年一次。这对制图工作者带来巨大的工作量，迫切需要一种能够代替人机交互制图的软件。在地图综合中线要素占了很高的比例，比如道路、河流这些也是极其重要的地理要素。对于这类线要素的化简已经有Douglas-Peucker (Douglas et al., 1973)、Li-Openshaw( Li et al.,1994)、弦比弧算法(Nako et al.,2003)，每种算法都有自身的优缺点，比如：Douglas-Peucker算法能够很好的保留曲线特征，但缺点是不能对曲线做到很好的自然概括；Li-Openshaw算法可以对曲线进行自然融合概括但缺点也对曲线特征进行概括；弧比弦算法具有对曲线弯曲处概括的优点，但可能产生连续的节点剔除 而使局部曲线形状有较大的变形。如何做到能够在实际制图中得到应用这才是最重要的。

1 Douglas-Peucker和Li-Openshaw的结合

1.1 Douglas-Peucker算法(简称D-P算法)

D-P算法主要是对曲线上的点进行压缩，并且保留线的主要特征。该类算法在很对线的压缩中应用广泛，其原理简单，效率高且不会产生多余的点，这是一类较早出现的算法，亦是一类非常经典的算法，目前很多算法在结果对比的时候都会与之做比照。

D-P算法原理如图1a，先将折线ABCDEFG两端AG连接成一条线。首先计算出折线上到线AG的垂直距离d最大的点C；如果d < threshold，则将线段AG作为该折线近似。如果d > threshold，则用点B将该折线分为CA，CG两个部分；继续重复以上步骤。最后依次连接各个分割点形成的折线，即可以作为原折线的近似。ACEG为原折线化简后的折线。如图对比使用D-P算法化简前后的线段。

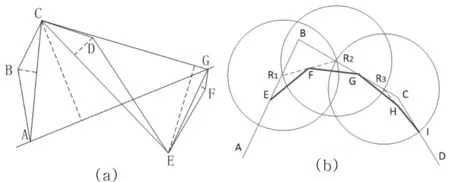
图1 Douglas-Peucker与Li-Openshaw算法Fig.1 Dougals-Peucker and Li-Openshaw algorithma.Douglas-Peucker算法；b.Li-Openshaw算法图

1.2 Li-Openshaw算法(简称L-D算法)

L-O算法的基本思想：

(1)按照目标比例尺和原比例尺来估算出圆形SVO的尺寸R。

(1)

其中St为需要化简后的目标比例尺，Sf为原比例尺。D是一个参数，为化简后地图上的SVO的参数。Muller则认为在地图上D取0.4mm为能保证视觉分辨的最小值。

(2)如图1b所示，首先确定圆形SVO的起始位置，一般设为第一端点A，当在R1处，以R1为圆心，R为半径画圆与原折线交于R2处。

(3)选择R1R2连线的中点F为综合后的选取点。

(4)从R2点开始重复2、3步骤，直到末端点D不在SVO圆内结束。

在图1b中，折线ABCD为原化简前线段，AEFGHID为综合化简后的结果。

1.3 Douglas-Peucker与Li-Openshaw结合改进型算法

基于以上的分析可以发现，单独应用D-P算法会使线要素化简结果粗糙、僵硬，单独应用L-O算法则会出现保留点混乱、曲线整体形状变形等情况，基于线化简的目的，以尽量保持线要素特征点、保证线要素形状特征、线要素化简结果圆滑美观为原则，本文提出一种Douglas-Peucker与Li-Openshaw结合的简单曲线化简方法，对线化简算法进行改进。其基本原理如图2：

图2 D-P与L-O结合改进算法Fig.2 Combined Douglas-Peuceker with Li-Openshaw improved algorithm

(1)对进行综合化简的曲线采用D-P算法计算出折线上的满足垂直距离大于距离阈值的拐点，如图2所示，B，C，D，F为满足条件的拐点。

(2)使用L-O算法从起点A为圆心，R为半径的圆形SVO对该折线进行化简。对于拐点聚集处(如图2中拐点B处)，以B点为圆心，画一个半径为R1(R1=R)的圆O，如果B点前后有拐点(C、D)在圆O范围内，则记录C，D，视情况对C，D两点进行处理。如果需要处理C，D两点，则以B点为圆心，更改SVO半径(如1/2 R)重新画圆对C，D圆滑概括；如果不需要则不做圆滑处理。对于拐点稀疏处(如图2中拐点F处)，处理如下：以F点为圆心，画一个半径为R1(R1=R)的圆O进行圆滑处理。

顺序处理直至到达末端的I结束。图2中，ABCEFI为原曲线，ABCDEGHI为化简后曲线。

2 实验及分析

2.1 改进算法结果

由于本文是借鉴NewMap软件底层平台，采用C++语言编程进行算法实现。本文算法是Douglas-Peucker与Li-OpenShaw结合改进算法，因此综合化简之后与这两种算法进行比较分析。本文采用了这三种算法在参数一定(1∶1万到1∶10万化简)的情况下，对南方某城市地图1：1万道路与水系数据综合化简(图3、4)。

按照本次算法的综合化简思路，综合化简后的结果应该加贴切原始曲线相比另外两种算法，从目视上看，结果与原思路结果一致。图3a中，D-P算法在对道路化简时保留住原始特征点，而且对线要素也做到了一个很好的压缩，但是在制图综合中适用性不是很强，很多情况下需要对地理线要素做圆滑处理；图3b道路线是采用L-O算法化简前后的对比图，从图中可以看出L-O算法在综合化简中对道路线做到了圆滑过滤，但在现实制图综合中不光要求圆滑，还要求保留原有的特征弯曲不作处理或者是细微处理；图3c采用本文介绍的两者结合改进算法对道路线综合前后的对比图，从图中可以明显看出其综合化简后的结构由于前两者的化简结果，不仅在对道路线要素化简中做到了圆滑，而且还能够保留原有的特征弯曲，这极大的增加了该算法在制图综合过程中适用性。

图4是对南方某城市1∶1万水系数据化简结果，比较这三种算法对水系化简结果，再次验证了本文算法的结合了两种经典化简算法的优点，在大弯曲的地方进行了特征保留。

实线是原始地图数据，虚线是化简后的结果。

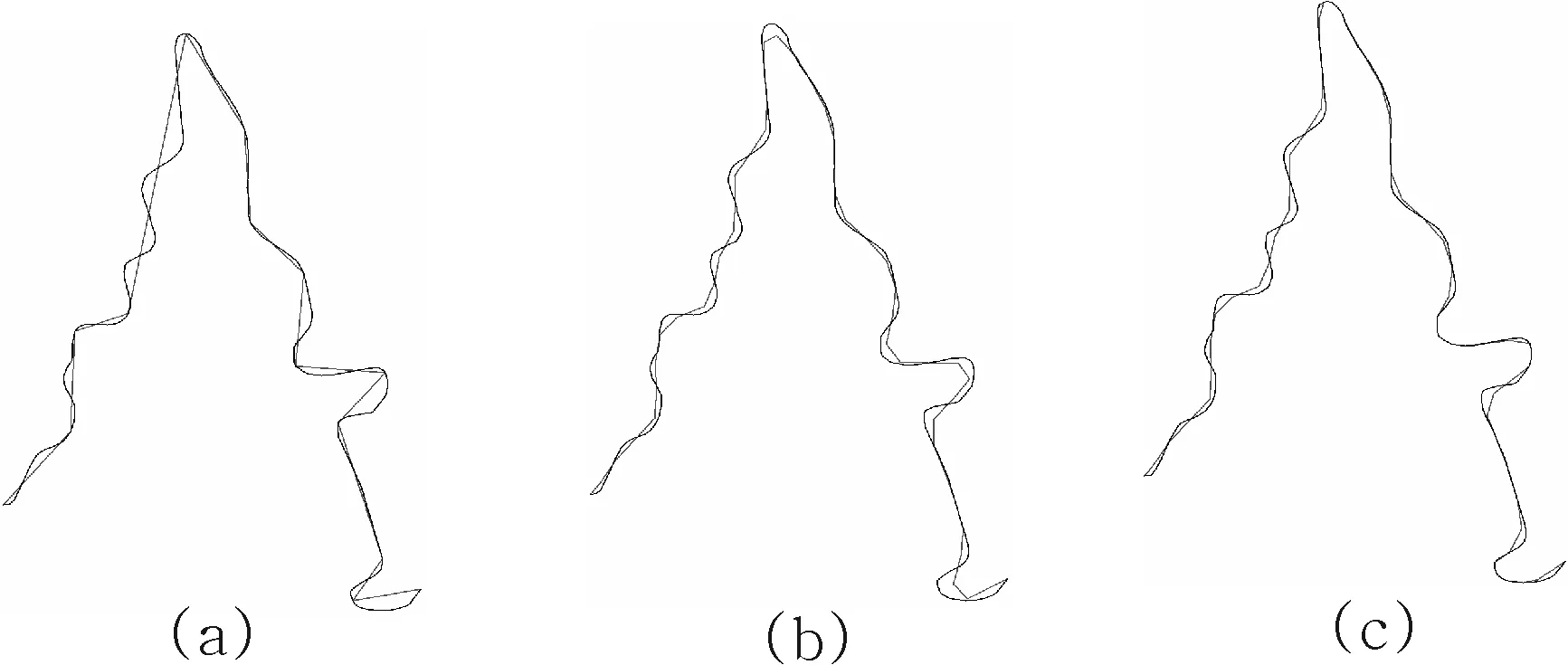
图3 三种算法对1∶1万道路要素化简结果对比Fig.3 A comparison of three algorithms for 1∶1 million scale road simplification resultsa.Douglas-Peucker算法；b.Li-OpenShaw算法； c.本文改进算法

图4 三种算法对1∶1万水系要素化简结果对比Fig.4 A comparison of three algorithms for 1∶1 million scale river simplification resultsa.Douglas-Peucker算法;b.Li-Openshaw算法;c.本文改进算法

2.2 结果分析

由White提出的地理线要素化简的两个评价指标：矢量位移，面积位移(White，1985)。化简后的曲线与原始曲线之间对应点位位置偏差称之为矢量位移。面积位移则指的是化简后的新曲线与原始曲线之间所围成部分的面积(刘慧敏等,2011;邓敏等,2009)。如图5所示显而易见，算法化简结果的优良取决于面积位移和矢量位移，本文采以上两个定量指标进行评价。

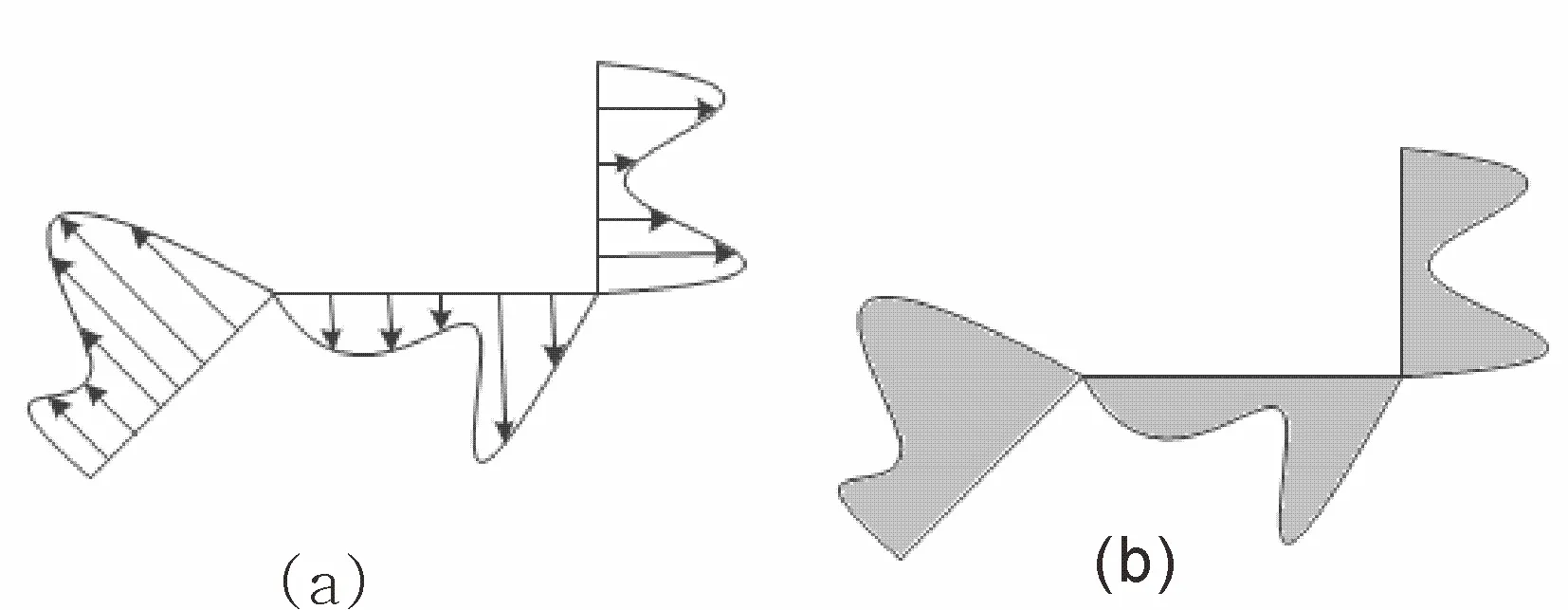
图5 评价指标Fig.5 The parameters for the evaluationa.矢量位移;b.面积位移

分别对三种算法对道路线和水系线做综合化简后的结果进行指标评价，做简单的比较可以发现改进后的算法不光在直接的视觉感官上看效果优于其它两种算法，而且从其中两项评价指标也能看出结果也是优于其它两种算法。从整体指标来看，本文改进型算法在参数一定(1∶1万至1∶10万)，化简各项指标下都优于其它两种算法，展现出D-P与L-O算法的优点。

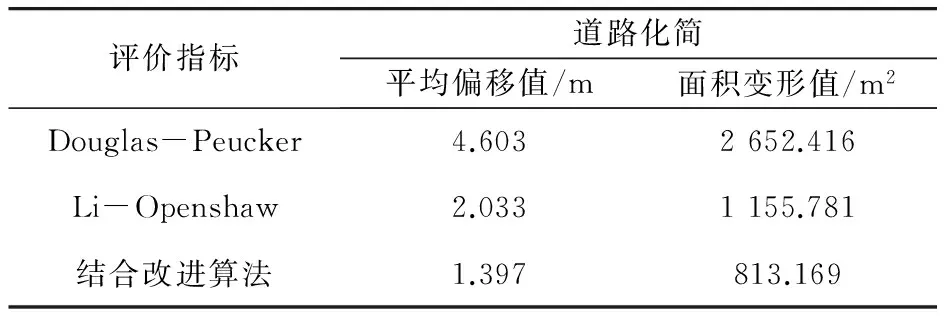
表1 道路矢量位移与面积位移评价结果

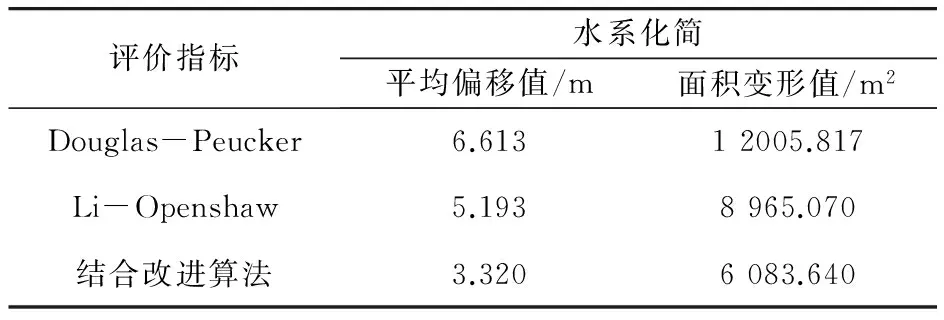
表2 水系矢量位移与面积位移评价结果

由Muller提出的关于评价位移指标的位移标准差(Muller,1987)，该评价指标适用于不同方法对同一线要素化简的结果评价(Joao E M, 1998; 朱鲲鹏等，2007；武芳等，2008)。具体计算方法：

SMD(%)100(1-(S-D)/S)

(2)

式中的S为算法化简后，在原始曲线上位移最大的点到原始曲线首末端点连线的距离，D为该点化简前后的位移值。

当然此处只用位移标准差来单独评价是不够，通过分析位移标准差时发现，该评价指标值对局部最大值进行了评价，因此评价不够精确。进一步采用位移位置误差来评价化简前后的整体位移，使用化简前后曲线相交围成的面积与原曲线长度的比值。具体计算方法：

(3)

式中，ΔS表示曲线化简前后相交围成的面积；L表示原始曲线的长度。

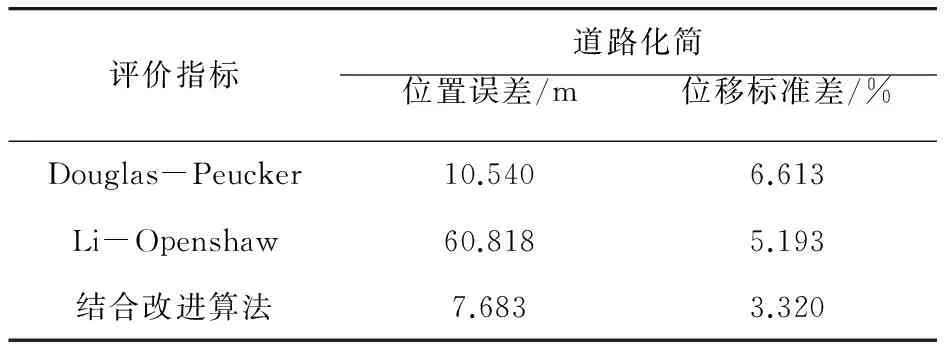
表3 道路位移标准差与位置误差评价结果

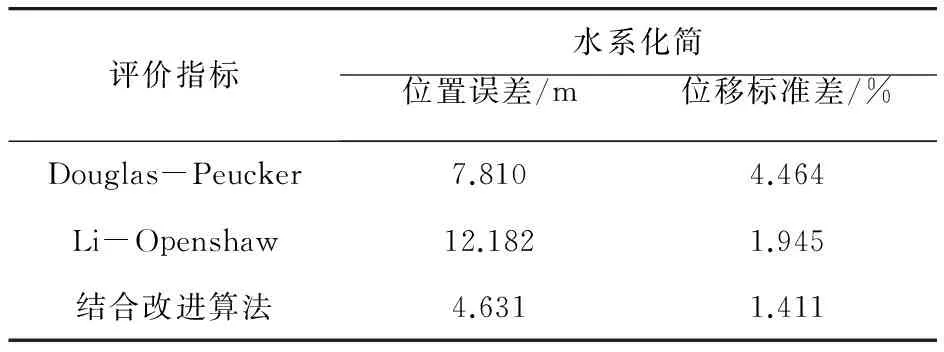
表4 水系位移标准差与位置误差评价结果

对比以上两种评价指标，改进后的算法都展现出良好的性能。

4 结论与展望

本文在制图综合这样一个大背景下，结合实际要求，对地理线要素化简算法研究。发现现有算法的在对线要素化简实际应用受限。提出了Douglas-Peucker与Li-Openshaw两者结合改进的算法；该方法既能够在曲线特征保留，又能对其他非特征化简；并通过实验并采用4种不同的定量指标进行评价，结果表明本文提出的改进算法在1∶1万至1∶10万化简结果的正确性和有效性。但还需要更深一步的研究内容有：考虑综合前后比例尺跨度太大情况下的一种自适应算法；考虑地理面要素，提出能针对面要素的一种能够自适应化简算法。

邓敏,陈杰,李志林,等.2009.线目标化简中节点重要性度量方法比较及垂比弦法的改进[J].地理与地理信息科学,25(1):40-43.

刘慧敏,樊子德,徐震,等.2011.曲线化简的弧比弦算法改进极其评价[J],地理与地理信息科学,27(1),45-48.

武芳,朱鲲鹏.2008.线要素化简算法几何精度评估[J],武大学报：信息科学版,33(6):600-603.

朱鲲鹏,武芳,王辉连,等.2007.Li-Openshaw算法的改进与评价[J],测绘学报,36(4):450-456.

Douglas D H，Peucker T K. 1973. Algorithms for the reduction of the number of points required to represent a digitized line or caricature[J].Canadian Cartographer,10(2);112 -122.

Joao E M.1998. Causes and Consequences of Map Generalization[M].London: Taylor and Francis.

Li Z L,Openshaw.1994.基于客观自然规律的线状要素自动综合的算法[J].武大译文,(1)：49-58.

Muller J C.1987. Fractal and Automated Line Generalization[J].The Cartographic Journal,24(1):27-34.

Nako B,Mitropoulos V.2003. Local length ratio as a measure of critical point detection for line simplification[A].The Symposium of the 5th ICA Workshop on Progress in Automated Map Generalization.28-30.

White E.1985. Assessment of line generalization algorithms using characteristics points [J].The American Cartographer,12(1):17-27.

A modified Line Simplification Method Combined Douglas-Peucker with Li-Openshaw

GU Teng1, CHEN Xiao-yong1, LIU Cheng-qiang2

(1.School of Geomatics，East China University of Tecnology,Nanchang，JX 330013，China；2.School of Geosciences and info-Physics，Central South University，Changsha,HN 410083，China)

There are two classic line simplification algorithm:Douglas-Peucker and Li-Openshaw.Douglas-Peucker algorithm can remain bending feature points and compress other non-feature points. But the Simplification result too stiff and produces sharp in the feature point.So It can’t be widely used in map generalization.Li-Openshaw algorithm can smooth sharp line and does not seem too stiff,but will also feature a dotted line of sleek. How to combine the two algorithms and to show the advantages of both.This parper presents a modified line simplification algorithm combined the two algorithms.This method can reserve feature points and simplify others.There is a modified algorithm and two other algorithms comparative experiment in this pearper.

Douglas-Peucker；Li-Openshaw；Line Simplify

2016-09-17

测绘地理信息公益性行业科研专项(201512020，201512027 )

顾 腾(1993—)，男，硕士，主要从事地图制图与综合研究。E-mail:tengku08@163.com

10.3969/j.issn.1674-3504.2016.04.015

O29

A

1674-3504(2016)04-0396-05

顾腾,陈晓勇，刘成强.2016. 一种Douglas-Peucker与Li-Openshaw结合改进的曲线化简方法 [J].东华理工大学学报：自然科学版，39(4)：396-400.

Gu Teng,Chen Xiao-yong,Liu Cheng-qiang.2016. A modified line simplification method combined Douglas-Peucker with Li-Openshaw [J].Journal of East China University of Technology (Natural Science), 39(4)：396-400.