漳州盆地深部岩层温度数值模拟及热储量估算
刘唐伟, 孙占学, 王安东, 胡宝群, 刘金辉
(1.东华理工大学理学院,江西 南昌 330013; 2.东华理工大学核资源与环境教育部重点实验室, 江西 南昌 330013 )
漳州盆地深部岩层温度数值模拟及热储量估算
刘唐伟1, 孙占学2, 王安东2, 胡宝群2, 刘金辉2
(1.东华理工大学理学院,江西 南昌 330013; 2.东华理工大学核资源与环境教育部重点实验室, 江西 南昌 330013 )
分别采用一维和二维热传导数学模型,对漳州盆地典型区域深部温度进行了数值模拟,并进行了热储量的初步估算。首先由实测样品数据得到地表生热率和热导率等参数,再由所得地表生热率计算深部生热率,依据地球物理勘探解释结果,给出地层结构和厚度等参数。然后分别利用一维分层热传导模型和二维稳态热传导模型进行数值模拟,得到不同条件下5 000 m以浅不同深度的温度值。最后基于数值模拟参数,给出了研究区分层热储量的计算结果。
漳州盆地; 生热率; 温度场数值模拟; 热储量
盆地深部地温场数值模拟及干热岩热储量估算是一个具有重要理论意义与应用价值的课题。 近年,很多学者对中国大陆不同地区干热岩地热资源潜力进行评估,取得了一定成果(汪集旸等,2012;蔺文静等,2012;徐立等,2014;万建军等,2015)。地热田干热岩所蕴含的地热资源量取决于干热岩的温度及干热岩岩石的热物性。根据已有研究,干热岩资源的估算至少需要如下数据:大地热流值、岩石热导率、岩石生热率、放射性元素集中层的厚度等。其中深部岩层温度一般不能直接测出,通常采用数值模拟的方法得到(汪集旸等,2012;庞忠和等,2014)。本文拟对漳州盆地部分区域深部温度采用不同方法进行数值模拟计算,并进行简要分析对比,进一步采用体积法计算热储量。低孔渗岩石介质中热储量的体积法计算公式如下:
Q=ρCPV(T-T0)=ρCPSh(T-T0)
(1)
式中,Q表示干热岩资源热储量;ρ表示岩石密度;Cp表示岩石比热容;S表示岩体或热储层面积;h表示岩体或热储层厚度;T表示要计算特定深度的岩体温度;T0表示地表平均温度(汪集旸等,2012;蔺文静等,2012;徐立等,2014)。
地表温度是特定深度温度计算的必要参数,可通过计算年平均气温来近似替代地表温度。漳州盆地地表参考温度可取值为25 ℃。盆地深部温度计算时需要依据地表和钻孔等实测数据,分区域和岩石类型对参数进行合理取值,才能获得与实际一致的结果(王安东等,2015)。目前该盆地钻孔深度一般小于5 000m,由于岩石样品的不足,不同区域地下深部温度一般不能够直接测量得到,本文采用几种不同方法估算不同区域特定深度下的生热率和温度。
关于漳州盆地地壳结构的认识,主要来源于已有研究工作——漳州盆地某测线的综合解释(朱金芳等, 2006),见图1。

图1 漳州盆地及其邻区地壳结构综合解释图(据朱金芳等,2006)Fig.1 Crust structure integrated interpretation chart of Zhangzhou basin and its adjacent regions (According to Jin-fang Zhu, etc., 2006)
1 一维分层模型数值模拟
据已有研究可知,沉积岩的深部温度计算公式为
T(z)=T0+q0z/K-Az2/2K
(2)
变质岩、火成岩深部生热率计算用公式
A(z)=A0exp(-z/D)
(3)
式中T为深部温度,z为深度,T0为地表平均温度或特定参考温度,q0为地表热流,K为岩石热导率,A为岩石生热率,D为放射性生热元素富集层的厚度,A0为地表生热率。地幔热流无法直接测得,可用多种方法推算,大体是区域地表热流的60%,大致与“剩余热流”相等。对于漳州地区地幔生热率,已有研究给出岩石生热率为0.024μW/m3(赵平,1993)。放射性生热元素富集层的厚度一般取值为10 000m左右。我国大陆由于受到中生代-新生代构造作用的强烈改造,导致东部晚中生代的伸展作用,使得地壳拉张减薄,西部岩石圈显著增厚和青藏高原隆升。这些构造作用必然影响放射性元素富集层的厚度,所以在研究中根据地区特征来选取放射性元素的富集层的厚度。按照漳州盆地地球物理勘探研究结果,漳州盆地D值约在10 000~12 000m。地表温度是特定深度温度计算的必要参数,可通过计算年平均气温来近似替代地表温度(表1)。
首先按照公式(2)进行深部温度计算,得到4 000m深部温度为99.67 ℃。深部岩石生热率用
深部热导率公式计算,以1 000m深度为分层计算单元节点,用温度公式递推计算深部温度,如分别取q0=75 mW/m2和q0=85 mW/m2,得到深部岩层温度计算结果T1和T2(表2)。
2 二维稳态热传导方程数值模拟
2.1 数值模拟1
首先考虑二维稳态热传导方程。研究区域为深90 000 m,宽180 000 m的二维矩形区域。取地表作为温度场顶界面,地表平均温度取为25 ℃,以温度值为1 330 ℃的等温面作为热岩石圈底界面,两边边界取为绝热边界。考虑地表生热率取实测均值3.0 μW/m3。上地壳12 000 m生热率按前述公式(3)计算,D取为10 000 m,下地壳用地震波速度估计,地幔生热率取为0.024 μW/m3。地壳热导率取地表实测均值3.0 W/(m·K),地幔热导率取为2.5W/(m·K)。二维模拟计算参数如表3。

表1 一维模拟计算参数

表2 一维模拟计算结果
对宽度和深度进行无维化转换后(0~180 000 m转换为-1~1;0~90 000 m转换为0~-1),基于Matlab 微分方程工具箱,对二维稳态热传导方程用有限元数值方法求解,计算网格与模拟温度分布如图2。
其中,u(512),u(514), u(515),u(517)为3 600 m(y=-0.04)左右深度的温度值,为71℃; u(153),u(154), u(206),u(510)为7 200 m (y=-0.08)左右深度的温度值117 ℃;u(516),u(693), u(693)为10 800 m(y=-0.12)左右深度的温度值,为163 ℃。相对一维模拟结果偏低。如放射性富积层厚度D设为12 000 m,再进行数值求解,所得温度没有太大变化。
然后考虑地表沉积层厚度的影响,设地表沉积层厚度为30 m,生热率取为1.0 μW/m3,热导率取为1.6 W·m-1K-1,所得数值模拟结果为:3 600 m(y=-0.04)左右深度的温度值为76 ℃;7 200 m(y=-0.08)左右深度的温度值为124 ℃;10 800 m(y=-0.12)左右深度的温度值为167 ℃。所得温度比不考虑沉积层厚度的影响要略高。假如地表沉积层厚度为300 m,所得数值求解结果为:3 600 m(y=-0.04)左右深度的温度值为80 ℃左右。

表3 二维模拟计算参数

图2 计算网格节点图a(D=10 000 m) Fig.2 All computing grid nodes (D=10 000 m)
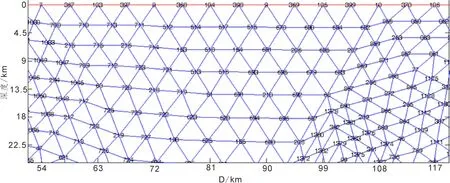
图3 部分计算网格节点图a(D=10 000 m) Fig.3 Part nodes of computing grid a(D=10 000 m)

图4 深部温度模拟计算分布图a(D=10 000 m) Fig.4 Deep temperature simulation map a (D=10 000 m)

图5 局部计算网格节点图b(D=12 000 m) Fig.5 Part nodes of computing grid b(D=12 000 m)
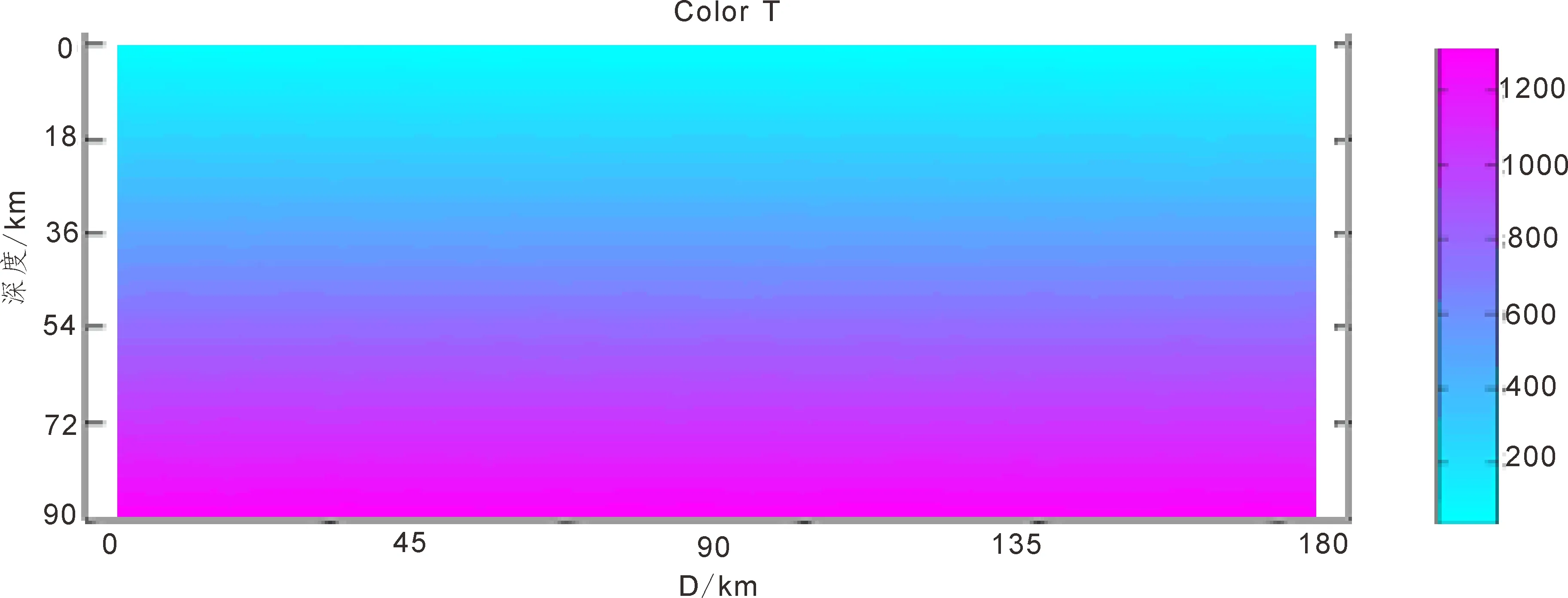
图6 深部温度模拟计算分布图b(D=12 000 m) Fig.6 Deep temperature simulation map b (D=12 000 m)
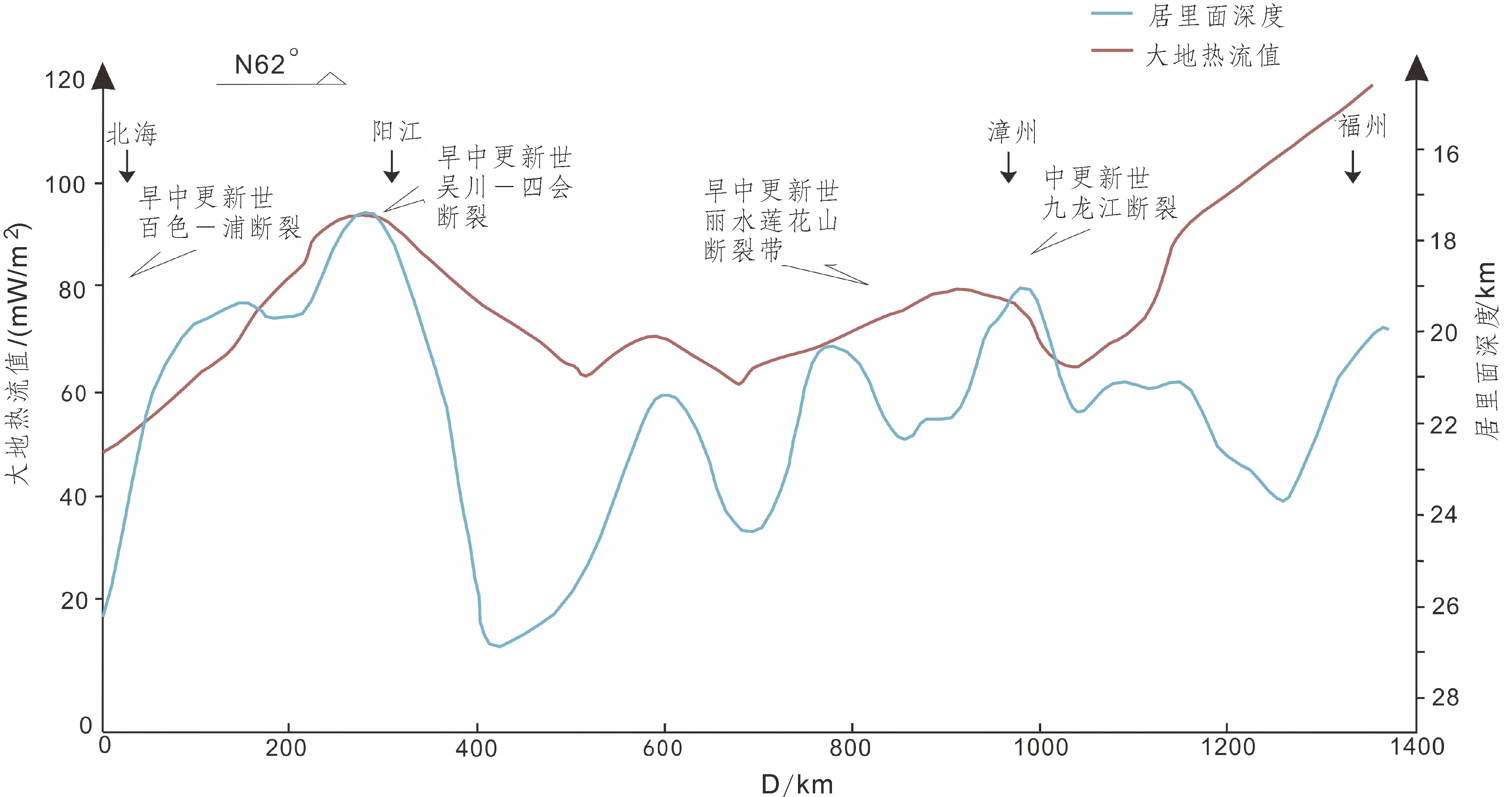
图7 Ⅱ-Ⅱ剖面(1370000 m)(北海-福州)(据王贵玲,2014)Fig.7 Ⅱ-Ⅱ Profile (1370 000 m), (the Beihai-Fuzhou)(According to the Gui-ling Wang, 2014)
2.2 数值模拟2
考虑二维稳态热传导方程,。研究区域为深19 000 m,宽38 000 m的二维矩形区域。取地表作为温度场顶界面,地表平均温度取为25 ℃,以地下19 000 m居里面作为模拟区域底界(粘为振,2008;王贵玲,2014), 设该处温度值为578 ℃(王贵玲,2014),两边竖直边界取为绝热边界。其它计算参数见表3。
对宽度和深度进行无维化转换(0~38 000 m转换为-1~1;0~19 000 m转换为0~ -1),如果忽略地表沉积层影响,数值模拟结果见图8,9。其中,部分节点对应深度的温度值,见表4。
如果考虑地表沉积层等因素影响,设地表沉积层厚度为30 m,生热率取为1.0 μW/m3,热导率取为1.6 W/(m·K),数值模拟结果见图10,11。
计算所得3 820 m处温度大约为150 ℃。部分节点对应深度的温度值见表5。如果设地表沉积层厚度为300 m,3 820 m处温度大约为158 ℃。
漳州盆地某些区域钻井数据显示部分区域3 000 m深度温度值为90~100 ℃,与数值模拟计算结果对比表明,一维模型模拟结果能基本反应不同深度的温度均值;对于二维稳态热传导模型,如果以底部90 000 m处,温度值1 330 ℃的等温面作为热岩石圈底界面的,计算出的深部岩石平均温度相对偏低,可以考虑作为模拟区域温度值的下限,主要原因是计算时对地壳和地幔分层较粗,没有详细区分岩层的不均匀性,也没有考虑外部热源;而用居里面作为底部界面,由于模拟区域相对变小,不确定因素的影响也较少,计算结果会比较准确,但是显然不同区域居里面的温度和深度值较难确定,而居里面的温度和深度变化直接影响到地温场的计算结果,具体区域不同,居里面的温度和深度值不同,所得到的数值模拟结果也会不同,本文以居里面为底界所得数值模拟结果较高,可以考虑作为模拟温度值的上限。

表4 部分节点二维模拟温度值A

表5 二维模拟部分节点温度值B
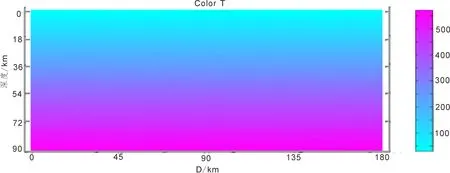
图8 深部温度模拟计算分布图cFig.8 Deep temperature simulation map c
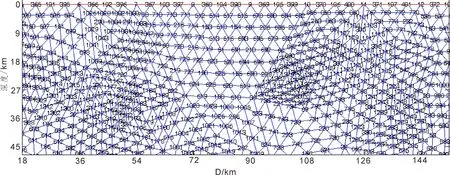
图9 部分计算网格节点图cFig.9 Part nodes of computing grid c

图10 深部温度模拟计算分布图d Fig.10 Deep temperature simulation map d
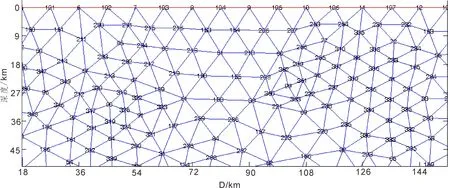
图11 部分计算网格节点图d Fig.11 Part nodes of computing grid d
3 分层热储量估算
下面基于两种不同数值模拟的地温梯度结果,利用公式(1)进行热储量计算,地温场分别参考一维数值模拟结果(表2)和二维数值模拟计算的结果(图8,表4),相应计算所得热储量1和热储量2见表6。
4 结论与展望
本文基于已有研究成果,结合部分区域的部分实测数据, 用不同数值模拟方法,对漳州盆地典型区域地温场进行了初步模拟,在一定假设条件下,得到了不同区域不同深部温度的模拟结果,估算了固定深度温度值的下限与上限。采用不同数值模拟方法计算深部温度的关键一是采用正确的模型与计算方法,二是获得准确的参数值。在今后研究中,可结合研究区域更为详细的数据资料,准确确定模型参数,对模型和方法加以改进,对不同区域深部温度和热储量进行更为详尽的数值模拟计算。

表6 分层热储量计算参数及结果
蔺文静,刘志明,马峰,等.2012.我国陆区干热岩资源潜力估算[J].地球学报,33(5):807-811.
庞忠和,黄少鹏,胡圣标等.2014.中国地热研究的进展与展望(1995-2014)[J].地质科学,49(3):719-727.
庞忠和.1987.漳州盆地地热系统[D].中国科学院地质研究所.
万建军,孙占学,胡宝群,等. 2015.广东佛冈岩体放射性地球化学特征及其干热岩资源潜力研究[J]. 东华理工大学学报:自然科学版, 38(4):398-406.
汪集旸,胡圣标,庞忠和,等.2012.中国大陆干热岩地热资源潜力评估[J]. 科技导报,30(32):25-31.
王安东,孙占学,刘金辉,等. 2015.漳州地区岩石放射性地球化学特征及岩石圈热结构[J].科技导报, 33(24):41-45.
王贵玲.2014. 我国省会级城市浅层地温能调查数据潜力分析[J].供热制冷,(11):64-66.
王贵玲,张发旺,刘志明.2000.国内外地热能开发利用现状及前景分析[J]. 地球学报, 21(2):134-139.
徐立,王良书,杨谦,等.2014.江苏干热岩地热资源潜力估算[J].高校地质学报,20(3):464-469.
粘为振. 2008.漳州地热田成因模式及其与控制构造的关系研究[J].安全与环境工程,15(4):30-33.
赵平.1993.中国东南地区岩石生热率研究[D].中国科学院地质研究所.
朱金芳,方盛明,张先康等.2006.漳州盆地及其邻区地壳深部结构的探测与研究[J].中国地震, 22(4):405-417.
Comparison of Different Numerical Simulation Results of Zhangzhou Basin Deep Rock Stratum Temperature
LIU Tang-wei1, SUN Zhan-xue2, WANG An-dong2, HU Bao-qun2, LIU Jin-hui2
(1.School of Science, East China University of Technology, Nanchang, Jiangxi Province, 330013, P.R.China 2.Fundamental Science on Radioactive Geology and Exploration Technology Laboratory, East China University of Technology, Nanchang, Jiangxi Province, 330013, P.R.China)
This paper simulates the deep rock stratum temperature of the typical area in Zhangzhou basin by numerical method of one-dimensional and two-dimensional heat transfer mathematical model. And the heat storage capacity is preliminary estimated. First the parameters such as thermal conductivity, heat production rate of the surface are obtained by the measured sample data. And the heat production rates of deep area are computed by the heat product rate on surface of the area. According to the results of geophysical interpretation, formation parameters such as structure and thickness of the formation are given. Then some numerical simulation results of temperature value are obtained in different depth of the shallow above 5000 meters under different conditions by using one-dimensional layered heat conduction model and the two-dimensional steady-state heat transfer model, respectively. The layered heat storage capacity are estimated in the typical area based on the parameters by numerical simulation.
Zhangzhou Basin; the Heat Production Rate; Numerical Simulation of Temperature Field; the Heat Storage Capacity
2016-08-04
国家自然科学基金(11561003);江西省教育厅科技计划项目(GJJ150590)
刘唐伟(1973—),男,湖南娄底,博士,副教授,从事优化算法与数值模拟研究。E-mail:twliu@ecit.cn
10.3969/j.issn.1674-3504.2016.04.002
P314.2;O29
A
1674-3504(2016)04-0310-09
刘唐伟,孙占学,王安东,等.2016. 漳州盆地深部岩层温度数值模拟及热储量估算[J].东华理工大学学报:自然科学版,39(4):310-318.
Liu Tang-wei, Sun Zhan-xue, Wang An-dong,et al.2016. Comparison of different numerical simulation results of Zhangzhou basin deep rock stratum temperature[J].Journal of East China University of Technology (Natural Science), 39(4):310-318.

