常幅循环荷载下钢筋混凝土受弯构件疲劳方程研究
刘磊
(华杰工程咨询有限公司,北京100029)
常幅循环荷载下钢筋混凝土受弯构件疲劳方程研究
刘磊
(华杰工程咨询有限公司,北京100029)
国内外对素混凝土及钢材单一材料的疲劳方程已经进行了大量研究并取得了比较成熟的研究成果,但由于钢筋混凝土之间的共同作用,钢筋混凝土构件层面的疲劳方程研究成果尚不多见。论文基于两种材料的疲劳方程,结合钢筋混凝土受弯构件截面基本力学原理,从理论上探讨了钢筋混凝土梁构件层面的疲劳方程,并与已有试验数据进行了对比。
常幅应力;疲劳方程;钢筋混凝土;受弯构件
【DOI】10.13616/j.cnki.gcjsysj.2016.06.006
1 引言
疲劳方程指混凝土(钢材)疲劳强度(应力幅)与极限循环次数之间的曲线方程,反映了材料应力水平与疲劳极限循环次数之间的关系。由于钢筋混凝土构件复合材料的复杂性及钢筋混凝土之间共同作用的相互影响,建立钢筋混凝土构件的疲劳方程成为研究钢筋混凝土构件疲劳性能及寿命预测的难点和瓶颈,迄今为止,对钢筋混凝土构件疲劳方程的研究仍十分有限。
2 混凝土及钢筋材料的疲劳方程
VanO.J.L最早于1907年开始了对素混凝土的疲劳性能,Graf和Brenne研究发现,疲劳起强度不仅取决于循环中的最大应力,也取决于最小应力,确立了经典混凝土应力水平S与极限循环次数N之间的关系曲线[1]:

式中,Smax为循环最大应力水平;N为极限循环次数;R为最大最小应力比;α,β为参数。
式(1)成为素混凝土材料疲劳方程的经典方程,此后Jacobson[2]、浙江省设计院[3]、美国波特兰水泥协会[4]等均针对该式的参数进行了研究。
国内外大量试验研究表明,钢筋的疲劳性能可用式(2)表示:

式中,Δσ为钢筋的循环应力幅;N为极限循环次数;m,C为常数。
若对式(2)左右两端同时取对数,即得:

式(3)成为钢筋材料经典的疲劳方程形式,并在欧洲各主要规范、美国规范中得到体现。
3 钢筋混凝土受弯构件疲劳方程的建立
钢筋混凝土2种单一材料结合作为一种复合材料后,由于两者之间的共同作用,使得构件层面的疲劳性能与材料层面有所区别本文基于已有素混凝土、钢筋单一材料疲劳性能的研究成果,结合钢筋混凝土受弯构件设计基本原理,从构件层面对钢筋混凝土受弯构件疲劳方程的建立进行一定的探讨。
已有研究表明[5],混凝土受弯构件经多次重复荷载作用,混凝土应变仍呈线性分布,截面平均应变仍符合平截面假定,而且中和轴位置基本不变;且受拉钢筋疲劳断裂时,受压区混凝土边缘的应力远小于静载强度,仍处于线性阶段,试件截面高度的应力分布为三角形(见图1)。根据以上结论,受弯构件承受循环荷载时,最外层钢筋的拉应变与外缘压区混凝土的压应变满足:
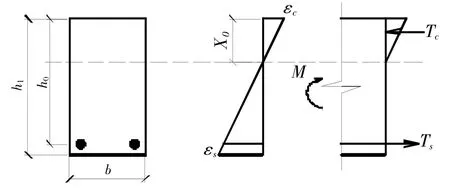
图1 钢筋混凝土受弯构件疲劳计算图式
式中,εs,max,εs,min,εc,max,εc,min分别为同一循环次数下钢筋的最大、最小应变,混凝土的最大、最小应变;h0,x0分别为换算截面的有效高度和受压区高度。
假定循环过程中受拉钢筋、压区混凝土满足弹性状态,即:
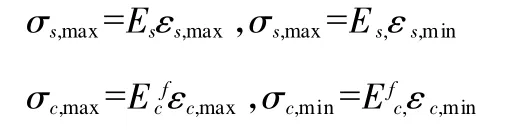
可得:

如将式(5)、式(6)分别代入式(1)、式(3)即可分别得到以钢最大、最小筋应力及混凝土最大、最小应力表示的钢筋混凝土构件的疲劳方程。相关研究表明,适筋梁是由钢筋的疲劳断裂起控制作用,破坏形态为正截面抗弯疲劳破坏[6],且将式(5)、式(6)代入式(1)后即包含钢筋的最大应力及钢筋应力比2个因素,考虑的因素更全面,故此处以纵向钢筋的应力最大应力、应力比建立钢筋混凝土受弯构件的疲劳方程:
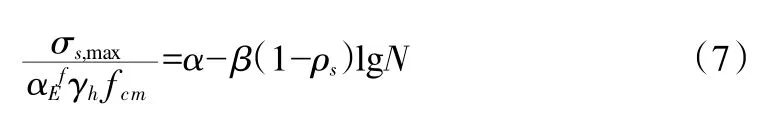
式中,σs,max为钢筋的最大应力;ρs为钢筋的应力比;N为循环次数为钢筋弹性模量与混凝土疲劳弹性模量的比值;γh为与换算截面高度有关的系数;fcm为混凝土静载极限强度;α1,β为参数。
4 与已有疲劳试验结果的对比
为验证以上所提出的方程的准确性,此处将本文计算结果与清华大学李秀芬[7]通过高强混凝土梁弯曲试验得出的结果进行了对比。计算采用的钢筋混凝土矩形梁及参数如图2及表1所示,200万循环次数下的最大应力-应力比关系及最大应力-最小应力关系计算结果与试验结果对比如表2、表3和图3所示。
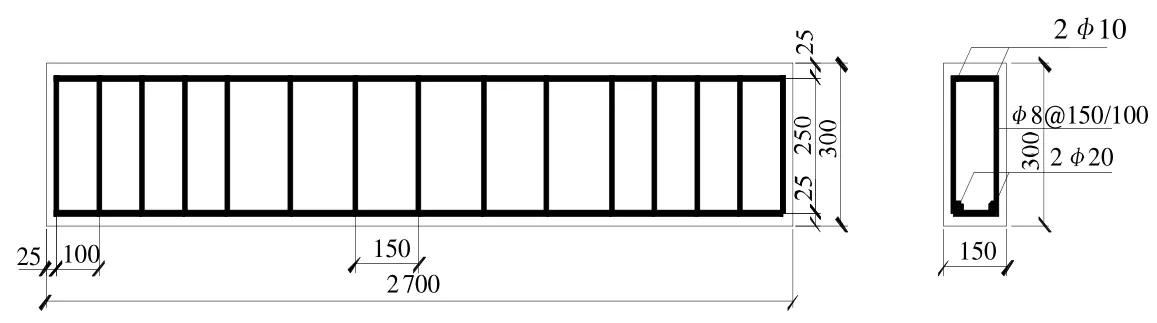
图2 验算用矩形钢筋混凝土受弯构件构造图(C40混凝土,HRB400钢筋)

表1 推导方程在算例计算时所使用的参数

表2 200万次循环次数下最大应力-应力比关系计算结果与试验结果对比

表3 200万次循环次数下最大应力-最小应力关系计算结果与试验结果对比

图3 计算结果与试验结果对比
从以上结果可以看出,本文提出的疲劳方程与李秀芬基于高强混凝土受弯构件的试验结果接近,具有一定的合理性。因已有钢筋混凝土构件疲劳方程的研究成果还十分有限,因而本文提出的方程的适用性和精确度仍需一定的试验验证。
5 结论及展望
1)本文在素混凝土、钢筋单一材料的疲劳方程的基础上,通过引入钢筋混凝土受弯构件平截面假定基本原理,从理论上推导了以钢筋最大应力、应力比表示的钢筋混凝土受弯构件疲劳方程的建立方法;
2)传统钢筋材料疲劳方程中只含应力幅一个变量,此方程不仅包含应力幅,还引入了应力比的影响,考虑因素更加全面;
3)本文建立的钢筋混凝土受弯构件疲劳方程经与已有相关成果对比,具有一定的合理性,但方程尚未考虑配筋率等因素的影响,若要给出更具一般性的普适的钢筋混凝土受弯构件的疲劳方程,仍需大量的试验数据作为依托,这也是当下无法提出钢筋混凝土构件疲劳一般方程的重要原因之一。
【1】宋玉普.混凝土结构的疲劳性能及设计原理[M].北京:机械工业出版社,2006.
【2】高维成.水泥混凝土路面疲劳特性研究[D].西安:长安大学,2000.
【3】石小平,姚祖康.水泥混凝土的弯曲疲劳特性[J].土木工程学报, 1990,23(3):11-21.
【4】陈积光,肖四喜,等.水泥混凝土路面疲劳破坏及其对策研究[J].湖南理工学院学报,2012,25(1):71-76.
【5】朱红兵.公路钢筋混凝土简支梁桥疲劳试验与剩余寿命预测方法研究[D].长沙:中南大学,2011.
【6】贾金青,张丽华,孟刚.钢筋混凝土梁疲劳弯曲损伤指标的计算方法[J].工业建筑,2012,42(8):54-58.
【7】李秀芬,吴配刚,赵光仪.高强混凝土梁抗弯疲劳性能的试验研究[J].土木工程学报,1997,30(5):37-42.
Researchon Fatigue Equationof FlexuralReinforced ConcreteMembersUnder Constant-amplitude Loading
LIU Lei
(CHELBI Engineering Consultants,Inc.,Beijing 100029,China)
Fatigueequationofplainconcreteandsteelhasbeenresearchedalotrespectively.However,consideringtheinteractionbetween thetwomaterials,researchonfatiguebehaviorofthereinforcedconcretecomponentsisstillrare.Basedontheexistingresultsonthematerial levelandthebasicmechanicalprincipleofthesectionofflexuralRCmembers,astudyofthefatigueequationofRCmemberswasconducted, andtheresultswerecomparedwiththatacquiredbysimilarexperiments.
constant-amplitude;fatigueequation;reinforcedconcrete;flexuralmembers
TU375
A
1007-9467(2016)06-0042-03
2016-01-23
刘磊(1986~),男,甘肃庆阳人,助理工程师,从事桥梁结构工程设计与研究,(电子信箱)liulei0905@163.com。

