“遇水架桥”破难点
□
“遇水架桥”破难点
□杨学亮

现实生活中,若遇到水的阻拦,我们会想到架桥通过,那么在解决电学问题时遇到了困难,如果你也会“架桥”,电学问题就会迎刃而解.那么用什么“架桥”呢?这里有两座“桥梁”:涉及简单串联和并联电路的计算,用串联和并联电路中电流、电压、电阻的关系“架桥”;涉及复杂的动态电路的计算,用不变量如电源电压和电阻“架桥”.下面我们一起分析几道例题.
一、简单串联和并联电路的计算
例1(2016·郴州)如图1所示,电源电压为9V且保持不变,R1= 30Ω,闭合开关后,电压表示数为3V,则电阻R1两端的电压为V,电流表的示数为A.
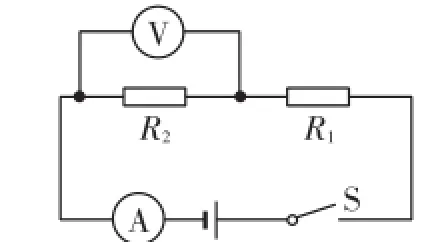
图1
解析:R1两端的电压为

故电流表的示数为
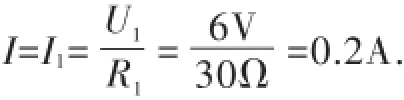
答案:60.2
例2(2016·永州)如图2所示的电路中,电源电压恒定,R2=10Ω,开关S、S1都闭合时,电流表示数为0.4A;开关S闭合,开关S1断开时,电流表示数变为0.3A.则电源电压为_______
V,电阻R1的阻值为Ω________.

图2
解析:开关S、S1都闭合时,R1与R2并联,电流表测干路电流.开关S闭合,S1断开时,电流表测通过R2的电流,电源电压U=I2R2=0.3A×10Ω=3V.
当开关S、S1闭合时,
I1=I-I2=0.4A-0.3A=0.1A,
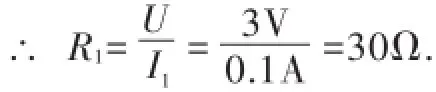
答案:330
点评:在简单的串联和并联电路中,我们常常利用串联和并联电路中电流、电压、电阻之间的关系(串联R=R1+R2,U=U1+U2,I=I1=I2;并联架桥”找出各物理量之间的联系求解.
二、动态电路的计算
例3(2016·厦门)如图3所示,R1=25Ω,小灯泡L的规格为“2.5V0.3A”,电源电压保持不变.
(1)S1、S2都断开时,小灯泡L正常发光,求电源电压;
(2)S1、S2都闭合时,电流表示数变为0.6A,求R2的阻值.
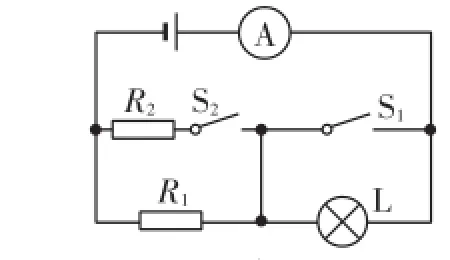
图3
解析:(1)S1、S2都断开时,R1与小灯泡串联,小灯泡正常发光,
故UL=2.5V,
电路中电流I=I1=IL=0.3A,
R1两端电压为
U1=I1R1=0.3A×25Ω=7.5V,
所以电源电压为
U=UL+U1=2.5V+7.5V=10V;
(2)S1、S2都闭合时,灯L被短接,R1与R2并联,电流表测干路电流,通过R1的电流为0.4A,通过R2的电流为I2=I-I1= 0.6A-0.4A=0.2A,故R2的阻值为
答案:电源电压为10V;R2的阻值为50Ω.
点评:动态电路的计算,要先看清不同状态下电路的连接方式,分别找出不同状态下电压、电流、电阻之间的关系,再利用不变量(比如电源电压、电阻)“架桥”,将不同状态下的各物理量联系起来求解.

