多相位齿轮啮合有限元分析
孙成龙,许军辉,崔瑾
(1.长城汽车股份有限公司技术中心,河北保定 071000;2.河北省汽车工程技术研究中心,河北保定 071000)
多相位齿轮啮合有限元分析
孙成龙1,2,许军辉1,2,崔瑾1,2
(1.长城汽车股份有限公司技术中心,河北保定 071000;2.河北省汽车工程技术研究中心,河北保定 071000)
齿轮强度分析是齿轮设计过程中的重要环节。运用有限元方法先对齿轮进行单一相位的分析,得到齿根的最大主应力,然后提出一种齿轮啮合多相位静态分析方法,得到齿轮啮合过程中齿根最大应力的变化曲线。由分析结果可知,多相位分析方法较单一相位分析方法更精确可靠,且比动态仿真分析节约资源和时间,为齿轮静强度分析提供了参考。
齿轮啮合;多相位;有限元;齿根应力
0 引言
变速器的品质对汽车动力性、经济性、操纵性等有直接影响。齿轮作为汽车变速器的关键零部件,在变速和变载的复杂工况下工作,常处在高温和动载等条件较差的工作环境,易损坏,因此齿轮质量关系着变速器能否平稳高效地运转。近年来,随着变速器向小型轻量化方向发展,对变速器齿轮强度分析与评价提出了更高的要求。
随着科学技术的发展,有限元法和边界元法开始获得应用。有限元法(Finite Element Method,FEM)是一种离散化数值分析方法,它将一个结构看成是有限单元组成的集合体,单元通过有限节点链接,具有有限自由度,使计算分析成为可能。与传统方法相比,有限元法能准确获得齿轮的真实应力场,可以为齿轮强度分析提供可靠依据,有利于对齿轮传动过程中的力学特性进行深入研究。关于齿轮啮合有限元分析方法的研究国内学者做了大量工作。
静态方面,文献[1] 中基于有限元法的基本原理,利用有限元软件,对齿轮进行接触分析,计算出齿根的最大应力;文献[2]中研究了网格密度、单元类型等因素对齿轮啮合强度及接触应力的影响;文献[3]中应用有限元分析软件ANSYS得到了齿轮齿条啮合时的变形及齿根应力。但是在齿轮强度静态分析中,大部分只进行了单一相位的分析,齿根弯曲应力无法保证为最大值,且主、从动齿轮最大应力出现的位置不一定在相同相位,因此单一相位的分析结果不够精确。为保证得到的齿根弯曲应力为最大值,提高分析准确性,需对不同相位下齿根弯曲应力进行研究。
动态方面,文献[4-5]中对准双曲面齿轮的动态啮合性能进行了研究,得到啮合接触冲击特性、齿面接触区域、齿面接触应力及齿根弯曲应力等在轮齿动态啮合过程中的变化规律;文献[6]中研究了考虑滑动摩擦、齿廓修形及时变刚度等因素的齿轮副低速和高速工况下连续弹性啮合过程的动态啮合特性。大部分齿轮啮合动态分析主要集中在冲击性能方面的研究,虽然在稳定阶段可以得到啮合过程中齿根应力的变化曲线,但需要耗费大量资源和时间。
作者从工程实用角度出发,提出了一种齿轮啮合多相位静态分析方法,比单一相位静态分析方法更精确可靠,与齿轮啮合动态分析相比节约了大量资源和时间。
1 仿真模型
利用三维设计软件对齿轮啮合几何模型进行精确建模,如图1所示。其中齿轮的基本结构参数如表1所示。
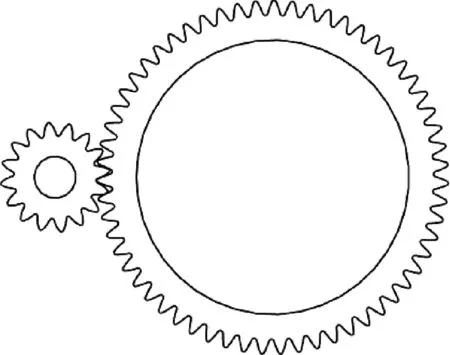
图1 齿轮几何模型

表1 齿轮结构参数
在有限元分析中,单元类型的选择对结果有很大的影响。对齿轮进行网格划分时,采用四面体单元划分网格虽然能够自适应齿轮的复杂齿廓,容易实现接触带局部网格细化,但是有限元模型的节点和单元规模极为庞大,计算效率低。采用六面体单元虽然可以实现齿轮映射网格划分,但是若使整个齿轮具有相同高密度的网格分布,有限元模型的节点和单元规模仍然极为庞大。因此,文中整体进行六面体单元映射网格划分,只在接触及齿根部位采用细化网格,而远离关注的位置采用较粗的网格并使用三棱柱单元过渡,能够有效解决齿轮啮合有限元分析中计算精度与计算效率之间的矛盾。完成的有限元模型如图2所示。

图2 齿轮有限元模型
2 单一相位静态分析
单一相位齿轮啮合静态分析主要是通过固定一个齿轮,在另一个齿轮上施加相应转矩,并在相接触的齿面间设置接触对的方法进行分析。具体参数如表2所示,加载约束示意图如图3所示。

表2 单一相位静态分析的详细参数

图3 单一相位静态分析的加载约束示意图
计算完成后,可以在后处理中查看齿轮啮合分析的结果,图4给出了一对齿轮的最大主应力分布云图。可以看出:大小齿轮的最大应力均发生在齿根部位,这与实际工作情况是符合的,且最大应力的数值分别为大齿轮577 MPa、小齿轮402 MPa。
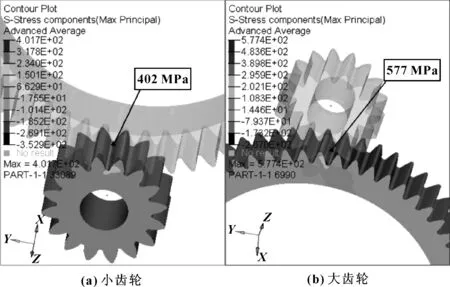
图4 最大主应力云图
3 多相位仿真分析
由于不能保证单一相位静态分析中得到的最大应力值是齿轮啮合过程中的最大值,因此需要对不同相位下的齿轮进行分析。如果进行动态啮合分析,虽然能够得到齿根应力的变化曲线,但是由于在分析开始存在冲击,需要较长时间才能达到稳定阶段,将耗费大量时间。文中通过在静态模块中设置强制旋转位移和自动接触的方法实现静态分析动态模拟齿轮啮合过程的效果。采用文中所用分析模型,在相同电脑配置情况下,多相位静态分析相比动态分析将节约近30%的时间。

表3 多相位仿真分析的详细参数
根据表3中所列的分析方法和详细参数对模型施加边界条件和约束,如图5所示。与单一相位静态分析相比,需要注意以下几个方面:
(1)边界条件。保证加载扭矩大小和位置不变,方便后期对比,将固定的小齿轮释放轴向旋转自由度并施加强制旋转位移,达到模拟动态分析的效果。
(2)接触对设置。接触对中除了需要包括初始状态接触的齿面以外,还应加入在旋转过程中可能接触的所有齿面(根据强制旋转位移大小确定)。
(3)大变形及步长。需要像动态分析方法一样打开大变形选项,并且控制步长大小,需要足够的子步才能准确地模拟一对齿从啮入到啮出的过程,文中设置了100个子步。
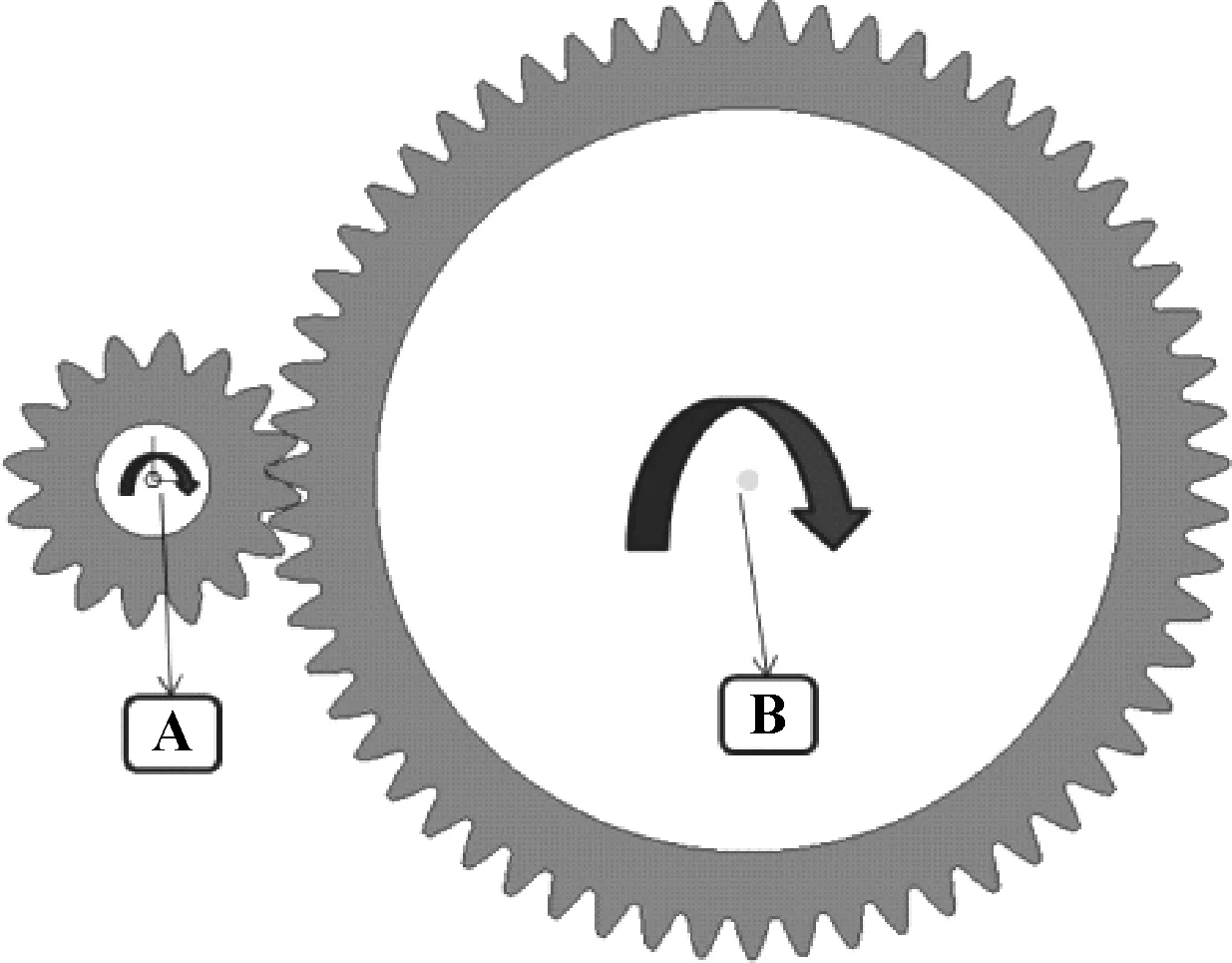
图5 多相位仿真分析的加载约束示意图
图6所示为小齿轮上提取的反扭矩变化曲线,通过速比可以得到小齿轮扭矩为250 N·m,图中的曲线在250 N·m附近波动,证明计算过程和加载方式的正确性。

图6 小齿轮上的支反扭矩
图7所示为一对啮合齿的最大主应力云图及齿根最大应力随啮合过程的变化曲线,对比单一相位和多相位静态分析不难发现,多相位分析相当于是多个不同相位静态计算结果的累加,可以通过设置分析步长或时间来控制相位的变化量。同时,从图7中得到齿轮啮合过程中齿根应力的最大值分别为大齿轮585 MPa、小齿轮565 MPa,与单一相位静态分析有较大的差别;且可以看出:大齿轮和小齿轮的齿根最大应力值不是出现在同一时刻,存在相位差,这与实际啮合过程相符。

图7 最大主应力云图及变化曲线
4 结论
首先完成了齿轮啮合单一相位下的静态分析,针对不足提出了多相位静态仿真分析方法,并对两种方法进行了比较。通过以上分析,得到如下结论:
(1)单一相位下齿轮静态分析虽然能得到齿根应力,但是不能保证是啮合过程中的最大值,与所选的啮合相位有关。
(2)多相位分析方法能得到齿轮啮合过程中齿根应力的变化曲线,因此能确定齿根应力的最大值及最大值出现的啮合位置,且主、从动齿轮齿根的最大应力不在同一相位。
(3)多相位静态分析相比动态分析没有初期的冲击影响,因此可以节约大量资源和时间,同时能得到齿根应力的变化曲线,为齿轮设计中强度的校核提供新的参考。
【1】符双学,田巍,李长云.基于有限元法的齿轮强度接触分析[J].长沙航空职业技术学院学报,2009,9(2):45-49. FU S X,TIAN W,LI C Y.Contact Analysis of Gear Strength Based on Finite Element Method[J].Journal of Changsha Aeronautical Vocational and Technical College,2009,9(2):45-49.
【2】郝东升,王德伦.斜齿轮精确接触分析有限元建模方法[J].大连理工大学学报,2011,51(6):825-831. HAO D S,WANG D L.An Approach to Building a FEM of Helical Gears with Accuracy Contact Analysis[J].Journal of Dalian University of Technology,2011,51(6):825-831.
【3】陆静静,柳强.齿轮齿条强度应力有限元分析[J].汽车实用技术,2016(4):21-23. LU J J,LIU Q.The Finite Element Analysis of Strength Stress for Rack and Pinion[J].Automobile Technology,2016(4):21-23.
【4】唐进元,彭方进.准双曲面齿轮动态啮合性能的有限元分析研究[J].振动与冲击,2011,30(7):101-106. TANG J Y,PENG F J.Finite Element Analysis for Dynamic Meshing of a Pair of Hypoid Gears[J].Journal of Vibration and Shock,2011,30(7):101-106.
【5】曹茂鹏,唐进元,雷敦财.直齿-面齿轮动态啮合力有限元仿真分析[J].机械传动,2015,39(4):96-101.
【6】吴勇军,梁跃,杨燕,等.齿轮副动态啮合特性的接触有限元分析[J].振动与冲击,2011,31(19):61-67. WU Y J,LIANG Y,YANG Y,et al.Dynamic Meshing Characteristics of a Gear Pair Using Contact Finite Element Method[J].Journal of Vibration and Shock,2011,31(19):61-67.
【7】庄茁,张帆,岑松,等.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005.
【8】石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.
Finite Element Analysis of Gears Meshing under Multi-phases
SUN Chenglong1,2, XU Junhui1,2, CUI Jin1,2
(1.Research & Development Center of Great Wall Motor Company, Baoding Hebei 071000,China;2.Automotive Engineering Technical Center of Hebei, Baoding Hebei 071000,China)
Gear strength analysis is the important part of gear design project. Based on finite element method, the gears meshing static analysis under a single phase was achieved, and the maximum principal stresses of gears root were obtained. Then, a gears meshing static analysis method under different phases was provided, and the maximum principal stresses curves of gears root in the engaged and disengaged process were obtained. Study shows that static analysis method under different phases is more accurate and reliable than under a single phase, and it saves more resource and time than dynamic analysis.It provides reference for gear strength design.
Gears meshing; Multi-phases; FEA; Stress of gear root
2016-09-06
孙成龙(1988—),男,硕士,主要从事CAE仿真分析工作与研究。E-mail:chlsun@163.com。
10.19466/j.cnki.1674-1986.2016.12.006
U463.2
A
1674-1986(2016)12-028-04

