高一函数学习中的认知障碍研究

王康

(吕梁学院汾阳师范分校，山西汾阳 032200)

高一函数学习中的认知障碍研究

王康

(吕梁学院汾阳师范分校，山西汾阳 032200)

从数学认知结构发展的角度，研究分析了高一学生函数学习过程中的认知障碍，主要有函数科学概念的认知和知识迁移两个方面。日常教学中要将教师的“导”与学生的“悟”有机结合，以促进函数认知结构及相应图式的动态生成。

数学认知结构;高一函数;认知障碍

函数概念因其高度的抽象性成为高中生普遍感到最难把握的一个概念，也是老师普遍感到最难教的一个概念，而高一学生在经历了初中阶段函数“变量说”之后，紧接着要从集合对应的角度重新理解函数，认知结构被重新定义，造成高一新生函数学习的不适应，具体表现为课堂上听讲似懂非懂，课后做题错误率很高。

现代认知学习理论认为，数学学习过程是学生作为教学活动的主体，在教师的主导和指导之下，动态构建数学认知结构，而不是在头脑中进行数学知识的简单堆砌。基于此，我们从数学认知结构及其特征出发，具体分析研究高一学生函数学习中的认知障碍，以期从本质上解决函数教学中存在的问题。

1 数学认知结构

数学认知结构概念最早是由曹才翰先生提出的，其后的不少研究者结合自身理解提出了不同的表述，湖北大学刘斌老师在《数学认知结构及其建构》［1］一文中提出，数学认知结构既包含处于底层的数学、概念、定理等，又包含处于中间层次的数学方法和解题技巧，还有处于高层次的数学方法论和数学观。同时，还是一个带有能动性的、具有开放性的、立体多层次的、网状的知识结构。此外，根据皮亚杰关于一般认知结构的学说，数学认知结构还具有整体性、转换性和自我调整性。

2 函数认知障碍

2．1 概念认知的障碍

数学认知结构的整体性是指学习主体内化相关概念、定理以及自身的理解成为一个有机整体，与原有的数学知识不断沟通，使之同化在原有的认知结构之中，形成新的认知结构整体(“知识块”)。初高中阶段的函数概念是从两个不同的角度分别描述的，高一学生对函数概念的认知是建立在初中阶段函数“变量说”之上的，同时还要理解函数概念中辩证的哲学思想、数学方法、其他函数概念，进一步形成基于“对应说”的新的认知结构。

数学和哲学是两个人类思维成就最高的领域，哲学思想指导着数学的发展，数学思想丰富了哲学的观点，二者之间紧密联系，函数概念本身蕴含着丰富而深刻的哲学思想。具体体现在如下几个方面:第一，事物间联系的普遍性，函数概念就是建立在大量现实世界中的实例之上，抛去个别非本质的因素而留下共性的自变量、因变量、对应关系，进而抽象成一个数学模型，揭示变量间的相互依存关系和对应关系，即但凡有联系的两个量，就很有可能存在某种函数关系，这种函数关系不一定必须用函数解析式来表达，也可以使用图形、表格、或对应符号f等方式进行表达;第二，事物内部的矛盾性，事物对立而又统一的矛盾双方推动着事物的变化发展，对立统一规律是唯物辩证法的根本规律，函数中数与形的对立统一，变量与常量的对立统一，特殊和一般的对立统一等均是培养学生的辩证思维，多个方面不同角度更好的认知函数概念本身;第三，事物发展的否定之否定推动着事物不断完善和发展自己，否定之否定是唯物辩证法的基本规律之一，函数概念的产生和发展即是如此［2］，函数概念的发展从最初几何观念下的研究到变量说，再到后来的对应说以及集合论观点下的映射研究，推动着概念本身不断完善，初高中学生对函数概念的认知过程就是在这样一种否定之否定的过程中，认知结构得到不断的完善和扩充，例如，初中生看待y=1只是一个普通常量或是某方程的解，而高中生要从集合对应的角度，它可以看做是一个多对一的函数，也可以是一次函数y=kx+b中系数k，b特殊化的结果。

然而，高一学生的思维发展水平尚处于一个关键的过渡时期，由具体形象思维水平逐步过渡到形式逻辑思维水平，并逐渐脱离对感性经验的依赖，侧重逻辑推导。高中阶段在继续完善形式逻辑思维的前提下，逐步发展抽象逻辑思维，唯物辩证的看待事物的发展变化［3］。

可见，根据高一学生现有的思维水平，要求他们辩证的看待函数概念中数与形的紧密联系、变量与常量的对立统一、具体与抽象的相互转化、初中不成熟的概念认知等还为时尚早，需要在以后的学习中不断体会。

2．2 知识迁移的障碍

前苏联著名的教育学家苏霍姆林斯基曾说，教学是教给学生借助已有知识去获取新知识的能力，并使学习成为一种探索活动。同时，学习也是一个连续的过程，新的学习总是建立在先前学习的基础上，新问题的解决总是受到先前问题解决的影响，这就是知识迁移，迁移是人类认知的普遍特征，它广泛存在于知识、技能与行为规范的学习中，贯穿于整个学习过程，是学习中最重要的现象之一，属于教育心理学研究的范畴［4］。

首先，迁移的本质是抽象的过程，越是抽象的知识，可迁移的范围就越广，学习迁移的跨度也越大，比如函数思想贯穿于整个高中数学阶段，并延伸至大学阶段;其次，迁移的基础是联系，只有有联系的知识才能产生迁移，比如，函数与不等式、函数与方程都可以用图像联系，从图像上认识这些问题，也是数形结合思想的具体应用;第三，迁移的实现是联想，只有从问题联想到已经掌握的知识和技能，才能找到解决问题的策略。以下从两个方面指出学生在知识迁移时的障碍对函数认知结构建构的影响。

2．2．1 教学前概念和经验

在日常生活和以往的学习(初中)中，学生对一些数学问题和现象有了自己的看法和理解，这些看法和理解是新概念赖以建构的基础，我们称之为教学前概念(Pre-instruction)［5］。还有，Duit (1994)把学生在教学新概念之前就已持有的概念称为教学前概念，主要包括错误概念(Mis-Conception)和前概念(Pre-Conception)，错误概念是指学生在长期的学习中形成的对概念错误的理解，前概念是指源于先前学习中对科学概念的一些浅层次的认识。

我们知道，函数概念的学习分为两个阶段，初中阶段函数的定义是建立在“某个变化过程中”的两个变量，并且他们在变化过程中有一个显性的关系式，而高中阶段的函数定义是建立在“A，B两个非空的数集”之间某种确定的对应关系，即函数是两个集合之间对应关系，并且有时的对应关系是隐性的，用f来表示，这样就产生了认识上的不一致，造成了函数抽象性的根源。另外，学生的思想认识中基于初中函数概念的理解是浅显的，有些甚至还是错误的。比如错误的以为函数就是变量y，y是经过一个算式计算而来的，或者把函数理解为一个具体的算式，这样的理解就把函数的三要素孤立的看待，是浅层次的认识。此外，对于高中形式化、符号化的表达方式也不能正确认识，如无法感受到f(x)=ax+b带来计算和表述上的优越感。此外，函数性质的学习之前，初中阶段已经对图形的升降、对称做过感性研究，有一定的认识经验，高中阶段是从科学理性的角度做深层次的定性研究。

正确看待教学前概念对高中函数学习的影响，促进知识迁移，形成正确图式。要求我们在日常教学中，要了解学生已有的知识经验，促进教学前概念向科学概念的转变;也可以根据学生先前形成的错误认识引发认知冲突，辨清分歧所在，转变重组自己的已有观念;注重函数诸多概念间的相互联系，在概念形成的网络中全面理解函数对应说的本质，重视概念生成的凝聚，加快函数概念从“过程”向“对象”的转化。

2．2．2 概括加工水平及意识

学习迁移的概括说是早期迁移理论中非常经典的理论之一，是美国心理学家贾德提出的，他认为从经验中学到的原理是迁移发生的主要原因。学习者在前期学习A中所获得的知识，之所以能够迁移到后期的学习B中去，是因为在学习A时获得了一般原理C，这种原理C可以部分或全部运用到A、B之中。迁移产生的关键是学习者在两种学习中概括了他们的共同原理，这一理论可以形象地用下图表示。

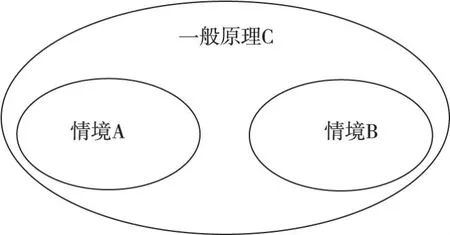
迁移概括说模型

对数学材料概括的几种形式主要有强抽象概括模式、弱抽象概括模式、广义抽象概括模式，所共同的心理过程有观察、联想、归纳、抽象、识别等，原理的概括过程即为思维的抽象过程，是一个构建网状知识结构的过程，促进图式的形成和认知结构的发展。长期的教学实践表明，掌握原理的学习比机械学习的效果好，掌握原理的同时又了解原理应用的实际情境效果会更好。从近几年高考试题可以看出，考查的基础知识、基本技能、基本方法，强调的是通性通法，淡化解题特殊技巧，避免题海战术!例如，比较两个数值的大小关系，应该是抽象出一个函数通过单调性来讨论之，此为站在理性思维的高度的通法。再如，函数的定义域问题关键是要找到与自变量x所处的位置，位置一样即所对应的范围也一样，因为运算是函数的一个基本属性，在解析式已知的情况下，y =与y=

3 结论

数学是思维的体操，学生思维层次的提高体现在认知结构的不断完善，高一学生在函数学习过程中面临的所有问题可以归结为两个方面:第一，高一学生现有的思维发展水平和辩证的函数概念之间的矛盾构成了概念学习、理解、甚至于应用的一切障碍;第二，解题者对数学问题的抽象和方法的归纳总结，能否从一般原理的角度认识看待函数问题，实现知识的正迁移。

我们要清醒的认识到学生掌握函数的科学概念绝非一朝一夕可以一蹴而就的，日常教学应该遵循中学生思维发展的客观规律，学生理解函数概念是需要反复多次的，其认知结构的建立亦是一个螺旋上升、动态生成的过程，而对于学生思想中的错误认识，可以采用过度延伸策略，引发认知冲突，重组自己的已有观念，促使学生认知结构的同化和顺应;其次，解题教学中教师应注重思想方法、通性通法的介绍，注重知识间的前后联系，避免题海战术，如:方程x2=x0，|x|=x0，sinx=x0的根为什么都是两个且具有某种对称关系?不等式的基本性质和函数单调性之间的有何联系等等。总之，将教师的“导引”与学生的“感悟”有机结合。循序渐进的理解函数概念的二重性，促进函数概念从“过程”向“对象”的转变。

［1］刘斌．数学认知结构及其建构［J］．湖北大学学报(自然科学版)，1997，19(3)．

［2］王康．高一数学函数抽象性教学研究［D］．山西:山西师范大学，2014．

［3］朱文芳．函数概念学习的心理分析［J］．数学教育学报，1999，11，8(4)．

［4］吴庆麟．认知教学心理学［M］．上海:上海科学技术出版社，2000:209-233．

［5］周友士．基于建构主义的数学概念转变学习［J］．数学教育学报，2004，8，13(3)．

［责任编辑:陈业强］

Analysis of the cognitive barriers instudying function for the first grade of senior high

WANG Kang

(Fenyang Teachers’School Branch，Lvliang University，Fenyang，Shanxi，032200)

From the perspective of cognitive structural development，this paper analyzes the cognitive barriers in studying function for the first grade of senior high，which include the cognition of the concept of function and knowledge transference．The study suggests that teachers’“guidance”and students’“understanding”should be combined properly in the daily teachingto promote the cognitive structure of function and the dynamic generation of the corresponding schema．

Cognitive structure in mathematics;Function for the first grade ofsenior high students;Cognitive barrier

G633．6

A

1674-7798(2016)09-0082-03

10.13391/j.cnki.issn.1674-7798.2016.09.017

2016-08-29

王 康(1982-)，男，山西芮城人，讲师，教育硕士，研究方向:基础数学学科教学。