基于软时间窗的车间物料配送调度优化研究

李加玲，钱吴永

（江南大学 商学院，江苏 无锡 214122）

基于软时间窗的车间物料配送调度优化研究

李加玲，钱吴永

（江南大学 商学院，江苏 无锡 214122）

实际生产中车间内部工位物料需求存在一些不确定性问题，基于软时间窗的概念提出车间内部物料配送调度优化的方法。在已给定的假设基础上，研究带有时间窗的车间物料配送问题，将配送总时间最短作为目标函数，建立关于车间物料配送调度的数学模型，采用一种改进的遗传算法对模型求解，得到车间物料配送的最佳路径。最后通过实例验证该模型的有效性。

物料配送；软时间窗；遗传算法；调度优化

1 引言

近年来，企业生产智能化水平逐渐提高，制造企业间的竞争日趋激烈。客户的需求出现“多样化、小众化、个性化”的发展趋势，为了适应这种变化趋势，多品种小批量的生产模式日趋引起关注和重视。这一变化增加了对产品制造柔性的要求，也对车间物料配送提出了新要求。一方面，多品种小批量生产产品种类多，数量少，导致了物料的数量不易控制，引起了广大学者对车间内部物料流关注，尤其是物料配送方面的研究。李晋航建立模糊信息条件下的机会约束规划模型，采用启发式算法处理不确定因素，提高物料配送的可行性和高效性[1]。刘明周基于生产计划、节拍、库存等不确定因素，构建RTMADS系统，阐述系统架构，对物料配送各环节数据实时监控[2]。凌琳考虑制造工位的生产能力与生产负荷间的关系，用两者比值表征物料配送的迫切度，构建改进的时变的物料配送路径模型，并考虑将物料拆分配送，提高配送效率[3]。

另一方面，工位物料需求时间的不固定，吸引了不少国内外的学者聚焦于车间内部带时间窗的物料配送工位需求的研究。车间内部工位需求的问题相当于是缩小的车辆路径问题，将车辆路径的研究范围缩小到车间内部。antzig和Ramser（1959）对带时间窗的车辆路径问题（vehicle routing problems with time windows，VRPTW）进行了研究。此后，许多研究人员对车辆路径问题展开了较为系统的研究，构建各种优化模型，用优化的智能算法对模型进行求解应用。Muller运用两阶段启发式算法，结合新型遗传模拟退火算法，研究带时间窗的车辆调度，并考虑违反时间窗的惩罚函数，控制总成本最小[4]。王旭坪等将时间窗的处理模糊化，用物料配送起始时间的模糊隶属度函数将顾客服务的满意度量化。建立模糊时间窗的车辆配送模型并通过实例验证模型在维持顾客服务水平、节省企业资源等方面的有效性[5]。BANOS等基于平行多目标模拟退火遗传算法来解决带时间窗的车辆调度问题，考虑了最大限度地减少车辆的行驶距离和线路的不合理多目标约束并构建模型，采用实证验证模型的有效性[6]。Kilic考虑带有软时间的车辆路径问题时，构建一个模糊规划处理顾客的偏好以及最新交货时间公差，更易权衡分销商的效率和反应谱[7]。章勋宏等对考虑零件三维装载约束带时间窗的循环取货路径问题展开研究，建立多目标数学模型，大幅提高可装载性，减少不同车型车辆的投入[8]。也有研究人员将车辆路径问题引入到制造车间内部物料配送方面，研究车间内部物料配送，保持高效运作，节约时间和成本，提高车间的生产率。如Androutsopoulos主要考虑危险材料的路径调度决策，假设成本和风险随时间变化，提出路径的调度问题涉及测定非支配时变路径和在规定的时间窗内为客户提供中间站服务，讨论了解决这类问题的两种算法[9]。Gao Gui-bing等构造了混合制造系统中的物料配送路径问题的多目标模型，采用混合多目标进化算法求解，通过实际案例研究表明，该模型可以减少总行驶距离，提高车辆的平均负载率[10]。严正峰等提出模糊软时间窗的概念，在此概念基础上研究车间物料流路径优化方法，主要以工位为中心安排物料配送，建立带软时间窗的物料配送路径优化模型，结合智能算法求解[11]。Simic等介绍了关于物流配送的车辆路径问题的建模与优化，建立一种新的混合模型，运用包括遗传和萤火虫算法求解得到实验结果，并与真实数据比较，验证模型求解的结果更好[12]。

现有文献中对物料配送的研究，主要包括物料的管理控制、配送路径优化等方面，而车辆路径问题的研究主要集中在较大型的物流运输方面，从成本、时间以及行驶路程等角度考虑，寻找最优路径。近年来，有学者开始将宏观的车辆路径问题的研究方法和思路应用到制造业内部物料流分析中，主要研究制造业内部物料配送路径问题，求解制造业内部物料配送的最优路径，缩短时间，提高生产效率。本文基于现有的研究，结合软时间窗的概念，将车辆路径问题用到车间内部物料配送上，以时间最小化为目标，同时考虑到物料在时间窗之外到达时，构建相应的惩罚函数。本文将时间最短作为目标函数，寻找最优的车间物料配送路径，是考虑到车间内部的物料运输通常都是用叉车运输，且每条路径行驶的路程较短、差距较小，所需成本差别也较小，可以忽略。所以选择时间最小化为目标是更加符合车间内部物料运输的实际情况。

2 模型构建

2.1 问题的描述

关于车间内部物料流的车辆路径问题的描述：车间内部各工位所需要的物料都储存在统一的仓库，这里称之为物料超市，工位所需物料都由物料超市负责运输配送，由k个承载量为q的车辆负责将物料配送到需要的各工位，车间内有N个工位，各工位上所需的物料要在时间窗之间被送到。考虑到物料有可能会在时间窗之外被送达，本文基于软时间窗的车间物料配送调度进行研究，如果物料不在规定的时间窗之内送达，建立相应的惩罚函数。考虑到车间内部物料的配送都是以叉车为主，且车间内部的行驶距离较短，因此，车辆的油耗差距小，当叉车的速度一定时，若配送时间短，则车子的行驶距离就短，且人力的消耗最小，因此，可以将车间内部物料配送路径优化问题转化为求车间内物料配送时间最短的车辆行驶路径。

2.2 工位物料配送模型假设与约束条件

2.2.1 假设条件。为了使研究问题更加明确，现对模型做如下假设：

物料超市所提供的物料种类、数量等信息已知，各工位所需要的物料品种、数量也已知。且配送到各工位的物料都是由一个物料超市负责提供。

各工位所需的物料量之和不超过物料超市的储存量。

物料超市到每个工位的距离、各工位之间的距离均已知。

假定车辆的行驶速度已知且匀速行驶，因此派出取物料的车辆在各工位节点之间以及物料超市到各工位的行驶时间可以直接求出。

2.2.2 约束条件。（1）物料配送时，车辆从物料超市出发到各工位进行物料配送，当车辆重新回到物料超市表示一个物料配送路径结束。

（2）根据物料需求将工位分为多个工位组，一辆车对一个工位组所需要的物料进行一次或多次配送。

（3）一个工位组需要的所有物料都储存在一个物料超市里，而一个物料超市可以储存多个工位组需要的物料。

（4）一个工位组所需要的物料由一辆车负责配送。

（5）一个工位组一次所需要的物料量不能超过一个物料超市的最大储存量。

（6）每辆车的行驶距离须在其规定的最大行驶距离之内。

2.3 参数符号

（1）已知量

i,j∈N：表示需要被服务的工位的编号；

k：表示负责配送的车辆的编号；

ti：车辆到达服务的工位的时间；

te：物料配送到达工位的时间窗的开始时间；

tl：物料配送到达工位的时间窗的结束时间；

wi：为服务工位i所需要的等待时间；

si：在工位i装卸货的服务时间；

dij：工位i到工位j之间的距离；

v：车辆的平均行驶速度；

Q：车辆的最大载重量；

L：车辆行驶的最大距离；

M,N：工位组的编码；

qik：车辆需k要向工位i配送的物料量。

（2）决策变量。为了方便物料配送模型建立与求解，根据车间内部物料配送的实际情况对模型做了一些简化处理，如下：

2.4 模型建立

多品种小批量制造车间的物料配送调度主要研究的是物料配送效率的提高，主要反映在如何优化求解可以使得一次物料配送的总时间最短。若车辆在提前或滞后到达工位，建立惩罚函数如下：

其中α，β是车辆在时间窗之前和在时间窗之后到达的惩罚因子是指车辆在时间窗之前和时间窗之后到达工位的不满意度。

根据以上分析构建的从物料超市到工位物料配送时间最短的目标函数如下：

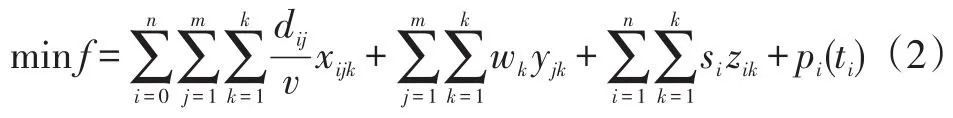
其中：

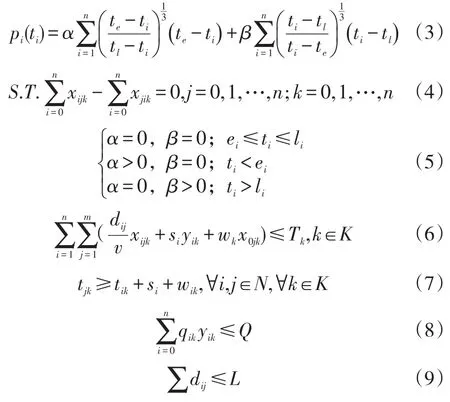
在上述表达式中，公式（2）为所构模型的目标函数，完成物料配送的总的服务时间最短为目标函数。主要由四部分组成是车辆行驶时间（从物料超市到各工位）是求在物料超市排货、拣货、装卸货的等待时间是在工位站点装卸货物的服务时间；pi(ti)是车辆在超出工位规定的时间窗达到工位的一个惩罚函数，如果车辆在工位设定的时间窗之内到达，惩罚函数pi(ti)为0，到达时间在工位设定的时间窗之外时则考虑惩罚函数。其中α，β是车辆在时间窗之前和在时间窗之后到达的惩罚因子。如果车辆在工位设定的时间窗之前到达，其惩罚函数为如果车辆在工位设定的时间窗之后到达，其惩罚函数为

约束（4）保证每个工位上到达的车辆和离开的车辆的数量相等。约束（5）表示的是工位时间窗的限制，即工位可接受的物料到达的时间范围。约束（6）约束的是所有物料的配送需要在一定的时间内完成。约束（7）是车辆从工位i到工位j的过程中，对其服务时间前后的约束。约束（8）保证车辆的装载量在其最大载荷之内。约束（9）是限制车辆的行驶距离须在其规定的最大行驶距离之内。

传统的路径优化模型一般都是在大型的物流运输中的，构建目标函数时都是以成本最小化为目标，也有以成本、时间为目标构建多目标函数的。本文所构建的模型是针对车间内部物料流的，车间内部物料运输都是叉车运输，其各路径的行驶路程较短且接近，人力成本、能源消耗相差都较小，所以以成本最小化为目标函数不太符合实际情况。本文在构建模型时之所以选择时间最小化作为目标函数，是因为时间对于车间内部物料配送而言较重要，物料到达工位的时间对生产会有很大的影响，提前和延后都会对生产线产生影响，只有在规定的时间窗之内到达才是最佳的。因此，对在时间窗之外达到的物料构建了相应的时间惩罚函数，更加符合车间内部物料配送的实际情况。

3 模型求解

本文的研究主要是制造业内部物料流的物料配送调度问题，该问题的关键是确定从物料超市到工位组的路线安排，考虑带有软时间窗的车间内部物料的配送，在物料储存确定的基础上，将物料配送调度问题转化为一个时间最短问题，寻找最优的车间内部物料配送路径。解决这类问题最常用的方法就是建立相应的目标函数，用遗传算法等智能算法对目标函数求解，得到最优的物料配送路径。

遗传算法求解带时间窗约束的车间内部物料配送路径的步骤如下：

STEP1：构造满足上述模型中约束条件的路径染色体。由于解空间中的解遗传算法不能直接处理，要通过编码用适当的染色体将解表示出来。对于实际问题，染色体的编码方式多种多样，在选取染色体的编码方式时应选取符合约束条件的，否则会影响计算。

本文求解的是带时间窗的VRP问题，采用实数编码是求解时的最直接、最容易实现的方式。可以用每个基因表示每个需要服务的工位，一组基因代表一条配送路线，各路线之间用0隔开，0表示物料配送超市。例如：012305768490这样的染色体编码，表示共有9个工位有物料配送的需求，分为3条配送路线。这3条配送路线的安排如下：

路径1：物料超市→工位1→工位2→工位3→物料超市；

路径2：物料超市→工位5→工位7→物料超市；

路径3：物料超市→工位6→工位8→工位4→工位9→物料超市。

在该染色体编码中各路径内是有顺序的，如路径1中工位1和工位2之间位置互换的话，会导致最后目标函数的值发生改变；而编码的各子路径之间是无序的，如上述的路径1和路径3的位置互换，是不会对最终目标函数的值产生影响的。即0123057068490和0570123068490是没有区别的。

STEP2：产生随机初始群体。搜索开始的一组染色体为初始种群，其数量也就是种群规模需要适当进行选择；

考虑到带时间窗的车辆路径问题较特殊，按照传统的随机排列方式所生成的染色体，会导致大部分都不满足时间窗的约束。因此，本文为了更方便地求出可行解，采用一种赌轮启发式算法寻找可行的物料配送路径。具体步骤如下：

（1）所有的需要进行物料配送的工位都安排完毕，结束（1），否则转（2）；

（2）选中已选择的点，若之前未有选定，那么即为物料超市。将所有还没有被安排的工位与该点连接，将符合约束条件的路径（约束包括时间窗约束，车辆最大载重约束）保留，用路径的长短表示评价保留的路径值。如果没有一条符合条件，这条线安排完毕，选择下一辆服务的车，起始点还是物料超市，转（2）；所有车辆安排完毕，转（3）；

（3）采用轮盘赌的方式对保留的路径进行高低排列、区域划分，路径值越高，其所占有的区域值就越大；

（4）旋转一次赌轮，选出一条符合条件的路径，其它路径都删除，而选中的点为下一个起始点，返回（1）。

每执行一次，可以得到一个车辆路径计划方案，将该方案当做一个可行染色体，然后重复执行，得到多个不同的可行染色体。进而得到初始种群。

STEP3：计算每个染色体的适应度eval(xi)。寻找适应度最大的染色体；

构造的适应度函数与目标函数呈线性相关，一般单目标问题，其适应度函数可以直接用目标函数f(xi)代替。对于超出时间窗约束之外和超出车辆最大载重量的染色体，可以用惩罚函数P(xi)降低适应性。本文中要求车辆的承载量必须在一定的范围之内，所以只考虑超出时间窗之外的染色体。本文的目标函数时间最小化，其适应度可以表示为eval(xi)=-w1f(xi)+w2P(xi)。其中，w1+w2=1。

STEP4：按由个体适应度值所决定的某个规则，选取将进入下一代的个体，体现优胜劣汰的自然规律；

STEP5：按概率Pc进行交叉，交叉体现有性繁殖的思想；

TEPS6：按概率Pm进行变异，变异体现进化过程中的基因突变的思想；

STEP7：若不满足停止条件，转STEP3，否则转下一步。

STEP8：得到种群中适应度值最佳的染色体。此最优染色体即所求车辆路径问题的最优解。

若完成了预先给定的进化代数，程序停止；若连续若干代后，种群中的最优个体没有任何改进，或者连续若干代后，平均适应度代没有改进，程序停止。这是两种最简单的程序停止的情况。

4 实例验证

A企业是一家以客户定制为主的生产制造企业，客户定制的特征决定了其加工车间的生产模式为多品种小批量的生产模式。该企业规模较小，生产所需的物料都储存在一个仓库中心，共有8个工位负责生产，将上述建立的以配送时间最短为目标函数的模型应用到该企业的生产制造车间，以下是该企业的一组数据，表格1是该企业物料储存仓库到各个工位以及各个工位之间的距离，表格2是各工位的物料需求清单，还包括车辆在物料配送过程中在各工位的服务时间、等待装卸物料的时间和每个工位的时间窗限制。将表中的数据作为输入，规定负责物料配送车辆的最大载重量为70，速度最大不超过50，用Matlab7进行编程，求解上述模型，结果见表3。

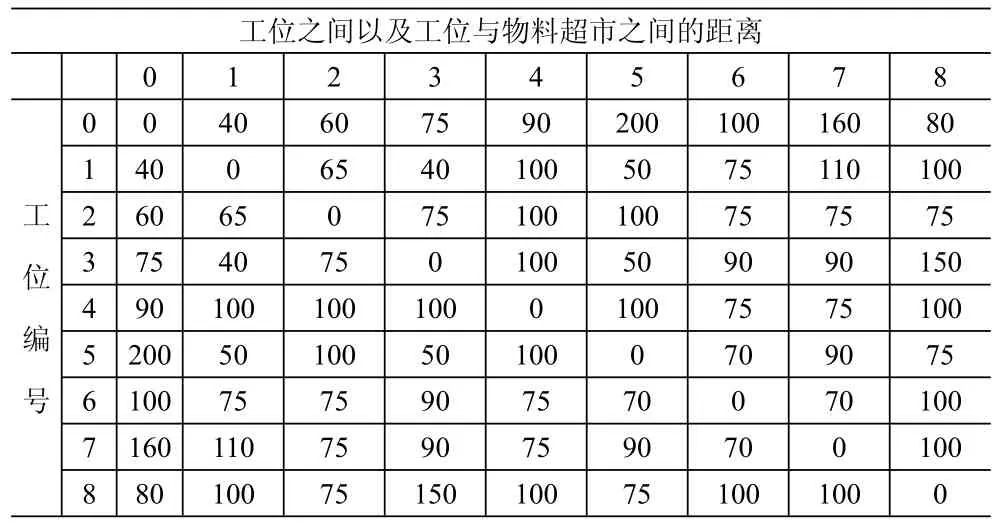
表1 工位之间及工位与物料超市之间的距离

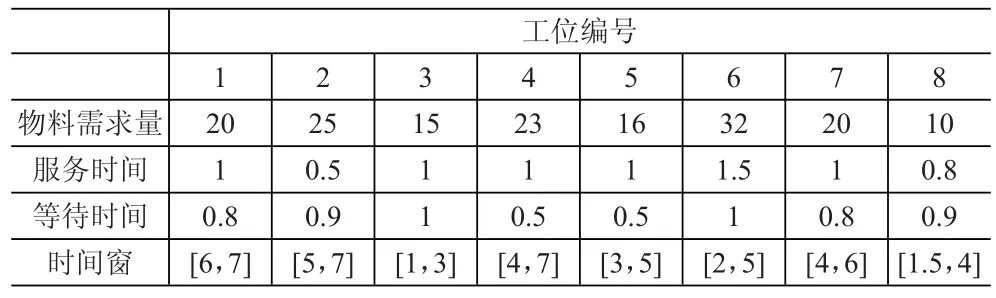
表2 工位物料需求清单

表3 模型求解结果统计

通过以上的赌轮启发式算法用Matab7求解，设置种群的大小为100，运行200代之后算法终止，经过计算，算法在运行10次实验中，平均157代之后表现为收敛，平均运行时间为4.3s，行驶总距离为795。统计实验10次的平均的结果为：

车辆一的物料配送路线是：0—3—5—1—0，满载率为72.9%，完成一次配送的总时间为9.6min；

车辆二的物料配送路线是：0—8—7—2—0，满载率为78.6%，完成一次配送的总时间为11.2min；

车辆三的物料配送路线是：0—6—4—0，满载率为78.6%，完成一次配送的总时间为9.3min。

根据模型求解的结果，画出简易的工位需求的物料配送情况如图1所示。

以上求解的结果可以看出：与企业原始路径相比，优化路径的行驶距离更短，且每条路径的行驶距离都比原来的短；完成一次配送的总时间优化路径最大为11.2，原始的为12.8，两者相比优化路径的时间更短；优化路径中的车辆满载率平均在75%以上，且每辆车都超过70%，原始路径虽然车辆1和车辆2的满载率较高，但车辆3的满载率却偏低，利用率低。因此，与原始路径相比，在使用同样的人力物力的条件下，优化路径所行驶的距离更短，车辆资源消耗更少，花费的时间也更短，更有利于提高企业的生产效率。

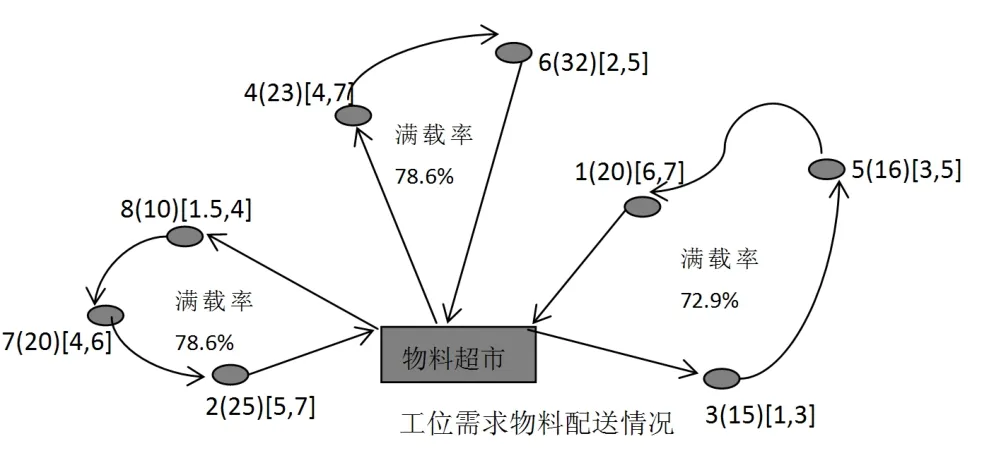
图1 工位需求物料配送情况

5 结论

本文结合多品种小批量生产的特征，在企业制造车间内部工位物料需求时间不确定的基础上，借鉴物流行业现有的车辆路径问题研究，将其应用到车间内部物料配送上，对带有时间窗的车间内部物料配送调度的优化路径展开研究，建立带有时间窗的物料配送路径的数学模型，对于物料到达较时间窗提前或滞后的情况，建立相应的惩罚函数，采用改进的遗传算法求解模型，并将模型应用到一家多品种小批量生产模式的企业案例中，求解出具体的物料配送的路径。将本文提出的模型求解的结果与企业原有的配送路径对比，结果表明本文的模型所用的时间更短，更有助于企业节约时间成本，提高生产效率。车辆满载率虽然不是很高，但平均利用率较高。

[1]李晋航,黄刚,贾艳.多模糊信息条件下的物料配送路径规划问题研究[J].机械工程学报,2011,1(47).

[2]刘明周,王小巧,张铭鑫,等.不确定环境下混流装配线动态准时制物料配送系统[J].计算机集成制造系统,2014,12(20):3 020-3 031.

[3]凌琳,刘明周,葛茂根,等.计及漂移瓶颈的时变物料配送路径优化[J].机械工程学报,2015,51(23):133-143.

[4]Muller J.Approximative solutions to the bicriterion vehicle routing problem with time windows[J].European Journal of Operational Research,2010,202(1):223-231.

[5]王旭坪,张凯,胡祥培.基于模糊时间窗的车辆调度问题研究[J].管理工程学报,2011,(3):148-154.

[6]Banos ttega J,Gll C,et al.A simulated annealing based parallel multi-objective approach to vehicle routing problems with time windows[J].Expert Systems with Application,2013,40(5): 1 696-1 707.

[7]Kilic Sezgin,Kaplan Sezgin.An Efficient Fuzzy Programming Approach for the Vehicle Routing Problem withSoft Time Windows[J].Joutnal of multiple-valued logic and soft computing,2014,4(22):443-457.

[8]章勋宏,贾国柱,孔继利.考虑零件三维装载约束带时间窗的循环取货路径问题研究[J].管理工程学报,2014,(4):207-218.

[9]AndroutsopoulosKonstantinosN,ZografosKonstantinosG. Solving the bicriterion routing and scheduling problem for hazardous materialsdistribution[J].Transportation research part c:emerging technologies,2010,18(5):713-726.

[10]Gao Guibing,Zhang Guojun,Huang Gang.Solving material distribution routing problem in mixed manufacturing systems with a hybrid multi-objective evolutionary algorithm[J]. Journal of central south university,2012,19(2):433-422.

[11]严正峰,梅发东,等.基于模糊软时间窗的车间物料流路径优化方法[J].计算机集成与制造,2015,(10):2 761-2 767.

[12]Simic Dragan,Kovacevic Ilija,Svircevic Vasa.Hybrid Firefly Model in Routing Heterogeneous Fleet of Vehicles in LogisticsDistribution[J].Logic journal of the igpl,2015,23(3):521-532.

Optimization of Workshop Material Dispatching with Soft Time Window

Li Jialing,Qian Wuyong
(School of Business,Jiangnan University,Wuxi 214122,China)

In this paper,based on the concept of the soft time window,we proposed the method for the optimization of the internal dispatching of workshop materials,then upon the given hypotheses,studied the workshop material distribution problem with time window, which aimed at minimizing the total distribution time and established the relevant mathematical model.Next,we solved it using the improved genetic algorithm to obtain the optimal route for the distribution of the workshop materials.At the end,we demonstrated the validity of the model through an empirical study.

material distribution;soft time window;genetic algorithm;dispatching optimization

F252.14;F253

A

1005-152X(2016)12-0135-06

10.3969/j.issn.1005-152X.2016.12.032

2016-10-24

国家自然科学基金项目(71503103)；江苏自然科学基金项目（BK20150157）；江苏省社会科学基金项目（14GLC008）;中央高校基本科研业务费专项资金资助（JUSRP11583;2015JDZD04）

李加玲（1992-），女，江苏南通人，研究生，研究方向：供应链管理；钱吴永（1979-），男，江苏连云港人，副教授，研究生导师，博士，研究方向：系统建模与数量经济。