球谐光照在高度场渲染中的应用
赵克胜+倪桂强+罗健欣
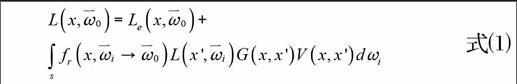


DOI:10.16644/j.cnki.cn33-1094/tp.2016.02.010
摘 要: 为提高高度场渲染的真实感,增加视觉观察的准确性,提出了使用球谐光照渲染高度场的方法。使用OpenGL图形接口进行实验程序开发,采用Puget Sound高度图作为原始数据,利用对比实验说明球谐光照在高度场渲染中对渲染效果、渲染效率的提升。对比结果表明,将球谐光照用于高度场渲染可以有效增强高度场真实感。
关键词: 高度场渲染; 球谐光照; 蒙特卡洛积分; 关联勒让德多项式
中图分类号:TP391.41 文献标志码:A 文章编号:1006-8228(2016)02-33-05
Terrains rendering with spherical harmonic lighting
Zhao Kesheng, Ni Guiqiang, Luo Jianxin
(Laboratory of Military Network Technology, PLA University of Science and Technology, Nanjing, Jiangsu 21007, China)
Abstract: In order to improve the sense of reality of terrains rendering and the accuracy of visual observation, a method of rendering terrains with spherical harmonic lighting is proposed. In the experiment, the OpenGL graphics interface is used as the development environment and the Puget Sound terrains as the raw data. The advantage of terrains rendering with spherical harmonic lighting in rendering quality and efficiency is described by the comparative experiment. The result shows that spherical harmonic lighting can improve the rendering quality of terrains rendering.
Key words: terrains rendering; spherical harmonic lighting; Monte-Carlo integration; associated Legendre polynomials
0 引言
近年来球谐(Spherical Harmonic)在光照、BRDF、形状识别等计算机图形学领域内被广泛使用[1]。球谐光照[2-5]是利用球谐计算3D模型上光照的技术,它可以实时地渲染出全局光照模式的图像[6]。相对于光线追踪[7]、辐射度算法[8]等光照技术,球谐光照具有渲染效果好、实时性强、代码易编写等优点。
高度场渲染在模拟飞行、虚拟战场三维游戏等领域都有着广泛应用[9]。通过对高度场场景模型加入光照效果将会大大增强结果图像的真实感[10],为交互可视化和视觉观察提供很大的便利。由于高度场本质上也是3D模型,所以本文研究了将球谐光照应用于高度场渲染,并对其优缺点进行了分析。
1 球谐光照
1.1 光照计算
图1所示为自然界中的某个光照场景,光线自左侧传播至x处,经物体反射至x'处。此时观察者于x'观察到的x点的颜色由两部分组成:一部分为x点本身发射出的沿xx'方向的光的颜色,另一部分为入射光线于x处经物体反射至x'处的光的颜色。在计算机图形学中,模拟这种物理现象的公式称为渲染方程[11]:
式⑴
其中是观察者在方向看到的x点的颜色。是物体在x点沿着方向自身发射的光的颜色。将沿的入射光颜色转化为沿方向的反射光颜色。L(x',)是从x'点发射沿方向的入射光,G(x,x')是x与x'的几何关系。V(x,x')是x点对x'点的可见测试。
<E:\方正创艺5.1\Fit201601\图\zks图1.tif>
图1 自然界中的光照场景
可以看出,使用图形硬件来计算的难点在于,渲染公式中存在一个球上的积分,计算基于符号的积分在GPU中很难完成。为了能快速地得到结果,人们使用了一个近似的解法,这个方法就是球谐投影与重建。球谐投影与重建的原理是,使用球谐函数求原函数的近似解。球谐函数是一类拥有特殊性质的基函数。
1.2 基函数
基函数是用来求解原函数近似解的一系列函数。利用基函数求原函数近似解的过程如下:
首先在原函数的定义域上积分原函数f(x)i与基函数Bi(x)的乘积,得到一系列的近似系数Ci,如图2。
然后用系数Ci乘以各自对应的基函数Bi(x),如图3。
最后将乘积结果累加,得到原函数的近似结果,如图4。
1.3 关联勒让德多项式
球谐函数的核心部分是关联勒让德多项式,关联勒让德多项式是标准正交多项式的一族。标准正交多项式是拥有以下的性质的一组基函数:积分任何两个正交基函数的积时,如果它们相同,结果为1,如果它们不同,结果为0即:
式⑵
关联勒让德多项式通常使用符号P表示,关联勒让德多项式有两个参数:l和m。l的定义域为从0开始的整数,m的定义域为0到l的整数。系数l和m把关联勒让德多项式分成了不同的阶,l是阶的索引,同一阶内的多项式正交于同一个常数,不同阶内的多项式正交于不同的常数。这种关系可以用如图5中的三角网格来表示:
图5 三角网格
我们使用递归定义来求解给定参数的关联勒让德多项式,这个过程需要用到下面三个公式。
式⑶
首先使用这个式子和给定的m求解出,注意x!!为双阶乘运算,其结果为所有小于等于x并与x有相同奇偶性的整数的乘积,例如5!!=5*3*1=15。如果此时l=m,就终止程序,如果l≠m则使用公式⑶来求:
式⑷
上一步由公式⑵求得的代入此式,即可求得。此式只使用一次,若此时m+1=l,则终止程序,如果m+1≠1则使用公式4递归求解:
式⑸
1.4 球谐函数
在球面上,我们使用球谐函数来求原函数的近似解。与关联勒让德多项式相似,球谐函数也拥有两个参数l和m。l将球谐函数分为了不同的阶,它的取值范围从0开始的整数,与关联勒让德多项式不同的是球谐函数的参数m的取值范围为-l到l的整数。球谐函数通常用符号y来表示,它的定义如下:
式⑹
P为关联勒让德多项式,K是比例因子:
式⑺
定义顺序yi如下:
式⑻
1.5 球谐投影
观察渲染方程发现,G(x,x')和V(x,x')均为常数,则渲染方程中积分的实际形式为,它的求解过程如下。使用球谐函数来近似L(s)和t(s),方法与使用基函数求原函数近似的过程相同。
用和来代替L(s)和t(s):
展开:
继续展开:
由于球谐函数是正交多项式的子族,所以拥有以下性质:
故有:
其中:
求解这两个定积分的方法是蒙特卡洛积分。
1.6 蒙特卡洛积分
在实际中,许多需要计算多重积分的复杂问题,使用蒙特卡洛积分[12-14]都能有效地解决。它的推导过程如下。
已知函数f(x)的期望等于函数本身f(x)与它的概率密度函数p(x)的乘积在函数f(x)定义域上的积:
另一个计算函数期望的方法是,取大量的函数随机采样的平均值,若采样数趋于无穷大,则最终结果收敛于函数期望:
所以,由此可推得:
将上式两侧都除以p(x),得到蒙特卡洛积分:
式⑼
通过这种转换,一个函数的积分运算就转化成了四则运算,在计算机中可以方便地求得结果。
运用蒙特卡洛积分方法求解1.5节中的积分得:
由于渲染方程需要解决的是一个球面上的积分,所以利用蒙特卡洛积分求解渲染方程时需要在整个球面上随机采样离散分布的点。可以采用某种策略先得到2D的采样点,然后将其映射到球面空间上。映射的公式如下:
式⑽
如图6所示,类似于将平面的世界地图贴到地球仪上,为了保证映射后的采样点随机且均匀,需要注意到采样点在2D坐标下的分布规律为沿两极向赤道越来越密集。具体的采样方法是创建一个1*1的采样空间,划分成N*N的网格,每个网格内取一个坐标,用公式⑽将其转化为球坐标,再利用公式⑸求得每个采样点对应的球谐函数值。
因为是在单位球上均匀分布的采样点,所以。因此有:
这样利用球谐投影与重建求解3D模型上某一点经过光照后颜色的整个过程就结束了。
2 利用球谐渲染高度场
2.1 实验准备
实验硬件平台为Intel(R) Core(TM) i5-4460 CPU @ 3.20GHz、8GB内存,Radeon X1300/X1550 Seris显卡的PC,采用VC++作为开发语言,VS2012作为开发平台。实验数据来源于Puget Sound数据集,为1025*1025分辨率的原始高程数据。
2.2 同一四叉树映射
高度场渲染常用四叉树作为数据管理方式。现有的四叉树结构渲染节点的过程需要对节点关联的网格进行简化并将简化后的网格发送到GPU上。由于四叉树节点关联的网格三角形数目巨大,所以这一过程往往会限制渲染效率。
通过采用同一四叉树映射[15]的方法可以有效提高渲染效率。同一四叉树映射基于GPU支持顶点可编程性、强大的处理能力等特点。将统一的均匀网格驻留在GPU中,在渲染四叉树节点时,通过简单的顶点着色将网格顶点移动到指定位置进行渲染。这样做虽然增加了三角形数量,但是因为完全丢弃了网格简化及将网格数据发送到GPU中的过程,所以反而提高了渲染效率。
2.3 渲染结果
图7为无阴影的球谐光照渲染的高度场图片,图8为相同渲染场景的对比实验效果。对比画框处,球谐光照的阴影效果更好,更易于分辨地形的起伏变化。
图9为球谐光照渲染的高度场的平视图,图10为相同场景的对比实验效果。对比画框处,球谐光照背光处的立体感很真实,视觉观察的准确性更高。
图11为球谐光照渲染的草地场景,图12为相同渲染场景的对比实验效果。可以看出,球谐光照把草地阴影的效果渲染得很好。
3 结束语
实验结果表明,将球谐光照用于高度场的渲染能有效提升高度场图片的真实感,为使用者的视觉观察与可视化交互增加准确性。球谐光照用于高度场的缺点在于,球谐光照的预处理时间随着网格节点的增长呈O(n2)的增长趋势,所以,如何有效简化网格成为下一步研究的重点。
参考文献(References):
[1] Lisle, Ian & Huang, Tracy(2007).Algorithms for spherical
harmonic lighting[R]. GRAPHITE 2007: Proceedings of the 5th International Conference on Computer Graphics and Interactive Techniques in Australia and Southeast Asia,2007.12:1-4
[2] P.P.Sloan,J.Kautz,and J.Snyder,"Precomputed radiance
transfer for real-time rendering in dynamic,low-frequency lighting environments"[J].in SIGGRAPHPH' 02:Proceedings of the 29th annual conference on computer graphics and interactive techniques.New York,NY,USA:ACM Press,2002:527-536
[3] X.Liu, P.Sloan, H-Y.Shum, J.Synder. All-frequency
precomputed radiance transfer for glossy objects[J].Proc of Eurograhis Symposium on Rendering'04,2004:337-344
[4] P.Sloan, J.Hall, J.Hart, J.Synder. Clustered principal
components for precomputed radiance transfer[J].Proc.OF SIGGRAPH'03,2003:382-391
[5] Sloan P, Liu X, Shum H, et al. Bi-scale radiance transfer[R].
ACM-Transactions onGraphics, 2003.22(3):370-375
[6] Robin Green,Spherical Harmonic Lighting: The Gritty
Details.
[7] Whitted J.T.,An Improved Illumination model for shaded
display[J],CACM,1980.23:343-349
[8] Shirley P, A Ray Tracing Method For Illumination
Calculation In Diffuse-specular Scense[J]. In:Proc of CG International'90, New York,1990:469-476
[9] 刘思江,翁璐斌,秦树鑫,杨一平,蒋永实.保持边界到的地形
网格简化算法与组织格式[R].计算机辅助设计与图形学学报,2013.25(1).
[10] Luo JX,Ni G Q,Cui P,et al. Quad-tree atlas ray casting:a
gpu based frameword for terrain visualization and its applications [M].Lectrue Notes in Computer Science. Heidelberg:Springer,2012,7145:74-85
[11] Kajiya,J.The Rending Equation[J]. SIGGRAPH' 86,
143-150
[12] L.Szirmay-Kalos, Monte-carlo global Illumination
Methods-State of the Art and New Developments[R].Budimerce, Slovakia:Comenius University,1999:3-21
[13] Wald I, Realtime Ray Tracing and Interactive Global
Illmination[D]. Phd thesis, Saarland University,2004.
[14] L.Szormay-Kalos. Monte-carlo global illumination
methods-state of the art and new developments[R]. In proceedings of the Fifteenth Spring Confernce on Computer Graphics. Budimerce, Slovakia:Comenius University,1999:3-21
[15] 罗健欣,胡谷雨,倪桂强.平行流形空间光线投射高度场可
视化算法[J].计算机辅助设计与图形学学报,2013.25(3).

