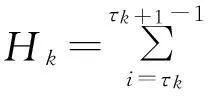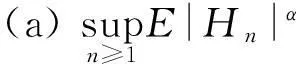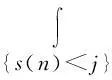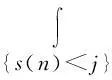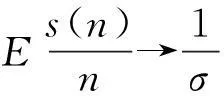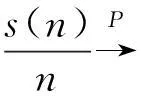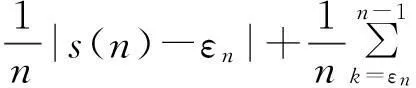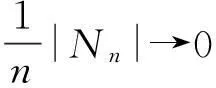绕积马氏链函数的强大数定律

黄敏,黄朝炎

(1.武汉学院信息系,湖北 武汉 430200; 2.湖北大学数学与统计学学院,湖北 武汉 430062)



绕积马氏链函数的强大数定律

黄敏1,黄朝炎2

(1.武汉学院信息系,湖北 武汉 430200; 2.湖北大学数学与统计学学院,湖北 武汉 430062)

摘要：主要研究绕积马氏链函数的强大数定律,得到绕积马氏链函数强大数定律成立的充分条件.

关键词：随机环境;绕积马氏链;强大数定律

20世纪80年代初,Cogburn R等人开始研究随机环境中马氏链的一般理论,取得了 一系列深刻的结果[1-3].Orey S[4]在Cogburn R等人的研究基础上对随机环境中马氏链进行了深入的研究,并提出了一系列的问题,引起了众多概率论学者的广泛关注,使得随机环境中马氏链一般理论的研究成为国际上又一新的研究方向.国内学者对这一领域进行了深入的研究[5-8].大家知道,随机变量序列的强大数定律的研究一直是经典极限理论研究中的热门课题,取得的结果已十分深入.这种研究不仅仅是受到大数定律研究的推动,而且在考虑线性模型最小二乘估计的相容性时就要讨论随机变量序列的强大数定律,因此这种研究无疑是非常重要的.笔者研究了绕积马氏链函数的强大数定律,得到了绕积马氏链函数强大数定律成立的充分条件.

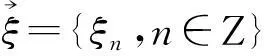
如果对任意A∈A,n≥0有

(1)

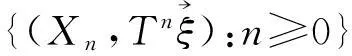
对k≥0, 当τk

引理1{Hk,k≥0}是(Ω,F,P)上的相互独立的随机变量序列.

由强马氏性知

P(H0=a0,…,Hk=ak)=

P(H0=a0,…,Hk-1=ak-1)P(Hk=ak),

于是由数学归纳法可知引理1的结论成立.

推论2对任意的实数a,b,{aHk+bσk,k≥0}是(Ω,F,P)上的相互独立的随机变量序列.

特别地{σk,k≥0}是(Ω,F,P)上的相互独立的随机变量序列.

定理1如果下述条件成立:

则有

(2)

首先证明

(3)

由于{s(n)

从而

(4)

由条件(b)知

令

(5)

(6)

因此,对任意的ω∈Ω0及ε>0, 存在N1(ω)>0,使当n≥N1(ω)时有

(7)

P(s(n)≥εn)<ε

(8)

(9)

(10)

(11)

由(7)式知,对任意的ω∈Ω0,存在N3(ω)≥max{N1(ω),N2(ω)},使当n≥N3(ω)时有

(12)

由(8)、(9)式知,对任意的ω∈Ω0,存在N4(ω)≥N3(ω),使当n≥N4(ω)时有

(13)

由ε,δ的任意性及(12-13)式知,对a.s.ω, 当n→∞时,(10)式的第1, 2项趋于0, 从而(3)式成立.

若σ=1, 由(6)式知

类似地可以证明(3)式成立.

(14)

最后由条件(a)及推论2知

从而

两式相减,应用条件(a)有

(15)

类似地有

(16)

由(14-16)式、(2-3)式及知定理3的结论成立.

参考文献

[1] Cogburn R. The ergodic theory of Marköv chains in random environments[J].Z.Wahrsch Verw Gebiete, 1993,66(2): 109-128.

[2] Cogburn R. Marköv chains in random environments: the case of Markovian environment[J]. Ann Prob, 1980,8(3): 908-916.

[3] Cogburn R. On the central limit theorem for Marköv chains in random environments[J]. Ann Prob,1991,19(2): 587-604.

[4] Orey S. Markov chains with stochastically stationary transition probabilities[J]. Ann Prob, 1999,19(4): 907-928.

[5] 王汉兴,戴永隆. 马氏环境中马氏链的Poisson极限律[J]. 数学学报,1997,40(2): 265-270.

[6] 方大凡.马氏环境中马氏链的Shannon-McMillan-Breiman定理[J].应用概率统计,2000,16(3): 295-298.

[7] 李应求.双无限随机环境中Marköv链的常返性与不变测度[J].中国科学(A辑),2001,31(8):702-707.

[8] 郭明乐. 双无限随机环境中马氏链的强大数定律[J].应用数学,2005,18(1): 174-180.

[9] 严加安.测度论讲义[M].北京:科学出版社,1998.

(责任编辑赵燕)

The strong law of large numbers for function of skew product Marköv chains

HUANG Min1, HUANG Chaoyan2

(1.Faculty of Information,Wuhan College,Wuhan 430200,China;

2.Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062,China)

Abstract:We studied a strong law of large numbers for function of skew product Marköv chains, and obtained a sufficient condition for the strong law of large numbers.

Key words:random environments; skew product Marköv chains; strong law of large numbers

中图分类号:O211.62

文献标志码:ADOI:10.3969/j.issn.1000-2375.2016.01.003

文章编号:1000-2375(2016)01-0014-04

作者简介:黄敏(1985-)，女，硕士，讲师，E-mail:253301841@qq.com

收稿日期:2015-06-18