电力系统负荷节点在线电压稳定指标研究

高峰, 王彦文，郭林，徐睿

(1.中国矿业大学(北京)，北京市 100083；2.国网山东省电力公司德州供电公司，山东省德州市 253000)

电力系统负荷节点在线电压稳定指标研究

高峰1, 王彦文1，郭林1，徐睿2

(1.中国矿业大学(北京)，北京市 100083；2.国网山东省电力公司德州供电公司，山东省德州市 253000)

利用同步相量测量单元(phasor measurement unit，PMU)测得任意(非PV)节点及其相邻母线的电压、线路潮流等实时数据，建立一种新的网络等值模型。同时，基于该模型提出了综合考虑负荷节点有功功率和无功功率的在线电压稳定指标；提出在线电压稳定有功功率指标和在线电压稳定无功功率指标分别用作表征负荷节点的有功功率裕度和无功功率裕度，作为对节点(系统)在线电压稳定指标的补充。如果负荷节点在线电压稳定指标值接近临界值1，则表明系统临近电压崩溃。EPRI-36节点仿真分析表明该方法可有效判断系统电压稳定性，适用于在线电压稳定监测和预估。与其他指标的对比结果体现了本文模型和指标的合理性与优越性。最后通过对山东电网500 kV主网负荷节点电压稳定裕度评估简要说明本文所提方法的可行性。

电压稳定；在线电压稳定指标；同步相量测量单元(PMU)；网络等值模型

0 引 言

近年来世界范围内发生了多起大停电事故，给社会和经济带来了巨大的损失。停电事故的原因是多方面的，但最终主要表现为电压失稳和电压崩溃[1-4]。为了预防电压失稳和电压崩溃，系统电压稳定裕度，即当前电力系统运行状态离崩溃点的距离，成为电力调度工作人员最关心的问题。因此，制定一个准确衡量电压稳定程度的指标，对于有效体现电压稳定裕度，预警电压失稳和电压崩溃至关重要。现有的静态电压稳定性指标主要有灵敏度指标[5-6]、最小特征值(奇异值)指标[7]、试验函数指标[8]、负荷裕度指标[9-10]、L指标[11]等。但这些指标普遍存在计算量大、准确性低、线性度差的问题，都不能在线预警电压失稳[12-13]。

为了实用、简捷地快速判断系统的电压稳定裕度，基于上述静态电压稳定性指标，许多新的电压稳定指标已被提出。文献[14]提出的算法关键在于求取电网络戴维南等效参数，并假设等效参数在2个或多个系统状态间是不变的，计算误差较大；文献[15]基于雅可比矩阵，从负载母线临界电压崩溃点的电压相角和无功损耗特征，推导出的指标算法不适用于电压稳定的在线监测；文献[16]提出了一种利用母线电气参数求取电压稳定裕度的新算法，其算法精度严重依赖于母线电气参数的连续求取；文献[17]提出一种新的L指标，但该推导方法采用的线路模型忽略了支路对地电容的影响，不适用于高压大电网系统；文献[18]采用的П型线路模型虽然考虑了支路对地电容，但未考虑系统对被测线路的影响，结果误差较大；文献[19]提出的电压稳定指标建立在等值电压源和等效负荷功率因数不变的基础上，指标无法跟踪体现系统影响下的节点电压变化。

针对以上问题，本文提出一种新的电力系统在线电压稳定指标。该指标基于同步相量测量单元(phasor measurement unit，PMU)测得的实时数据，建立被测负荷节点的相关支路网络等值模型，考虑相关支路对被测线路的影响。同时，相对于求取网络戴维南等效参数，需要求取的等值阻抗只是该模型阻抗的一部分，减小了网络等值模型误差，提高了模型的准确度。更重要的是，新指标综合考虑负荷节点的有功功率和无功功率极限裕度，能适用于线路传输功率因数和负荷节点功率因数变化的情况；能在系统发生电压崩溃时接近于1，且具有较高的精度和线性度；能直接估算出节点负荷的电压稳定裕度，无须计算系统潮流；计算速度快，便于在线实用。

1 静态电压稳定分析模型

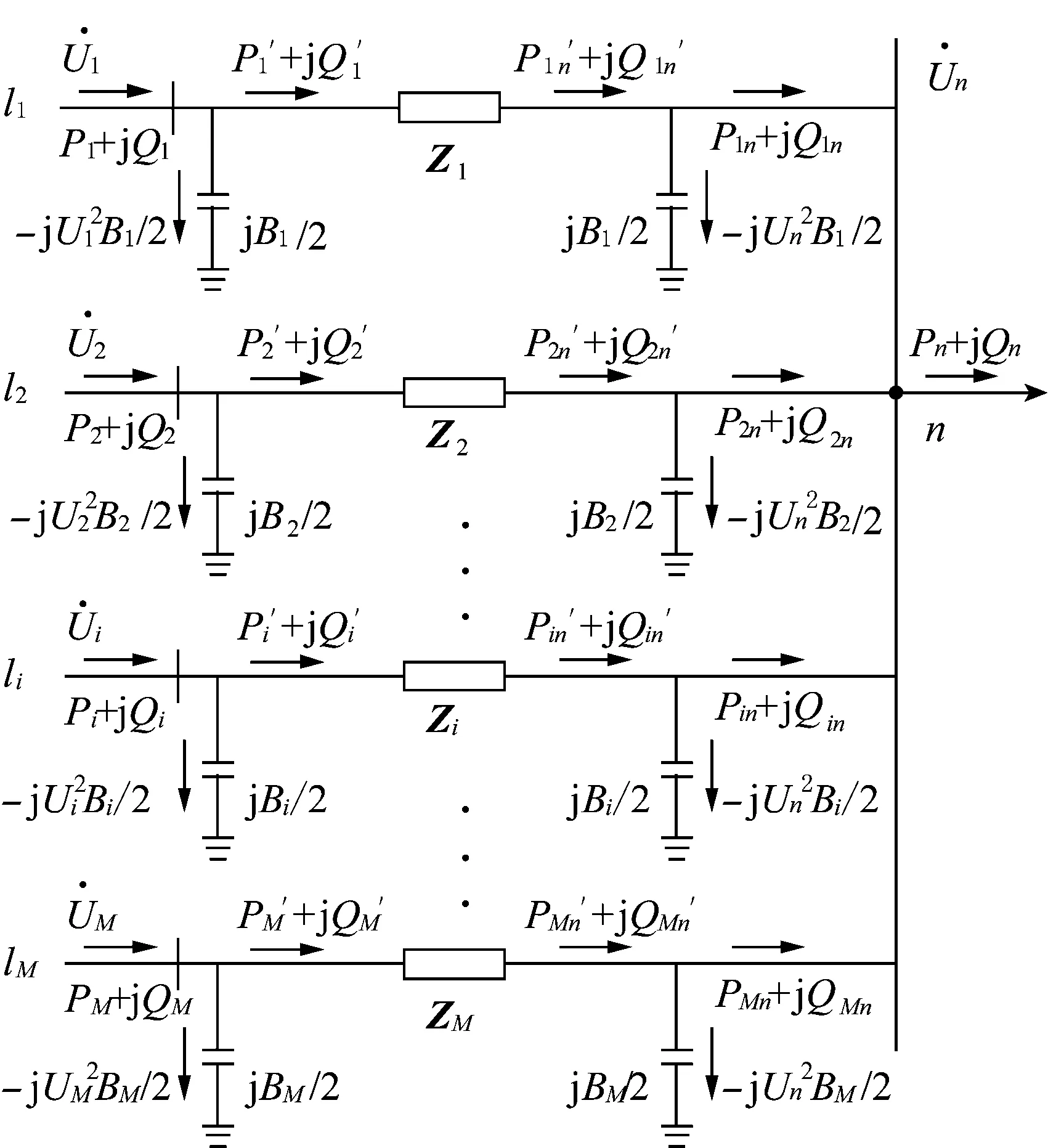
图1 被测节点及其相连线路Fig.1 Measured node with network around

图2 被测节点及其相连线路等值模型Fig.2 Equivalent model of measured node with network around

2 在线电压稳定指标

(1)

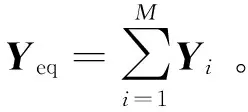
(2)

分解Pn、Qn得：

(3)

(4)

式中δ=δeq-δn。将Yeq= 1/Zeq代入式(3)、式(4)可分别得：

(5)

ZeqQn=0

(6)

2.1 在线电压稳定指标

(7)

由式(7)可知，为保证Un有2个正实根，要求其判别式大于等于0，即

(8)

式(8)等价于

(9)

将节点在线电压稳定指标(on-linevoltagestabilityindex)定义为

(10)

整个系统的在线电压稳定指标定义为

(11)

式中：LnVSI为时间断面t时，节点n的电压稳定指标；S代表系统的节点集。用LnVSI的最大值LsVSI表征系统的电压稳定指标，系统首先在这里发生电压崩溃。LsVSI的值越接近1，则节点(系统)越接近电压崩溃点。

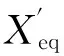
式(11)是考虑了负荷节点有功功率Pn和无功功率Qn而提出的电压稳定指标，体现了负荷节点在(P，Q，U)空间曲面[20]上运行时，对曲面临界点的接

近程度。但是，式(11)仅能反映负荷节点电压稳定的“综合指标”，无法分别体现负荷节点的有功功率和无功功率裕度。

而PV曲线是负荷节点Pn、Qn、Un三者关系曲面(属于(P，Q，U)空间)在(P，U)平面上的投影，反映了一定PQ关系下(比如一定功率因数)，节点的有功功率裕度；VQ曲线是曲面在(U，Q)平面上的投影，反映了P值一定时，节点的无功功率裕度[20-22]。由此，本文在前述等值模型的基础上，利用文献[18]和文献[23]所提的电压稳定判据提出电压稳定有功功率指标和无功功率指标，作为对式(10)和式(11)的补充，也作为与本文所提指标的对比。

2.2 在线电压稳定有功功率指标

当式(5)的根判别式大于等于0时，即

(12)

式(5)有2个实数解：

(13)

假设0 <θeq-δ< 90°(一般情况下该命题亦是成立的)，且0 <θeq< 90°，为保证式(5)有2个正实根，式(12)成立即可。式(12)等价于

(14)

将式(14)定义为节点n的在线电压稳定有功功率指标(on-linevoltagestabilityindexofactivepower)[18]，即

(15)

式中LnVSIP表征节点n在时间断面t时，在PV曲线上对曲线拐点的接近程度，反映节点的有功功率裕度。LnVSIP的值越接近1，则节点越接近电压崩溃点(有功功率负荷能力极限)。

2.3 在线电压稳定无功功率指标

当式(6)的根判别式大于等于0时，即

ΔQn=[Ueqsin(θeq-δ)]2-

4QnZeq(sinθeq-ZeqBeq/2)≥0

(16)

式(6)有2个实数解：

(17)

而0 <θeq-δ< 90°，0 <θeq< 90°，sinθeq≥ZeqBeq/2。为保证式(6)有2个正实根，式(16)成立即可。式(16)等价于

(18)

将式(18)定义为节点n的在线电压稳定无功功

率指标(on-linevoltagestabilityindexofreactivepower)[23]，即

(19)

式中LnVSIQ表征节点n在时间断面t时，在VQ曲线上对曲线拐点的接近程度，反映节点的无功功率裕度。LnVSIQ的值越接近1，则节点越接近电压崩溃点(无功功率负荷能力极限)。

具有LnVSIP最大值的负荷节点，表示该节点是系统内有功功率裕度最小的负荷节点；具有LnVSIQ最大值的负荷节点，表示该节点是系统内无功功率裕度最小的负荷节点；具有LnVSI最大值的负荷节点，则表示该节点电压稳定裕度最小，最有可能引起整个系统的电压崩溃。

3 仿真结果与分析

本文以WEPRI-36系统为例，采用综合电力系统分析综合程序(power system analysis software package，PSASP)进行数值仿真。本文首先以2种负荷波动形式进行仿真分析：(1)所有节点负荷以初始功率的10%增加，主要通过该负荷增加方式分析系统最弱支路；(2)单独增加某一节点负荷(增加量保持恒功率因数)，主要通过该负荷增加方式分析负荷节点间的相互影响。最后与其他指标进行对比，并利用本文所提指标对山东电网500 kV主网负荷节点进行电压稳定裕度评估。

3.1 所有节点负荷以初始功率的10%增加

系统在原负荷的基础上，各节点负荷以初始功率的10%增加(保持负荷原功率因数不变)，直到系统临近电压崩溃。PSASP中，采用这种负荷增加方式，系统发生电压崩溃时，不仅负荷节点的功率增加倍数相同，而且某个负荷节点有功功率增加倍数和无功功率增加倍数也相同。

本文对具有代表性的负荷节点9、16、18、20、21和29的电压稳定性进行判断分析。

(1)LnVSI曲线分析

综合考虑节点有功功率和无功功率，判断负荷节点电压稳定裕度。图3为系统电压崩溃前节点LnVSI曲线图。

从图3中可以看出，随着功率的增加，L20VSI到达最大值0.997 6 pu，较其他LnVSI首先接近于临界值1，据此判定是节点20发生电压失稳导致系统电压崩溃。从图3中可以看出，最弱负荷节点(综合考虑节点有功功率和无功功率时，电压稳定裕度最低的负荷节点)从节点21转移到了节点20，直至系统电压崩溃。

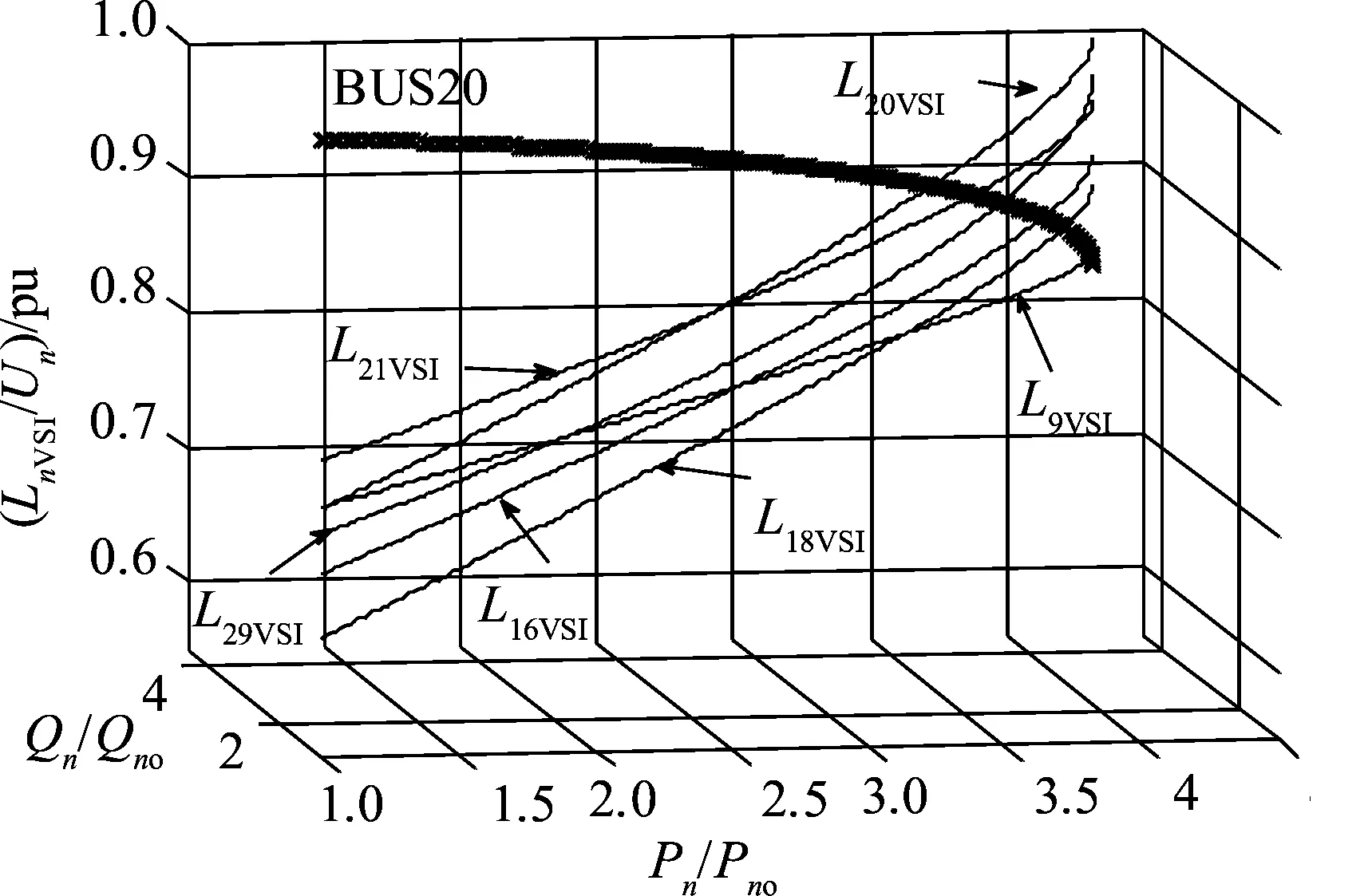
图3 各负荷节点以其初始值的10%增加时的 电压稳定指标Fig.3 Each load node and voltage stability index with load increasing by 10% of initial value

(2)LnVSIP和LnVSIQ分析

系统各负荷节点以其初始功率的10%增加，负荷节点电压Un随其无功功率Qn与初始无功功率Qno的比值变化曲线(Un-Qn/Qno曲线)与Un-Pn/Pno曲线相同，只是横坐标代表Qn/Qno，这里仅以Un-Pn/Pno曲线为例说明。但是节点LnVSIQ曲线和LnVSIP曲线是不同的，后文将进行分析说明。

图4为负荷节点电压Un随其有功功率Pn与初始有功功率Pno的比值变化曲线(Un-Pn/Pno曲线)。从图4可以看出，BUS16一直保持着较高的电压水平，这是因为BUS16连接并联电容器，具有充足的无功功率，同时BUS16和6条支路相连接，是连接支路最多的节点，能够很好地得到周边节点的功率/电压支撑。BUS16的电压落差值(初始电压幅值与电压崩溃时刻的电压幅值之差)是最小的，但电压稳定指标L16VSI并不是最大的(见图3)；BUS9的电压落差值最大，但其电压稳定指标L9VSI也不总是最小的(见图3中L9VSI前半段)。这说明不能简单地以负荷节点电压降落大小来判断系统电压稳定水平。

图5为负荷节点在系统电压崩溃前的电压稳定有功功率指标变化曲线。随着负荷节点有功功率的增加(Pn/Pno值增大)，负荷节点20的LnVSIP曲线L20VSIP达到最大值0.976 1 pu，较其他LnVSIP首先接近于临界值1。图5中节点20和节点21的电压稳定有功功率指标曲线L20VSIP和L21VSIP的交点，与图4中其Un-Pn/Pno曲线BUS20和BUS21的交点很明显并不在同一时刻(相同的Pn/Pno值)。这说明不能以有功功率、电压幅值是否相同来判断2个负荷节点是否具有相同的电压稳定有功功率裕度。

负荷节点在系统电压崩溃前的电压稳定无功功率指标变化曲线如图6所示。从图中可以看出，随着负荷节点无功功率的增加(Qn/Qno值增大)，负荷节点29的LnVSIQ曲线L29VSIQ达到最大值0.968 9 pu，较其他LnVSIQ首先接近于临界值1。需要注意的是：在图5中节点29的电压稳定有功功率指标L29VSIP比较低，但图6中节点29的电压稳定无功功率指标L29VSIQ不但初始值较高，而且最终发展为系统最大值。可见，同一负荷节点对有功功率和无功功率的敏感程度是不一样的，需要对节点的有功功率裕度和无功功率裕度区别对待。

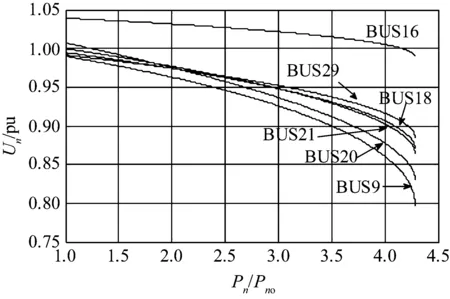
图4 各负荷节点以其初始值的10%增加时的 电压值(有功功率部分)Fig.4 Each load node and voltage (of active power) with load increasing by 10% of initial value

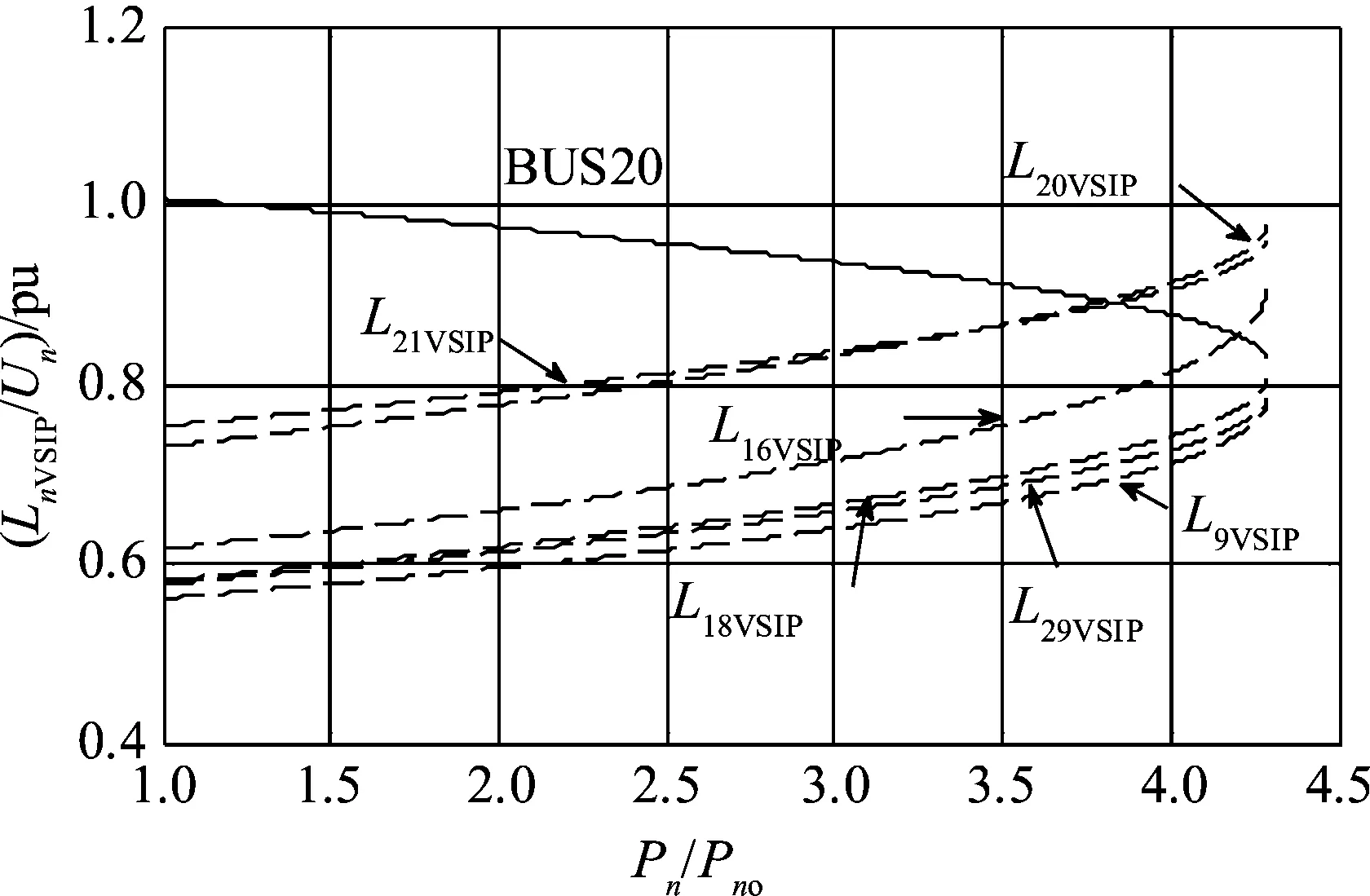
图5 各负荷节点以其初始值的10%增加时的 电压稳定有功功率指标Fig.5 Each load node and voltage stability index of active power with load increasing by 10% of initial value

(3)综合分析

1)Un-Pn/Pno(和Un-Qn/Qno)曲线位置和变化趋势十分接近的负荷节点，其电压稳定指标曲线，包括LnVSI、LnVSIP和LnVSIQ，可能相差较大(如图4中的BUS18和BUS21图形十分相似且位置接近，但是图3、图5、图6中的两者的指标曲线都相差较大)。这是因为负荷节点各自周边网络线路及其负载情况不同，导致节点电压崩溃点、电压稳定指标曲线走势等会有较大差别。采用网络等效模型，计及被测负荷节点周边线路的影响体现于此。

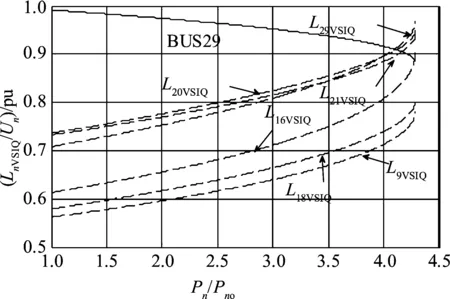
图6 各负荷节点以其初始值的10%增加时的 电压稳定无功功率指标Fig.6 Each load node and voltage stability index of reactive power with load increasing by 10% of initial value

2)在图5中，随着有功功率的增加，L20VSIP首先达到电压崩溃点；而在图6中，随着无功功率的增加，L29VSIQ首先达到电压崩溃点。

3)以电压稳定有功功率指标判断系统最弱支路情况是从节点21向节点20转移，如图5所示；而以电压稳定无功功率指标判断系统最弱支路情况是节点20向节点29转移，如图6所示。

系统通过不同的功率指标(有功功率指标或无功功率指标)得出不同的最弱节点和不同的电压稳定裕度值。这是因为负荷节点的Un-Pn/Pno和LnVSIP曲线(或Un-Qn/Qno和LnVSIQ曲线)只是从有功功率(或无功功率)侧面体现节点的功率极限和裕度，没有综合考虑有功功率和无功功率同时影响。因此，如文献[18]、[24]和[25]等仅仅依靠有功功率或者无功功率作出的电压稳定指标来判断系统的电压稳定裕度是不准确的，甚至是矛盾的。这为本文判据式(10)的提出提供了实验依据。

3.2 恒功率因数增加节点负荷

以0.95的恒功率因数逐渐增加节点21的负荷，其他节点的负荷保持不变，直到系统临近电压崩溃。

(1)LnVSI曲线分析

图7为系统电压崩溃前节点在线电压稳定指标曲线图。图7中可以看出，随着节点21负荷功率的增加，LnVSI到达最大值(0.995 0 pu)，较其他LnVSI首先接近于临界值1，据此判定是节点21发生电压失稳导致系统电压崩溃。

在临近电压崩溃时，L16VSI快速上升且具有较大值，最终仅次于L21VSI，而在图3中，L16VSI一直保持较低值。节点16与无功功率补偿器相连并且连接6条支路，可以说是负荷节点中可以获得来自周边节点的功率/电压支撑最多的节点，但是因受节点21牵连，电压稳定裕度仍旧急速减少。可见，一旦某一负荷节点发生电压失稳，则会大大降低附近节点(特别是为系统提供无功功率输出的节点)的电压稳定裕度，并波及附近区域乃至整个网络。

图7 以恒功率因数0.95增加节点21负荷时的电压稳定指标Fig.7 Voltage stability index with the 21st bus’s load increasing by the power factor 0.95

(2)LnVSIP和LnVSIQ分析

图8为负荷节点电压Un随节点21负荷有功功率P21与其初始有功功率P21o的比值变化曲线(Un-P21/P21o曲线)。图9为负荷节点电压Un随节点21负荷无功功率Q21与其初始无功功率Q21o的比值变化曲线(Un-Q21/Q21o曲线)。从图8、图9看出，系统节点的Un-P21/P21o曲线和Un-Q21/Q21o曲线十分相似，仅仅是横坐标最大值不一样，即节点有功功率和无功功率的增加倍数不一样。

对比图4和图8、图9可以发现：BUS9的电压跌落幅值明显减小；BUS29和BUS18的交点后移；各节点在临近电压崩溃点处的电压幅值也发生不同变化。

图8 以恒功率因数0.95增加节点21负荷时的 电压值(有功功率部分)Fig.8 Bus voltage against the 21st bus’s load increasing by the power factor 0.95 (active part)

图9 以恒功率因数0.95增加节点21 负荷时的电压值(无功功率部分)Fig.9 Bus voltage against the 21st bus’s load increasing by the power factor 0.95 (reactive part)

这说明不同的负荷增加方式对整个系统电压的影响是不同的，负荷节点的电压稳定裕度模型需要从整个网络的层面去考虑。

图10和图11分别为负荷节点在系统电压崩溃前的电压稳定有功功率指标和无功功率指标。随着节点21负荷有功功率和无功功率的增加(P21/P21o和Q21/Q21o值增大)，负荷节点21的电压稳定指标值L21VSIP和L21VSIQ较其他节点指标值首先接近于临界值1。与图6中的L29VSIQ不同，图11中L29VSIQ没有随负荷的增加快速上升而超过其他曲线，这是因为负荷增加的节点21离节点29较远，还不足以引起L29VSIQ超过L21VSIQ。但是，可以明显看出L29VSIQ快速上升，临近电压崩溃时甚至超过了L20VSIQ，仅次于L21VSIQ。可见节点29对系统无功功率变化十分敏感，需要引起重视。

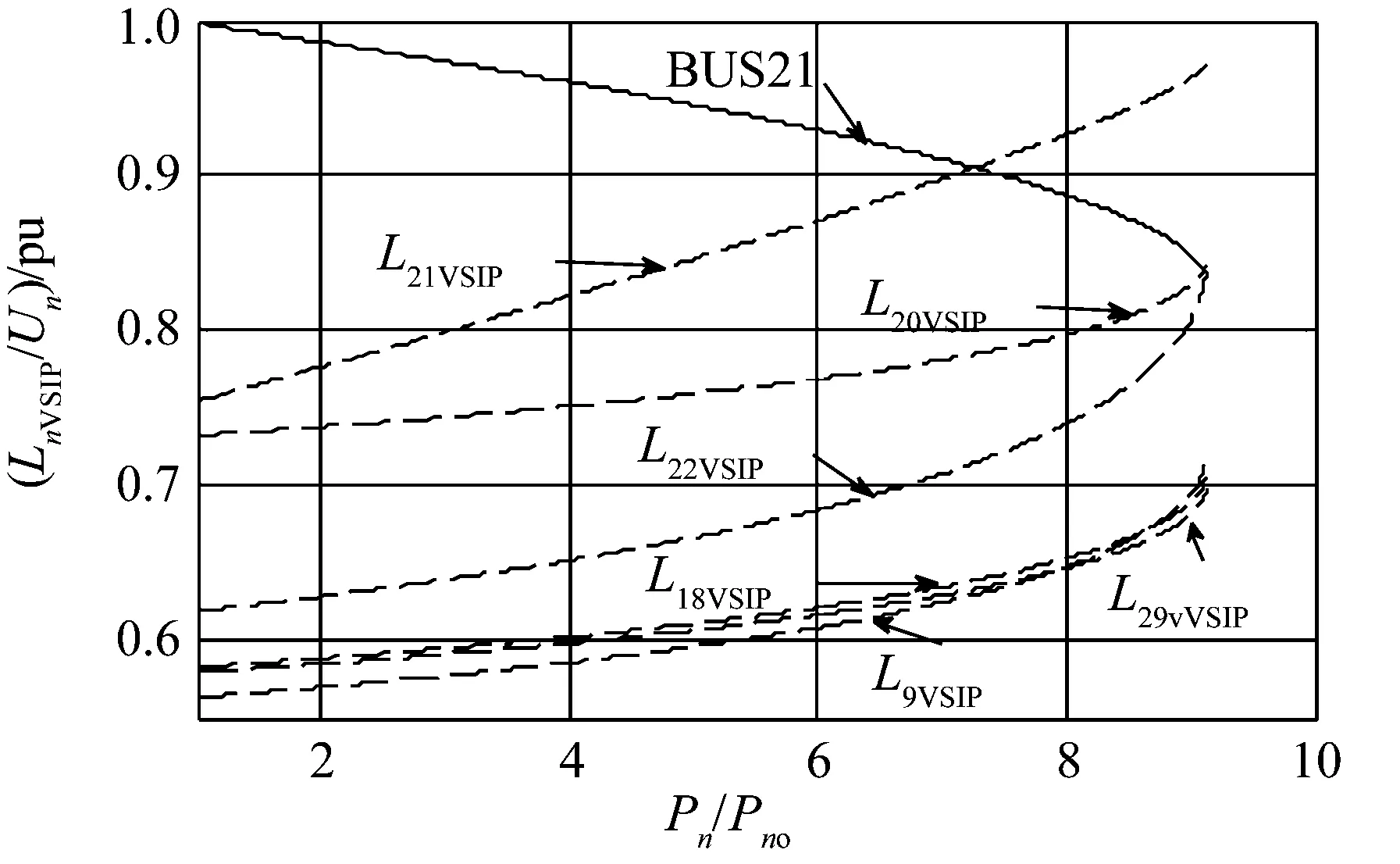
图10 以恒功率因数0.95增加节点 21负荷时的电压稳定有功功率指标Fig.10 Voltage stability index of active power with the 21st bus’s load increasing by the power factor 0.95

(3)综合分析

1)节点18的电压稳定有功功率指标和无功功率

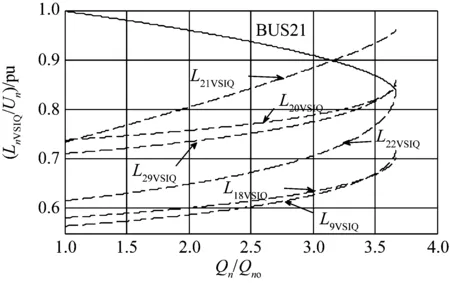
图11 以恒功率因数0.95增加节点 21负荷时的电压稳定无功功率指标Fig.11 Voltage stability index of reactive power with the 21st bus’s load increasing by the power factor 0.95

指标曲线(L18VSIP和L18VSIQ)都较低，甚至其电压稳定指标曲线(L18VSI)表现为系统最低，但是其电压幅值下降值却不是最小的，再次说明不能简单地以负荷节点电压降落大小来判断系统电压稳定水平。

2)图11中，随着无功功率的增加，系统无功功率最弱节点从节点20向节点21转移，较好地反映了系统的无功功率最弱节点变化情况。而在这方面，LnVSI指标是做不到的，因此把节点的LnVSIQ指标(和LnVSIP指标)作为对LnVSI指标的补充是有必要的。

通过对比2个仿真算例还可以发现：节点18在两次仿真中都表现出较高的电压稳定性(L18VSI、L18VSIP和L18VSIQ曲线都较低)，这是因为节点18通过变压器与电源相连(电气距离为j 0.037 5 pu)，还与节点16相连(电气距离为0.003 3 + j 0.033 3 pu)，节点16处安装有无功功率补偿装置，电源和无功功率补偿装置对节点电压具有支撑作用，使得节点18的电压始终保持在较高水平。

系统负荷节点的Un-Pn/Pno曲线和Un-Qn/Qno曲线非常相似，这是因为PSASP采用节点有功功率和无功功率同步增长的方式进行仿真的；而节点的电压稳定有功功率指标曲线和无功功率指标曲线相差较大，这是因为它们由不同的变量因子决定的(具体表达式见式(15)和式(19))。

3.3 与其他指标对比分析

式(20)中的4个电压稳定指标[18,23-25]在电压崩溃点处临界值也为1。

(20)

为使指标之间具有可对比性，上述4个指标也采用本文提供的网络等值模型。在上述2个仿真事例中同时计算5个指标，系统临近电压崩溃点时的计算结果如表1所示。

表1 临近系统崩溃点时的各指标值

Table 1 Each inex on system critical point

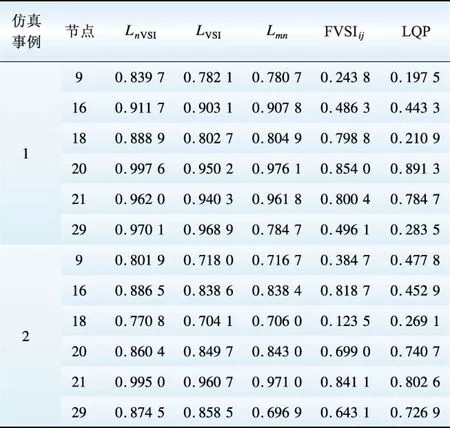
由表1可知，本文研究提出的指标能较好地反映系统临近电压崩溃时的稳定状态，其他指标则相对较差。这是因为这些指标不能综合考虑被测节点的有功功率和无功功率变化，与实际系统存在较大差别。

3.4 实例分析

本小节以山东电网500 kV主网为例(如图12所示)，按照前述2种负荷波动形式对山东省500 kV主网进行计算机仿真，简要说明本文所提指标在实际系统中的适用性。系统临近电压崩溃点时的计算结果如表2所示。表2中，事例1为所有节点负荷以初始功率的10%增加的情况；事例2为单独增加淄博节点负荷(增加量保持恒功率因数)的情况。

从表2中可以看出，当全网节点负荷同步增加时，德州节点率先达到电压不稳定点。同时，潍坊、鲁中节点也具有较小的电压稳定裕度。单独增加淄博节点负荷，使得该节点电压失稳，潍坊节点LnVSI指标受其影响急剧上升，虽未超越淄博节点的LnVSI指标，但从中可见节点电压失稳对其周边节点，尤其是对周边重负荷节点影响甚大(潍坊节点在事例1中就表现出较低的电压稳定裕度)。

在仿真中发现，按山东电网500 kV主网各节点规划负荷进行电压稳定裕度评估，其3项指标均较低，体现出山东500 kV主网具有较高的电压稳定裕度。

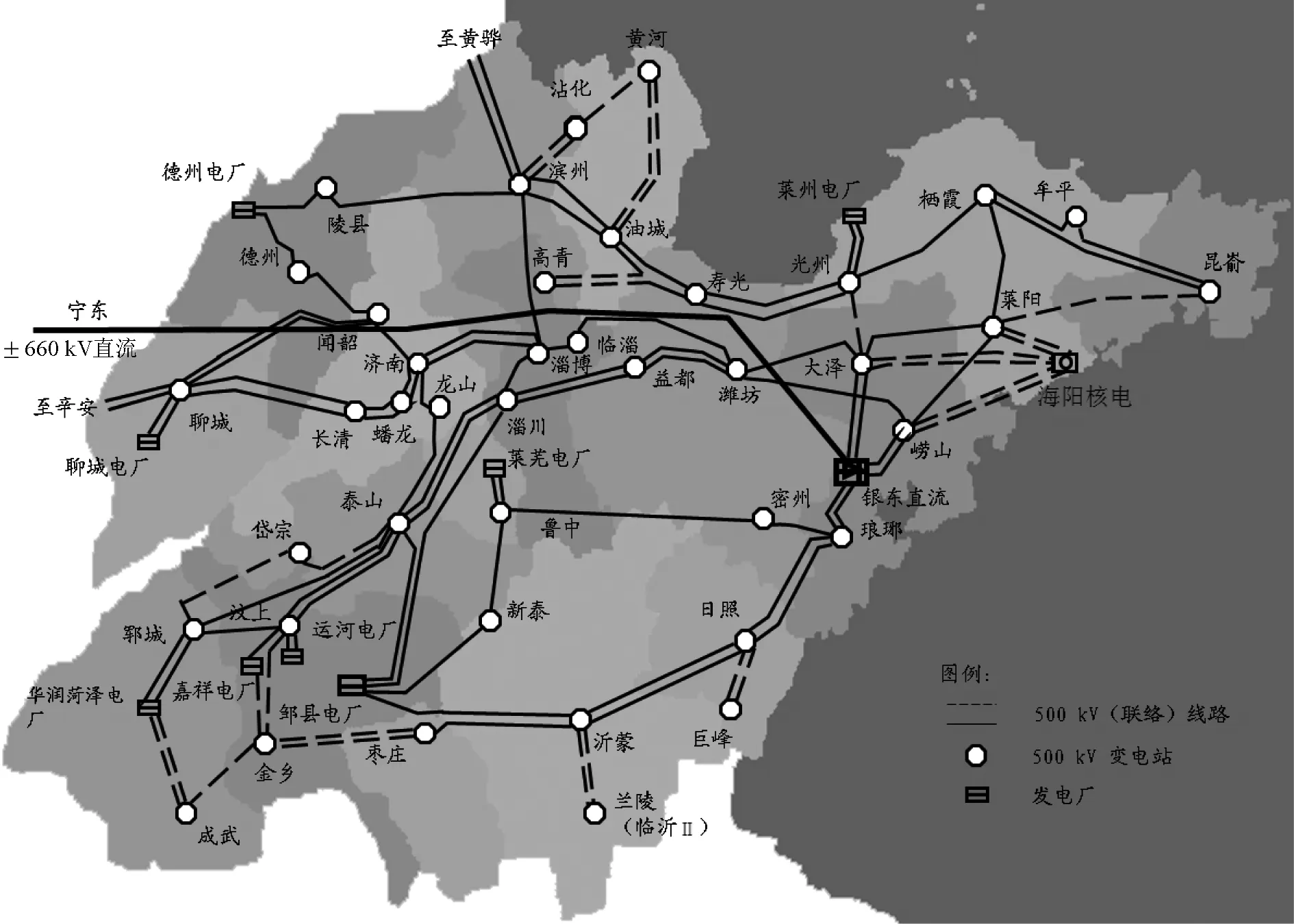
图12 山东电网500 kV主网架接线图(2015年)Fig.12 500 kV main network of Shandong grid (2015)表2 山东电网500 kV主网临近系统崩溃点时各节点指标值Table 2 Nodal indices on system critical point of 500 kV Shandong grid

综上所述，在系统负荷逐渐变化的过程中，指标LnVSI能较好地反映系统静态电压稳定裕度的变化情况。在系统趋于电压崩溃的过程中，总存在LnVSI值最大的负荷节点，其值跟随电压变化并趋近于1。

4 结 论

本文提出的节点电压稳定指标采用了网络等值模型，考虑了被测负荷节点相关支路网络的影响，更接近输电网络的实际情况；指标参数可以由PMU实时测得，可实现在线电压稳定监测和预估。本文提出使用在线电压稳定有功功率指标LnVSIP和在线电压稳定无功功率指标LnVSIQ分别表征节点的有功功率裕度和无功功率裕度，并由综合考虑了有功功率和无功功率的电压稳定指标LnVSI作为负荷节点的在线电压稳定裕度指标，计算简单、快速，具有一定的工程实用价值。

数值仿真分析结果表明：在线电压稳定有功功率指标和在线电压稳定无功功率指标反映了节点电压分别关于其有功功率和无功功率的稳定状况；在线电压稳定指标综合反映了电力系统的电压稳定状况。

[1]薛禹胜.综合防御由偶然故障演化为电力灾难—北美“8.14”大停电的警示[J].电力系统自动化，2003，27(18)：1-5. XUE Yusheng.The way from a simple contingency to system-wide disaster: lessons from the eastern interconnection blackout in 2003[J]. Automation of Electric Power Systems，2003，27(18)：1-5.

[2]唐桃波, 夏云非, 鲁文, 等.美国近年的停电事故及对我国电力系统安全稳定运行的启示[J].电力建设，2003，24(11)：2-4. TANG Taobo, XIA Yunfei, LU Wen, et al. Power failure of this year in USA and its inspiration to safe stable operation of power system in China[J]. Electric Power Construction, 2003, 24(11): 2-4.

[3]阮前途，马若新，肖飞，等. 菲律宾吕宋电网系统崩溃及黑启动措施分析[J]. 电力系统自动化，2011, 35(4): 82-91. RUAN Qiantu, MA Ruoxin, XIAO Fei, et al.Blackout and restoration experience in Luzon Grid[J]. Automation of Electric Power Systems，2011，35(4)：82-91.

[4]汤涌，卜广全，易俊.印度“7.30”、“7.31”大停电事故分析及启示[J] .中国电机工程学报，2012，32(25)：167-174. TANG Yong，BU Guangquan，YI Jun.Analysis and lessons of the blackout in Indian power grid on July 30 and 31, 2012[J].Proceedings of the CSEE，2012，32(25)：167-174.

[5]李佳，刘天琪，陈亮，等.基于理想点法的多准则综合灵敏度电压稳定评估指标[J].电力自动化设备，2014，34(3)：108-112. LI Jia，LIU Tianqi，CHEN Liang，et al.Multi-criterion integrated-sensitivity voltage stability evaluation index based on ideal point method[J]. Electric Power Automation Equipment，2014，34(3)：108-112.

[6]李帅虎，曹一家，刘光晔，等.基于电压稳定在线监测指标的预防控制方法[J].中国电机工程学报, 2015, 35(18): 4598-4606. LI Shuaihu, CAO Yijia, LIU Guangye, et al.Preventive control method of electric power system based on on-line voltage stability monitoring index[J]. Proceedings of the CSEE, 2015, 35(18): 4598-4606.

[7]SMON I, PANTOS M, GUBINA F. An improved voltage-collapse protection algorithm based on local phasors[J].Electric Power Systems Research，2008，78(3): 434-440.

[8]王庆红，CHEN K. 基于试验函数的霍普夫分岔搜索新算法与电压稳定指标分析[J].电工技术学报，2008，23(1)：120-128. WANG Qinghong，CHEN K. Novel algorithms based on test function for tracing hopf bifurcation and analysis of power system voltage stability index[J].Transactions of China Electrotechnical Society，2008，23(1)：120-128.

[9]周任军，吴潘，童小娇.极限诱导分岔最小负荷裕度计算方法[J].电力自动化设备，2010，30(7)：19-23. ZHOU Renjun，WU Pan，TONG Xiaojiao.Calculation of minimum load power margin for limit induced bifurcation [J]. Electric Power Automation Equipment，2010，30(7)：19-23.

[10]张晓英, 蒋拯, 丁宁, 等. 负荷裕度及其与典型参数的灵敏度计算[J].电机与控制学报, 2015, 19(8): 28-35. ZHANG Xiaoying, JIANG Zheng, DING Ning, et al. Load margin and its sensitivity calculation with typical parameters[J]. Electric Machines and Control, 2015, 19(8): 28-35.

[11]姜涛，李国庆，贾宏杰，等.电压稳定在线监控的简化L指标及其灵敏度分析方法[J].电力系统自动化，2012，36(21)：13-18. JIANG Tao，LI Guoqiang，JIA Hongjie，et al.Simplified L-index and its sensitivity analysis method for on-line monitoring of voltage stability control[J].Automation of Electric Power Systems，2012，36(21)：13-18.

[12]苏永春，程时杰，文劲宇，等. 电力系统电压稳定性及其研究现状(一)[J].电力自动化设备，2006，26(6)：97 - 101. SU Yongchun，CHENG Shijie，WEN Jinyu，et al. Power system voltage stability and its present investigation (I)[J]. Electric Power Automation Equipment，2006，26(6)：97-101.

[13]吴政球, 李日波, 钟浩, 等. 电力系统静态电压稳定极限及裕度计算综述[J]. 电力系统及其自动化学报, 2010, 22(1): 126-132. WU Zhengqiu, LI Ribo, ZHONG Hao, et al. Summary of power system’s static voltage stability limitation and load margin calculation[J]. Proceedings of the CSU-EPSA, 2010, 22(1): 126-132.

[14]LIU J H, CHU C C. Wide-area measurement-based voltage stability indicators by modified coupled single-port models[J]. IEEE Transactions on Power Systems, 2014, 29(2): 756-764.

[15]GHIOCEL S G, CHOW J H. A power flow method using a new bus type for computing steady-state voltage stability margins[J].IEEE Transactions on Power Systems, 2014, 29(2): 958-965.

[16]HAZARIKA D. New method for monitoring voltage stability condition of a bus of an interconnected power system using measurements of the bus variables[J]. IET Generation, Transmission & Distribution, 2012, 6(10): 977-985.

[17]ALTHOWIBI F A, MUSTAFA M W. Voltage stability calculations in power transmission lines：Indications and allocations[C]// 2010 IEEE International Conference on Power and Energy (PECon). Kuala Lumpur: IEEE, 2010: 390-395.

[18]刘道伟, 谢小荣, 穆钢, 等. 基于同步相量测量的电力系统在线电压稳定指标[J]. 中国电机工程学报, 2005, 25(1): 13-17. LIU Daowei, XIE Xiaorong, MU Gang, et al. An on-line voltage stability index of power system based on synchronized phasor measurement [J]. Proceedings of the CSEE, 2005, 25(1): 13-17.

[19]汪洋，卢继平，李文沅，等.基于局部网络电压相量的等值模型及其电压稳定性指标[J].中国电机工程学报，2008，28(34)：52-58. WANG Yang, LU Jiping, LI Wenyuan, et al. An equivalent model and voltage stability index based on local network voltage phasors [J].Proceedings of the CSEE，2008，28(34)：52-58.

[20]汤涌.电力系统电压稳定性分析[M].北京：科学出版社，2011：107-110.

[21]周双喜，朱凌志，郭锡玖，等.电力系统电压稳定性及其控制[M].北京：中国电力出版社，2003：162-168.

[22]JOHNSON M, VAZIRI M, VADHVA S. Understanding slow voltage instability [C]//2012 IEEE 13th International Conference on Information Reuse and Integration (IRI). Las Vegas, NV: IEEE, 2012: 502-508.

[23]MOGHAVEMMI M, OMAR F M. Technique for contingency monitoring and voltage collapse prediction [J]. IEE Proceedings-Generation, Transmission and Distribution. 1998, 145(6): 634-640.

[24]MUSIRIN I， RAHMAN T K A.Novel fast voltage stability index (FVSI) for voltage stability analysis in power transmission system[C]// Research and Development, 2002. SCOReD2002. Student Conference on. Shah Alam，Malaysia: IEEE, 2002: 265-268.

[25]MUSIRIN I, RAHMAN T K A.Estimating maximum load ability for weak bus identification using FVSI [J].IEEE Power Engineering Review, 2002, 22(11): 50-52.

(实习编辑 景贺峰)

Load-Nodal On-Line Voltage Stability Index for Power System

GAO Feng1, WANG Yanwen1, GUO Lin1, XU Rui2

(1. China University of Mining & Technology (Beijing), Beijing 100083, China;2. Dezhou Power Supply Company,State Grid Shandong Electric Power Company, Dezhou 253000, Shandong Province, China)

This paper applies phasor measurement unit (PMU) to measure the real-time data including the voltage and power flow of any (non PV) node and adjacent busbar, and constructs a network equivalent model. Meanwhile, we present the on-line voltage stability index with comprehensive consideration of the active power and reactive power of load node based on this model. And we suggest that the on-line voltage stability indexes of active power and reactive power can be used as active power or reactive power margin for the characterization of load node respectively, which can be the supplement to the on-line voltage stability index of node (system). If the on-line voltage stability index of load note approaches to 1, it shows that the power system draws near voltage collapse. Simulation results of EPRI-36 bus system show that the proposed method can effectively judge the system voltage stability, and is suitable for the monitoring and prediction of on-line voltage stability. Compared with other indexes, the rationality and superiority of the proposed model and index are reflected. Finally, we briefly explain the feasibility of the proposed method through the voltage stability margin evaluation of load node in Shandong 500 kV main network.

voltage stability; on-line voltage stability index; phasor measurement unit(PMU); network equivalent model

“十二五”国家科技支撑计划重大项目(2012BAK04B00)

TM 712

A

1000-7229(2016)02-0069-09

10.3969/j.issn.1000-7229.2016.02.010

2015-10-27

高峰(1988)，男，博士研究生，主要研究方向为广域同步测量技术和电力系统分析；

王彦文(1962)，男，博士，教授，主要研究方向为广域同步测量系统、网络型继电保护技术等；

郭林(1986)，男，博士研究生，主要研究方向为网络型继电保护技术；

徐睿(1989)，男，硕士，工程师，主要研究方向为电网安全运行及电网调度控制。

Project supported by key Project of the National Twelfth-Five Year Research Program of China((2012BAK04B00))