超声速降落伞系统的气动干扰数值模拟研究

薛晓鹏温志湧



超声速降落伞系统的气动干扰数值模拟研究

薛晓鹏1温志湧2

（1 中南大学航空航天学院，长沙410083）（2 香港理工大学深圳研究院，深圳 518057）

文章基于一种简易“浸入边界技术”与流固耦合方法对超声速来流条件下的三维降落伞系统进行了数值模拟。文章分析了降落伞系统（太空舱和降落伞衣）流场产生的气动干扰对伞衣外形变形动力学的影响以及降落伞设计参数（如拖拽距离参数）对降落伞性能表现的影响，同时检验了分离涡模拟方法在三维超声速降落伞数值模拟中的适用性。结果表明，当拖拽距离参数很小时，伞衣出现了严重的收缩现象；当距离增大时，观测到了伞开口的“呼吸现象”，阻力系数获得了较大改善。另外，在拖拽距离参数较大的情况下，由于湍流尾流与伞前激波的气动干扰影响明显，采用分离涡模拟方法，可以获得较层流尾流条件下更大的阻力系数。

气动干扰分离 涡模拟 流固耦合 超声速降落伞

0 引言

在NASA的“火星科学实验室”（MSL）任务中，“好奇号”探测器已经成功地着陆在火星表面。“好奇号”在进入火星大气层以后的从超声速到亚声速的减速过程是由一个超声速降落伞系统所完成的[1]。

从20世纪60年代末开始，超声速降落伞的研究工作吸引了全世界的研究学者。文献[2]用风洞试验方法检验了前置体尾流影响下的多种类型的超声速盘缝带伞系统的气动特性。文献[3-4]利用计算流体力学方法和流固耦合方法（Fluid Structure Interaction，FSI）首次对柔性超声速降落伞进行了数值模拟，并观测到了其周围以尾流—激波相互作用为主要特征的复杂流场结构，同时分析了马赫数和拖拽距离参数对伞衣阻力系数的影响。近年来，美国NASA及其合作小组对MSL降落伞模型进行了超声速条件下试验和数值的充分调查[5-7]，发现降落伞不稳定主要来自于降落伞前激波与太空舱尾流的气动干扰，其将导致伞前激波形状的变化，进而减少质量流流进伞内部，并且该非定常气动干扰受马赫数、雷诺数、太空舱形状以及舱与伞的距离等因素的影响。文献[8]使用大涡模拟方法和基于有限元模型的结构膜对大尺度超声速盘缝带伞进行了数值模拟，并成功观测到了降落伞体的“呼吸现象”（开口面积出现在一定范围内波动）。文献[9]使用浸入边界技术以及流固耦合方法对三维超声速降落伞进行数值模拟，进一步分析了拖拽距离参数、太空舱以及伞体形状、马赫数对降落伞性能的影响。近年来，我国有关超声速降落伞及火星环境下的减速着陆研究也开始启动：文献[10]利用径向—轴向动量守恒充气模型研究大气密度对降落伞的开伞过程的影响，结果表明降落伞的充气时间和充气距离随大气密度的减小而增大；文献[11]进一步计算了低密度大气中盘缝带降落伞的开伞动载；文献[12]进一步简化了降落伞的轴向—径向动量方程，分析了不同大气密度、初始开伞速度下的充气环境对降落伞开伞过程的影响；文献[13]探讨了结构参数对火星用伞开伞性能的影响，发现当盘缝带伞的带宽和缝宽增加，该伞的阻力系数随之减少；文献[14]通过高速风洞试验以及高速飞行投放试验对超声速半流伞进行了结构设计和气动特性分析，得到了半流伞的摆角参数和阻力系数变化规律。

随着计算机技术的发展，降落伞问题的数值模拟已经取得了显著的进步。一些成功的方法，比如变空间域/稳定时间—空间（Deforming-spatial-domain/stabilized Space-time，DSD/SST）方法[15]、任意拉格朗日—欧拉法（Arbitrary Langrangian Eulerian，ALE）[16-17]、浸入边界法（Immersed Boundary Method，IBM）[18]等，已经成功应用到亚声速降落伞数值模拟中。但是，至今还没有合适的数值方法求解超声速降落伞问题。Lingard在超声速降落伞的数值模拟中采用了ALE方法，然而未能展示复杂流动现象影响下伞衣的外形变化[3-4]。本研究中我们提出了一种简易浸入边界技术（Immersed Boundary Technique，IBT）应用到涉及超声速降落伞模型的流固耦合问题中。该方法已经被成功应用到亚声速超声速降落伞系统的二维和三维的数值模拟[19]中，模拟所得的开伞过程与试验结果非常吻合。该方法也被应用到了超声速降落伞的数值模拟[9]，并得到了与美国NASA的喷气推进实验室的超声速降落伞试验一致的结果。另外，该技术也被应用在降落伞伞绳在超声速流场中的影响的数值模拟中，并观测到了伞绳激波，其与美国NASA喷气推进实验室对该研究的试验结果保持一致[20]。

在高马赫数、高雷诺数情况下，太空舱尾流将是复杂的湍流流动，降落伞周围流场将出现强烈的太空舱湍流尾流与伞前激波的气动干扰并伴有复杂的流场结构。本研究将对三维超声速降落伞进行数值模拟，分析气动干扰对降落伞伞衣变形动力学的影响，以及降落伞设计参数如拖拽距离参数对降落伞性能表现的影响，同时检验分离涡模拟（Detached Eddy Simulation，DES）方法在三维超声速降落伞数值模拟中的适用性。

1 三维降落伞模型

本研究中的三维降落伞系统包括太空舱和降落伞伞衣，如图1所示。伞衣和太空舱之间用伞绳连接，这里伞绳的作用仅是维持伞体和太空舱之间的受力平衡。伞绳以及透气量对流场的影响暂且不考虑。

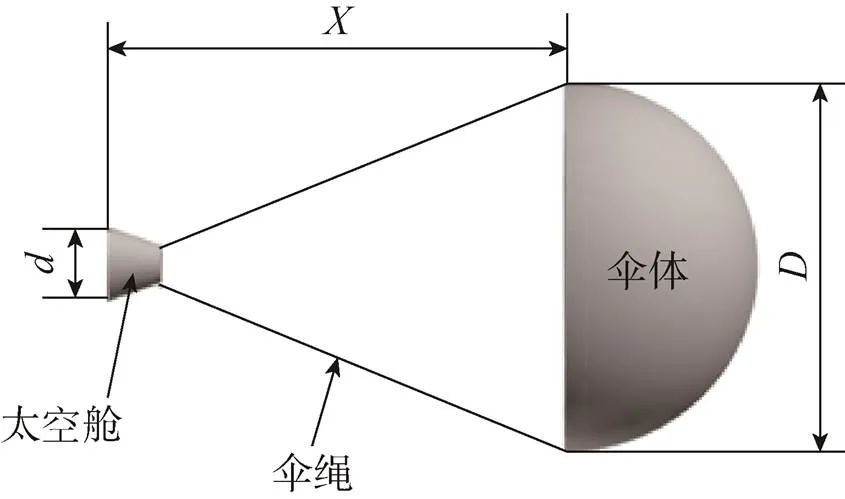
图1 三维降落伞模型

伞体是一个直径为的半球简化模型，太空舱是一个呈锥形的简化模型，半锥角为20°，前表面的直径是=24mm。是从太空舱前表面到伞体入口的直线距离。是降落伞的关键设计参数，即拖拽距离参数。本研究中模型A和B的拖拽距离参数如表1所示，其数值小于NASA的MSL降落伞模型试验中的名义值（大约为10），这是因为在小于10的情况下，更加复杂的气动干扰在以前刚性处理的降落伞模型研究中被观测到[21]，因此发生在更复杂情况下的柔性降落伞的性能表现是值得研究的。

表1 降落伞系统外形参数

Tab.1 Specifications for the different parachute systems

2 数值方法

2.1 计算条件和计算网格

本研究计算中来流条件如表2所示，来自于文献[22]中的试验条件。由于降落伞系统的轴对称特性，计算网格由子午线断面旋转而成，如图2所示，图中红色部分是伞体，蓝色部分是太空舱。网格单元数约1×106个。降落伞伞体的控制点数目为902×441，其在伞体区域被搜索定义，网格依赖性检验参考文献[9]。

表2 本研究计算所用的来流条件

Tab.2 Free stream conditions employed in this study

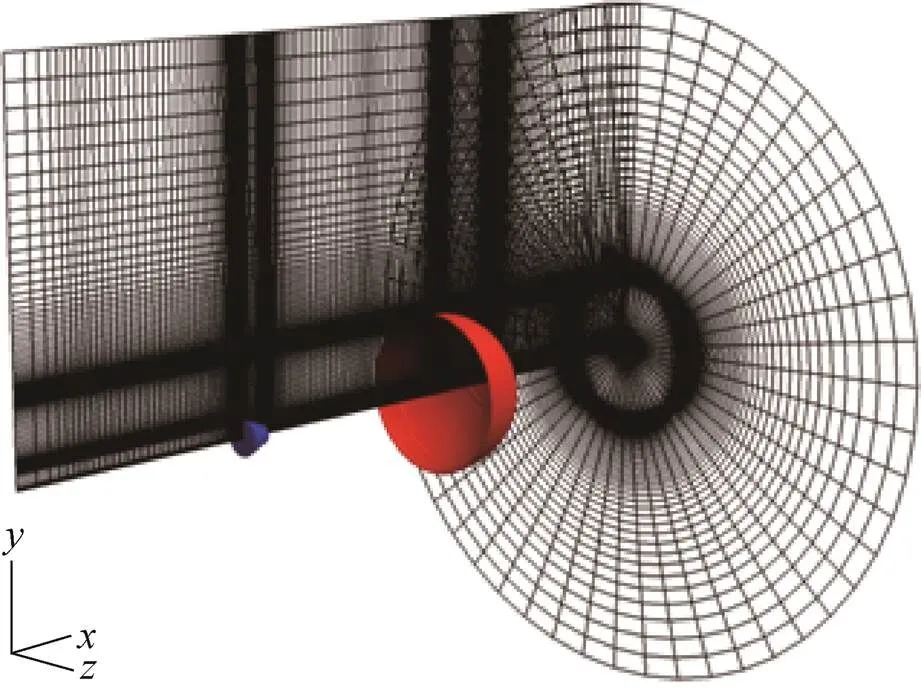
图2 降落伞的计算网格

2.2 数值方法

（1）流场计算

本研究采用三维可压缩Navier-Stokes方程数值求解三维降落伞系统周围的超声速流场，控制方程采用有限体积法进行离散。无粘通量选择SHUS（Simple High-resolution Upwind Scheme）[23]格式，并采用Van Albada限制器通过3阶MUSCL（Monotone Upstream-centered Schemes for Conservation Law）方法进行差值提高精度。粘性通量采用2阶中心格式离散，时间推进则采用LU-SGS（Lower-upper Symmetric Gauss-seidel Method）格式进行。边界条件的处理上，太空舱面采用无滑移、等壁温。入口边界赋来流参数，出口边界采用外插处理。

本研究采用了“浸入边界技术”来处理三维降落伞的柔性伞体部分。该技术是由Ochi[24]等人提出，由Miyoshi、Xue等人发展而成适用于低速、高速流场中降落伞的流固耦合研究中的一种简易技术[9,19]。该浸入边界技术有别于传统的“浸入边界法”[25]。因为传统的浸入边界法受限于低雷诺数和不可压流，且在流场控制方程中增加了力源项，该力源项在严格限制中常常表现不佳。而本浸入边界技术未在控制方程中引入一个力源项，而是通过流体网格和虚拟网格的关系来求得虚拟网格的速度向量，如图3所示，其求解方程[9,19]为：

V=V-2(V·n)n+V（1）

式中V,V, V分别代表流体网格、虚拟网格和伞控制点的速度；V在壁面上可以分解为垂直方向和平行方向分量V和V；n代表伞表面的单位法向量；下标和分别表示流体网格和虚拟网格的变量。式（1）展开以后正如图3中右图所示的关系[9,19]。方程的详细推导过程参考文献[24]。

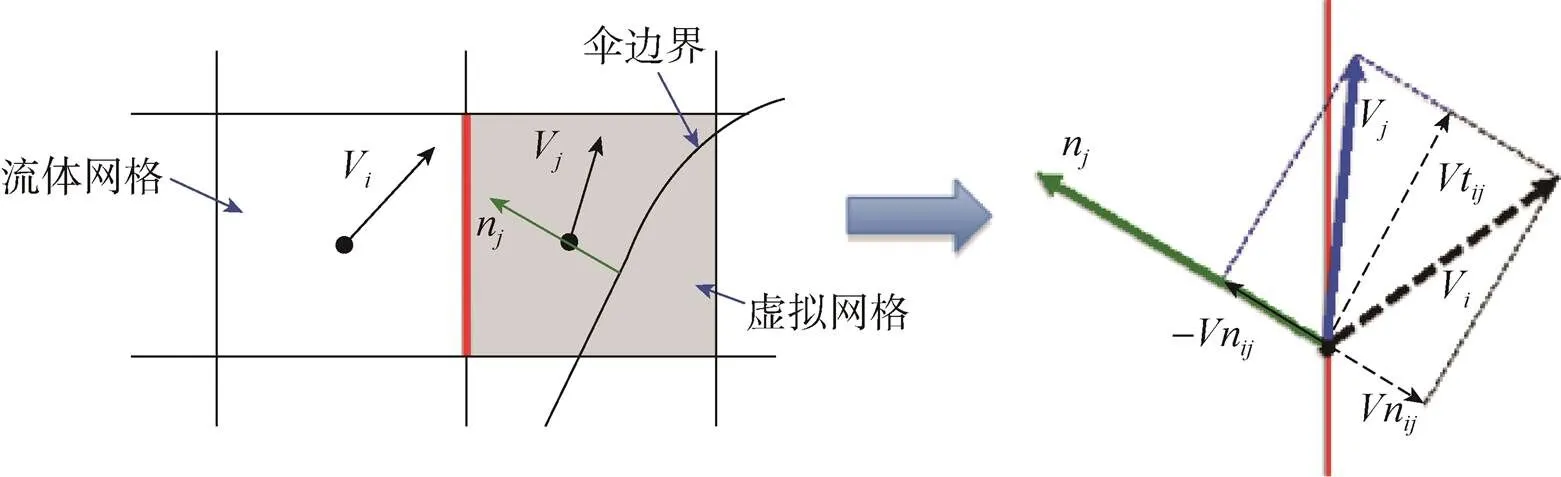
图3 虚拟网格和流体网格的速度之间的关系[9,19]

太空舱的尾流将呈以大尺度涡为特征的高度湍流状态，并与来自伞体的激波发生激烈气动干扰[5]。本文采用DES方法[26-27]对其进行湍流模拟。DES是一种混合模型，其在计算时，近壁面湍流结构的计算求解雷诺平均N-S方程（Reynolds Averaged Navier-stokes Equation，RANS）得到耗散能量的小涡，同时远离壁面的分离涡明显的区域则采用大涡模拟方法（Large Eddy Simulation, LES）求解。本研究中的RANS模型采用的是方程Spalart-Allmaras（S-A）模型。DES处理RANS和LES过渡区域的方法是借用S-A模型控制方程中的参数，这一参数表示了网格节点与最近壁面的距离。因为需要根据不同距壁面距离来确定相应的求解方法，DES方法对参数进行了修正，定义了新的长度尺度,其由壁面距离和当地网格尺度共同确定：

（2）结构计算

在本研究中，降落伞模型的结构计算采用了质量−弹簧−阻尼模型[9,19,28]来模拟伞体的结构动力学，如图4所示。在该模型中，伞结构被处理为质点与弹簧和阻尼的联合体，特别在伞的边缘，需要考虑来自伞绳的拉力。其控制方程是基于作用在伞的每个控制点的牛顿第二定律。伞体结构计算的时间推进算法采用显性2阶Runge-Kutta 格式。

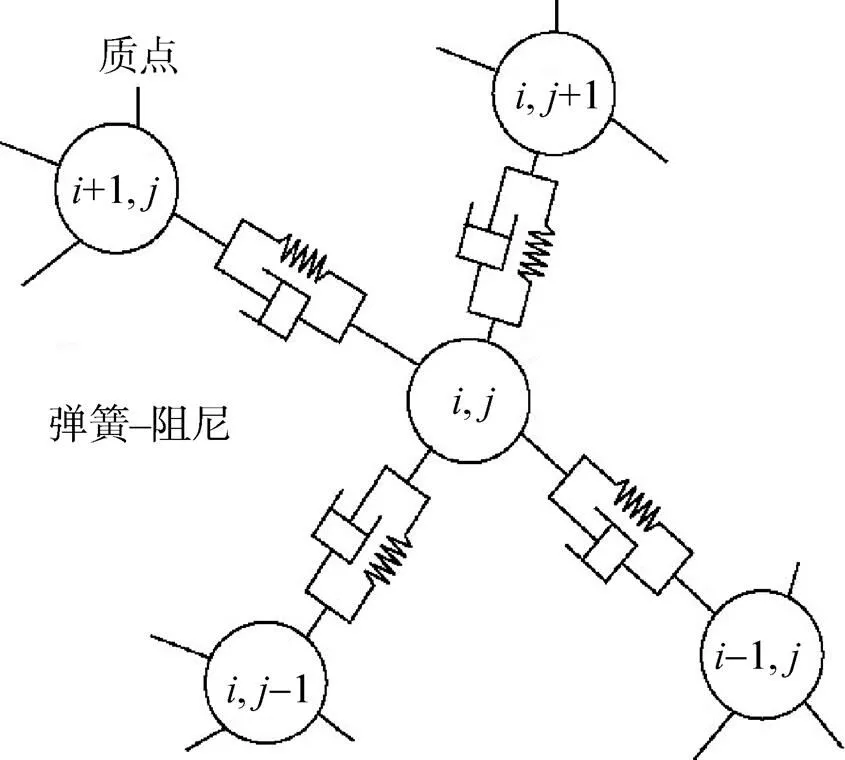
（a）伞内部的MSD模型 （b）伞边缘的MSD模型

（a）General MSD model （b）Special MSD model on the edge of canopy

图4 伞的质量−弹簧−阻尼结构模型[9,19]

Fig.4 The MSD model

（3）流固耦合格式

流固耦合方法如图5所示，伞体表面上的压力分布做为流体力，被应用到每一个伞体控制点的位移和速度计算中[9,19]，然后这些计算结果作为边界条件再通过耦合方法“浸入边界技术（IBT）”[9,19]被传送到流场计算中。

为了同时计算流体和结构，弱耦合方法（如图6所示，图中为时间步长）被应用到该计算中，因为伞体变形和非定常流场的相互影响非常敏感[9]。

图5 流固耦合方法[9]

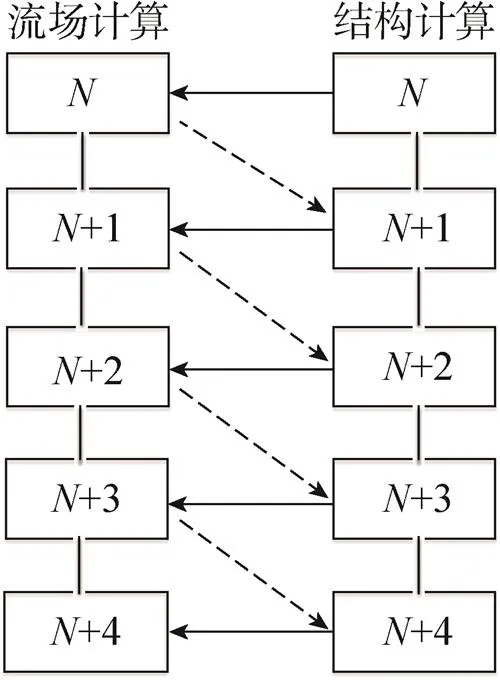
图6 弱耦合格式[9]

3 计算结果与分析

3.1 模型A：=57mm，=2.375

图7 模型A伞衣的外形变化

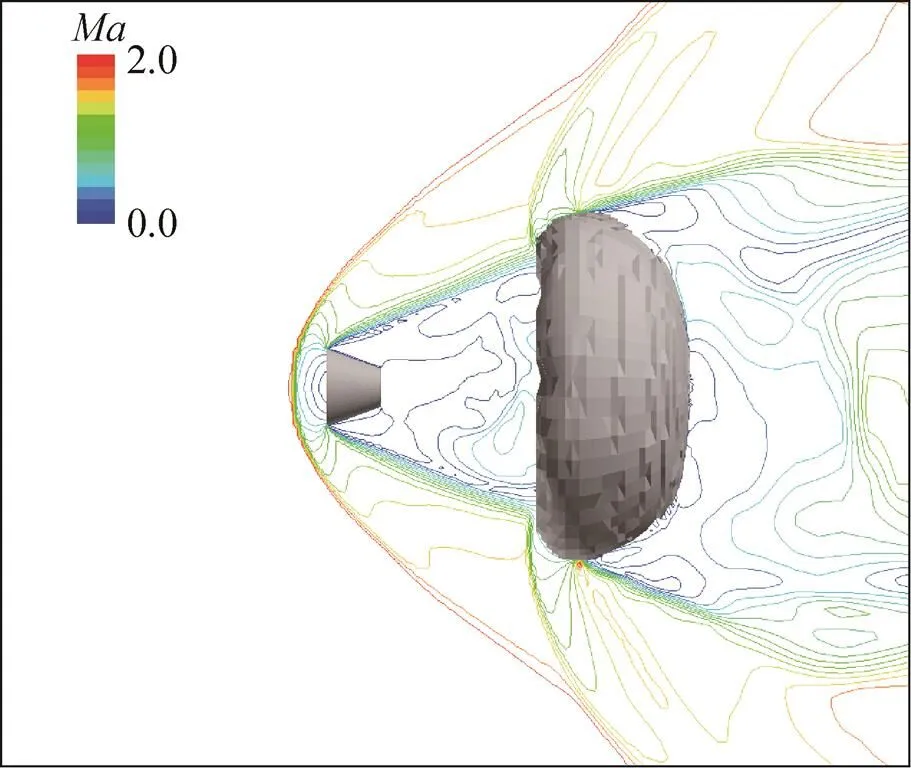
图8 模型A降落伞系统的瞬时马赫数等值线

强烈的流场不稳定会导致伞衣的阻力d出现很大的不稳定状态，该阻力作用在来流方向，可由伞衣表面的内外压力差计算。然而，为了更精确的定义和比较，阻力系数被用来表征降落伞系统的性能。阻力系数d[7]定义如下：

图9比较了模型A的湍流模型（DES）和层流模型（Laminar）的阻力系数曲线，图中层流结果（Laminar）来自文献[9]。从图中可以发现，大约0.003~0.004s开始，其阻力系数已经基本上减小至零，这是因为该模型伞衣在持续地收缩，使得内外压差持续减小至零。在0.003s之前，由于0s时候的伞衣处于半球形状，伞前激波与太空舱尾流发生激烈气动干扰，导致伞内压力急剧上升，并得到极大的阻力系数。当伞内压力达到波谷的时候，伞的阻力变得很小，严重的伞衣收缩使得阻力系数逐渐减小至零。

图9 模型A（X=57mm）降落伞系统的阻力系数

另外值得注意的是，与文献[9]中层流计算结果相比较，伞衣外形变化、降落伞周围流场结构与气动干扰位置和阻力系数变化受湍流计算影响较小。所以，拖拽系数较小时，太空舱尾流与伞前激波始终在伞端部发生气动干扰，导致伞衣严重收缩，进而使其阻力系数急剧减小，降落伞性能失效。

3.2 模型B：=171mm，=7.125

图10为模型B的伞衣外形变化，与模型A相比，可以观察到伞衣开口呈现出“呼吸现象”。图11为模型B周围的流场分布，伞前激波在伞开口的逆流方向与来自太空舱的湍流尾流发生剧烈气动干扰，这是降落伞周围流场不稳定的主要来源[7-8]。因为拖拽距离参数增大，所以太空舱前激波呈现稳定状态，未与伞前激波发生干扰。图12为该模型的阻力系数曲线（图中层流结果（Laminar）来自文献[9]），与图9模型A相比，可以发现模型B产生了较高的阻力系数，并出现周期变化。所以，适当增加拖拽距离系数，降落伞系统可以得到较高的阻力系数，这与Reichenau[2]的实验发现是吻合的，与文献[9]中层流情况下的计算结果也是保持一致的。

另外，与文献[9]层流结果相比，伞衣外形变化与流场结构特征保持一致，从图12中层流（Laminar）与湍流（DES）模型结果相比较，可以发现稳定阶段（0.003s以后）湍流计算所得阻力系数与层流结果变化趋势基本保持一致，但是幅值要较层流大。这说明太空舱后的湍流尾流与激波气动干扰较层流尾流情况下增强，阻力系数显著增大。

图10 模型B伞衣的外形变化

图11 模型B降落伞系统的瞬时马赫数等值线

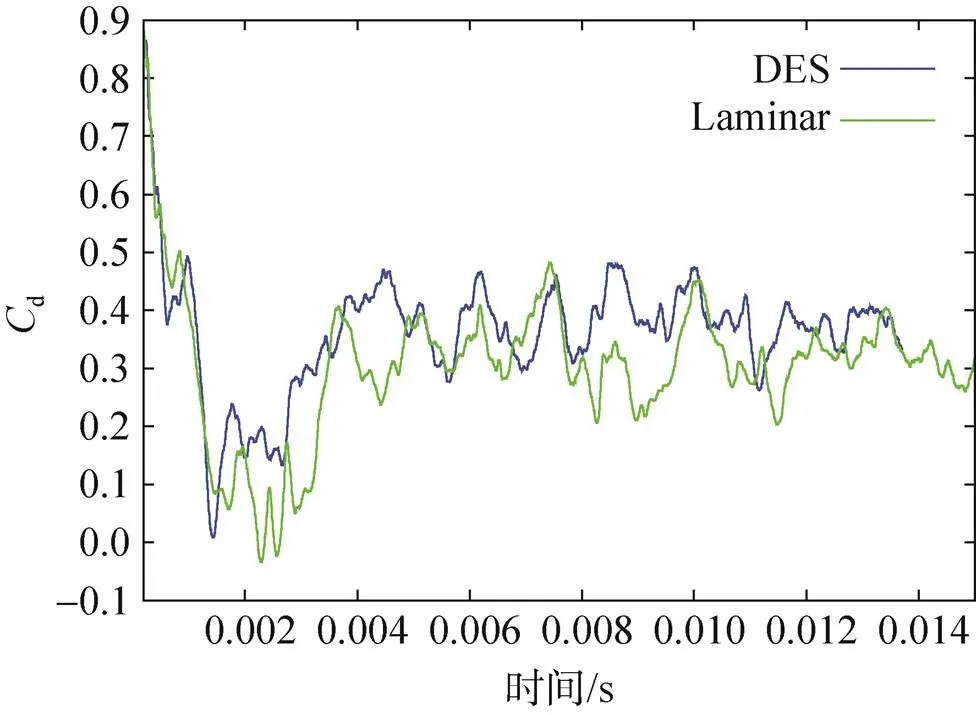
图12 模型B（X=171mm）降落伞系统的阻力系数

4 结束语

本文主要分析了降落伞系统周围复杂的气动干扰对降落伞伞体变形动力学的影响，以及降落伞设计参数，如拖拽距离参数对降落伞性能表现的影响。在高马赫数、高雷诺数的条件下，检验了分离涡模拟方法在三维超声速降落伞数值模拟中的必要性与适用性。结果表明，影响降落伞性能表现的两大关键因素是降落伞的非定常变形和太空舱尾流与伞前激波的气动干扰。当拖拽距离参数很小时，伞出现了严重的收缩现象；当该距离增大时，观测到了伞开口的“呼吸现象”，并且阻力系数获得了较大改善。分离涡模拟方法对大拖拽距离系数的降落伞系统周围流场复杂气动干扰更敏感，进而影响实际阻力系数的精确度。

保护区，指对水资源保护、自然生态系统及珍稀濒危物种的保护有重要意义，需划定进行保护的水域。禁止在饮用水水源一级保护区、自然保护区核心区等范围内新建、改建、扩建与保护无关的建设项目和从事与保护无关的涉水活动。

[1] SENGUPTA A, STELTZNER A. Results from the Mars Science Laboratory Parachute Decelerator System Supersonic Qualification Program[C]//Aerospace Conference, Big Sky, MT: IEEE, 2008. DOI: 10.1109/AERO.2008.452684.

[2] REICHENAU D E. Aerodynamic Characteristics of Disk-gap-band Parachutes in the Wake of Viking Entry Forebodies at Mach Numbers from 0.2 to 2.6[R]. AEDC-TR-72-78, Tennessee: Arnold AFB, 1972.

[3] LINGARD J, DARLEY M. Simulation of Parachute Fluid Structure Interaction in Supersonic Flow[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA Paper 2005-1607, Munich, Germany, 2005.

[4] LINGARD J, DARLEY M, UNDERWOOD J C. Simulation of Mars Supersonic Parachute Performance and Dynamics[C]// 19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA Paper 2007-2507, Williamsburg, VA, 2007.

[5] SENGUPTA A. Fluid Structure Interaction of Parachutes in Supersonic Planetary Entry[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA Paper 2011-2541, Dublin, Ireland, 2011.

[6] SENGUPTA A, KELSCH R. Supersonic Performance of Disk-gap-band Parachutes Constrained to a 0-Degree Trim Angle[J]. Journal of Spacecraft and Rockets, 2009, 46(6): 1155-1163.

[7] SENGUPTA A, STELZNER A. Findings from the Supersonic Qualification Program of the Mars Science Laboratory Parachute System[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA Paper 2009-2900, Seattle, Washington, 2009.

[8] KARAGIOZIS K, KAMAKOTI R, CIRAK F, et al. A Computational Study of Supersonic Disk-gap-band Parachutes Using Large-eddy Simulation Coupled to a Structural Membrane[J]. Journal of Fluids and Structures, 2011, 27(2): 175-192.

[9] XUE X, NAKAMURA Y. Numerical Simulation of a Three-dimensional Flexible Parachute System under Supersonic Conditions[J]. Trans. JSASS Aerospace Tech. Japan, 2013, 11: 99-108.

[10] 荣伟, 陈旭, 陈国良. 大气密度对降落伞充气性能的影响[J]. 航天返回与遥感, 2006, 27(3): 11-16. RONG Wei, CHEN Xu, CHEN Guoliang. The Effect of Atmospheric Density on Parachute Inflation Performances[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(3): 11-16. (in Chinese)

[11] 荣伟, 陈旭, 陈国良. 低密度大气中降落伞开伞动载的研究[J]. 航天返回与遥感, 2006, 27(4): 7-11. RONG Wei, CHEN Xu, CHEN Guoliang. The Study of the Parachute Opening Load in Low Atmospheric Density[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(4): 7-11. (in Chinese)

[12] 郭树伟, 董杨彪, 王海涛, 等. 降落伞充气环境对充气性能的影响[J]. 中国空间科学技术, 2008, 28(6): 45-51. GUO Shuwei, DONG Yangbiao, WANG Haitao, et al. Influence of Inflation Conditions on Parachute Inflation[J]. Chinese Space Science and Technology, 2008, 28(6): 45-51. (in Chinese)

[13] 连亮, 张红英, 李方. 结构参数对火星探测用伞开伞性能的影响[J]. 航天返回与遥感, 2012, 33(6): 24-29. LIAN Liang, ZHANG Hongying, LI Fang. Influence of Structure Parameters on Inflation Performance of Parachute Used for Mars Exploration[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(6): 24-29. (in Chinese)

[14] 韩晋阳, 徐宏, 高峰. 超声速半流伞设计与分析[J]. 航天返回与遥感, 2013, 34(5): 20-28. HAN Jinyang, XU Hong, GAO Feng. Design and Analysis of Supersonic Half-flow Parachute[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(5): 20-28. (in Chinese)

[15] TEZDUYAR T E, BEHR M, LIOU J. A New Strategy for Finite Element Computations Involving Moving Boundaries and Interfacesthe Deforming-spatial-domain/space-time Procedure: I. the Concept and the Preliminary Numerical Tests[J]. Computer Methodsin Applied Mechanics and Engineering, 1992, 94(3): 339-351.

[16] 陈涵, 余莉, 李少腾, 等. 折叠降落伞展开过程研究[J]. 航天返回与遥感, 2012, 33(2): 1-6. CHEN Han, YU Li, LI Shaoteng, et al. A Study on the Opening Processs of Folded Parachute[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(2): 1-6.(in Chinese)

[17] 陈猛, 王璐, 陈涵, 等. 降落伞充气过程流固耦合方法的数值预测分析[J]. 南京航空航天大学学报, 2013, 45(4): 515-520. CHEN Meng, WANG Lu, CHENG Han, et al. Numerical Prediction Analysis of Parachute Inflation Process Using Fluid-structure Interaction Method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(4): 515-520. (in Chinese)

[18] KIM Y, PESKIN C S. 3-D Parachute Simulation by the Immersed Boundary Method[J]. Computers & Fluid, 2009, 38(6): 1080-1090.

[19] MIYOSHI M, ISHII T, HASHIMOTO A, et al. Computational Analysis of Parachute Motion Using the Immersed Boundary Method[C]//46th AIAA Aerospace Science Meeting and Exhibit, AIAA Paper 2008-311, Reno, Nevada, 2008.

[20] XUE X, KOYAMA H, NAKAMURA Y, et al. Effects of Suspension Line on Flow Field around a Supersonic Parachute[J]. Aerospace Science and Technology, 2015, 43: 63-70.

[21] XUE X, KOYAMA H, NAKAMURA Y. Numerical Simulation of Supersonic Aerodynamic Interaction of Aparachute System[J]. Trans. JSASS Aerospace Tech. Japan, 2013, 11: 33-42.

[22] NISHIYAMA Y. Aerodynamic Characteristics of the Supersonic Parachute with Its Opening Process[D]. Nagoya: Master Thesis of Nagoya University, 2013.

[23] SHIMA E, JOUNOUCHI T. Roe of CFD in Aeronautical Engineering (No.14) -AUSM type Upwind Schemes-[C]// Proceedings of 14th NAL Symposium on Aircraft Computational Aerodynamics, NAL-SP-34, Special publication of National Aerospace Laboratory, 1997: 7-12.

[24] OCHI A, NAKAMURA Y. A Development of Aerodynamics Analysis Tool Using Cartesian System (First Report)[C]//The Japan Society of Fluid Mechanics 19th CFD symposium, 2005.

[25] PESKIN C S. Flow Patterns Around Heart Valves: a Numerical Method [J]. Journal of Computational Physics, 1972, 10(2): 252-271.

[26] BAMHARDT M, DRAYNAT T, et al. Detached Eddy Simulations of the MSL Parachute at Supersonic Conditions[C]//19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, AIAA Paper 2007-2529, Williamsburg, VA, 2007.

[27] El-GENDI M. Effect of Trailing Edge Geometry on the Flow Behavior through Rectilinear Turbine Cascades[D]. Nagoya: Doctor Thesis of Nagoya University, 2010.

[28] BENNEY R J, STEIN K R. Computation Fluid-structure Interaction Model for Parachute Inflation[J]. Journal of Aircraft 1996, 33(4): 730-736.

Numerical Simulation of Aerodynamic Interaction of Supersonic Parachute System

XUE Xiaopeng1WEN Chihyung2

(1 School of Aeronautics and Astronautics, Central South University, Changsha 410084, China)(2 Shenzhen Research Institute, The Hong Kong Polytechnic University, Shenzhen 518057, China)

In the present study, the supersonic flow over a three-dimensional flexible parachute system is numerically simulated by using a simple “immersed boundary technique” together with the fluid-structure coupling scheme. The parachute system employed here consists of a capsule and a canopy. The objective of this study is to investigate the effects of aerodynamic interaction on the dynamics of the canopy behavior, to clarify the performance of the supersonic parachute system in terms of design parameters such as trailing distance between the capsule and canopy, and furthermore to confirm whether “Detached Eddy Simulation”（DES）method can be applied to solve the supersonic flexible three-dimensional parachute problem. As a result, as the trailing distance is rather small, the canopy undergoes severe shrink. As this distance increases, the area oscillation of the canopy shape is observed, leading to a larger drag coefficient. Moreover, when Detached Eddy Simulation method is applied in the case with larger trailing distance, the capsule turbulent wake interacts with the canopy shock more strongly, leading to a larger drag coefficient.

aerodynamic interaction; detached eddy simulation; fluid-structure interaction; supersonic parachute

（编辑：陈艳霞）

V445

A

1009-8518(2016)03-0009-10

10.3969/j.issn.1009-8518.2016.03.002

薛晓鹏，男，1982年生，2009年获日本名古屋大学航空航天工程专业博士学位，现任中南大学航空航天学院讲师。研究方向为气动力减速器技术数值计算方法。E-mail：xuexiaopeng@csu.edu.cn。

温志湧，男，1964年生，1994年获美国加州理工学院航天博士学位，现任香港理工大学机械工程系深圳研究院教授。主要研究方向为高超空气动力学，实验流体力学，智能流体。

2015-09-23