BP神经网络算法的技术分析

张 东

（郑州升达经贸管理学院，河南 郑州 451191）

BP神经网络算法的技术分析

张 东

（郑州升达经贸管理学院，河南 郑州 451191）

本研究通过对BP神经网络的特点及其原理进行简单介绍，提出当前的一些算法改进，分析各种算法的优缺点，最后对BP神经的应用现状进行了探讨。

人工神经网络；BP算法；优化算法；最佳预测

本文著录格式：张东.BP神经网络算法的技术分析[J].软件，2016，37（12）：227-229

0 前言

BP神经网络又称人工神经网络，它是一种模拟动物神经网络的数学模型。神经网络是在现代生物学研究人脑组织成果的基础上提出的，用来模拟人类大脑神经网络的结构和行为。神经网络反映了人脑功能的基本特征，如并行信息的处理、学习、想象、记忆等。BP神经网络是由人工神经元互连组成的网络，以人工神经元为节点，用有向加权弧连接起来的有向图，其中人工神经元模拟人脑神经元，有向弧模拟轴突—突触—树突对，有向弧的权值表示相互连接的两个人工神经元相互作用的强弱。

1 BP神经网络的基本原理

早在1986年首先由Romelhart和Mc2clelland提出误差反向传播算法（Error Back Propagation Algorit hm，简称BP算法），由于在应用中误差反向传播算法常用于多层前反馈网络的训练，也常把多层反馈网络成为BP网络[1]。

BP网络模型包括其输入输出模型、作用函数模型、误差计算模型和自学习模型。

1.1 节点输出模型

f-非线形作用函数，q-神经单元阈值。

图一 BP神经网络的典型结构

1.2 作用函数模型

作用函数是反映下层输入对上层节点刺激脉冲强度的函数又称刺激函数，一般取为(0,1)内连续取值Sigmoid函数f(x)=1/(1+e-x)

1.3 误差计算模型

误差计算模型是反映神经网络期望输出与计算输出之间误差大小的函数：

Ep=1/2×∑(tpi-Opi)2 tpi-i节点的期望输出值；Opi-i节点计算输出值。

1.4 自学习模型

神经网络的学习过程，即连接下层节点和上层节点之间的权重拒阵Wij的设定和误差修正过程。BP网络有师学习方式-需要设定期望值和无师学习方式-只需输入模式之分。自学习模型为△Wij(n+1)= h ×Фi ×Oj+a×△Wij(n) h-学习因子；Фi-输出节点i的计算误差；Oj-输出节点j的计算输出；a-动量因子。

2 目前BP神经网络算法存在的问题及改进措施

2.1 BP神经网络算法存在的问题

①容易陷入局部极小，使得全局达不到最优；

②训练次数过多，误差下降缓慢，影响收敛速度，使得学习效率低下；

③选取隐节点是缺乏理论指导。当隐节点过多时，使得网络学习的时间变长，甚至会发生不能收敛的情况；当隐节点过少时，网络的容错力较差；

④训练时会发生学习新样本忘记旧样本的情况。

2.2 BP神经网络算法的改进措施

针对BP网络算法易出现的问题，国内外的学者教授对此进行了深入细致的研究，并提出了一些改进措施：

2.2.1 新增动量项。这种方法也可以称为惯性校正法，可以用下面的权值调整公式表示：

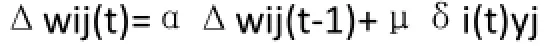
μδi(t)yj表示BP神经网络算法的修正量，其中δi(t)为广义误差，yj为神经元在第j层的输出；Δ wij(t-1)为动量项，α是动量系数。在使用加入动量项这一方法后，可以加快收敛的速度并抑制振荡。在何玉彬，李新忠所著《神经网络技术及其应用》中对这一方法做了更加深入的研究和推广[2]，在该研究中涉及的增广LPIDBP学习算法，就是通过对微分、积分、误差梯度的比例进行组合，从而形成调节量。

2.2.2 改变学习率。在BP神经网络中，学习率又可称为步长，BP算法中学习率设定成常数，但在实际应用时，无法确定最佳的学习率。通过观察误差曲面，在平坦区域内，学习率过小会使得训练次数增加，此时提高学习率的作用就十分重要；在误差变化剧烈的区域，学习率过大会导致调整量过大，跨过较窄的坑凹处，整个训练会由于出现震荡使得迭代次数的增加[3]。在不同的区域内过大过小的学习率都会对收敛过程产生不利影响，而进行学习率的自使用改变，让学习率在改增大的时候增大，在该减小时较小，可以很容易的避免收敛过程过慢的情况。

2.2.3 采用其他梯度优化算法。最速下降梯度法自身的特点决定了BP算法收敛速度慢的缺点，最速下降可以使得初期的迭代速度很快接近于极值点[4]，但最终收敛仍需较长时间。因此可以采用拟牛顿法共轭梯度法、Levenberg-Marquardt法克服这一缺点。这些算法的共同特点是二阶学习算法，当误差曲面接近于极值点附近时，具有很快的收敛速度。

2.2.3.1 拟牛顿法。拟牛顿法在搜索方向下比传统方法有所改进，它可以利用准则函数在搜索上的梯度，并且使用了二次倒数，更好的利用了搜索点提供的信息，使得搜索方向更加精准的指向最优点。它的迭代方程可以表示为：Δw（k+1）=w（k）-D-1▽f（w（k））

拟牛顿法的收敛速度快于一阶梯度，但缺点是计算过程较为复杂，典型的算法有一步正切拟牛顿法、BFGS拟牛顿法[5]。在进行应用时MATLAB中的工具函数trainbfg（）、trainoss（）即对应拟牛顿法中的BFGS拟牛顿法和一步正切拟牛顿法

2.2.3.2 共轭梯度法。传统算法收敛速度慢，拟牛顿法计算较为复杂，但共轭梯度法可以很好的规避以上两种缺点。共轭梯度法是一种通过改进搜索方向的方法，把计算中前一步骤的梯度乘上适当的系数，加上该点的梯度，可以得到新的搜索方向。它的迭代方程可以表示为：Δw（k+1）=w（k）+ρ（k）S（k） ρ（k）为最佳步长

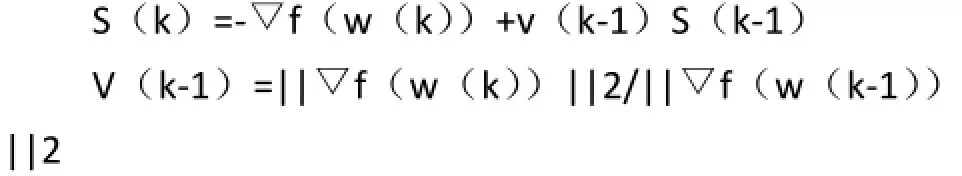
共轭梯度法比大多常规的梯度下降法收敛速度更快，且只需要增加有限的存储量和计算量[6]。当进行权值较多的神经网络计算时，尤其适用共轭梯度法。在实际应用时MATLABz中的traincgb（）、traincgf（）、traincgp（）工具函数即为共轭梯度法。

2.2.3.3 Levenberg-Marquardt法。Levenberg-Marquardt法其实是传统算法和牛顿法的结合体，它具有在权值数较少是比传统算法和其他改进算法的迭代次数少，收敛速度快，精确度高等优点。但由于该算法较为复杂，运用时会占用大量的内存空间，花费更多的计算时间。在应用时MATLAB中的teainlm（）工具函数即为Levenberg-Marquardt法的改进算法。

2.2.4 结合遗传算法和退火算法。立足于目前网络算法的利用情况，遗传算法和模拟退火算法作为典型研究对象，相关学者对其研究程度也最为深入，偏向于采用数值优化的方法，泛化性能较为完善且局部极小值相对稳定[7]。基于此，限于篇幅内容，本研究仅对遗传算法和模拟退火法进行探讨。

①遗传算法（GA）。基于BP神经网络算法改进，遗传算法具备模拟自然进化机制的特点，与进化策略、进化规划等方面具有一定联系[8]。其中，应用最广的遗传算法有两个明显的特点，即群体搜索策略和群体与个体信息交换。以参数编码、设定初始群体、设计适应度函数、设计遗传操作（选择、交叉、变异）、设计控制参数为遗传算法的核心五要素，确定BP网络的结构权值、阀值选定程序。并且，遗传操作中的交叉和变异是算法优化的关键步骤，交叉保证子代对父代优良特点的继承，变异则为群体的多样性提供了可能，较易跳出局部极值（满足评价个体适应度）。

文献6是利用遗传算法对神经网络优化的步骤做了详细阐述。文献7对遗传算法进行了权值优化的仿真实验，以证明其精度、效率、简易型均优于传统算法。此外文献8遗传算法在优化权值和优化网络结构上做了有益的探索[9]，该算法中五要素的仍有较大的设计随意性，导致算法的成功与否还得依靠算法设计人员的经验和反复耐心的操作。

②模拟退火算法（SA）。由于该种算法有金属的物理退火具有一定的相似性，因而得此名称。模拟退火法是通过利用Metropolis抽样中的概率突跳特点进行随机搜索，随着温度的下降，抽样不断重复，直到最终得到最优解。通过马氏链可以得出：初始温度足够高，温度下降足够慢的情况下，SA是收敛的。模拟退火算法可有效避免局部极小值，达到全局优化功效，正由于这一特点使得该算法过程时间较长。文献9对比了遗传算法和模拟退火法，得出了模拟退火法比传统算法更好，但由于模拟退火法是点对点搜索的优化，许多算法参数选择困难，其总体性能不如遗传算法。

3 BP神经网络算法的应用

结合BP神经网络算法的实际问题，重点论述最优预测的应用案例，联系实践生产活动以达到BP神经网络预测方法的优化目标。在日常实践活动中，通过BP神经网络建立模拟人脑活动的模型，使其具有大规模处理信息的能力、自训练学习能力等，可以用于舆情预测、销售预测、股市预测等。并且，在BP神经网络应用实际生活生产前，由网络舆情危机构成的预警研究也已构成雏形，结合BP神经网路算法应用机制，构建科学、系统、可行的预警指标体系对其具备防范功效，转入非线性关系演算程序，打破局部最小值误区（选择全局搜索、优化算法），从而具有样本记忆和联想的能力。以2015年中期河南省文化类网络舆情相关事件为例，整合媒体分析内容，以教育、文脉、媒体三个关键词作为此次突发事件的典型代表，利用BP神经网络算法进行具体分析[10]。在此期间，经由网络预测的实际训练，依据网络舆情危机等级与网络舆情传播阶段结合趋势，明确优化BP神经网络的初始权值及阀值，结合MATLAB工具箱、预警模型所占据的数据比例，转用BP神经网络预测方法的精度效应，便于缩减预测结果的真实数值偏离程度，具备较强的适用性[11]。

4 结语

BP神经网络算法可对社会生产生活进行预测监控和图像压缩编码过程等，但BP神经网络固有的最速下降梯度机制[12]，导致其收敛速度慢，存在局部极小等问题。在实际生活中，明确BP神经网络的基本原理，依据原有的实际问题，从新增动量项、改变学习率、采用其他梯度优化算法、结合遗传算法和退火算法等方面入手探究改进优化举措[13]，使改进后的算法更加适用于生产生活中。此外，BP神经网络算法已在实际生活中有所应用，尤以网络舆情危机演示为典型特征，希望本研究对BP神经网络算法的研究发展有所裨益。

[1] 刘载文,等.过程神经元网络学习算法及软测量方法的研究[J].系统仿真学报,2007,19(70):1456-1459.

[2] 王益群,等.神经网络软测量模型中全共轭梯度算法研究[J].机械工程学报,2005,41(6):97-101.

[3] 钟珞,饶文碧,邹承明.人工神经网络及其融合应用技术[M].北京:科学出版社,2007.

[4] 郭敬,董彦良,赵克定.基于混合优化策略的自回归—滑动平均模型建模[J].机械工程学报,2007,43(4):229-233.

[5] 候祥林,等.多层人工神经网络合理结构的确定方法[J].东北大学学报(自然科学版),2003,24(1):35-38.

[6] 王益群,等.基于基于神经网络的热轧带钢卷取温度预报[J].中国机械工程,2005,16(11):990-992.

[7] Randall S.Sexton,Robert E.Dosey,John D.Johnson.To-ward global optimization of network:A comparison of the ge-netic algorithm and back propagation.Decision Support Sys-tems,1998.22:171～185

[8] Randall S.Sexton,JatinderN.D.Gupta.Comparative eval-uation of genetic algorithm and back propagation for trainingneural networks.Information Sciences,2000.129:45～59

[9] Randall S.Sexton,Robert E.Dorsey,John D.Johnson.Optimization of neural networks:A comparative analysis ofthe genetic algorithm and simulated annealing. European Journal of Operational Research,1999.114:589～601

[10] Wang S, Liu Z, Sun Q, Zou H, Yang F. Towards an accurate evaluation of quality of cloud service in service-oriented cloud computing. Journal of Intelligent Manufacturing,2014,25(2):283-291.

[11] 张 雁，王 棵，刘玉连，等. 基于微信平台的计算机专业学习通[J]. 软件，2016，37（4）：115-118

[12] 胡 健，王理江. 数据挖掘在选课推荐中的研究[J]. 软件，2016，37（4）：119-121

[13] 邹积凯. 公安系统应急平台建设及资源应用研究[J]. 软件，2016，37（4）：122-125

Technical Analysis of BP Neural Network Algorithm

Zhang Dong

（Zhengzhou Shengda Economics and Trade Management College, Zhengzhou,Henan 451191）

This study through the BP neural network and the characteristics of the principle of a simple introduction,some of the current algorithm to improve the analysis of the advantages and disadvantages of various algorithms, and finally the application of the BP nerve was discussed.

artificial neural network; BP algorithm; optimization algorithm; the best prediction

TP183

A

10.3969/j.issn.1003-6970.2016.12.049

张东（1988—），男，河南郑州人，助教、网络工程师，郑州升达经贸管理学院教师，研究方向：计算机网络安全及算法分析。