SINS/陆基单站组合导航系统建模与性能仿真验证

王 勋，王新龙，车 欢，张金鹏

(1.北京航空航天大学 宇航学院，北京 100191; 2.航天恒星科技有限公司，北京 100086; 3.中国空空导弹研究院，河南 洛阳 471009)

SINS/陆基单站组合导航系统建模与性能仿真验证

王 勋1，王新龙1，车 欢2，张金鹏3

(1.北京航空航天大学 宇航学院，北京 100191; 2.航天恒星科技有限公司，北京 100086; 3.中国空空导弹研究院，河南 洛阳 471009)

针对弹道导弹的特点，在分析陆基单站定位原理的基础上，详细建立了单站定位的误差模型，并设计了两种可行的SINS/陆基单站组合导航系统方案：松组合导航系统和紧组合导航系统。通过仿真对比，紧组合导航系统收敛性好、导航精度高，能够很好地抑制惯导系统误差积累现象，有较高的导航性能。

陆基单站； 捷联惯导； 弹道导弹； 组合导航

0 引 言

惯性导航系统(Inertial Navigation System，INS)是一种自主性强、高动态、隐蔽性好且高精度的导航系统，但其最大的缺陷是导航误差随时间

积累[1-3]，因此需要利用其他设备作为参考信息源，定期对惯性导航输出进行综合校正和对惯性器件漂移进行补偿。陆基导航系统(Land-Based Navigation System，LNS)借助于运动载体上的电子设备接收陆基导航站的无线电信号，通过处理获得的信号来获得导航参量，从而确定载体位置[4]。该系统的主要优点[5]如下：(1)不受时间、天候的限制； (2)测量定位数据更新率高，甚至可以连续地、实时地定位； (3)定位精度不随时间漂移； (4)地面站采用大功率发射机，并配备有完善的地面监测站，具有极高的可靠性； (5)用户设备简单、价格低廉。陆基单站定位是利用一个陆基导航站对载体进行定位，由于其具有高度的独立性以及无需进行复杂的时间同步等优点而引人瞩目。

当前，单一的导航手段很难满足现代战争对高精度、高可靠性、自主、隐蔽、抗干扰、全球、全天候导航保障能力的要求[6-7]。因此，采用组合导航系统将成为导航技术发展的必然趋势。

SINS/陆基组合导航是以捷联惯导系统为主，将陆基导航作为辅助导航手段，通过数据融合技术对SINS进行实时校正，以达到较高的导航精度。这种系统利用惯导系统和陆导系统各自的优点，进行系统间的取长补短，有效减小系统误差，提高系统精度，同时还可以降低导航系统的成本。

本文设计了一种适用于弹道导弹的SINS/陆基组合导航系统方案，并对其两种组合模式的性能进行了对比。

1 陆基单站系统定位模型

根据AOA/TOA定位原理，测距系统和测角系统的地面设备同址安装，载体获得其相对于地面站的距离、磁方位角参量，确定出一条圆位置线和直线，其交点就是载体在二维平面内的位置[8-10]，拓展至三维空间，陆基单站的三维空间定位模型如图1所示。

图1 三维空间定位示意图

在OXYZ坐标系中，设地面站P的坐标为(x0,y0,z0)，载体M的坐标为(x,y,z)，载体相对于地面站的磁方位角为α、斜距为r、仰角为θ； 载体的当地高度为H。则根据几何关系可以列出如下定位方程组：

(1)

式中：磁方位角α、斜距r可分别通过测角、测距系统获得； 载体的当地高度H由高度计测量得到。

求解定位方程组, 即可得到三维空间中载体的位置：

(2)

由此可见，载体利用测距、测角系统获得的磁方位角和斜距信息，附加以高度计测量得到的信息，即可确定载体在三维空间中的位置。

2 单站定位系统误差分析与建模

考虑到载体利用地面站的距离一般不超过400 km，除去在高纬度地区外，东北天地理坐标系相对于载体所在的基准台坐标系之间所转过的角度是小角度，位置和角度矢量在地理坐标系与基准台坐标系上各分量差异很小，可以忽略。因此，在推导三维空间中的定位误差公式时，可以忽略地球表面的曲率，假设地理坐标系与基准台坐标系相平行。

(3)

对式(3)在(r, H, α)处进行一阶泰勒展开，并移项整理可得

(4)

X=AL

(5)

则定位误差的协方差矩阵为

E[XXT]=AE[LLT]AT

(6)

若Δα，Δr和ΔH三者相互独立，并令σr，σH，σα分别为磁方位角、斜距及高度三个观测量的误差标准差，则可得协方差阵：

(7)

令σxx，σyy，σzz分别为x，y，z三个方向的位置误差标准差，σxy，σyz，σxz分别为耦合误差标准差，将式(7)和矩阵A代入式(6)可得

(8)

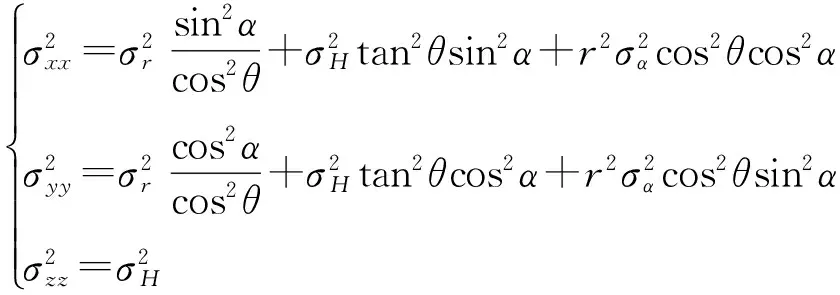
(9)

由定位误差公式(9)可以看出，陆基单站系统的定位误差与以下两个因素有关：

(1) 测量因素。其反映了系统的测量误差影响，其中σα，σr，σH直接反映磁方位角α、斜距r及高度H的测量误差。根据公式(9)，x和y方向的定位误差与磁方位角α、斜距r及高度H的测量误差均有关，而z方向的定位误差只与高度测量误差有关。

(2) 几何因素。其反映了载体和地面站的相对几何位置关系对定位误差的影响。由公式(9)可以看出，x和y方向的定位误差与磁方位角α、斜距r及俯仰角θ的大小均有关，而z方向定位误差与地面站的布局无关。

3 SINS/陆基单站组合模式

3.1 组合导航系统结构

3.1.1 松组合导航系统

松组合是一种基于SINS和陆基导航系统测得的位置信息进行导航定位的方法[11]。其采用的量测信息是位置信息，利用陆基导航子系统计算得到位置，与SINS解算的位置之差作为卡尔曼滤波器的输入，将估计误差反馈至SINS进行校正。松组合系统的结构框如图2所示。

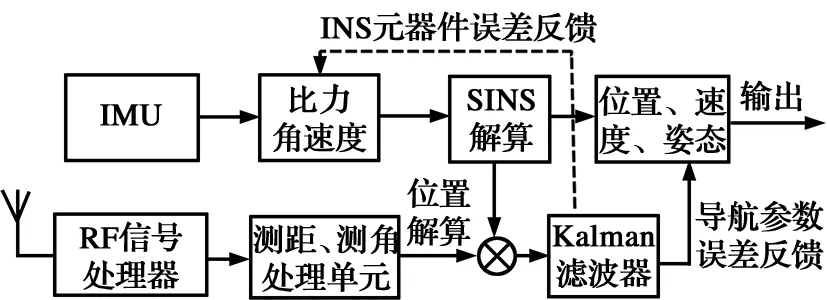
图2 松组合导航系统结构框图

3.1.2 紧组合导航系统

紧组合是一种相对复杂的组合方式，其采用磁方位角、斜距的组合模式，原理如图3所示。根据SINS信息和从陆基应答信号中提取的信息，计算导弹相对于陆基站的方位角和斜距，并与测距、测角系统获得的磁方位角和斜距相减作为Kalman滤波器的量测信息，然后利用滤波器估计SINS的位置误差量，最后对SINS输出或反馈校正。

紧组合模式中，将测距、测角系统与SINS耦合，可使用估值信息来重置SINS的参数。该模式采用原始的磁方位角和斜距测量值直接送入组合滤波器，具有较好的可观测性。

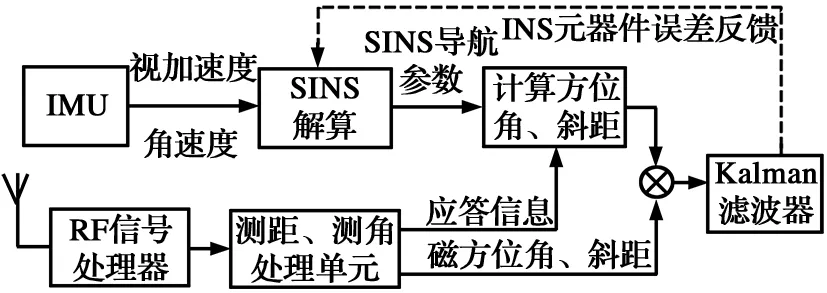
图3 紧组合导航系统结构框图

3.2 系统状态方程和量测方程

3.2.1 组合系统状态方程

在SINS/陆基组合导航系统中，SINS是整个组合导航系统的基本参考系统。组合导航系统以惯导的误差方程为主状态方程，同时可按IMU和行状态扩充。而对基于询问-应答模式的陆基导航系统，信号收发均使用同一接收机时钟，接收机钟差对测距影响较小，可将其视为高斯白噪声[12]。

考虑到陆基单站导航系统涉及到方位角的测量，为了便于分析，可选择东北天地理坐标系作为基准坐标系建立滤波数学模型。SINS/陆基单站组合导航系统状态方程可写成如下形式：

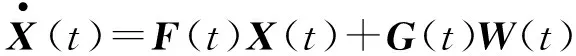
(10)

式中：X(t)为系统状态向量；W(t)为系统噪声向量；F(t)为系统矩阵；G(t)为系统噪声矩阵。

状态向量为

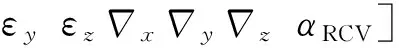
(11)

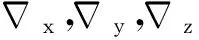
系统噪声阵为

W(t)=[wgx,wgy,wgz,wax,way,waz]T

(12)

式中:wgx,wgy,wgz为陀螺仪随机噪声；wax,way,waz为加速度计随机噪声。

3.2.2 松组合系统量测方程

SINS/陆基松组合系统采用SINS解算的位置与陆基导航系统计算得到的位置之差作为量测信息。

在东北天地理坐标系中，设载体的真实位置为(x,y,z)； SINS解算的载体位置为(xINS，yINS，zINS)； 陆基导航系统计算的载体位置为(xS，yS，zS)。将SINS解算的位置信息与陆基导航系统测得的位置信息作差，并将位置之差转换至大地坐标系中，可得到松组合系统的位置量测方程为

(13)

将上式写成矩阵形式为

Zc=HcX+Vc

(14)

(15)

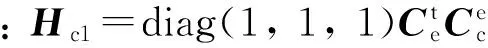
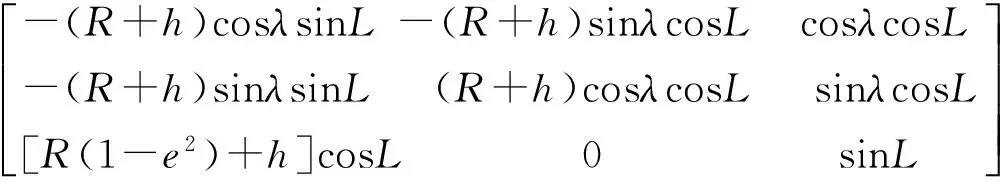
3.2.3 紧组合系统量测方程

(1) 斜距量测方程

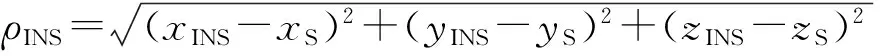
(16)

载体真实位置至陆基站P的斜距r为

(17)

将式(16)在(x,y,z)处进行泰勒级数展开，并取一次项误差，可得

(18)

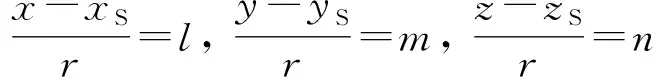
ρINS=r+lδx+mδy+nδz

(19)

载体上的测距系统测得的斜距可表示为

ρS=r+vρ

(20)

对式(19)和式(20)作差，便可得斜距差的矩阵形式为

(21)

将式(21)中的位置误差先从地理系转换到地心地固系，然后再转换到大地系中。

地心地固系和大地坐标系之间的转换关系为

(22)

对式(22)中各等式两边取微分，可得

(23)

将式(23)代入式(21)，整理得到斜距差量测方程为

Zρ=HρX+Vρ

(24)

(25)

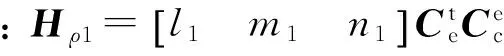
(2) 磁方位角量测方程

在东北天地理坐标系中，设载体的真实位置为(x,y,z)； SINS推算得到的载体位置为(xINS,yINS,zINS)； 陆基单站的精确位置为(xS,yS,zS); 磁方位角为αS，定义为载体位置至陆基站连线与极北方向的夹角，并设顺时针为正。则由SINS推算的载体相对于陆基站的方位角αINS为

αINS=arctan[xINS-xS/yINS-yS]

(26)

载体的真实位置相对于陆基站P的方位角α为

α=arctan[x-xS/y-yS]

(27)

将式(27)在(x,y,z)处进行泰勒级数展开，并取一次项误差可得

(28)

式中：R=(x-xS)2+(y-yS)2。

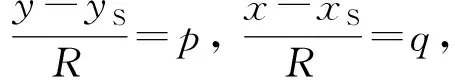
αINS=α+pδx-qδy+0·δz

(29)

载体上的测角设备测得的磁方位角αS可以表示为

αS=α+vα

(30)

则方位角差量测方程可表示为

(31)

与斜距的情况类似，需要将地理系下的位置误差先转换到地心地固系，然后再转换到大地系(λ,L,h)中，则磁方位角量测方程为

Zα=HαX+Vα

(32)

(33)

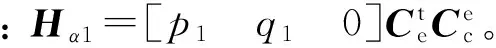
4 仿真验证

4.1 仿真条件设定

(1) 惯性元件仿真参数

初始对准误差：方位失准角误差为10′(3σ)，水平调平误差为2′(3σ)；

陀螺仪：常值漂移误差为0.03(°)/h(3σ)，各个方向安装偏差均为15″(3σ)，驱动白噪声均方差为0.02(°)/h；

加速度计：零偏稳定性为5×10-5g(3σ)，标度因数稳定性为5×10-5(3σ)，驱动白噪声均方差为10-5g；

数据输出频率：惯性器件的数据输出频率为100 Hz。

(2) 陆基系统仿真参数

测距系统：测距接收机标准偏差为20 m(1σ)，测距应答站标准差为20 m(1σ)，总体均方差为28.3 m(1σ)；

测角系统：测角接收机标准偏差为0.015°(1σ)，测角发射台标准偏差为0.015°(1σ)，总体均方差为0.021°(1σ)；

数据输出频率：陆基导航器件的数据更新率为15 Hz。

(3) 高度计仿真参数

采用的雷达高度计的误差均方差为10 m(3σ)。

4.2 仿真验证平台的设计

首先设计导弹仿真弹道，如图4所示。发射点坐标为(116.0°E，40.0°N)，向正东发射，发射仰角为90°(垂直发射)，射程为2 217.0 km，弹道顶点高度为371.4 km，飞行时间为658.6 s。前20 s为垂直上升段，60 s主动段转弯结束，160 s发动机关机，658 s导弹落地，落地坐标为(141.2°E，40.0°N)。陆基导航系统工作段设定在导弹上升段，工作时间为发射后62～150 s，即组合导航工作时段。

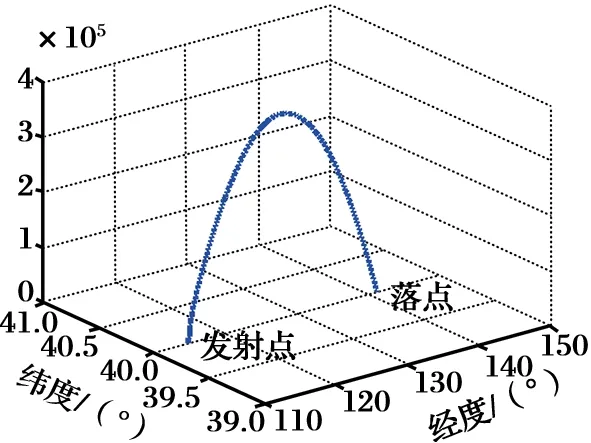
图4 弹道导弹仿真轨迹

在上述仿真条件下，SINS系统单独工作时的位置误差如图5所示。

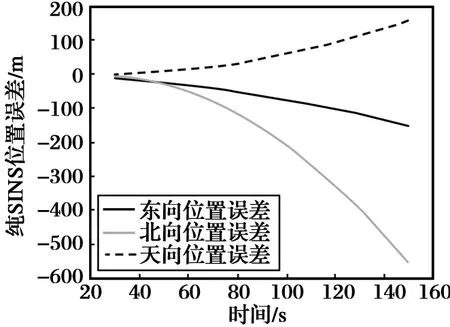
图5 纯SINS位置误差

图5中，在初始设定的加速度计、陀螺仪误差模型和初始对准误差的条件下，由于惯性元件(加速度计、陀螺仪)的误差以及惯导系统自身的误差发散特性，SINS单独工作时，位置误差有随时间增加逐渐积累的趋势。根据仿真数据，在上升段范围内北向位置误差较大，约为-550 m，东向位置误差约为-150 m，天向位置误差约为180 m。

4.3 导航性能仿真与分析

根据仿真条件，在陆基导航系统正常工作时，分别得到紧组合和松组合系统的仿真结果。图6～8分别为紧组合与松组合系统位置误差对比结果，表1为仿真结果对比。

通过将图6～8的组合导航系统的位置误差与图5进行对比可以看出，由于陆基导航系统能够提供斜距和磁方位角等观测信息，这两个观测量均不包含随时间积累的误差，利用卡尔曼滤波对载体的位置误差进行估计，并将估计值反馈至SINS进行校正，因而，组合导航系统与纯SINS工作时相比，误差更小。由图6～8可见，东向位置误差从150 m下降为4.7 m，北向位置误差从550 m下降为5.2 m，天向位置误差从180 m下降为4.8 m。可见，组合系统的导航精度得到了大幅提高。

此外，由表1及图6～8还可以看出，紧组合比松组合系统收敛速度更快，位置误差更小。紧组合系统是利用原始信息(斜距和磁方位角)进行滤波估计，观测信息实时性强，且这两种信息及其噪声不相关，提高了滤波器的随机可观性，进而提高其误差估计精度。松组合采用的量测信息是斜距和磁方位角计算得到的位置，不仅包含了斜距和磁方位角的误差，还引入了计算误差和数据延迟，致使观测噪声出现时间相关性，滤波器便将信息中的时间相关部分归因于状态，从而破坏状态估计，增大估计误差。根据仿真数据，紧组合系统的东北天位置误差均值分别为-0.27 m，-0.38 m和-0.90 m，误差标准差分别为2.30 m，2.00 m和1.49 m，误差较为稳定； 而松组合系统的导航误差波动幅度较大，东北天位置误差标准差分别为4.61 m，4.02 m和3.35 m，导航性能明显不及紧组合系统。

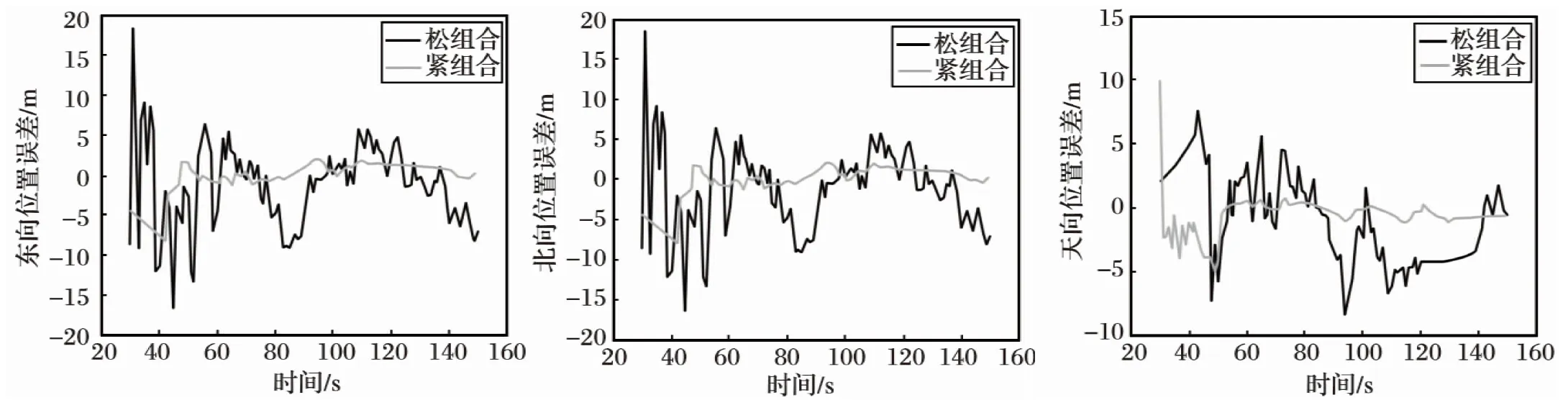
图6 东向位置误差 图7 北向位置误差 图8 天向位置误差

表1 松组合与紧组合仿真结果对比

5 结 论

通过对基于测角、测距的陆基单站系统的分析和建模，分别建立了SINS/陆基单站紧组合和松组合导航系统模型，并进行了仿真验证。仿真结果表明，松组合系统引入计算误差和数据延迟，致使观测噪声出现时间相关性，破坏状态估计，估计误差较大。而紧组合导航系统充分利用各子系统的实时信息，能够较好地抑制惯导系统误差发散现象，导航精度高、收敛速度快，能够满足弹道导弹对导航系统性能的要求。

[1] Misra P, Enge P. Global Positioning System: Signals, Measurements and Performance[M]. 2nd ed. Lincoln, MA: Ganga-Jamuna Press, 2006.

[2] 严建华. 建立我国陆基定位、导航、授时系统研究[J]. 导航, 2009, 45(1): 1-4.

[3] 郝燕玲, 陈实如, 徐定杰. 陆基增强/双星定位组合系统[J]. 哈尔滨工程大学学报, 2002, 23(1): 47-51.

[4] 王丹丹, 王小军, 陈小军, 等. 陆基导航三站定位与四站定位 Pdop 值分析[J]. 航天控制, 2009 (5): 15-19.

[5] Kintner P M, Ledvina B M. The Ionosphere, Radio Navigation, and Global Navigation Satellite Systems[J].Advances in Space Research, 2005, 35(5): 788-811.

[6] 刘楠, 杨莘元, 姜弢. 多用户检测在陆基无线电导航系统中的应用[J]. 系统工程与电子技术, 2007, 29(6): 870-873.

[7] 牛磊, 董浩. 扩展卡尔曼滤波在陆基无线电导航系统定位解算中的应用[J]. 应用科技, 2004, 31(8): 47-49.

[8] 陈实如, 孙尧. 基于陆基增强系统提高双星定位精度的研究[J]. 导航, 2002, 38(1): 15-22.

[9] 朱学勇, 柴俊栓. 利用陆基无线电测距信息修正惯导技术研究[J]. 现代电子技术, 2009, 32(13): 152-154.

[10] 施健. 满足区域导航性能的陆基导航技术研究 [D]. 南京: 南京航空航天大学, 2010.

[11] Harlin W J, Cicci D A. Ballistic Missile Trajectory Prediction Using a State Transition Matrix[J]. Applied Mathematics and Computation, 2007, 188(2): 1832-1847.

[12] Dardari D, Falletti E, Luise M. Satellite and Terrestrial Radio Positioning Techniques: A Signal Processing Perspective[M]. Academic Press, 2011.

Simulation and Validation of SINS/Land-Based Single Station Integrated Navigation System

Wang Xun1, Wang Xinlong1, Che Huan2, Zhang Jinpeng3

(1. School of Astronautics，Beihang University，Beijing 100191，China; 2. Space Star Technology Co.，Ltd，Beijing 100086，China; 3. China Airborne Missile Academy，Luoyang 471009，China)

According to the characteristics of ballistic missile, based on the analysis of land-based single station positioning system, the error model of single station location system is established in detail, and two kinds of SINS/land-based single station schemes with regard to integrated navigation system are designed, which are loosely integrated navigation system and tightly integrated navigation system. The simulation results show that the tightly integrated navigation system has good convergence and navigation precision, and can restrain the error accumulation of inertial navigation system with better navigation performance.

land-based single station; SINS; ballistic missile; integrated navigation

10.19297/j.cnki.41-1228/tj.2016.06.012

2015-10-29

航空科学基金项目(20130151004； 2015ZC51038)； 卫星应用研究院创新基金项目(2014_CXJJ-DH_01)

王勋(1990-)，男，山东菏泽人，硕士研究生，研究方向为惯性导航、陆基导航以及组合导航。

V241

A

1673-5048(2016)06-0055-06