一种基于新型动态混合重叠网格的数值模拟方法

刘 超，刘仙名，王立强

(中国空空导弹研究院，河南 洛阳 471009)

一种基于新型动态混合重叠网格的数值模拟方法

刘 超，刘仙名，王立强

(中国空空导弹研究院，河南 洛阳 471009)

外挂导弹发射时导弹处于载机复杂干扰流场中，会导致空气动力的非定常、非线性特性。此时运用常规风洞实验数据插值作为工程气动数据基础在一定程度上存在误差。本文提出一种基于计算流体力学(CFD)的非定常数值模拟方法，将飞行力学方程与空气动力学方程耦合求解，更精确地模拟真实的飞行状态。所采用的新型动态混合重叠网格相比于以往重叠网格具有生成简便、针对运动过程可自适应调整等优点。以标准投弹算例作为验证算例，结果体现了本文网格和数值模拟方法的工程应用价值。

动态混合重叠网格； 非定常； 网格动态自适应； 三线性插值； 六自由度

0 引 言

现代战斗机的外挂导弹武器，在发射初始阶段对载机的安全性有重要影响。发射导弹时，导弹处于载机复杂干扰流场中，会出现空气动力的非定常、非线性甚至非对称特性，引起气动和运动的交叉耦合[1]，此时往往出现非正常分离，如若导弹与载机发生碰撞，则会严重威胁载机与飞行人员安全。导弹气动设计师必须对外挂导弹发射时的气动特性加以研究，以确保发射条件不受太大影响，保证载机安全。世界各航空大国均投入大量人力和物力，从计算和实验两方面研究多体干扰及多体分离问题。此外，为了有效击中目标，需要掌握投放初始阶段导弹姿态和运动轨迹数据。因此，对导弹与载机分离进行数值模拟，研究导弹发射过程中的机弹气动力干扰，考虑其对导弹发射后初始弹道的影响十分必要。

由一般风洞实验和计算流体力学(Computational Fluid Dynamics，CFD)方法得到的局部线性化气动力数据，在运动状态较为复杂的情况下不能准确描述飞行器的非定常、非线性气动力和运动规律。随着CFD方法的发展，综合运用空气动力学、飞行力学耦合一体化数值模拟技术是研究和解决这类问题的一个新途径。其特殊的研究方式，也能在一定程度上填补静态风洞实验数据以及静态CFD计算数据和飞行实验之间的数据空白[2]。

重叠网格(overlapping grids)也叫Chimera网格[3]或者嵌套网格(overset grids)，该类网格的实质是一种网格的区域分割和组合策略[4]，其主要优点是降低了网格生成的难度，提高了网格生成的灵活性，保证了原始网格的质量等。而重叠网格方法特别适用于复杂外形和多体相对运动，特别是20世纪90年代以来，动态重叠网格技术的提出和发展[5-6]，拓展了外挂物分离等状态的研究途径，国外在这方面已经取得很大成就[7-8]。

本文综合运用笛卡尔网格和结构重叠网格，提出一种新型重叠网格。运用基于CFD的非定常数值模拟方法，将飞行力学方程、空气动力学方程耦合求解，以标准投弹算例为验证算例。

1 网格技术

1.1 新型重叠网格

现阶段的重叠网格多以部件作为基本单元，例如在标准投弹算例中，对导弹做一套体网格，对机翼做一套体网格，两套体网格之间存在相互运动。这种形式的体网格有两个不足之处：(1)若部件外形较为复杂，则体网格的生成较为困难。(2)若部件之间相对运动时间较长，距离较远，部件之间可能会出现网格不匹配，导致计算无法继续。

为解决上述问题，提出一种新型重叠网格。这种重叠网格在生成线和面时就进行重叠，把复杂几何外形结构的整体拆分成简单几何外形结构的个体，分别生成面网格，每片面网格单独外推生成附面层网格(物面附近的体网格)。相邻面网格、体网格之间存在的重叠部分用作信息交换。用此方法对几何外形进行剖分，可以简单生成任意复杂外形结构的网格拓扑。

如图1所示，(a)为面网格，由弹翼翼梢面网格(有一部分“长”到弹翼翼面上形成重叠)、弹翼翼面面网格(有一部分“长”到弹体面网格上形成重叠)、弹体面网格三部分组成。(b)(c)(d)为三部分分别外推形成的体网格，(e)为(b)(c)(d)的组合体，(f)为全弹的体网格。

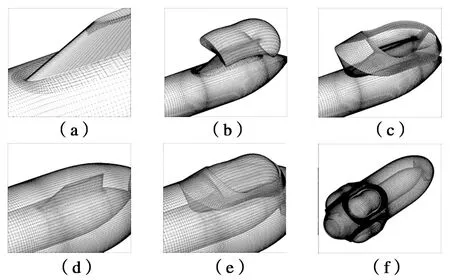
图1 新型重叠网格

1.2 网格动态自适应

仅有物面附近的网格不足以满足气动力计算的要求，需有远场网格。选用笛卡尔网格作为背景网格具有生成简单、便于挖洞操作、易于做网格自适应等优点。

在CFD中，流动控制方程在离散过程中产生误差是不可避免的。提高离散格式的精度和加密网格将有助于减小误差。然而提高格式的精度和全区域的加密网格往往会带来存储量和计算量的较大增加，而自适应技术可有效地解决这一问题[9]。尤其在遇到多体相对运动的问题时，随着物体相对位置的改变，网格加密部分也需要进行相应的改变，以保证计算的效率和准确性。

网格的动态自适应是根据流场的计算结果和计算对象的位置信息，实时实地或人为指定每n真实时间步对网格进行加密或稀疏。本文的背景网格为笛卡尔网格，借鉴笛卡尔网格的剖分思想引入父子关系。网格自适应分为自适应加密算法和自适应稀疏算法。

自适应加密算法步骤如下：

(1) 根据梯度大小(压力、马赫数、温度等)对流场区域进行划分，若梯度值符合要求，便将该类网格标记为A，对标记为A的网格，若相邻有多于两个A网格则对此网格标记为“加密”。

(2) 将标记为“加密”网格的所有面标记为“加密”，处理被加密的面，将标记为“加密”面的所有边标记为“加密”，在边的中点插入新节点，形成边上的悬点，生成两条边，记录边的父子关系。

(3) 对每个面进行循环，如果该面标记为“加密”，则：

a.在面心处插入新节点，形成面上悬点；

b.将新节点与每条边上悬点连接，形成新边；

c.将新边与原有的边连接形成新面，并记录父子关系。

(4) 对每个网格进行循环，如果该网格标记为“加密”，则：

a.在格心处插入新节点；

b.将新节点与每个面上悬点连接，形成新边；

c.将新边与原有边连接形成新面；

d.将新面与原有的面连接形成新网格，并记录父子关系。

(5) 处理未标记为“加密”但有悬点的边的面，生成新的子面，处理未标记为“加密”但有悬点的面的网格，生成新的子网格。

自适应稀疏算法与自适应加密算法是相交的过程，不再详述。经过自适应加密以及稀疏之后的笛卡尔网格能很好地适应计算条件，优化计算速度以及计算准确性。

1.3 三线性插值

重叠网格须通过插值的方式实现网格之间的数据交换。交换数据的重要形式是质量、能量和动量通量。如果流动中存在激波或大梯度物理区跨越插值洞边界时，须使用守恒型插值方法来正确捕捉激波。对基于密度求解法的可压缩流动来说，国外研究者[4]认为三线性插值方法具有保证正常精度的能力，这一结论已经得到许多数值实验的证实。

本文使用三线性插值来进行重叠网格之间的数据交换。引入型函数思想来解决重叠区域三线性插值问题。精度为二阶精度，能适应任何形状的插值问题。该方法计算简单，对重叠网格的计算结果较好。三维问题的控制体为类似于六面体的单元，如图2所示。

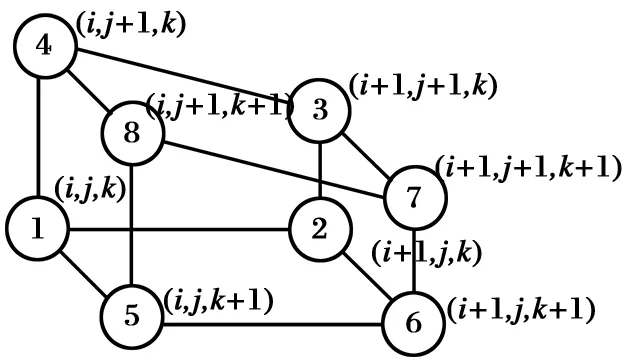
图2 六面体控制单元

假设顶点为Ai(i=1, 2, …, 8)，按逆时针进行排序。对其进行局部坐标变换，变换到(ξ,η,ζ)上的单元立方体。变换后顶点Ai(i=1, 2, …, 8)在(ξ,η,ζ)中的坐标为A1(0, 0, 0)；A2(1, 0, 0)；A3(1, 1, 0)；A4(0, 1, 0)；A5(0, 0, 1)；A6(1, 0, 1)；A7(1, 1, 1)；A8(0, 1, 1)。因为顶点Ai(i=1, 2, …, 8)的局部坐标系(ξ,η,ζ)取值为0或1，型函数可以写为

φi=(-1)1+ξi+ηi+ζi(ξ+ξi-1)(η+ηi-1)(ζ+ζi-1) (i=1, 2, …, 8)

(1)

上式为三线性，即对于ξ,η,ζ都是线性的。

然后进行坐标变换，目的是由网格点(x,y,z)求当前面网格局部坐标(ξ,η,ζ), 其中：

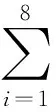
(2)

同理，y,z可求得。

这三组数据组成三个方程、三个未知变量的非线性方程组，采用牛顿迭代法求解该非线性方程组, 即可得到(ξ,η,ζ)。

2 数值模拟方法

2.1 流动控制方程及求解器

运用三维非定常可压缩Navier-Stokes方程为流动控制方程。一般曲线坐标系中，无量纲化的方程守恒形式为[10]

(3)

式中:Q为守恒矢量；F,G,H为对流通量；Fv,Gv,Hv为粘性通量；ξ,η,ζ为三个贴体坐标系方向；t为时间；Re∞为自由来流雷诺数。

流场求解采用基于结构网格的Roe Upwind格式和van Albada限制器。湍流模型选择Spalart-Allmaras一方程模型，该模型是从量纲分析和经验出发，针对简单流动逐步发展起来的模型，其容错功能好，处理复杂流动能力强，同时相对于两方程模型计算量小、稳定性好，有较高精度。

时间推进采用双时间步法，为了加速收敛，使用网格分块算法和网格分块并行计算技术。

2.2 六自由度刚体运动方程

本文算例的变形相对飞行器的尺寸较小，其运动可以近似采用刚体来描述。而刚体的运动可以分为两部分：质心的运动和物体绕质心的转动。

刚体动力学方程如下[11]：

(4)

刚体运动学方程如下[11]：

(5)

式中：m为刚体质量；V为速度；P为推力；X，Y，Z分别为阻力、升力、侧向力；α,β分别为攻角、侧滑角； ϑ为弹道倾角；Ψv为弹道偏角；θ,Ψ,φ分别为俯仰角、偏航角、滚转角；rv为速度滚转角；J为转动惯量；ω为角速度；M为力矩。

3 验证算例

为了验证本文方法，以实验数据较为全面的标准弹翼分离作为验证算例。该算例来源于美国空军实验室进行的外挂物分离实验研究，风洞实验在阿诺德工程发展中心(AEDC)4英尺跨音速空气动力风洞进行，具有比较完备的实验数据[3]。机翼翼型为NACA 64A010。

模型的尺寸如图3所示，计算条件如表1所示。为了直观显示结果数据，弹体坐标系定义为：坐标原点为导弹质心，X轴沿导弹纵轴指向前方，Z轴为0时刻重力方向，Y轴符合右手定则，0时刻地轴系与弹体坐标系重合。

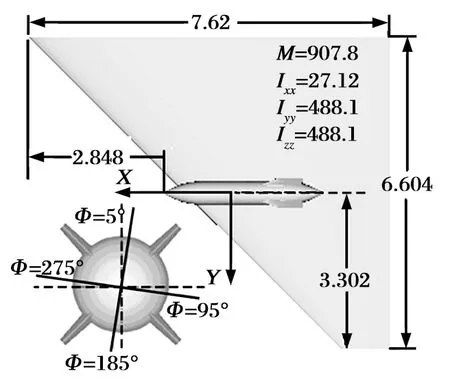
图3 模型比例示意图

表1 计算条件

外挂物质心位置和线速度变化曲线见图4～5。总的来说，在所显示的时间范围内，计算得到的质心线速度和位移与实验值都比较吻合。

外挂物的姿态和角速度的时间历程见图6～7，p，q，r分别为弹体系XYZ轴的三个角速度分量，φ，θ和Ψ分别为滚转角、俯仰角和偏航角，用来表示从地轴系到弹体系的变换。对于俯仰运动来说，在分离初始阶段，弹射力产生较大的抬头力矩，弹射力维持的时间到t=0.055 s，之后弹射力作用消失，作用在外挂物上的气动力和力矩开始起主导作用，这时候气动力产生的是低头力矩，在t=0.2 s以后，外挂物开始下俯运动，在偏航方向和滚转方向，计算的偏航角和滚转角与实验值吻合良好。

图8～9分别给出了气动力和气动力矩的时间历程比较。从气动力方面来看，除了初始的Cy计算值略小于实验值之外，其他方面都吻合良好； 对气动力矩来说，滚转力矩和偏航力矩吻合较好，初始俯仰力矩Cmy略小于实验值。俯仰力矩的偏差直接导致俯仰角θ出现误差。

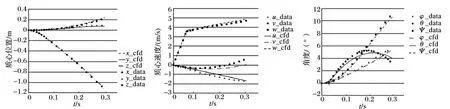
图4 质心位置曲线 图5 质心速度曲线 图6 俯仰、偏航、滚转角曲线

图7 角速度曲线 图8 力系数曲线 图9 力矩系数曲线

4 结 论

本文采用新型混合重叠网格生成方法，运用耦合六自由度方程的非定常数值模拟，以标准投弹算例进行验证。可得出如下结论：

(1) 在复杂绕流的CFD计算中，新型混合重叠网格能够降低网格生成难度，保证主体每一部分网格质量；

(2) 网格动态自适应可保证每个计算步内主体附近的网格密度，适用于运动状态的计算；

(3) 外挂物投放过程数值模拟结果表明，本文提出的新型混合重叠网格算法为外挂物投放分离安全分析预测和优化设计提供了一种高效的解决方案，具有较高的工程应用价值。

[1] 达兴亚, 陶洋, 赵忠良. 基于预估校正和嵌套网格的虚拟飞行数值模拟[J]. 航空学报, 2012, 33(6): 977-983.

[2] 陶洋, 范召林, 吴继飞. 基于CFD的方形截面导弹纵向虚拟飞行模拟[J]. 力学学报, 2010, 42(2): 169-176

[3] Noack R W, Slotnick J P. A Summary of the 2004 Overset Symposium on Composite Grids and Solution Technology[C]∥43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 2005.

[4] Meakin R L. On the Spatial and Temporal Accuracy of Overset Grid Methods for Moving Body Problems[C]∥12th Applied Aerodynamics Conference, Fluid Dynamics and Co-Located Conferences, Colorado Springs, Colorado, 1994.

[5] Lee S, Park M, Cho K W, et al. A New Automated Chimera Method for Prediction of Store Trajectory[C]∥17th Applied Aerodynamics Conference, Fluid Dynamics and Co-Located Conferences, Norfolk, Virgina, 1999.

[6] 杨爱明, 乔志德. 基于运动潜逃网格的前飞旋翼绕流N-S方程数值计算[J]. 航空学报, 2001, 22(5): 434-436.

[7] Dougherty F C, Kuan J H. Transonic Store Separation Using a Three-Dimensional Chimera Grid Scheme[C]∥27th Aerospace Sciences Meeting, Reno, Nevada, 1989.

[8] Snyder D O, Koutsavdis E K, Anttonen J S R. Transonic Store Separation Using Unstructured CFD with Dynamic Meshing[C]∥33rd AIAA Fluid Dynamics Conference and Exhibit, Fluid Dynamics and Co-Located Conferences, Orlando, Florida, 2003.

[9] 蒋跃文. 基于广义网格的CFD方法及其应用[D]. 西安: 西北工业大学，2012.

[10] 闫超. 计算流体力学方法及应用[M]. 北京：北京航空航天大学出版社，2006: 18-25.

[11] 李新国，方群.有翼导弹飞行动力学[M]. 西安：西北工业大学出版社，2008: 48-49.

A Numerical Simulation Method Based on the New Dynamic Mixing Overlapping Grid

Liu Chao, Liu Xianming, Wang Liqiang

(China Airborne Missile Academy，Luoyang 471009，China)

During launching of the external-carried missile, the missile is in a complex flow field of airborne, which will cause the unsteady and nonlinear characteristics of aerodynamic. At this time, using common method of wind tunnel test data interpolation as the aerodynamic data base will create error to a certain extent. An unsteady numerical simulation method based on the computational fluid dynamics (CFD) is proposed, and the flight mechanics equations and aerodynamic equations are coupled and solved, so as to simulate the real flight status more accurately. Compared with the past overlapping grids, the used new dynamic mixing overlapping grid has advantages such as easy generation, selfadapting adjustment for moving process. Taking the standard bomb-dropping example as a verification example, the results indicate the engineering importance of the dynamic mixing overlapping grid and the numerical simulation method.

dynamic mixing overlapping grid； unsteady； dynamic self-adapting； tri-linear interpolation； six-degree of freedom

10.19297/j.cnki.41-1228/tj.2016.06.010

2016-01-05

刘超(1991-)，男，黑龙江牡丹江人，硕士，研究方向为飞行器设计。

TJ760.11

A

1673-5048(2016)06-0044-05