锯齿形石墨烯纳米带特性的理论研究
陈 芡, 胡冬生, 徐 江
(南京航空航天大学 a.理学院; b.材料学院, 南京 211106)
锯齿形石墨烯纳米带特性的理论研究
陈 芡a, 胡冬生a, 徐 江b
(南京航空航天大学 a.理学院; b.材料学院, 南京 211106)
对具有一定宽度的锯齿形石墨烯纳米带用对角化其哈密顿的方法自洽地计算了电子在半填满的情况下石墨烯的性质,结果发现:锯齿形石墨烯带在相同条件下两边之间是铁磁耦合还是反铁磁耦合是随机的.两边之间呈现反铁磁序时,石墨烯带是半导体,其带隙具有量子限制效应;呈现铁磁序时,石墨烯带是导体.无论哪一种情况,石墨烯带边缘原子的磁序都是一个定值,并不随系统大小而变化,这就为石墨烯作为自旋电子学的材料提供了一个无比优越的条件.
石墨烯;磁序;自洽计算
因石墨烯在微电子和光电子器件领域有着非常广阔的应用前景,近年来石墨烯奇特的物理性质和化学性质吸引了科学研究者的关注.其结构是由碳原子组成的蜂窝状的二维系统,碳碳之间通过sp2轨道杂化.2004年,石墨烯在实验室首次被分离出来[1].在此之前,已有研究表明石墨烯纳米带晶体边缘的取向对电子结构有重要的影响[2].按晶格的取向,经裁剪得到的石墨烯纳米带有两种边界:锯齿形和扶手形.不同边界的石墨烯所具有的电和磁的特性差异很大.扶手形边界的石墨烯纳米带的能带具有量子限制效应,是半导体材料,其本身不具有磁性,但是如果碳纳米管或者石墨烯表面吸附了某些原子团,如钛原子链,就会产生磁性[3].锯齿形边界的石墨烯纳米带表现出金属性,其边缘态变化较平缓,边缘具有磁序[3-5].理想的石墨烯本身并没有磁性,其磁性主要来自于缺陷、杂质、边界[6].密度泛函理论研究表明:锯齿形的石墨烯纳米带出现磁性是由费米能附近局域电子态的自旋极化产生的[7].这样的自旋极化在同一边界呈现铁磁耦合,两边界之间呈现反铁磁耦合[8].锯齿形石墨烯纳米带的边缘态效应所产生的磁性和与之有关的帯隙一直受到关注,人们用各种方法来研究这一问题,如第一性原理密度泛函理论[4],基于哈伯德模型的平均场方法[9],量子蒙特卡罗方法等等[10].这些研究表明:锯齿形的石墨烯纳米带边界的磁性是较稳定的.实验也证明在低温下(7K)石墨烯纳米带存在磁性[11].2014年,Magda G Z等人在纳米尺度上制造出晶体边缘取向很好的锯齿形石墨烯纳米带和扶手形石墨烯纳米带[12].通过测量发现:锯齿形石墨烯纳米带在小于7纳米的时候会有0.2~0.3电子伏特的能带间隙,具有半导体的特性,纳米带两边呈现反铁磁序;当纳米带宽度大于8纳米时表现为金属的特性,两边呈现铁磁序.这就意味着锯齿形纳米带随着宽度的增加,会有从半导体到金属的转变.然而要得到完整边界的石墨烯并不容易,但用氟单原子链耦合到边缘就可以得到完整边界的锯齿形石墨烯[13].
1 模型与方法
锯齿形石墨烯纳米带的结构如图1所示.在X方向上具有平移对称性,Y方向是有边界的.

图1 锯齿形边界石墨烯纳米带的示意图
该系统可用哈伯德模型来描述,其哈密顿为:
(1)

(2)
因此石墨烯带的哈密顿可写为:
(3)
石墨烯纳米带在X方向是周期性结构,可以把X方向的算符由实空间转化到动量空间(k空间),而在Y方向上的保持为原来的实空间.由于石墨烯由两套子格构成,分别用A,B表示,有S条链的石墨烯带在Y方向的实空间中就有2S个格点.考虑电子的自旋,石墨烯带的哈密顿可以写成4S×4S的矩阵:
(4)
其中,Hσ(σ=↑,↓)是2S×2S的矩阵,
(5)
HAσ′,HBσ′,HF′和HF′*都是S×S的方阵;HF′*是HF′的厄米矩阵.
(6)
(7)
(8)

2 结果和讨论
在计算中t0取值为1,U取值为2,粒子数为半满,温度T为300K.调节化学势μ,经过自洽计算,求出不同宽度石墨烯纳米带各格点的磁序.通过对锯齿形石墨烯带的条数S=10,20,30,35,40,50,60,70,80,90,100的自洽计算,且每种宽度都独立计算了100次,发现即使石墨烯纳米带宽度相同,计算的参量也相同,石墨烯纳米带两边之间不是出现铁磁序就是出现反铁磁序,并且是随机的.图2是相同参数条件下宽度为30条和100条时的两种情形,其中i是原子从纳米带一边到另一边的编号,(a)、(b)图为宽度30条时各格点的磁序M随格点位置i变化的两种情况,(a)图呈现反铁磁序,(b)图呈现铁磁序.(c)、(d)图是宽度为100条时的情形.

图2 锯齿形石墨烯带的各原子磁序随位置的变化
当锯齿形石墨烯带两边之间分别为反铁磁和铁磁时,其能带结构如图3,(a)、(b)图分别为10条时反铁磁和铁磁的能带图,(c)、(d)图分别为30条时反铁磁和铁磁能带图.从图中可以看到当锯齿形石墨烯带的两边之间是反铁磁序时,能带图呈现半导体的性质,而当两边之间是铁磁序时呈现的是导体的性质,此时能带图中导带和价带之间出现了交叉,是石墨烯带两边之间呈现铁磁序时的边缘态.当不考虑电子与电子相互作用,呈现铁磁序时,其边缘态是简并的平态[2],因考虑了电子-电子相互作用,其简并的平态分裂形成交叉,交叉的两个态分别对应于石墨烯带一边缘的自旋向上态和另一边缘的自旋向下态.

图3 锯齿形石墨烯带的能带结构图
石墨烯带两边呈现反铁磁序时是半导体,其带隙与宽度之间的关系如图4所示.从图中可以看出带隙随宽度增加而减小.通过对计算的理论值进行曲线拟合,我们发现带隙随宽度的变化关系为ΔE=3.8272·S-1.034,说明石墨烯条两边是反铁磁序时存在量子限制效应.
我们通过计算发现无论什么宽度的石墨烯带边缘原子的磁序都是一个定值,并不随宽度变化,如图5所示.这个性质为石墨烯作为磁性材料提供了无比优越的条件.
我们对不同宽度的石墨烯纳米带的磁序各计算了100次.图6是对100次计算结果进行的统计,表示了两边之间出现铁磁耦合和反铁磁耦合的概率与宽度之间的关系.
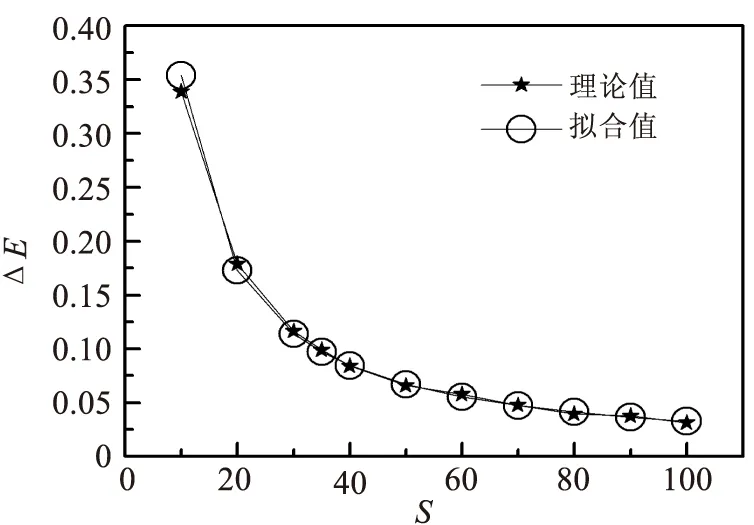
图4 反铁磁序时带隙随宽度S变化的曲线图

图5 边缘磁序随宽度的变化关系图
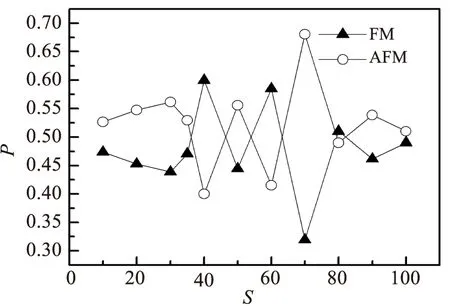
图6 概率P随着带宽S的变化
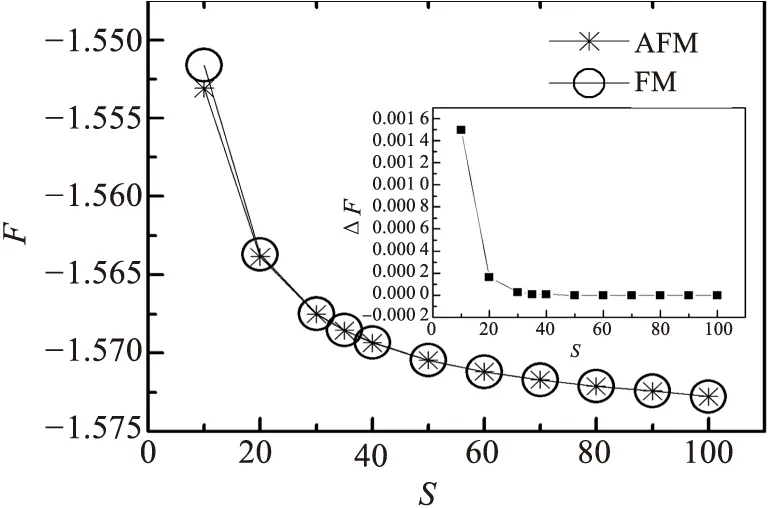
图7 自由能F随着带宽S的变化曲线
从图6可以看出,当锯齿形石墨烯带的条数小于35条时,出现反铁磁磁序的概率比出现铁磁序的概率大;当锯齿形石墨烯带的条数大于35条时,反铁磁磁序和铁磁磁序出现的概率没有规律.实验中观察到锯齿形石墨烯的宽度在小于7纳米时,两边界呈反铁磁耦合,大于7纳米时呈铁磁耦合[12].宽度为35的石墨烯纳米带实际宽度大约为7.313纳米,我们的计算结果显示常温下石墨烯纳米带不是呈现反铁磁就是呈现铁磁,且在小于此值时,出现反铁磁的概率总比出现铁磁的概率大.
为了进一步说明锯齿形石墨烯纳米带一定带宽时,其两边出现铁磁序还是反铁磁序,我们计算了不同宽度石墨烯纳米带的自由能F.从图7中可以看出反铁磁的自由能总是比铁磁的小,它们的差值随宽度的增加迅速减小.当宽度增加到35之后,可以看成两者几乎相等了.石墨烯处于铁磁状态还是处于反铁磁状态并不能由自由能确定,因为铁磁态和反铁磁态是两个孤立的状态,并不能说自由能低就一定处于该状态,自由能高的态也应该是一个亚稳态,所以只能说自由能低的态出现的概率应该大些.当然我们的计算是基于每个位置的电子是半填满,且是完美的石墨烯带,而实验得到的石墨烯带有可能不是完美的,电子占有数也不一定半填满,可能还有其他很多因素.
3 结论
我们用平均场的方法自洽的计算了电子占有数在半满的情况下,存在电子-电子相互作用的锯齿形石墨烯纳米带的特性.结果表明:锯齿形石墨烯带在相同条件下两边之间是铁磁耦合还是反铁磁耦合是随机的.两边之间呈现反铁磁序时,石墨烯带是半导体,其带隙具有量子限制效应;呈现铁磁序时,石墨烯带是导体.无论哪一种情况,石墨烯带边缘原子的磁序都是一个定值,并不随石墨烯宽度而变化,这一特性为石墨烯作为自旋电子学的材料提供了一个无比优越的条件.
[1] NOVOSELOV K S,GEIM A K,MOROZOV S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306(5696):666-669.
[2] FUJITA M,WAKABAYASHI K,NAKADA K,et al.Peculiar localized state at zigzag graphite edge[J].Journal of the Physical Society of Japan,1996,65(7):1920-1923.
[3] KAN E J,XIANG H J,YANG J,et al.Electronic structure of atomic Ti chains on semiconductinggraphene nanoribbons:a first-principles study[J].The Journal of Chemical Physics,2007,127(16):164706.
[4] SON Y W,COHEN M L,LOUIE S G.Energy gaps ingraphene nanoribbons[J].Physical Review Letters,2006,97(21):216803.
[5] NAKADA K,FUJITA M,DRESSELHAUS G,et al.Edge state in graphene ribbons:Nanometer size effect and edge shape dependence[J].Physical Review B,1996,54(24):17954-17961.
[6] KAN E,LI Z,YANG J.Magnetism ingraphene systems[J].Nano,2008,3(6):433-442.
[7] ENOKI T,TAKAI K.The edge state of nanographene and the magnetism of the edge-state spins[J].Solid State Communications,2009,149(27):1144-1150.
[8] SON Y W,COHEN M L,LOUIE S G.Half-metallicgraphene nanoribbons[J].Nature,2006,444(7117):347-349.
[9] JUNG J,MACDONALD A H.Carrier density and magnetism ingraphene zigzag nanoribbons[J].Physical Review B,2009,79(23):235433.
[10]GOLOR M,LANG T C,WESSEL S.Quantum Monte Carlo studies of edge magnetism in chiral graphene nanoribbons[J].Physical Review B,2013,87(15):155441.
[11]TAO C,JIAO L,YAZYEV O V,et al.Spatially resolving edge states of chiral graphene nanoribbons[J].Nature Physics,2011,7(8):616-620.
[12]MAGDA G Z,JIN X,HAGYMSI I,et al.Room-temperature magnetic order on zigzag edges of narrow graphene nanoribbons[J].Nature,2014,514(7524):608-611.
[13]MAKAROVA T L,SHELANKOV A L,ZYRIANOVA A A,et al.Edge state magnetism in zigzag-interfaced graphene via spin susceptibility measurements[J].Scientific Reports,2015,5:13382.
[责任编辑 王新奇]
The Theoretical Research on Characteristics ofZigzag Graphene Nanoribbons
CHEN Qiana, HU Dong-shenga, XU Jiangb
(a.School of Science; b.School of Materials, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)
The properties of zigzag edges of graphene nanoribbons with different widths are self-consistently calculated by the method of diagonalizing the hamiltonian. The results show that appearance of ferromagnetism or antiferromagnetism in two edges of the nanoribbon is random at the same condition. The ribbons is semiconductor and the band gap has a quantum confinement effect with the appearance of antiferromagnetic order between the two sides. The ribbons is conductor with the appearance of ferromagnetic order. In either case, the magnetic order of atoms along edges is a constant value, and it does not change with the size of system. All of these provide an incomparably superior condition for taking graphene as the material of spintronics.
graphene; magnetic order; self-consistent calculation
1008-5564(2016)05-0001-06
2016-02-22
国家自然科学基金(51374130)资助课题
陈 芡(1990—),女,山东德州人,南京航空航天大学理学院物理系硕士研究生,主要从事超导和磁性研究.
TB383
A

