基于小波正则化重构镐型截齿载荷谱的时频特性

付守奎， 任春平

(1.黑龙江煤矿安全监察局, 哈尔滨 150001； 2.哈尔滨工程大学 机电工程学院， 哈尔滨 150001；3.黑龙江科技大学 机械工程学院， 哈尔滨 150022)

基于小波正则化重构镐型截齿载荷谱的时频特性

付守奎1， 任春平2，3

(1.黑龙江煤矿安全监察局, 哈尔滨 150001； 2.哈尔滨工程大学 机电工程学院， 哈尔滨 150001；3.黑龙江科技大学 机械工程学院， 哈尔滨 150022)

为探寻镐型截齿旋转破碎煤岩载荷时频谱特性规律，研究其载荷谱能量分布特征与截割过程的映射关系，以期实现截割破碎煤岩载荷谱的定量重构。利用小波正则化方法建立截齿旋转破碎煤岩载荷谱重构模型，确定不同频段其载荷谱能量特征分布。结果表明：实验载荷谱能量随旋转破碎循环次数的增加呈先增大后减小变化，其能量特征可表征截齿破碎过程，重构载荷谱能量主要分布在低频段，在高频段其能量幅值较小，重构与实验载荷谱能量差值变化率在15%以内。该研究可以为实现高效旋转破碎煤岩判定方法提供参考。

镐型截齿； 载荷谱； 小波正则化； 重构； 能量分布

在截齿截割破碎煤岩过程中，切削厚度是变化的，且该过程连续进行。因此，测试实验的破碎煤岩载荷谱是一种非平稳和含有噪声的信号，严重影响载荷谱的质量及其对真实载荷谱的认知程度。若从载荷谱的时域波形判断截齿截割状态往往会产生一定的误差，从混有噪声的截割载荷谱中识别及提取有用的信息，降低噪声对载荷谱的影响一直是研究的关键。近年来，降低噪声的方法主要为人工神经网络、裂谱(倒谱)分析法、解卷积法、自适应滤波方法等，但都局限在时域(频域)上分析问题。小波正则化方法具有良好的时域和频域局部化特性，可作为分析非平稳信号的有效工具。据此，以小波正则化为研究方法，对截割实验载荷谱进行重构研究，分析其时频谱特性及能量特征分布规律，确定截割载荷谱能量分布特征与破碎煤岩过程的映射关系，从而实现截割载荷谱的定量重构。

1 小波分析变换

设ψ(t)L2()，L2()为实数空间，ψ(ω)为其FFT变换形式。当ψ(ω)具备下列条件时[1-2]

Cω∫，

(1)

称ψ(ω)为一个母小波，若将ψ(ω)平移或伸缩，从而获得一个小波序列，当小波序列为连续状态时，可表示为：

(2)

式中：a——伸缩因子；

b——平移因子。

当其为离散状态，小波序列为：

ψj,k(t)=2-j/2ψ(2-jt-k)，

(3)

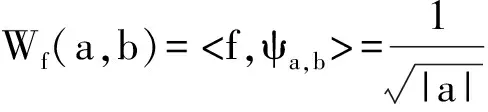
(4)

小波变换在时域(频域)取样步长对其不同频率成分具有调节的作用，即当高频取样小步长，其对应于j值小；低频取样大步长，其对应于j值大。

CAS小波定义在区间[0,1]上，表达式为[3-4]：

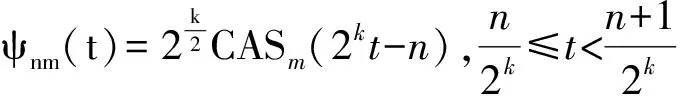
(5)

式中:CASm=cos(2mπt)+sin(2mπt)。

由于CAS小波形成了实数空间L2()的一组标准正交基，其展开形式为：

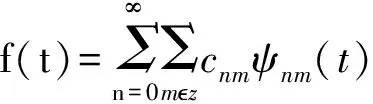
(6)

当式(6)为截断，其表达式为：

(7)

式中：C——2k(2m+1)×1维的系数向量，C=[C0(-M)，C0(-M+1)，…，C(2k-1)M]T；

ψ(t)——2k(2m+1)×1维的基向量函数，ψ=[ψ0(-M),ψ0(-M+1),…,ψ(2k-1)M]T。

2 截齿破碎煤岩实验

2.1 破碎煤岩实验

截齿旋转破碎煤岩实验台[7]，滚筒转速为41 r/min，牵引速度0.612 m/min，楔入角为35°，截割阻抗180～200 kN/m，切削厚度15 mm，截齿类型为六棱形，其长为160 mm，齿身长度为90 mm，齿柄直径为φ30 mm，齿尖合金头长度为14 mm，截割对象为人工制造的煤壁，测试得到截齿沿轴向方向的截割载荷曲线，如图1所示。

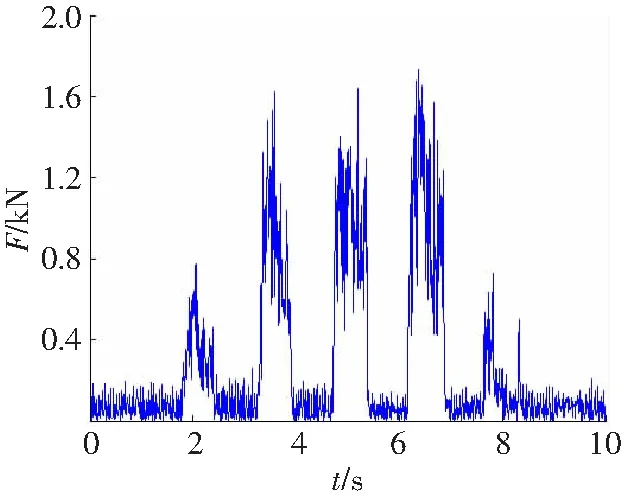
图1 截齿破碎煤岩实验载荷谱

2.2 实验结果分析

从图1实验载荷谱时域波形可知，截齿破碎煤岩载荷谱为一种非平稳信号，其载荷的局部增大或者减小交替进行，表现出不规则的变化规律，为了快速地识别载荷谱的截割规律和波形特征，给出实验载荷谱的拟合宏观轮廓曲线及其峰值轮廓拟合曲线，如图2所示。由图2可知，该拟合轮廓能够直接反映出截割载荷谱的特征量变化，体现了截割状态总体变化趋势。其载荷谱的每个截割循环曲线轮廓拟合图呈月牙形，表征截齿破碎煤岩得到的载荷谱，呈现出随切削厚度增大而变大的趋势，当处于最大切削厚度，此时的载荷谱也同时达到最大，随后又慢慢地减小，这与采煤机的实际工况相吻合。

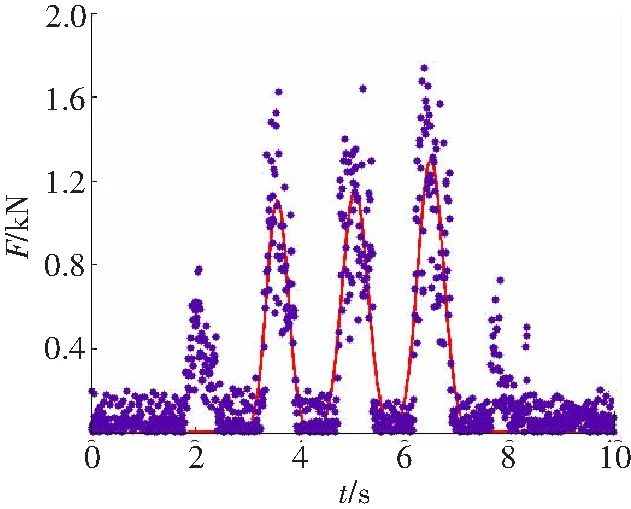
a 载荷轮廓拟合

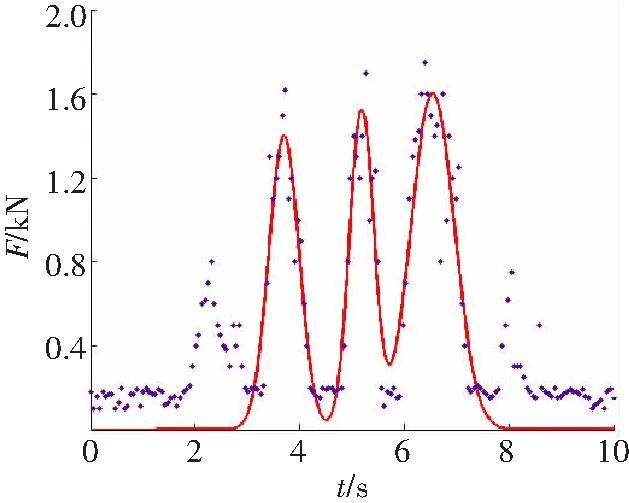
b 载荷峰值轮廓拟合

截齿破碎煤岩载荷谱分为稳态截割载荷分量和动态截割载荷分量，稳态截割载荷分量可用截割载荷的均值量描述，动态截割载荷分量可以用能量特征来表征。实验载荷拟合轮廓曲线表征的是载荷谱的均值量，为稳态的截割载荷分量。为了探讨动态截割载荷分量变化对截割过程的影响，在时域范围内，提取动态载荷谱的能量分布η特征，给出其能量分布随截齿截割循环次数n的变化规律，见图3。

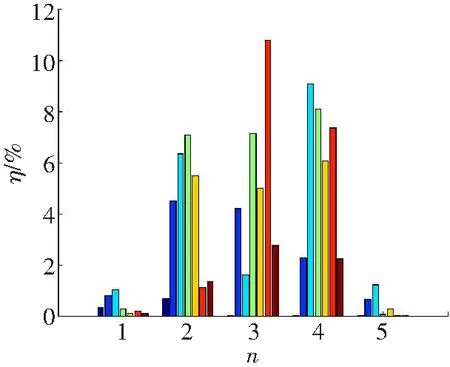
图3 动态载荷的能量分布

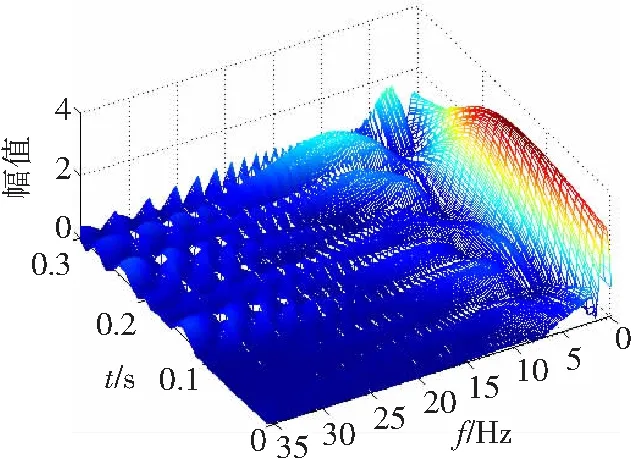
从图3可知，截割载荷动态分量的能量百分比随截齿截割循环次数的增加呈先增大后减小的变化，每个截割循环下其能量分布形状也与截割面类似呈月牙形状，其原因在于随着切削厚度的增大，截齿破碎煤岩所需能量逐渐变大，当煤岩慢慢地逐渐崩落的过程中，能量逐渐释放，能量百分比逐渐减小。因此，载荷动态分量的能量百分比特征能够间接反映截齿破碎煤岩的过程，可作为判断破碎煤岩过程与其能量分布关系的特征参数。为更加深入具体地探索实验截割载荷谱特性，若仅从时域范围研究载荷谱特性还不够完善。据此，根据小波变换给出了截割载荷的三维时频谱，如图4所示。

图4 截割载荷三维时频谱

从图4可知，当频率在1～5 Hz范围，截割载荷幅值逐渐减小。当频率大于5 Hz时，其幅值下降到一定程度，其在一定幅值范围内上下波动。载荷幅值随时间的增长呈先增大后减小的变化。因此，该三维时频谱表明截割能量集中在低频区域，同时出现特征频率(幅值最大所对应的频率)，其可作为载荷谱频域特性的参考量。

3 重构截割载荷时频谱特性

3.1 小波-正则化

设z(t)为重构的截割阻力载荷谱，f(t)为实验截割阻力载荷谱，根据Cadzow提出的重构算法，建立Fredholm方程[5]：

∫bah(t-τ)z(τ)dτ=f(t)，t(a,b)，

(8)

由于实验测试得到的载荷谱f(t)含有一定的噪声，即fδ(t)=f(t)+δe(t)，t(a,b)，这里假设δ=1为高斯白噪声，fδ(t)=f(t)+e(t)，所以式(8)等价于式(9)：

∫bah(t-τ)z(τ)dτ=fδ(t)，

(9)

式中：fδ(t)L2即fδ(t)属于Hilbert空间。

(10)

整理得

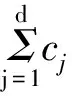
(11)

化简：

CA=F，

(12)

式中：C={c1,c2,c3,…,cj}；

A=∫bah(t-τ)ψj(t)dt；

F={f1,f2,f3,…，fj}。

令r(t)为参差函数,r(t)=CA-F,设=0，则有等式成立[6]：

C=，

(13)

与式(13)等价的方程为：

BC=D，

(14)

式中：B=∫ba∫bah(t-τ)ψjψidtdx；

C={c1,c2，…,cj};

D=∫bafδ(t)ψidt。

(BTB+λI)C=BTD，

(15)

只要求得方程(15)中的系数C，则

(16)

就是唯一确定，由于正则参数未知，因此，正则参数的选取至关重要。

3.2 正则参数的选取

广义交叉法(GCV)在求解正则参数时具有计算简单、效率高的特点，因此，根据载荷谱重构模型，基于Golub提出的基本思想，给出其应用公式，其最小值处取值即为正则参数，正则参数λ应满足下列等式[7-10]：

(17)

式中A(λ)=A(ATA+λ2I)-1AT；

tr(A)——矩阵A的迹

根据式(17)及实验载荷谱运动参数和结构参数，给出了GCV曲线，如图5所示。从图5可知，当正则参数0≤λ≤0.01时，GCV(λ)的数值逐渐下降，当正参数0.01<λ≤0.1时，GCV(λ)的值逐渐上升，即当正则参数λ=0.01时，GCV(λ)取得最小值。因此，采用广义交叉法得到的正则参数λ=0.01。

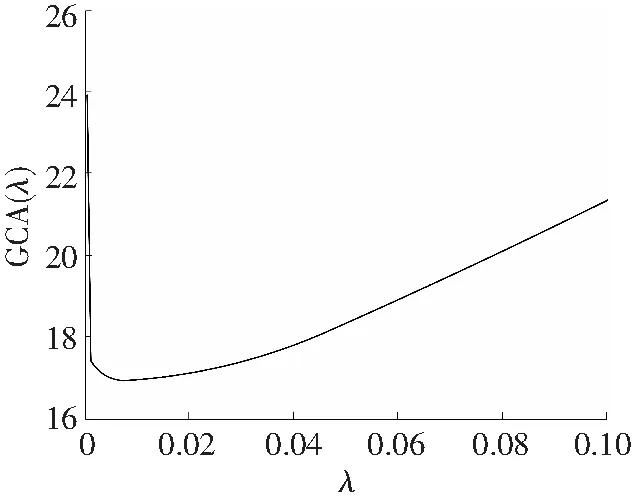
图5 GCV法

3.3 重构结果与分析

以截取实验载荷谱曲线峰值最大段的前0.3 s曲线为研究对象，ΔT=0.01，N=31，λ=0.01，基向量函数ψj(t)=2(cos8πt+sin8πt)[11-17]，根据上述小波正则化算法，给出其重构载荷谱的效果，见图6。

图6 重构效果

图6表明，截割载荷谱重构效果比较理想，其波形较光滑平稳，其总体趋势与实验有较好的吻合度。为研究重构载荷谱频谱特性的变化，根据小波变换给出了实验与重构载荷谱的三维时频图，见图7。从图7可知，重构截割载荷幅值在高频区域比较光滑平稳，信号极其稳定，表明重构后的载荷谱高频成分被滤掉，其能够清晰表征截割载荷在去噪后的真实截割状态。为了更加方便清楚得到时间与频率，频率与幅值关系，给出载荷谱的二维时频谱，见图8。从图8可以清晰看到，随着时间的增长，重构载荷频率与实验载荷频率主要集中连续分布在同一个区域，特征区别不够明显。随频率的增加，实验载荷幅值主要集中在低频段，高频区域载荷幅值减小，且不够稳定，重构载荷幅值也集中在低频段，但高频段幅值较小平稳，表明重构后的载荷噪声较小，其特征便于应用和提取。

a 实验

b 重构

a 实验

b 重构

为了进一步探索重构后的截割载荷能量分布规律，通过统计分析，给出了镐型截齿截割载荷谱能量百分比在不同频率段的变化柱状图，见图9。从图9可知，载荷谱最大能量百分比主要处在低频段，集中在1～3 Hz，随着频率的增大其能量百分比特征逐渐较小，但重构载荷能量百分比特征在高频段内变化不大，而实验载荷能量百分比特征在高频段呈交替增大减小的变化，且两者能量差值变化率在15%以内。原因是实验载荷谱附有噪声的干扰，而重构载荷谱在高频段已经把噪声滤去，所以造成两者能量差值的变化，符合实际要求。

图9 不同频段的载荷能量分布

4 结 论

(1)实验载荷谱能量随截割循环次数的增加呈先增大后减小变化，其能量特征可表征截割过程。

(2)以截齿破碎煤岩获得的实验载荷谱为研究基础，应用小波-正则化技术，实现其载荷谱的定量重构，给出不同频段区域载荷的能量分布特征，重构载荷谱能量主要分布在低频段区域，在高频段其能量幅值较小，重构与实验能量差值变化率在15%以内。因此，载荷谱的能量分布特征能够表征煤岩破碎状态及过程。

(3)该研究符合实际要求，可以为实现高效破碎判定提供参考。

[1] 刘春生, 李德根. 基于单截齿截割实验条件的截割阻力数学模型[J]. 煤炭学报, 2011, 36(9): 1565-1568.

[2] RAJAN M P. Convergence analysis of a regularized approximation for solving Fredholm integral equations of the first kind[J]. J Math Anal Appl, 2003, 27(9): 522-530.

[3] 王延新, 韩慧丽. 求解第一类Fredholm积分方程的小波-正则化方法及外推[J]. 科学技术与工程, 2010, 10(1): 17-19.[4] 王延新, 韩慧丽. 第一类Fredholm积分方程的CAS小波解法[J]. 四川兵工学报, 2009, 30(2): 127-129.

[5] ALI ASHTARI. Signal processing methods for high resolution microwave image reconstruction[D]. Canada: Department of electrical and computer engineering university of manitoba, 2009.

[6] 肖庭延, 王彦飞.一维带限信号正则外推的快速算法[J]. 信号处理, 2001, 17(1): 31-36.

[7] 刘春生, 任春平, 鲁士铂, 等. 截齿截割载荷谱重构的正则参数优化策略[J]. 黑龙江科技学院学报, 2013, 23(5): 444-448.

[8] BILGIN N, BALCI C.Correlative study of linear small and full-scale rock cutting tests to select mechanized excavation machines[J].International Journal of Rock Mechanics & Mining Sciences, 2007, 4(4): 468-476.

[9] 刘春生,于信伟, 任昌玉.滚筒式采煤机工作机构[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010.

[10] 刘春生, 王庆华, 任春平.镐型截齿载荷谱定量特征的旋转截割实验与仿真[J].黑龙江科技大学学报, 2014, 24(2), 195-199.

[11] 任春平. 基于正则化算法的镐型截齿破碎煤岩载荷谱重构研究[D]. 哈尔滨： 黑龙江科技大学， 2014.

[12] 刘春生，李德根． 不同截割状态下镐型截齿侧向力的实验与理论模型[J]. 煤炭学报， 2016， 41(9) : 2359-2366．

[13] 刘春生， 韩 飞. 镐型截齿侧向载荷谱特性实验研究[J].黑龙江科技大学学报， 2016, 26(2): 177-182.

[14] HANSEN P C. The discrete Picard condition for discrete ill-posed problems [J]. BIT： 1990, 30(11)： 658-672.

[15] MARK A， LUKAS. Asymptotic optimality of generalized cross-validation for choosing the regularization parameter[M]. Berlin ：Numerische Mathematik， 1993.

[16] CALVETTI D, GOLUB G H.Estimation of the L-curve via lanczos bidiagonalization[J]BIT: 1999, 39(4): 603- 619.

[17] KILMER M E.Choosing regularization parameters in iterative methods for ill-posed problems[J]. SIAM J. Matrixanal, 2001, 22(4): 1204-1221.

(编辑 晁晓筠 校对 李德根)

Time-frequency characteristics of reconstruction load spectrum of conical picks based on wavelet regularization

FuShoukui1，RenChunping2，3

(1.Heilongjiang Coal Mine Safety Supervise Bureau, Harbin 150001,China; 2.College of Mechnical & Electrical Engineering, Harbin Engineering University, Harbir 150001, China; 3. School of Mechanical Engineering, Heilongjiang University of Science & Technology, Harbin 150022,China)

This paper seeks to investigate the law underlying the time spectrum characteristics behind conical picks working with coal-rocks by rotating and crushing, determine the mapping relationship between the distribution characteristics of load spectrum energy and cutting process, realize the quantitative reconstruction of the load spectrum of the picks cutting coal rocks, and reconstruct the experimental load spectrum The study consists of producing the experimental load spectrum of the picks working with coal rocks by rotating and breaking operation, and analyzing the time spectrum characteristics; using the wavelet regularization method to establish the load spectrum reconstruction model. The results show that experimental load spectrum energy sees a change from an initial increase to a subsequent decrease, depending on the increase in the numbers of rotating crusing cycles, exhibiting energy characteristics able to characterize the crushing process； indicating a difference of less than 15% between the reconstruction and the experimental load spectrum energy. The study may sever as the reference for the realization of high efficiency rotary broken coal rock judgment method.

conical pick； load spectrum; wavelet regularization; reconstruction；energy distribution

2016-10-10

付守奎(1965-)，男，山东省平度人，高级工程师，研究方向：煤矿机械，E-mail：renchunpin@sina.com。

10.3969/j.issn.2095-7262.2016.06.015

TD421

2095-7262(2016)06-0659-06

:A