具有离轴相位奇点的线偏振高斯光束特性研究
许江华, 庄松林
(上海理工大学 光电信息与计算机工程学院,上海 200093)
具有离轴相位奇点的线偏振高斯光束特性研究
许江华, 庄松林
(上海理工大学 光电信息与计算机工程学院,上海 200093)
通常所研究的相位奇点光束均为相位奇点位于光束光轴上的涡旋光束,也即涡旋轴与光轴重合,但在实际生成相位奇点光束和具体应用中,往往很难保证光束的涡旋轴与光轴完全重合.基于应用实际,研究了离轴的相位奇点对光束光强的影响以及具有离轴相位奇点光束的聚焦特性和应用价值.离轴的相位奇点将以其中心所在位置为旋转对称中心对整个光场的光强分布产生相干叠加的影响,同时,离轴相位光束的研究也为非均匀光强分布的生成提供了更多的选择.
相位奇点; 涡旋光束; 奇点光束; 离轴奇点; 光强分布
Technology,Shanghai200093,China)
相位奇点光束,即通常所说的涡旋光束,具有很多特殊的性质:存在相位不确定的相位奇点,具有螺旋状波前结构和独特的动力学特性,能形成暗中空的环形光束等.这一类结构的特殊光束在生物医学、粒子操控[1-5]等领域获得了广泛的研究与应用.涡旋光场中的光子具有mħ的轨道角动量,其聚焦形成的光学势阱能够和粒子之间发生动量和角动量的交换,通过传递角动量能够实现粒子旋转和操控,可以用来束缚或分离粒子,更有可能在分子设备中作为光学驱动来提供动力系统.并且具有确定的轨道角动量的光子在量子信息传输、光量子计算和加密量子通信等方面也表现出了巨大的潜力.所以如何输出稳定、高质量的涡旋光场成为人们研究的一个重点内容.关于产生涡旋光束,近几十年来,人们已经提出并尝试了很多种方法:几何光学模式变换法[6]、计算全息法[7-9]、螺旋相位板法[10-11]和液晶空间光调制器法[12]等,并且特定结构的开腔激光器也可以直接输出具有涡旋相位的高阶拉盖尔-高斯光等涡旋光束[13-14].然而,在产生涡旋光束的过程中,很难保证光束的涡旋轴与光场中心保持完全重合,也就是说生成涡旋光束中的相位奇点会存在一定的离轴量,光场的相位奇点偏离光束中心时,光强的分布特性将呈现出一定的不对称性,从而产生一些特殊的变化.本文将专门讨论相位奇点偏离光场中心的涡旋光场的特性.
1 单涡旋离轴相位奇点光束的数学基础
所谓单涡旋离轴相位奇点光束,即有且只有一个相位奇点的涡旋光束,并且相位奇点不在光束中心,即涡旋轴与光束光轴不重合.对于y方向上的线偏振高斯光束,拓扑荷数值为m的光学涡旋内嵌于点(ρs,φs)处,入瞳平面上电场分布可表示为
式中:r0和φ0分别为入射光场入瞳平面处的径向和方位角向坐标;ω0为光斑尺寸;ρs为相位奇点离轴距离.当φs=π/4,m=1时,离轴涡旋光束的光场强度和相位分布如图1所示.
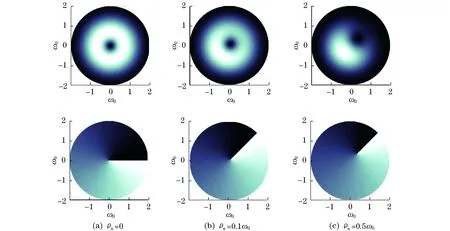
图1 离轴涡旋光束的光场强度分布和波前相位分布
可以看出,当涡旋相位奇点不在光轴上时,光束在涡旋核偏离方向上失去对称性,光场暗点位于相位奇点处,并且相位奇点偏离光轴一定距离之后,光场强度不再有明显空心暗斑,光场强度最大值归于一点,且沿着相位奇点偏离方向往光轴靠近.
对于涡旋拓扑荷数m=1的相位奇点光束,为了确定光场强度最大值的位置,考虑到相位奇点离轴方向上的对称性,以x轴方向上的离轴相位奇点光束为例,光强的最大值与最小值均位于x轴上,x方向上的电场分布可以表示为
(2)
式中,xs为相位奇点偏移量.对xs求导得
(3)
令上式等于零,解一元二次方程可以得到光场强度最大值位置为
(4)
显然,xsmax的符号与xs刚好相反,即光场强度最大值位置与相位奇点位置位于光束中心的相反方向上.图2为不同涡旋拓扑荷数下,光场强度最大值位置随着相位奇点偏离光轴时的距离变化,ρsmax和ρsmin分别为光场强度最大值和最小值的离轴量.显然ρsmin=ρs,光场强度最小值为零,且位于相位奇点处.当ρs=0时,相位奇点位于光轴上,随着拓扑荷数m的增加,光场暗斑尺寸也逐渐变大.而随着相位奇点偏离光轴越来越远,光场强度最大值的变化量越来越平缓,并且相位奇点在相同的离轴量下,光强最大值的离轴量与拓扑荷数近似成正比.

图2 不同涡旋拓扑数下光强极大值位置偏离量与相位奇点偏离量之间的关系
对于y方向上线偏振经物镜系统聚焦后,在焦点区域的电场分布可表示为
式中:θ为像方光束会聚角;k为波数;r2,φ为径向坐标;P(θ)为透镜的切趾函数;φ为相位差;λ为波长.
这里,入射光场振幅分布为高斯分布,在物镜入射光瞳面(ρs,φs)处引入拓扑荷数为m的相位奇点,物镜系统满足正弦条件,则有
(6)
式中,f为聚焦系统的焦距.
对m=1的情形进行展开,利用式Richards-Wolf矢量衍射理论[15],推导出聚焦电场表达式为
式中:Jn(β)为n阶第一类贝塞尔函数;β=kr2sinθ.
由上式可以看出,在考虑光束的矢量性的情形下,线偏振的离轴相位奇点光束经过物镜系统聚焦后,焦点区域的聚焦光场的电场分布在3个分量上均不为零.对于y方向上的线偏振光束,聚焦光场中y方向上的分量对光场强度贡献最大.事实上,线偏振奇点光束的聚焦光场能量主要集中在入射的线偏振光束的偏振方向上.
图3(见下页)为一阶离轴相位奇点光束在焦平面上的光场强度分布.为了方便观察,以y方向上的线偏振光束为例,入射光束光斑尺寸为ω0的高斯光束,且相位奇点位于y轴上,相位奇点的离轴量为ys.由图3可以看出,光场强度分布关于相位奇点的离轴方向即y轴对称,在相位奇点的离轴方向上则失去对称性,焦平面上总的聚焦光场强度分布的对称性与入射光场强度分布的对称性保持一致.随着相位奇点离轴量的增加,聚焦光场分布在离轴方向上的不对称性愈发明显,并且当离轴量大到一定程度时,光强分布的空心暗斑将无法分辨,如图3(c)所示,聚焦场光强逐渐退化成月牙形亮斑.相位奇点离轴量的符号仅表示奇点离开光轴的方向,聚焦光场的暗核离轴方向与入射光场的相位奇点离轴方向一致.
以数值孔径NA=0.9的物镜为例,计算得到,对于一阶的离轴相位奇点光束,当相位奇点离轴量为0.1ω0时,聚焦光场的暗核偏离量为0.09λ,相位奇点离轴方向上光强最大值偏离光轴0.57λ.入射光场相位奇点离轴量为0.2ω0时,聚焦场的暗核偏离量为0.18λ,光强最大值偏离光轴0.52λ;离轴量为0.3ω0时,聚焦场的暗核偏离量为0.28λ,光强最大值偏离光轴0.49λ.基本上,聚焦光场的暗核偏离值与入射光场的相位奇点的离轴量近似成正比,聚焦光场的光强最大值随着相位奇点偏离光轴越远而逐渐向光轴靠近.当入射光场相位奇点的离轴值为-0.3ω0时,光场聚焦情形与离轴值为0.3ω0时刚好相反,如图3(c)和3(d)所示.
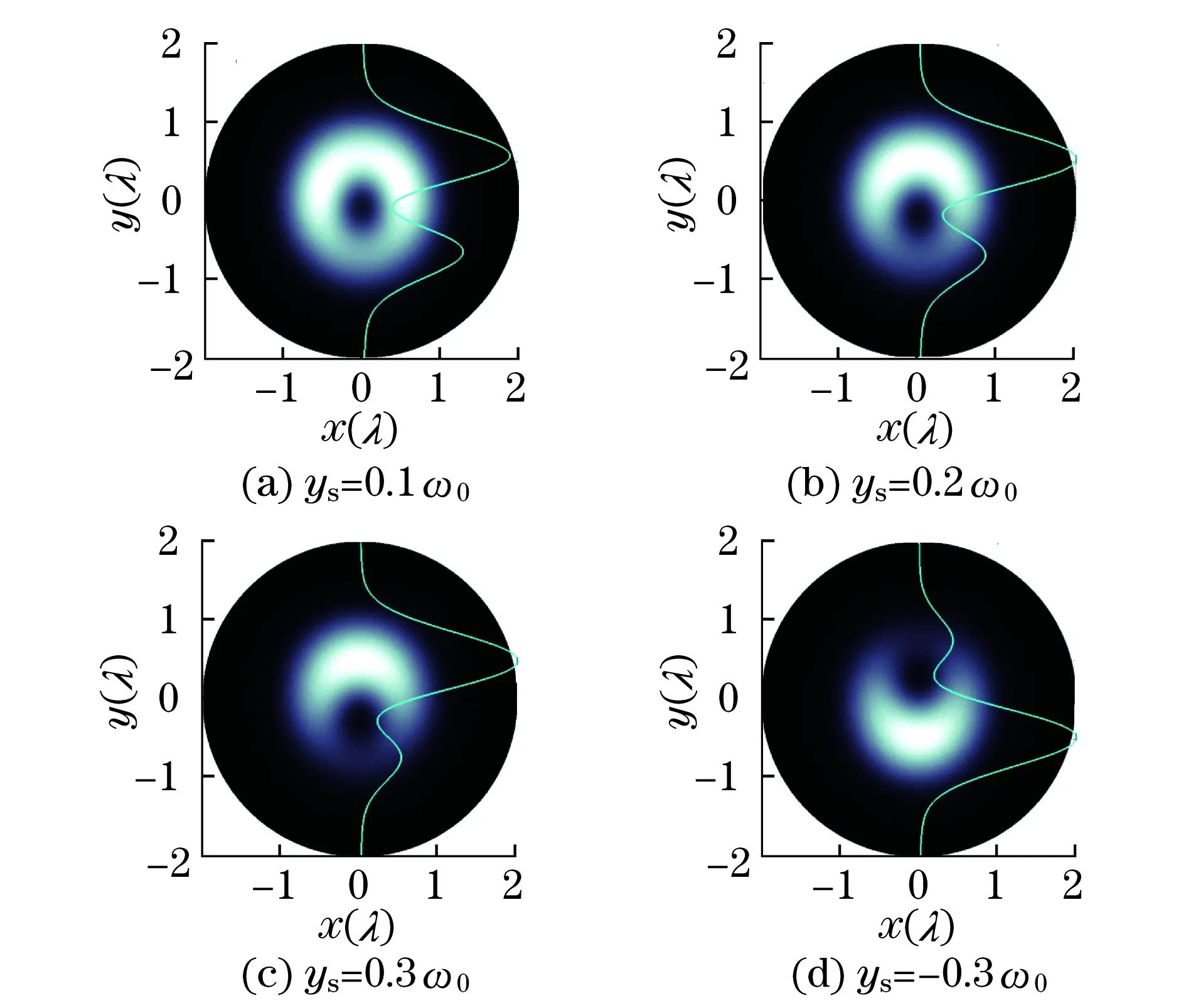
图3 离轴相位奇点焦平面上的光场强度分布
高阶离轴相位奇点光束的聚焦特性与一阶情形类似,聚焦光场强度分布仍关于相位奇点的离轴方向对称.奇点离轴越远,聚焦场光强最大值越靠近光轴,但相比一阶离轴相位奇点光束而言,在相同的离轴量下,涡旋拓扑荷数越大,聚焦光场的暗场也越大,即暗斑尺寸越大.由于线偏振光束经物镜聚焦后的光场分布主要取决于线偏振方向上的分量,为了更加详细地讨论高阶离轴相位奇点的聚焦场光强以及相位分布,单独分析入射偏振方向上的聚焦场分量,即y方向分量(以y方向线偏振高斯光束为例).图4为y方向线偏振高阶离轴相位奇点光束在焦平面上电场y分量的强度分布.
与一阶离轴相位奇点光束类似,高阶离轴相位奇点光束的聚焦光场在相位奇点的离轴方向上失去对称性,变化趋势与入射光场的强度分布一致.同一阶离轴相位奇点光束的聚焦场相比,和预期一样,高阶离轴相位奇点光束在焦平面上的光强分布暗斑尺寸更大,同时光场强度的最大值也会向着相位奇点的偏离方向移动.同样,当入射光场的相位奇点的偏移量足够大时,聚焦场的空心特性不再显著,即暗场斑表现不明显.如图4(f)所示,当ys= 0.2ω0,m=4时,空心亮环的下半部分光强已十分微弱,总的聚焦光场强度分布逐渐退化成月牙形.对于不同拓扑荷数的离轴相位奇点光束,聚焦光场的空心特性消失的位置也各不一样.拓扑荷数越大,相位奇点逐渐偏离光轴时,聚焦场强度分布的空心特性也会越早消失.

图4 高阶离轴相位奇点光束的聚焦场y分量光强分布
事实上,线偏振的高阶相位奇点光束在焦平面上沿着入射光场偏振方向上的电场分量的相位奇点会发生裂变,数量为入射光束的涡旋拓扑荷数,如图5(a)和5(b)所示.二阶的相位奇点在光轴上的涡旋光束在焦平面上其相位奇点会沿着x轴方向分裂成两个,并且关于原点对称,位于(±0.18λ,0)处.而当m=3时,聚焦光场的相位奇点沿x轴裂变成3个,其中一个位于原点上,另外两个相位奇点则关于原点对称,分别位于(-0.32λ,-0.02λ)和(0.32λ,-0.02λ)处,可以发现相位奇点在y轴上的偏移量非常微小.对于涡旋拓扑荷数为m的高阶离轴相位奇点光束,聚焦场偏振方向分量上光场的相位奇点同样裂变成m个.如图5(c),(d),(e)和(f)所示,当m=2,ys= 0.1ω0时,相位奇点关于y轴对称,分别位于坐标(-0.165 2λ,-0.071 5λ)和(0.165 2λ,-0.071 5λ)处.在离轴情形下,分裂的相位奇点位置与非离轴情形下相比,略微向离轴方向上有所偏移,但离轴量保持不变.计算表明:当入射光场的相位奇点离轴量更大时,聚焦场的相位奇点也越来越远离x轴,但在沿着x轴方向上偏移量变化并不大;当m=3,ys= 0.1ω0时,聚焦光场y方向上分量的相位奇点分别位于原点和(±0.32λ,-0.115 2λ)处.对于y方向上的高阶离轴相位光束的聚焦光场,分裂相位奇点在位置上关于y轴对称,聚焦光场的波前位错线向着入射光束相位奇点的偏离方向弯曲,并且随着相位奇点偏离量的增大,波前位错线弯曲程度也越大,如图5(e),(f)所示.

图5 高阶离轴相位奇点光束的聚焦场y分量相位分布
上述高阶离轴相位奇点光束的聚焦光场的相位奇点的对称性,仅在入射光场的相位奇点离轴方向与偏振方向一致的情况下保持.当相位奇点的离轴方向与入射线偏振光的偏振方向不同时,分裂的相位奇点将失去对称性.通过更为详细的计算,发现高阶的相位奇点光束在衍射传播过程中相位奇点会自然发生分裂.在低数值孔径物镜系统下,线偏振光束偏振方向上的聚焦光场分量的相位奇点分裂将更加明显,即相位奇点的裂变并不是由于光束的紧聚焦引起的,物镜系统的数值孔径大小仅影响裂变相位奇点的离轴量大小.但由于低数值孔径物镜系统聚焦下的光斑尺寸较大,光场能量比较分散,在应用价值上一般不如紧聚焦光场.
2 对称双涡旋离轴相位奇点光束
高阶的线偏振相位奇点光束经过物镜系统聚焦后,其偏振方向分量上的聚焦光场的相位奇点会发生裂变,裂变数与相位奇点的阶数相等,即高阶的线偏振光束的衍射聚焦光场在其偏振方向分量上的光场退变成了一阶的多相位奇点光束.本文以对称双涡旋相位奇点光束为例,直接讨论多相位奇点光束的传播特性.这里仅讨论两个相位奇点的情况,对于y方向上的线偏振高斯光束,双涡旋拓扑荷数值为m1和m2的光学涡旋分别嵌于点(ρs1,φs1),(ρs2,φs2)处,入瞳平面上电场分布可表示为
对于对称分布的双涡旋相位奇点光束,ρs1=ρs2,φs2=φs1+π,于是上式可简化成
而当两个相位奇点的涡旋拓扑和数值m1=m2时,可进一步化简为
(10)
为了不失一般性,仍以φs=π/4为例.当m=1时,不同离轴量下的高斯相位奇点光束的光场强度分布和波前相位分布如图6所示(见下页).

图6 高斯对称双离轴相位奇点光束的光强和相位分布
当ρs=0.1ω0时,光场强度如图6(a)所示,由于离轴相位奇点会将光斑中心往反向离轴方向挤压,对称双涡旋叠加后会导致光强最大值有两个,对称分布在相位奇点连线段的中垂线上,离轴距离为0.99ω0;当ρs=0.2ω0时,光强最大值的离轴量为0.98ω0;当ρs=0.3ω0时,光强最大值离轴量为0.95ω0;当ρs=0.5ω0时,光强最大值的离轴量为0.87ω0.随着相位奇点的离轴距离越来越大,光场强度的最大值也会越来越靠近原点,同时光束中心的光场强度值也会越来越大.由图6可以发现,当相位奇点的离轴量很小时,从光强分布上无法区分出两个暗核,类似于相邻两个亮斑的可区分判定,当光场中心即原点处的光强值小于光强最大值的1/e的时候,认为相位奇点处的两个暗斑无法区分.对于对称的双涡旋相位奇点高斯光束,当相位奇点的离轴距离小于0.4ω0,即两相位奇点相距小于0.8ω0时,光强分布的两个暗斑无法区分,近似表现为面包圈型的中空光束.随着相位奇点的离轴距离增大,两个暗斑将越来越明显,当相位奇点离轴量大于0.75ω0,即两相位奇点相距大于1.5ω0时,光场强度分布的暗斑逐渐消失,呈腰鼓状分布.当涡旋拓扑荷数增大时,相位奇点所影响的范围也越大,即暗斑尺寸越大,对应的涡旋核暗斑判据可类似一阶对称涡旋相位奇点光束得到.
同样,利用矢量衍射理论,对对称双涡旋相位奇点光束得聚焦光场进行数值模拟,与单离轴相位奇点光束一样,研究相位奇点位于偏振方向上的线偏振光束.当m=1,相位奇点离轴量为±ys时,入射的双涡旋相位奇点光束经物镜系统聚焦后在焦点区域的电场分布为
其中,l0(θ)为入射的对称双涡旋相位奇点光束在入瞳面处的电场分布,其表达式为
(12)
于是式(11)可化简为
物镜数值孔径取0.9,图7为不同离轴量下的对称双涡旋相位奇点光束在焦平面上的光场强度分布.
可以看出,在紧聚焦情况下,相位奇点离轴距离大于0.46ω0时,聚焦场暗斑开始分离,左右两边的亮斑逐渐靠近变得不可分辨,如图7(d)所示.当ys=ω0时,相位奇点光束在焦平面上的聚焦光场强度分布已退化成一个偏平亮斑.可以看出,对称双涡旋相位奇点光束紧聚焦后的光强分布与入射光场强度分布类似,但由于紧聚焦的作用,光斑能量更为集中,光强分布随着相位奇点离轴量的增大而变化得更迅速.
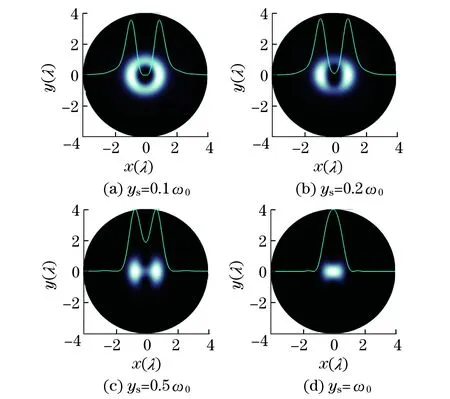
图7 对称双涡旋相位奇点光束的焦场分布
3 结 论
根据涡旋相位奇点对光场分布的影响,给出了普遍的具有离轴相位奇点的高斯光束电场表达式,基于Richards-Wolf的矢量衍射理论,对线偏振的离轴相位奇点光束的聚焦光场进行了数值分析.结果表明:相位奇点的离轴量将影响光强整体分布,光场强度的最大值向相位奇点偏离方向靠近;高阶的相位奇点光束在聚焦场会出现相位奇点裂变;具有对称双涡旋相位奇点的高斯光束的电场强度分布在奇点偏离方向上以及奇点连线段的中垂线上对称,光场强度的最大值受两边相位奇点影响出现在奇点连线段的中垂线上;离轴涡旋光束的拓扑荷数对光斑暗场尺寸的影响与普通涡旋光束一致.
[1] WRIGHT E M,ARLT J,DHOLAKIA K.Toroidal optical dipole traps for atomic bose-einstein condensates using laguerre-gaussian beams[J].Physical Review A,2000,63(1):013608.
[2] ZHANG D W,YUAN X C.Optical doughnut for optical tweezers[J].Optics letters,2003,28(9):740-742.
[3] ASHKIN A.Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime[J].Biophysical Journal,1992,61(2):569.
[4] SIMPSON N B,ALLEN L,PADGETT M J.Optical tweezers and optical spanners with Laguerre-Gaussian modes[J].Journal of Modern Optics,1996,43(12):2485-2491.
[5] GAHAGAN K T,SWARTZLANDER G A.Optical vortex trapping of particles[J].Optics Letters,1996,21(11):827-829.[6] BEIJERSBERGEN M W,ALLEN L,VAN V H,et al.Astigmatic laser mode converters and transfer of orbital angular momentum[J].Optics Communications,1993,96(1):123-132.[7] BAZHENOV V Y,VASNETSOV M V,SOSKIN M S.Laser beams with screw dislocations in their wavefronts[J].Jetp Lett,1990,52(8):429-431.
[8] HECKENBERG N R,MCDUFF R,SMITH C P,et al.Generation of optical phase singularities by computer-generated holograms[J].Optics Letters,1992,17(3):221-223.[9] ROUX F S.Diffractive optical implementation of rotation transform performed by using phase singularities[J].Applied Optics,1993,32(20):3715-3719.
[10] BEIJERSBERGEN M W,COERWINKEL R P C,KRISTENSEN M,et al.Helical-wavefront laser beams produced with a spiral phaseplate[J].Optics Communications,1994,112(5):321-327.
[11] TUMBULL G A,ROBERTSON D A,SMITH G M,et al.The generation of free-space laguerre-gaussian modes at millimetre-wave frequencies by use of a spiral phaseplate[J].Optical Angular Momentum,2003:186.
[12] CURTIS J E,GRIER D G.Modulated optical vortices[J].Optics Letters,2003,28(11):872-874.
[13] VAUGHAN J M,WILLETTS D V.Interference properties of a light beam having a helical wave surface[J].Optics Communications,1979,30(3):263-267.
[14] ORON R,DAVIDSON N,FRIESEM A A,et al.Efficient formation of pure helical laser beams[J].Optics Communications,2000,182(1):205-208.
[15] RICHARDS B,WOLF E.Electromagnetic diffraction in optical systems.II.Structure of the image field in an aplanatic system[C]∥Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences.The Royal Society,1959,253(1274):358-379.
(编辑:董 伟)
Properties of Linearly Polarized Gaussian Beams with Off-Axis Phase Singularities
XU Jianghua, ZHUANG Songlin
(SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceand
The particular properties of off-axis vortex beams which have off-axis singularities in the phase fronts of laser beams were explored.The expression of the electric distribution of off-axis vortex beams and their focusing characters were studied.The superposition of off-axis singularities can cause an asymmetric intensity distribution.Also,it offers another choice of the generation of non-uniform intensity distributions.
phasesingularity;vortexbeam;singularityopticalbeam;off-axissingularity;intensitydistribution
1007-6735(2016)06-0527-08
10.13255/j.cnki.jusst.2016.06.004
2016-05-04
国家973计划资助项目(2015CB352001)
许江华(1989-),男,博士研究生.研究方向:奇点光学.E-mail:fattyguy@sina.com
庄松林(1940-),男,教授,研究方向:光学工程.E-mail:slzhuang@163.com
O 43
A

