校园标志物空间形态的测量与分析

郭雪瑶，田林亚，黄　瑾，邓　旭

(河海大学地球科学院与工程学院，江苏 南京 210098)

GUO Xueyao，TIAN Linya，HUANG Jin，DENG Xu

校园标志物空间形态的测量与分析

郭雪瑶，田林亚，黄瑾，邓旭

(河海大学地球科学院与工程学院，江苏 南京 210098)

Measurement and Analysis of Campus Landmark’s Spatial Form

GUO Xueyao，TIAN Linya，HUANG Jin，DENG Xu

摘要：研究了利用免棱镜全站仪进行建筑物形态测量与分析的方法，重点研究了坐标系转换、非线性拟合、形态分析等关键问题。以校内标志物——混流式水轮机转轮为研究对象，利用免棱镜全站仪采集了该物体形态特征点的三维坐标，通过空间平面拟合完成了水轮机转轮的平整度计算与分析，通过坐标转换和平面拟合进一步完成了水轮机转轮圆心坐标、圆半径和圆度的计算与分析。研究和试验表明，利用免棱镜全站仪进行水轮机转轮的空间形态测量是一种快捷和精密的方法，该方法可为其他类似建筑物的空间形态测量提供一定的参考，空间形态测量的数据处理和方法也将得到更加深入的研究。

引文格式： 郭雪瑶，田林亚，黄瑾，等. 校园标志物空间形态的测量与分析[J].测绘通报，2015(9)：87-90.DOI:10.13474/j.cnki.11-2246.2015.0287

关键词：免棱镜全站仪；水轮机转轮；形态测量；坐标系转换；非线性拟合；形态分析

中图分类号：P258

文献标识码：B

文章编号：0494-0911(2015)09-0087-04

收稿日期：2014-10-24

基金项目：精密工程与工业测量国家测绘地理信息局重点实验室开放基金(PF2012-3)；河海大学生创新创业训练项目(2013102941088)

作者简介：郭雪瑶(1993—)，女，研究方向为精密工程测量。E-mail: 675812210@qq.com

一、引言

物体形态测量是从工业上一些精密部件三维尺寸和形状参数的测量开始的，在工业精密制造、安装与检测领域具有广泛的应用。随着科学技术、工程与工业设计、施工工艺等的进步，物体的种类、大小和形态越发多样化，针对小型物体形态的测量仪器和方法已经不能满足要求，全站仪法、近景摄影仪法、激光跟踪仪法、激光扫描仪法等相继得到研究和应用。

全站仪测量方法虽然只能获得物体形态的点状数据，但方法简单、投资少，特别适用于大型物体的形态测量，已在许多物体的形态测量中得到研究和应用。全站仪用于物体形态测量具有大范围、高精度、非接触等特点，其数据处理和分析系统的研究与开发成果也可以推广应用到大型工程建构筑物的施工测量，以及大型工业产品的制造、安装与检测中[1]。

本文研究了利用免棱镜全站仪进行建筑物形态测量与分析的方法，重点研究了坐标系转换、非线性拟合、形态分析等关键问题，以笔者所在院校混流式水轮机转轮作为研究对象，利用高精度免棱镜全站仪采集了水轮机转轮上若干特征点的三维坐标，根据水轮机转轮的空间形态数学模型和非线性拟合方法编写了计算程序，完成了水轮机转轮的空间形态分析。

二、研究的技术路线

混流式水轮机是反击式水轮机中的一种，是水电厂将水能转换为机械能的重要设备，水轮机外形的特性曲线在不同工况下用于表达其对水流能量的转换及空化方面的水力特性。本文中混流式水轮机转轮原为新安江水电站4号水轮机转轮，转轮机的叶片数为14片，剖面形状为空间圆形，如图1所示。

利用免棱镜全站仪对水轮机转轮进行空间形态测量与分析的技术路线如图2所示。首先研究水轮机转轮空间形态的表达形式和分析方法，利用免棱镜全站仪自由设站法对水轮机外环的特征点进行三维坐标的数据采集；然后直接采用特征点的三维坐标进行空间平面的拟合和平整度计算；最后经过测量坐标系与物方空间坐标系的转换，建立平面圆的拟合方程计算空间圆的圆心坐标、圆半径和圆度。整个计算与分析通过C#语言编程实现。

图1　水轮机转轮

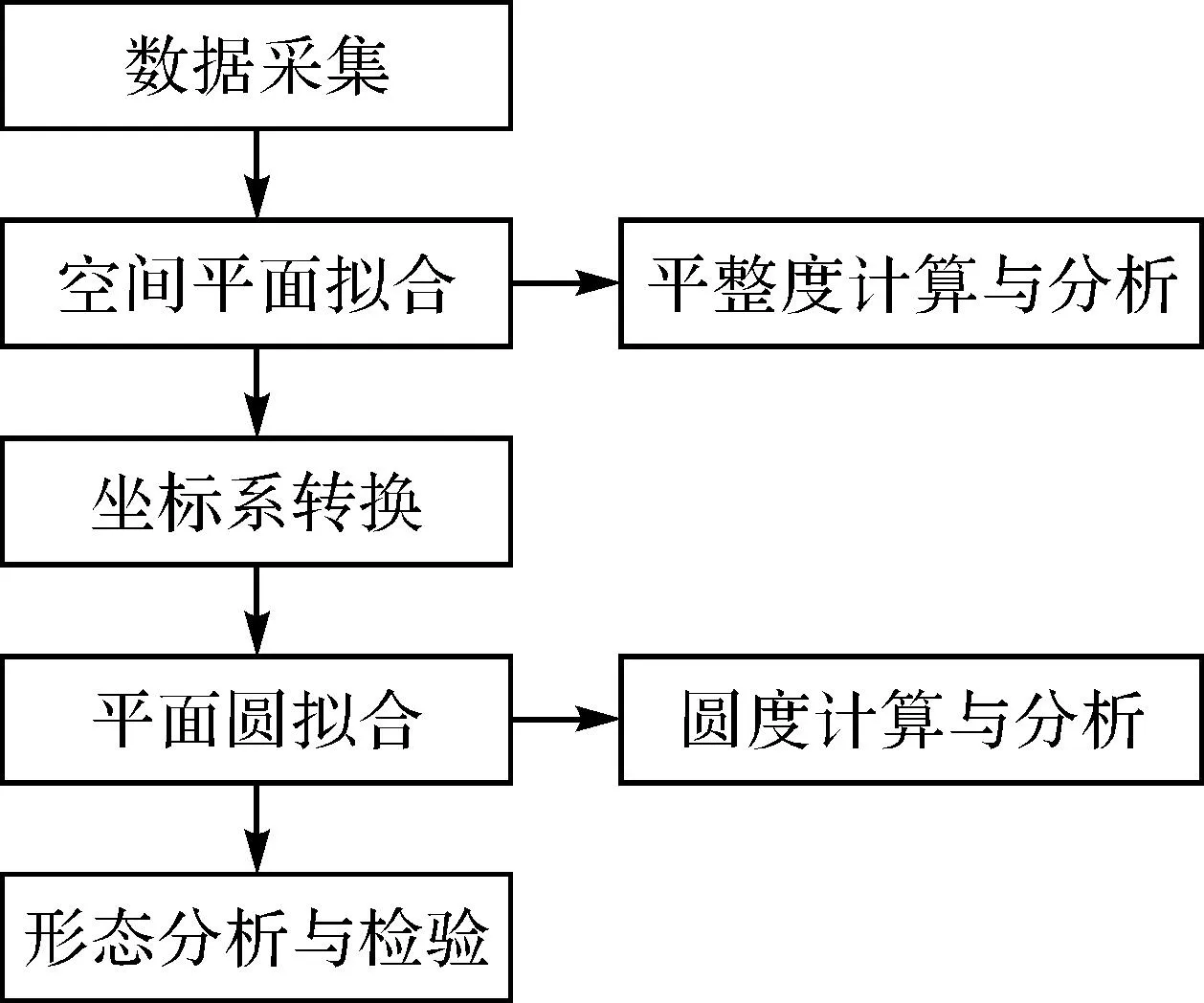
图2　研究的技术路线

三、水轮机转轮特征点的数据采集

采用免棱镜全站仪自由设站的方法进行特征点坐标的数据采集，也就是将测站点视为测量坐标系的原点，任意确定方向后对水轮机转轮外环的24个特征点进行三维坐标测量，再将测量数据从全站仪中导出，制成表格以便于计算和分析。24个特征点的原始测量数据见表1，24个特征点的三维分布如图3所示。

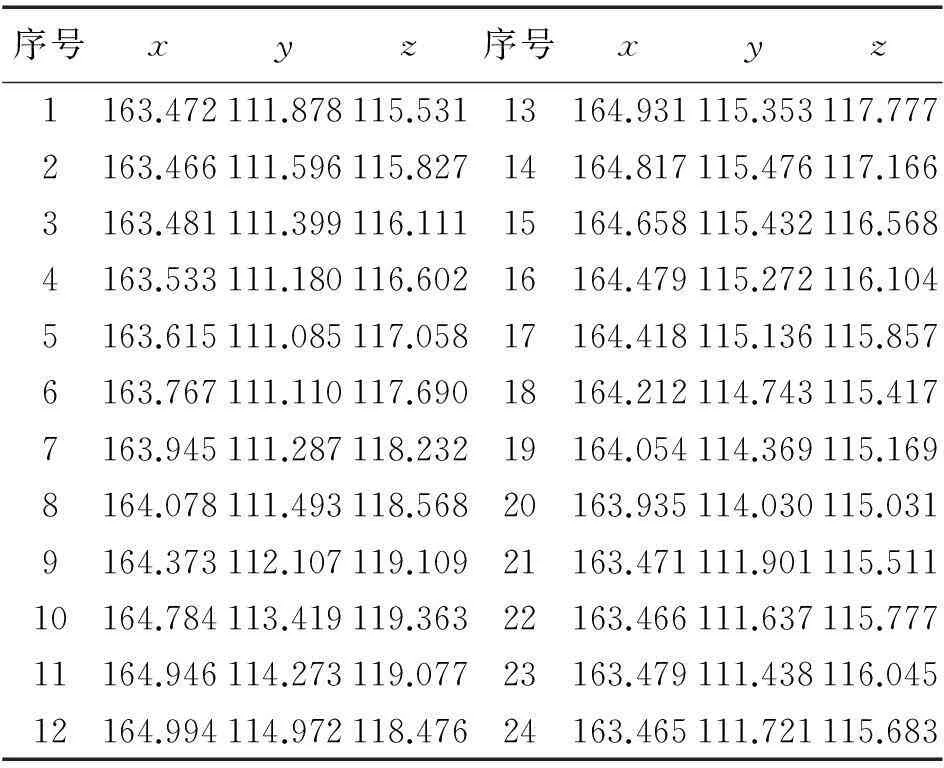
表1　原始测量数据　m

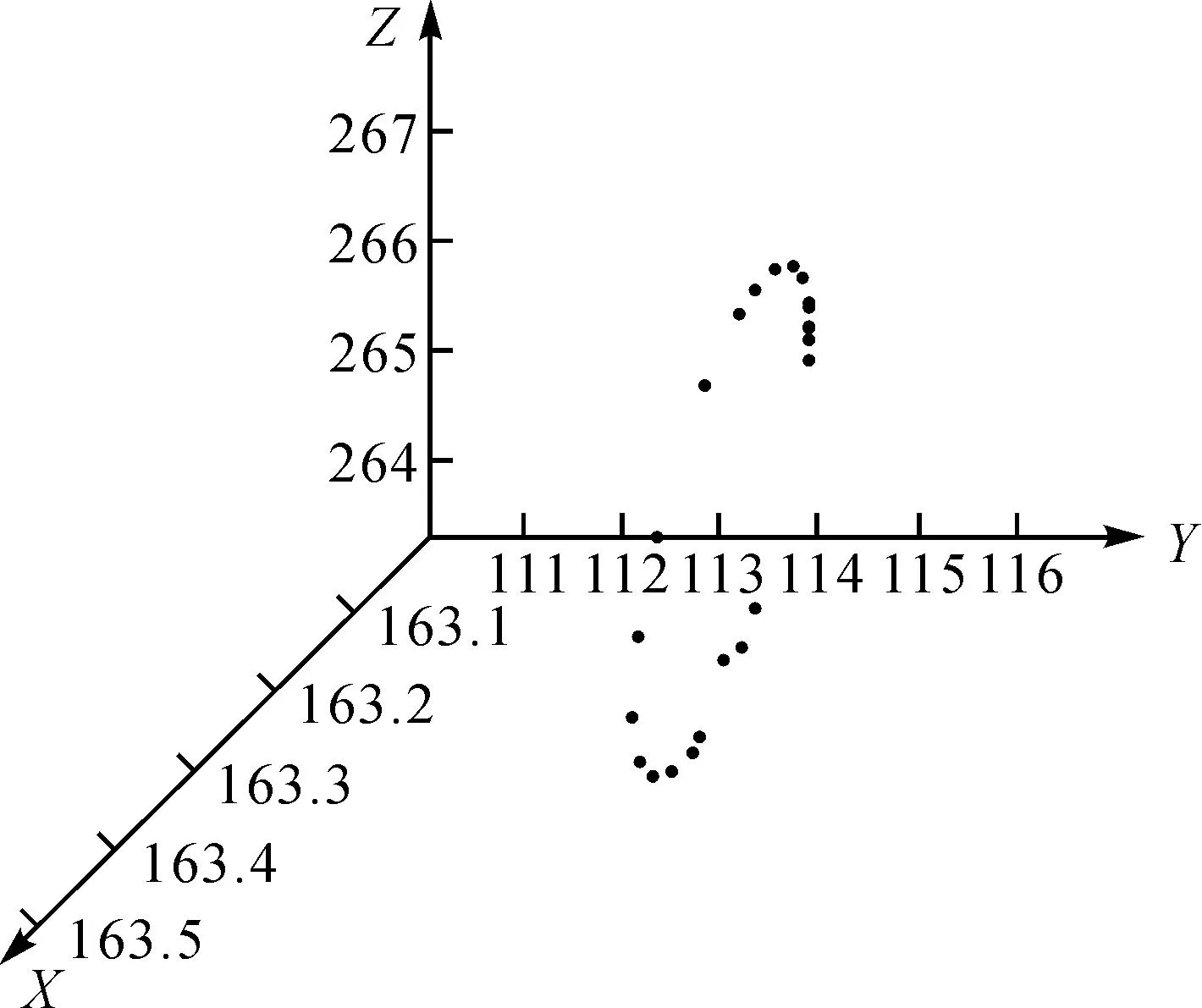
图3　特征点的三维分布

四、水轮机转轮空间形态的计算与分析

1. 空间平面拟合与平整度计算

根据空间几何理论，空间三维坐标系中平面的方程[2]为

Ax+By+Cz-D=0

(1)

A、B、C、D这4个参数存在着线性关系，可以求得无数组解，因此令D=1，则可以求出固定解，此时的空间平面不经过原点[3]。空间平面方程为

ax+by+cz-1=0

(2)

式(2)用误差方程[4]的形式表示为

v=Qx-l

(3)

各个特征点到该平面的垂直距离Δd可以用来表达空间平面的平整度[4-5]，Δd的计算公式为

(4)

由此得到该拟合平面的法向量为(0.942 259 64，-0.251 224 807，-0.221 408 37)。各个特征点到拟合平面的垂直距离见表2。

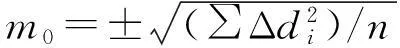
第i(i=1，2，…，n)个观测点在该平面内的投影坐标计算公式[7]为

(5)

各个观测点在该平面内的投影坐标见表3。

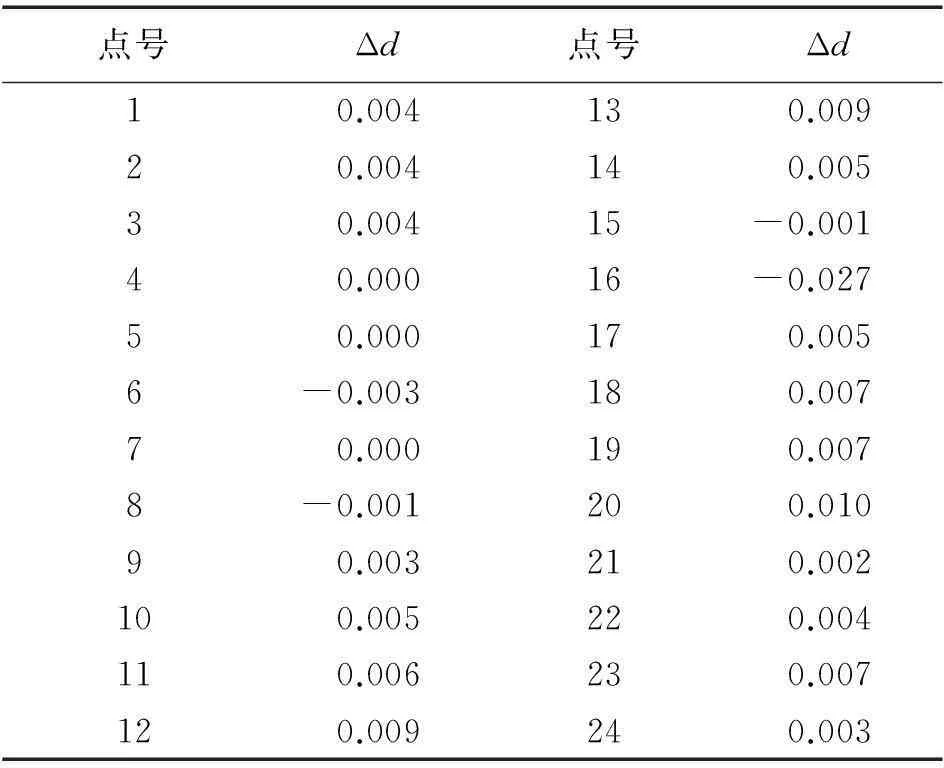
表2　各个特征点到拟合平面的垂直距离　m

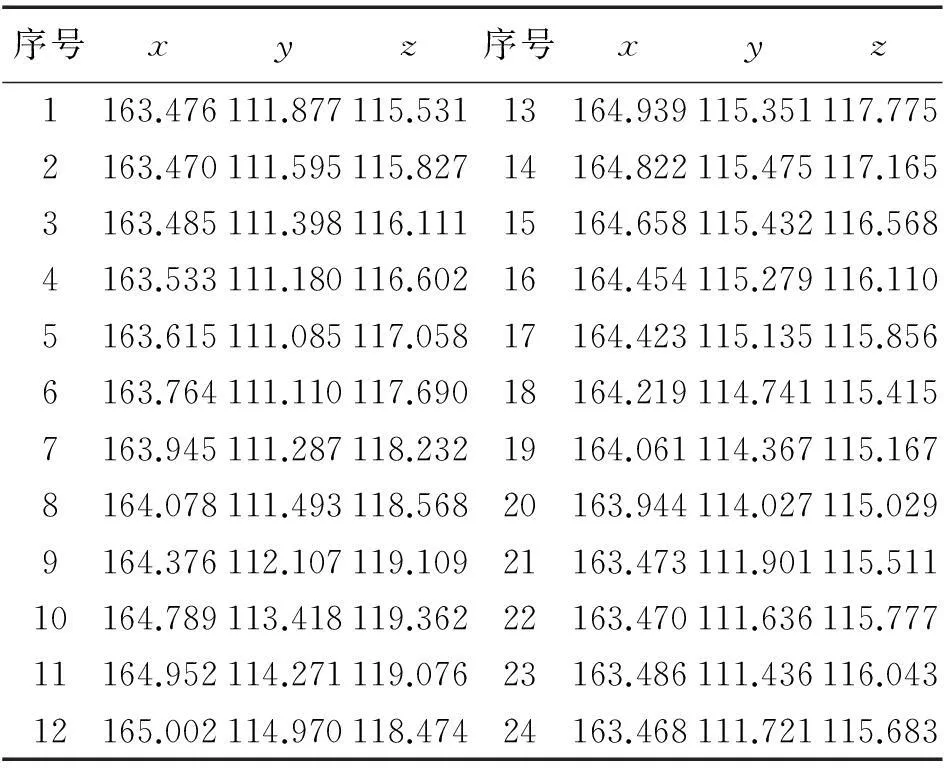
表3　投影后坐标　m

2. 空间三维坐标向二维平面坐标的转换

现场测量所得的点位坐标数据属于测量坐标系，与物方空间坐标系是不一致的，需要进行坐标系转换。由于任意两个空间直角坐标系之间通过平移、旋转、缩放进行相互转换需要求出3个平移参数、3个旋转参数和1个尺度参数共7个参数，至少要有3对公共点才能解算出转换参数，且物方空间坐标系中的公共点坐标是无法确定的，因此最简单的方法就是假设坐标原点不变，将拟合平面旋转到与xoy平面平行的位置后再建立坐标系，无须顾及坐标系的平移和缩放，只需要对测量坐标系进行一定角度的旋转即可。

如图4所示，设测量坐标系为oxyz，旋转一定的角度后转换到物方空间坐标系o′x′y′z′。设任意一点P在oxyz中的坐标为(x,y,z)，在o′x′y′z′中的坐标为(x′,y′,z′)。将空间圆所在的平面视为x′o′y′平面，其法方向视为z′轴方向，将z′轴方向旋转到与z轴方向平行的同时，空间圆所在的平面即可与xoy平面平行。由z轴和z′轴方向，可以计算出该任意旋转轴方向为n=[nxnynz]=[0.251 2250.942 260]，z′轴到z轴的旋转角为θ=102°47′31″，再根据以下公式可以计算出旋转矩阵[8]

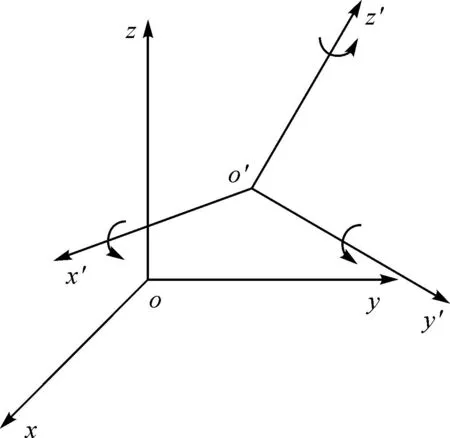
图4　坐标系转换

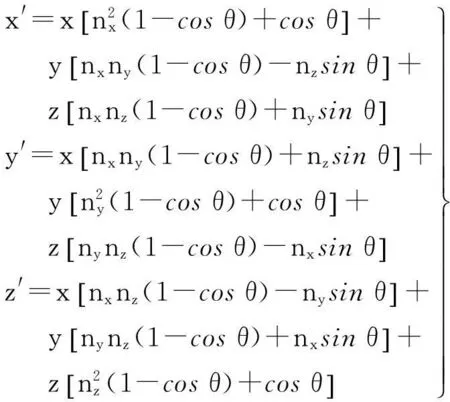
(6)

经计算得

将原始数据代入上式，可求得24个点在新坐标系中的坐标见表4。

从表4可以看出，在转换后的新坐标系中，这24个点的z′轴坐标近于相同，可以认为这些点在同一水平面上，可以将转换后的三维空间圆看成二维的平面圆，这样就大大降低了物体形态拟合和分析的难度。

表4　观测点在新坐标系中的坐标　m

3. 平面圆拟合与圆度计算

平面圆一般方程式为

(x-x0)2+(y-y0)2=R2

(7)

px+qy-r-(x2+y2)=0

(8)

对所有观测点(xi，yi)，列误差方程为

(9)

误差方程线性化[9]为

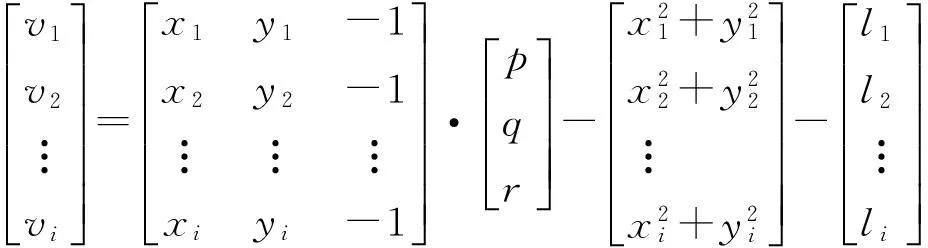
(10)

由于建立的物方空间坐标系中不涉及z方向，可以选取3个点的平面坐标(x1,y1)、(x2,y2)、(x3,y3)，按以下公式[10]计算圆心坐标和圆的半径

(11)

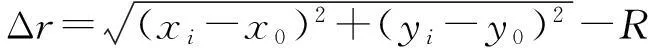
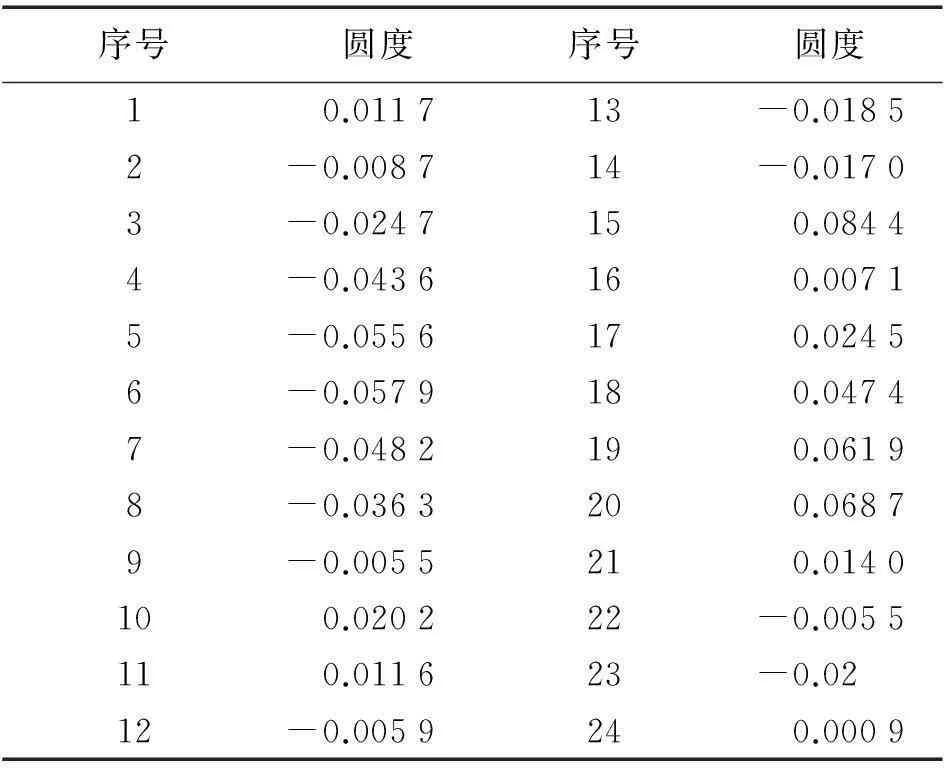
表5　圆度计算结果　m

圆度即通常所说的圆整程度，常作为评价圆形零件形状精度的重要指标之一。从表5数据可以得到，最大圆度为0.084 4 m，最小圆度为0.000 9 m，说明该转轮个别部位的圆整程度已经发生了较大的变化。

五、结论

本文利用免棱镜全站仪对笔者所在院校混流式水轮机转轮进行了特征点的数据采集，研究了水轮机转轮空间形态的分析方法，结合实测数据进行计算与分析，得到以下结论：

1) 采用免棱镜全站仪进行物体形态特征点的数据采集，方法简单快捷，精度较高。选取特征点时，应使点位大致均匀分布，具体数量视空间物体形态的大小而确定。

2) 平面的拟合方法有多种，本文直接采用测量所得的三维坐标进行空间平面的拟合，方法简便，思路清晰，能够快速有效地拟合出空间平面，并计算出平整度。

3) 将测量坐标转换成物方空间坐标的方法是本文的创新点之一，通过坐标系的旋转可以将三维的空间圆旋转成为二维的平面圆，这样更方便于圆的拟合和分析，大大降低了空间圆拟合的难度。运用迭代法进行圆形拟合，可以更精确地求得圆心坐标和半径。

4) 本次研究主要针对空间圆形物体进行形态测量与分析，今后还将深入研究和建立多种物体空间形态的数学模型，研究多种物体空间形态的分析、仿真与可视化方法。

参考文献：

[1]葛世超. 大型建(构)筑物形体测量与数据处理研究[D].南京:河海大学, 2005.

[2]张益泽, 王解先. 建筑物的平面拟合和质量检测[J].工程勘察,2011(9):79-81,86.

[3]潘国荣, 谷川, 施贵刚. 空间圆形物体检测方法与数据处理[J].大地测量与地球动力学,2007,27(3):28-30.

[4]田晓, 李全海. 基于投影点的空间圆形拟合检测新方法[J].工程勘察,2014(5):72-74.

[5]赵士华. 工业安装测量与检测技术研究及应用[D].南京：河海大学,2006.

[6]程效军, 唐剑波. 基于最小二乘你喝的墙面平整度检测方法[J].测绘信息工程,2007,32(4):19-20.

[7]杨丽, 楼立志. 用拟合方法检测空间圆形物体的变形[J].铁道勘察,2009(4):47-49,61.

[8]薛文风.三维空间坐标的旋转算法[J].电脑编程技巧与维护,1995(6):59-60.

[9]谷川, 杨元伟. 圆形盾构隧道断面自动化检测系统研究与开发[J].城市道桥与防洪, 2011(10):148-151,161.

[10]周扬眉. 精确测定圆形物体中心位置的方法[J].岩土工程技术,1999(2):56-58.

[11]朱陶业,朱建军,张学庄等.大气折射的映射函数与神经网络拟合比较分析[J]. 测绘学报，2007 , 36 (3): 290-301.

[12]张春森, 郑艺惟, 黄小兵,等.视频测量影像序列椭圆形人工目标点快速识别和跟踪方法[J]. 测绘学报， 2015, 44 (8): 909-918.