地表面积计算方法研究

韩买侠，程传录，王　维

(国家测绘地理信息局大地测量数据处理中心, 陕西 西安 710054)

HAN Maixia，CHENG Chuanlu，WANG Wei

地表面积计算方法研究

韩买侠，程传录，王维

(国家测绘地理信息局大地测量数据处理中心, 陕西 西安 710054)

Research on the Calculation Method of Surface Area

HAN Maixia，CHENG Chuanlu，WANG Wei

摘要：通常面积是指地图上的面积，而地理国情监测中面积是指地表面积，即实际面积。地表面积计算涉及坐标换算、投影、积分问题，计算复杂，本文研究了地表面积计算的理论，分析了影响地表面积计算精度的因素，确定了地表面积计算的方法步骤，并利用实际数据对该计算方法进行了验证，取得了良好的效果。

引文格式： 韩买侠，程传录，王维. 地表面积计算方法研究[J].测绘通报，2015(9)：72-74.DOI:10.13474/j.cnki.11-2246.2015.0283

关键词：地表面积；地理国情监测；图斑面积；计算方法

中图分类号：P237

文献标识码：B

文章编号：0494-0911(2015)09-0072-03

收稿日期：2014-08-01

作者简介：韩买侠(1963—)，女，高级工程师，主要从事数据库设计及4D产品坐标转换方法研究。E-mail：hmxmaill@163.com

一、引言

目前我国正在实施的地理国情监测项目就是综合利用全球导航卫星系统、航空航天遥感技术、地理信息系统技术等现代测绘技术，综合各时期测绘成果档案资料，对自然地理要素或地表人工设施要素等进行动态和定量化、空间化的监测，并统计分析其变化量、变化频率、分布特征、地域差异、变化趋势等，形成反映各类资源、环境、生态、经济要素的空间分布及其发展变化规律的监测数据、地图和研究报告等，从地理空间的角度客观、综合展示国情国力。地理国情监测中的一项重要内容是统计计算面状要素的地表面积。由于三维地形是随机起伏的，因此在这个面域内三维地形的表面也是随机高低起伏的[1]，在计算面状要素地表面积时，需要结合地形起伏的高程数据才能得到实际地表面积。

本文使用数字高程模型(DEM)和似大地水准面模型实现地表三维空间几何恢复，将地表覆盖的任意区域按DEM分辨率分为整格网与非整格网，对整格网和非整格网的地表面积计算方法分别进行了研究，分析了影响地表面积计算精度的因素。

二、基本原理

1. 地表面积定义

地理国情监测项目地形表面区域面积是指面要素沿地球表面累计的面积。在实际计算过程中以2000国家大地坐标系参考椭球为基础，并考虑实际地形起伏下沿地球表面积累的植被覆盖(面)、水系(面)、行政区划单元(面)等面状要素的面积。

2. 地表三维空间几何模型恢复

DEM是通过有限的地形高程数据实现对地形曲面的数字化模拟(即地形表面形态的数字化表示)，反映了地表形态空间地理信息，DEM数据是采用二维平面坐标附加正常高高程实现的一种三维空间地理信息。在计算地形表面区域面积时，可以使用DEM正常高和似大地水准面模型中恢复地形表面的三维空间几何模型，如图1所示。

1) 将高斯平面坐标(x,y)反算为大地坐标(B,L)[2]。

2) 大地高(H)=正常高(h)+高程异常(ζ)[2]。

3) 将B、L、H换算为空间直角坐标X、Y、Z[2]。

图1　地形在不同参考基准下的表达

3. 地形表面理论面积

地形表面区域面积是指面要素沿地形表面积累的面积。在空间直角坐标系下，沿地表区域对面积微元进行累加计算(如图2所示)，即可获得地形表面区域面积，即

式中,ds是沿地表区域的面积微元。

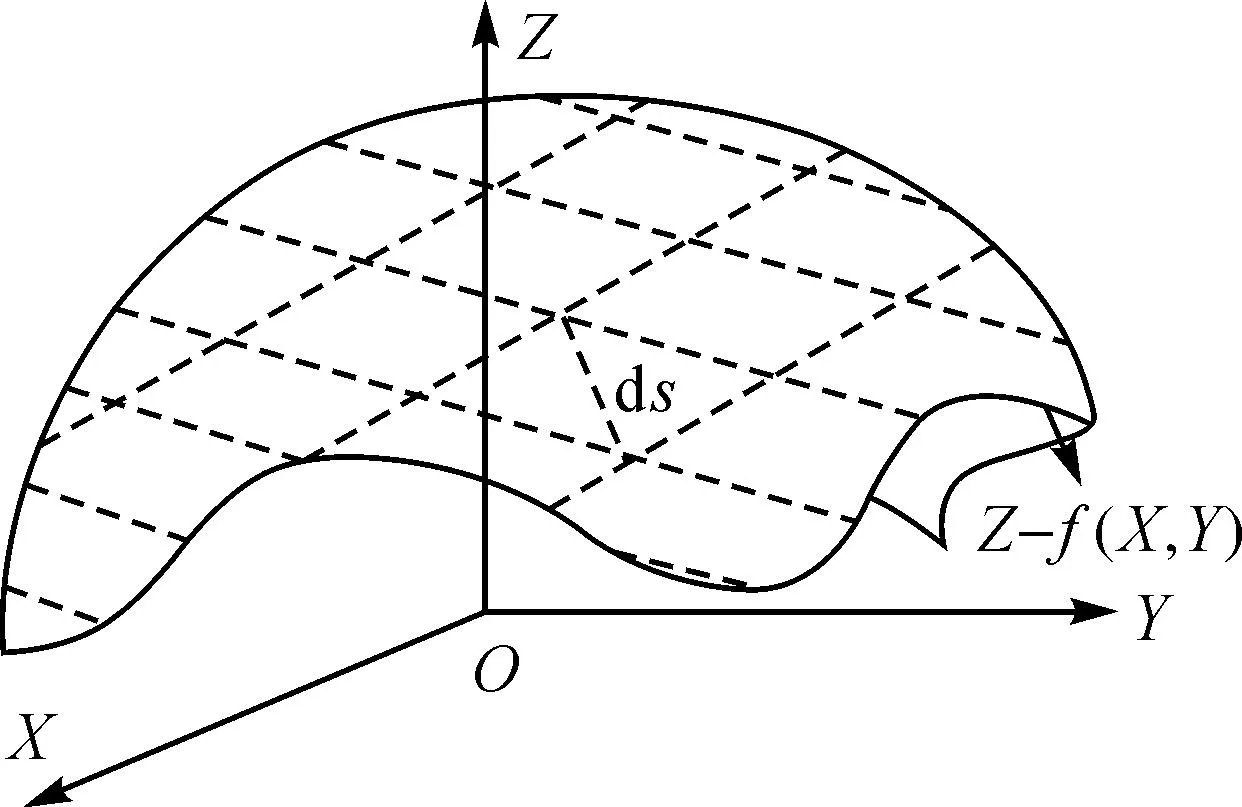
图2　地表面积微元计算

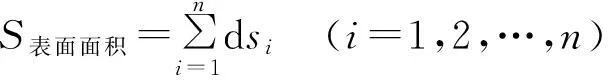
三、地表区域面积计算方法

DEM数据有多种分辨率，不同分辨率DEM数据计算同一区域地形表面区域面积不同。理论上，DEM分辨率越高，计算的地形表面区域面积越接近真实值，但DEM分辨率越高计算地形表面区域面积效率越低。以1∶10 000比例尺DEM(分辨率为5 m)为基础，计算任意区域地表面积方法如下：

1) 对于任意封闭区域(如图3所示)，读取范围，再按DEM分辨率对封闭区域范围外扩一个像素。

2) 根据封闭区域外扩范围，计算覆盖的DEM最大行列数(Row,Col)。

3) 根据范围最小值及行列数，生成Row×Col个封闭矩形区域(如图4所示)。

4) 根据生成封闭矩形4个角点坐标，读取所在DEM正常高，根据地表三维空间几何模型恢复方法，换算为空间直角坐标(X，Y，Z)。

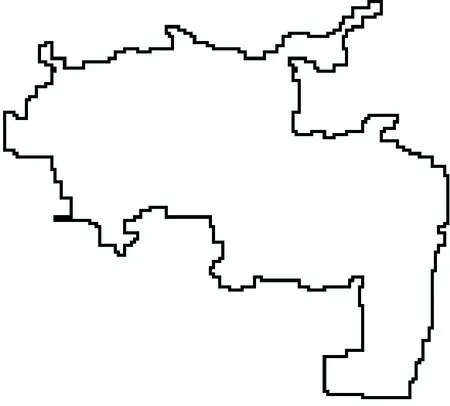
图3　任意封闭区域

图4　封闭矩形区域

5) 计算图3、图4交集[3-5]得图5，在图5中包含大量的整格网(阴影)和非整格网(非阴影)。分别计算整格网和非整格网的面积，累加得到要素地表面积。

6) 整格网地表面积计算：基于整格网构建4个三角形(如图6所示)，由海伦定理(即式(1))计算三角形地表面积[6]，三角形如图7所示。

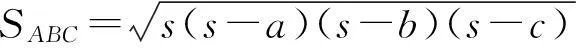
(1)

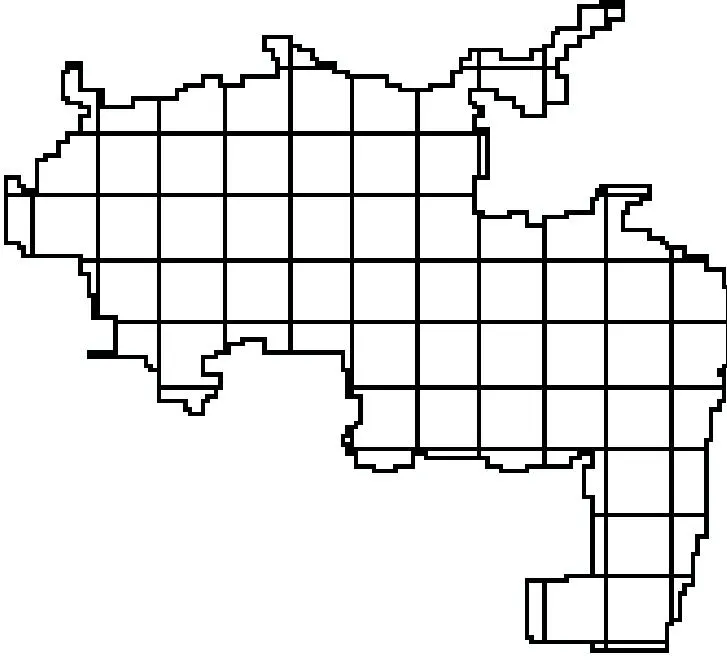
图5　封闭区域与封闭矩形交集

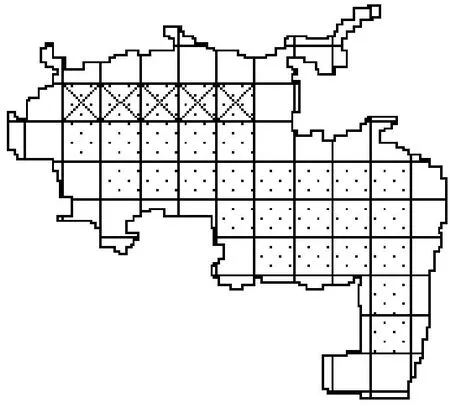
图6　整格网构建三角形

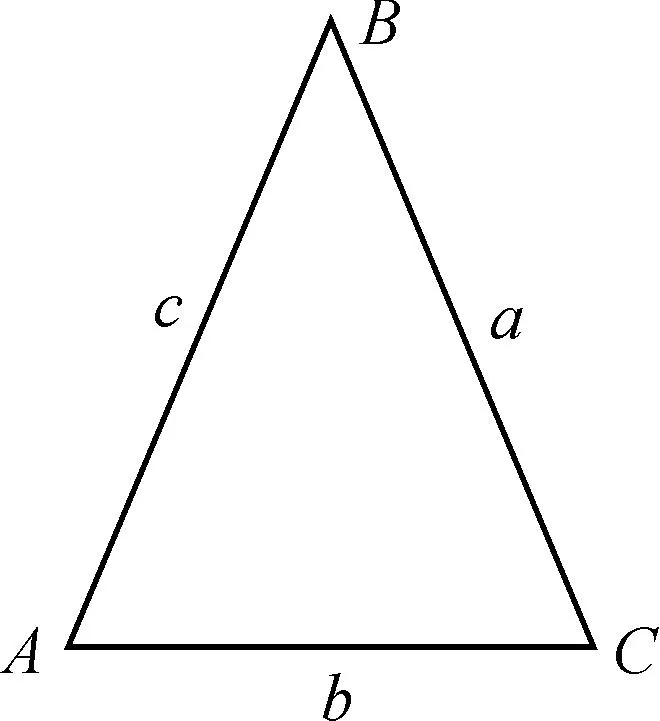
图7　三角形

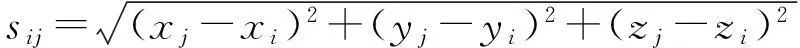
(2)

式中，(xi,yi,zi)、(xj,yj,zj)为两点的空间直角坐标。

7) 计算非整格网地表面积：非整格网区域如图8所示，计算地表面积方法就是将非整格网区域所有界址点构三角网[7-9]，计算三角网中三角形地表面积累计之和，即得到非整格网地表面积，如图9所示。

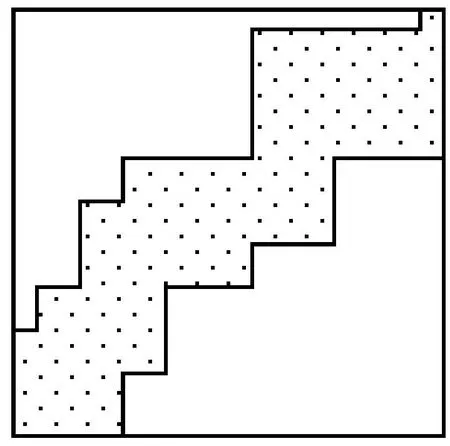
图8　非整格网区域

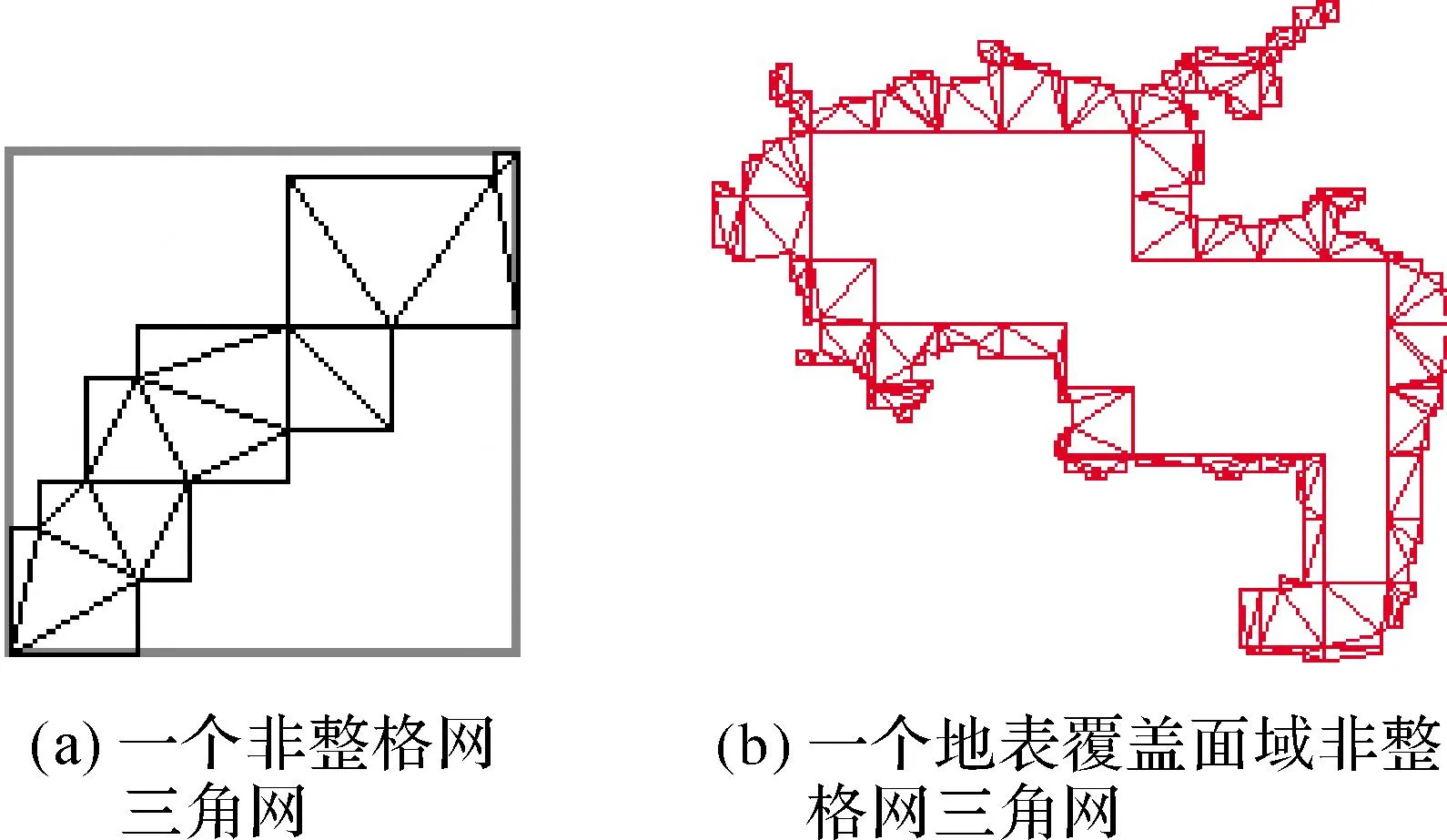
图9　三角网

四、试验及结果分析

笔者的研究以陕西省吴堡县地理国情监测成果的地表覆盖和DEM数据为基础，进行了地表面积计算与分析。在本文中，以其中两个比较复杂且具有代表性的地表覆盖面域为例，计算其地表面积，并进行详细的分析，面域如图10所示。

1) 将1∶10 000分辨率为5 m的DEM数据内插为4 m、3 m、2 m分辨率数据。使用DEM正常高和似大地水准面模型恢复地形表面的三维空间几何模型，计算图10地表面积，结果见表1。

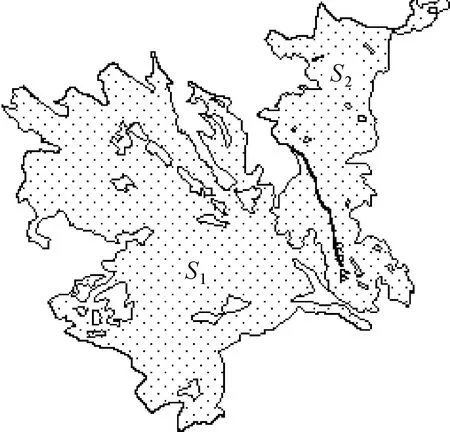
图10　地表覆盖面域

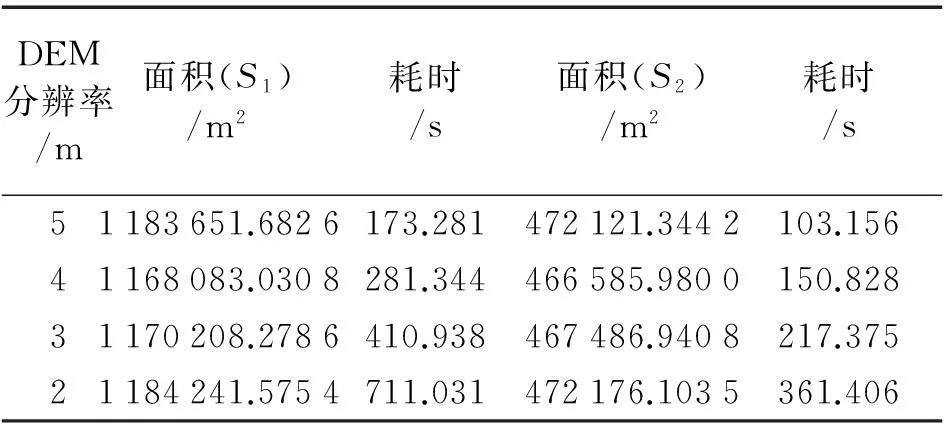
DEM分辨率/m面积(S1)/m2耗时/s面积(S2)/m2耗时/s51183651.6826173.281472121.3442103.15641168083.0308281.344466585.9800150.82831170208.2786410.938467486.9408217.37521184241.5754711.031472176.1035361.406

从表1可以看到，DEM分辨率不同，计算的地表面积值及效率也不同，分辨率越高，计算效率越低。分辨率2 m数据计算的地表面积与分辨率5 m数据计算的地表面积值相差比较小，前者计算效率比后者慢3～4倍。综合计算精度与效率，建议使用5 m分辨率DEM。

2) 使用1∶10 000分辨率为5 m的DEM数据正常高和似大地水准面模型恢复地形表面的三维空间几何模型，计算961个地表覆盖面域的地表面积，见表2中采用大地高计算地表面积。

3) 使用1∶10 000分辨率为5 m的DEM数据正常高，忽略似大地水准面模型，计算961个地表覆盖面域的地表面积，见表2中采用正常高计算地表面积。

表2　地表覆盖面域地表面积　m2

从表2可以看到，似大地水准面模型对计算地表面积影响非常小，在实际计算地表面积时，对似大地水准面比较平缓的地区，可以不考虑似大地水准面模型对地表面积计算的影响。

4) DEM正常高高程对地表面积计算影响。一个整格网，4个点正常高相同，假设将其中一个格网点的正常高逐步抬高0.5 m，用似大地水准面模型恢复地形表面的三维空间几何模型，计算其整格网地表面积，计算结果见表3。

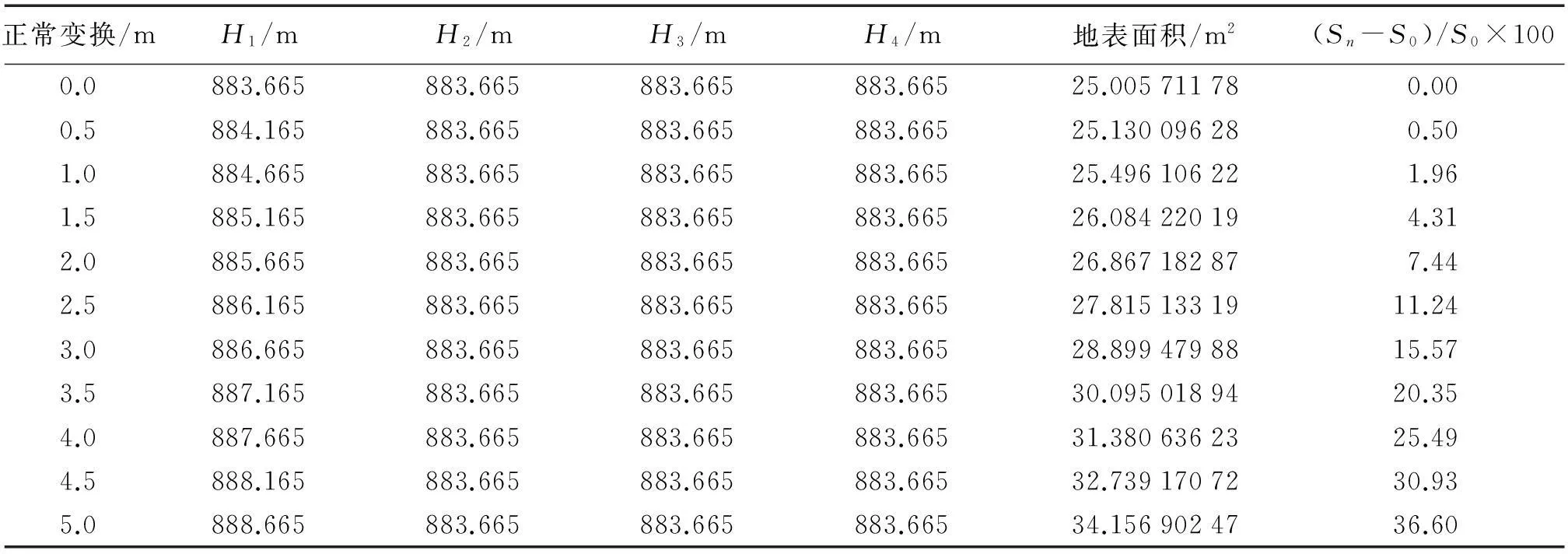
表3　正常高变化对计算地表面积影响

从表3可以看到，正常高对计算地表面积影响比较大，也进一步证明表1 DEM分辨率不同，计算的地表面积值也不同。建议在实际计算时， 用1∶10 000分

辨率为5 m的DEM成果计算地表面积。

五、结束语

本文从地表面积的定义、三维空间恢复方法、面状要素地表面积计算思路到计算的具体实现、计算结果分析等进行了较为全面的阐述，从实际计算结果分析了计算的效率和精度，并对计算中的DEM分辨率、高程、高程异常等因素的影响进行了分析和比较。经过实际验证，文中提出的计算方案高效可行，可对地理国情监测中的地表面积计算与统计提供有价值的参考。

参考文献：

[1]魏东,张秀程.基础递归算法的三维地形面积计算方法研究[J].工程地质计算机应用，2007(3):5-7.

[2]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉：武汉大学出版社,2009.

[3]吴秀琴,张洪岩,李瑞改,等.ArcGIS 9地理信息系统应用与实践[M].北京:清华大学出版,2008:231-233.

[4]樊建华,黄有群,刘嘉敏.带空洞的多边形求交集算法[J].沈阳工业大学学报,2001,23(5):429-431.

[5]杨维芳.两个复杂多边形求交的矢量算法[J].兰州铁道学院学报：自然科学版,2002,21(1):108-110.

[6]四川矿业学院数学教研组.数学手册[M].北京：科学出版社,1978.

[7]武晓波,王世新,肖生春.Delaunay三角网的生成算法研究[J].测绘学报,1999,28(1):28-34.

[8]张渭军.改进Delaunay生长算法研究[J].测绘科学,2011,36(4):58-59.

[9]余代俊，蒲朝旭，朱逍贤.一种Delaunay三角剖分的改进算法[J].测绘通报,2014(6):51-54.

[10]薛树强, 党亚民, 秘金钟,等. 顾及非线性地形因子的地表面积计算[J]. 测绘学报， 2015, 44(3): 330-337.