GPS高程拟合方法研究及精度对比试验

张　潘,余代俊,张玉刚,许　馨

(1. 成都理工大学现代测量技术及应用研究所，四川 成都 610059； 2. 西藏自治区

测绘院，西藏 拉萨 850000)

ZHANG Pan,YU Daijun,ZHANG Yugang,XU Xin

GPS高程拟合方法研究及精度对比试验

张潘1,2,余代俊1,张玉刚2,许馨2

(1. 成都理工大学现代测量技术及应用研究所，四川 成都 610059； 2. 西藏自治区

测绘院，西藏 拉萨 850000)

Research on GPS Elevation Fitting Method and Accuracy Comparison Experiment

ZHANG Pan,YU Daijun,ZHANG Yugang,XU Xin

摘要：利用GPS高程拟合技术求得满足一定精度的正常高是测绘研究的重要问题之一。本文通过某试验区GPS控制网数据成果，采用加权平均法、二次曲面拟合法求取高程异常值，并将最终成果与三等水准测量成果进行了对比分析得出，当已知点呈区域面分布时，二次曲面拟合法拟合精度优于加权平均拟合法，且拟合精度达毫米级，证明了该模型在实际运用中的优越性。

引文格式： 张潘,余代俊,张玉刚,等. GPS高程拟合方法研究及精度对比试验[J].测绘通报，2015(9)：54-56.DOI:10.13474/j.cnki.11-2246.2015.0278

关键词：高程拟合；加权平均法；二次曲面拟合；高程异常

中图分类号：P228.4

文献标识码：B

文章编号：0494-0911(2015)09-0054-03

收稿日期：2014-07-30

作者简介：张潘(1987—)，男，硕士，助理工程师，研究方向为摄影测量与遥感。E-mail:980506099@163.com

一、引言

GPS测量可以获得高精度的三维坐标，它的平面相对定位精度已经十分精确，但是它得到的高精度的大地高与我国采用的正常高系统不一致，只具有几何意义，如何将大地高转换为正常高，在一定程度上代替传统的水准测量作业，是测绘行业研究的热点。

我国采用正常高系统，大地高起算面为参考椭球面，正高起算面为大地水准面，正常高系统起算面为似大地水准面。三者关系如图1所示。

图1　大地高、正高和正常高关系

(1)

二、GPS拟合模型

1. 加权平均法

加权平均法，是由内插点周围部分已知点的高程异常加权平均求得该点的高程异常。设在内插点周围选n个已知点，高程异常为ξi(i=1，2，…，n)，对应的权为Pi，则内插点j的高程异常为

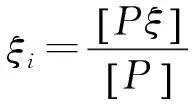
权Pi可根据已知点至内插点的距离来计算

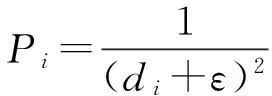
式中，di为已知点i至内插点j的水平距离；ε为一小正数，以防止权函数的分母趋于0，通常ε取0.01，单位与di单位相同。

2. 二次曲面拟合

曲面拟合法是认为高程异常在一定范围内变化平缓的前提下，将高程异常(或高程异常差)近似地看作是一定范围内各点坐标的曲面函数。设测站点的高程异常与其平面坐标的函数关系式为

ξi=f(xi,yi)+vi

式中，f(xi,yi)为所选定的曲面函数，也即ξi的趋势值；vi为其残差。当选择多项式曲面拟合法时

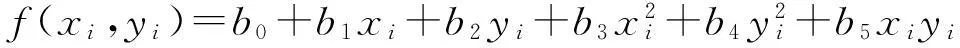
式中，bi(i=0，1，2，…，5)为待定系数；(xi，yi)为i点的平面坐标

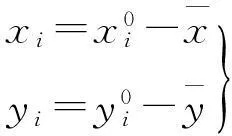
若有n个点，则可以得到下面的矩阵形式

ξ=XB+v

用最小二乘求出bi(i=0，1，2，…，5)6个待定参数，求出参数后根据拟合模型得出高程异常值ξi，并由式(1)得出正常高。

三、试验分析

1. 控制网概况

试验区结合GPS控制网及三等水准进行研究，控制网选取11个点作为已知点，按GPS D级网进行观测(如图2所示)，观测仪器采用Trimble R8静态接收机，观测时段数大于1.6，每时段时长大于60 min，测量开始与结束时各量取3次仪器高，仪器高前后不超过5 mm。

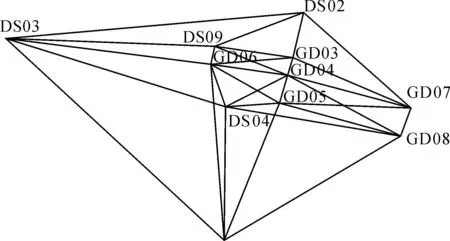
图2　GPS观测网

2. 高程拟合试验

此次试验采用加权平均法及二次曲面拟合，其中加权平均法选取方案1为6点(DS05、DS03、DS02、GD07、GD08、GD06)、方案2为7点(DS05、DS03、DS02、GD07、GD08、GD06、GD05)、方案3为6点(DS05、DS03、GD07、GD08、GD06、GD05)，其余点作为检查点，拟合结果见表1。

二次曲面拟合选取方案1为6点(DS05、DS03、DS02、GD07、GD08、GD06)、方案2为6点(DS05、DS03、GD07、GD08、GD06、GD05)，其余点作为检查点，拟合结果见表2。

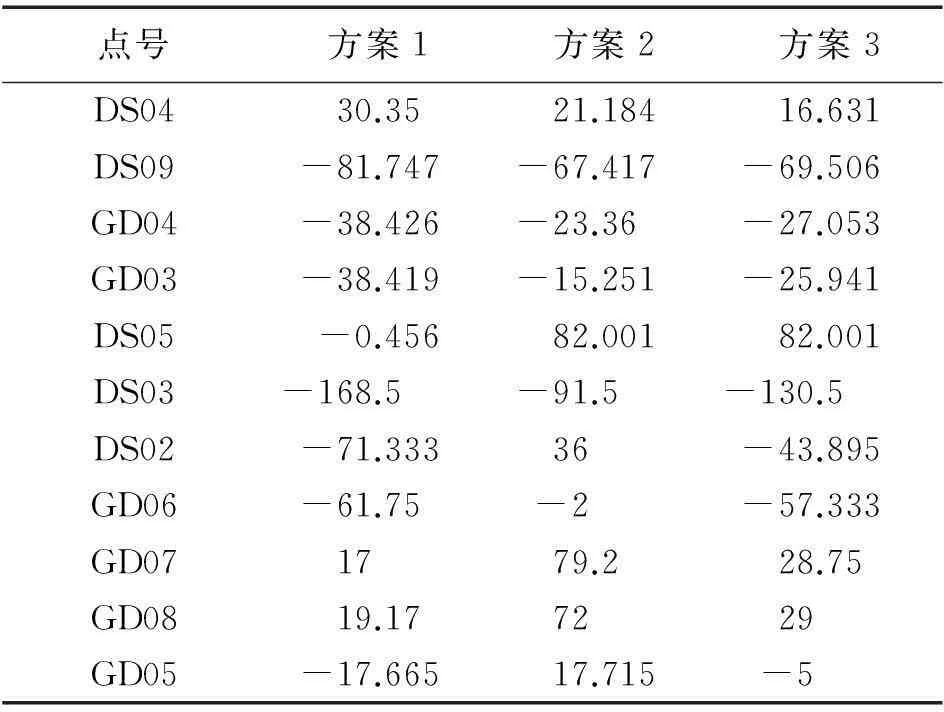
表1　加权平均法检查点残差　mm

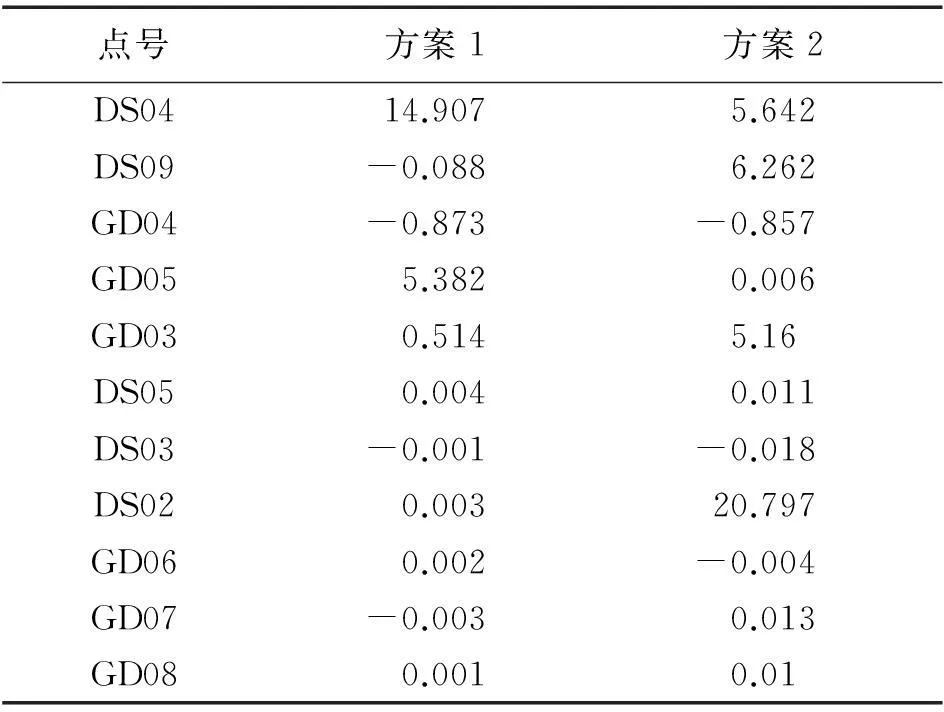
表2　曲面拟合法检查点残差　mm

3. GPS水准精度评定

(1) 内符合精度

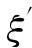
式中，n为参与拟合计算的已知GPS水准联测点数。

(2) 外符合精度

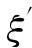
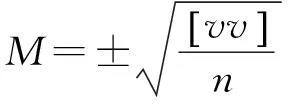
式中，n为参与检核的GPS水准联测点数。

根据表1、表2计算试验区的内符合精度及外符合精度，计算结果见表3。

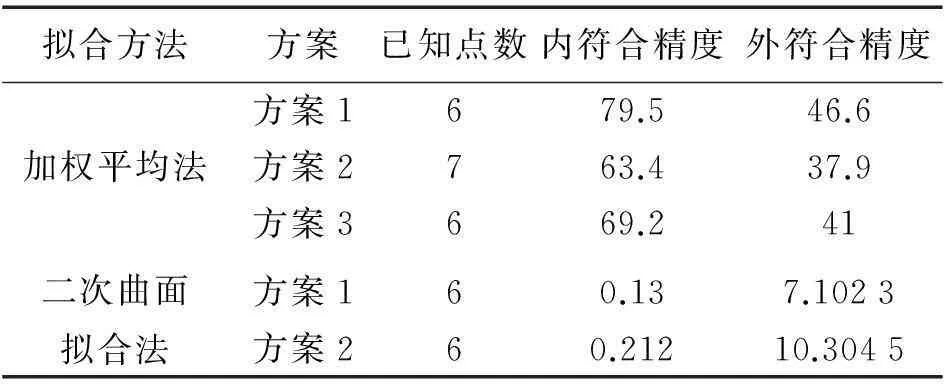
表3　两种模型精度对比　mm

四、结论

1) 当测区已知点呈面状分布时，加权平均法内符合精度与外符合精度都远大于二次曲面拟合的符合精度，并通过与三等水准成果的对比，得出二次曲面拟合精度优于加权平均法。

2) 二次曲面拟合适用于地形较复杂地区的高程拟合，拟合时已知点数量不少于6个，同时在拟合时已知点点位分布对拟合精度影响较大。当已知点包含整个测区时，拟合精度较稳定；当待定点在已知点覆盖范围之外时，拟合精度较低。

3) GPS高程拟合精度取决于地形起伏变化均匀程度，用数学模型求解某一点高程异常时，存在一定的误差，因此选择某种模型进行高程拟合时，可根据测区实际情况选择拟合模型。

参考文献：

[1]吉渊明, 赵水泉. 曲面拟合法求GPS网正常高的几点认识[J]. 测绘通报, 1998(7): 18-20.

[2]徐绍铨, 张华海, 杨志强, 等. GPS测量原理及应用[M]. 武汉: 武汉测绘科技大学出版社, 1998.

[3]刘基余. 全球定位系统原理及其应用[M]. 北京: 测绘出版社, 1993.

[4]王岩, 刘茂华, 党永超. 小地区GPS高程拟合的方法研究与实施[J]. 测绘通报, 2012(S0): 66-68.

[5]沈学标. GPS水准高程拟合精度的分析[J]. 测绘通报, 1998(7): 21-22.

[6]闫伟, 高俊强, 王维. 小地区GPS高程拟合和水准测量对比试验[J]. 南京工业大学学报, 2007, 29(5): 93-96.

[7]何美琳, 文鸿雁, 潘元进, 等. GPS高程拟合的方法比较[J]. 测绘科学, 2013, 38(3): 63-65.

[8]国家测绘局. GB/T 18314—2001 全球定位系统(GPS)测量规范[S]. 北京: 中国标准出版社, 2001.

[9]张兴福,刘成.综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J]. 测绘学报，2012， 41 (1): 25-32.