宽体混凝土斜拉桥主梁新构造研究
牟宗军,翟晓亮,冯云成(中交第一公路勘察设计研究院有限公司)
宽体混凝土斜拉桥主梁新构造研究
牟宗军,翟晓亮,冯云成
(中交第一公路勘察设计研究院有限公司)
摘要:本项目以五河口斜拉桥的设计实践为背景,详细研究了宽体混凝土斜拉桥主梁的受力特性,率先提出了带钢筋混凝土纵向加筋肋(疏肋)板的宽体混凝土斜拉桥主梁新构造。通过有限元仿真分析和理论分析研究了带纵向混凝土加筋肋的宽体混凝土斜拉桥主梁的受力机理和分析计算方法。研究结果表明:带钢筋混凝土纵向加筋肋的宽体混凝土斜拉桥主梁能够很好地解决混凝土斜拉桥主梁过宽导致传统双边箱梁、π型梁中间板过宽、配筋量大和刚度不足等问题,且能够有效降低主梁剪力滞后效应程度、提高截面利用率和提高桥面刚度,能够很好地适应宽体混凝土斜拉桥主梁的受力要求,是一种经济、合理、安全、耐用的新型主梁截面形式。
关键词:宽体斜拉桥;纵向加筋桥面板;双边箱主梁;剪力滞;空间有限元
中图分类号:U442
文献标识码:C
文章编号:1008-3383(2015) 04-0088-04
Research on new structural behaviour of wide main girder cable-stayed bridge
MOU Zong-jun,ZHAI Xiao-liang,FENG Yun-cheng
(CCCC First Highway Consultants Co.,LTD)
Abstract:A new structure of concrete main girder with reinforced concrete longitudinal stiffening ribs was provided for wide concrete girder of cable-stayed bridge,based on the design practice of five-river cable-stayed bridge.In order to study the mechanical behaviors of concrete main girder with reinforced concrete longitudinal stiffening ribs,numerical analysis and theoretical analysis were performed.The mechanical behaviour and calculation and analysis methods were obtained.Analysis results show that these aspects can be solved through concrete main girder with reinforced concrete longitudinal stiffening ribs.This structure can reduce the degree of the shear lag effect of main girder,increase cross section utilization ratio of section and rigidity of deck.It is also a economic,reasonable,safe and durable section form which also meet the requirement of the allowable force.
Key words:wide main girder cable-stayed bridge; lengthways stiffened bridge deck slab; double side box girders; shear lag; model test;analysis of 3D finite element
0 前言
随着国民经济不断发展,交通量逐年增加,桥梁车道数不断增加,桥梁的宽度不断增加,尤其是市政桥梁,36 m以上宽度的桥梁越来越多。桥梁宽度增加到一定程度后,以前原有的二维平面设计方法逐渐暴露出一些不足,桥面板的纵向的剪力滞后问题和横向受力变得尤为突出。混凝土斜拉桥主梁过宽导致传统的双边箱梁构造、π型梁中间板过宽,配筋量大、刚度不足等问题突出,急需针对这一问题提出更为合理的构造措施。
依托五河口斜拉桥的设计工作实践,提出带混凝土加筋肋肋的宽体混凝土斜拉桥主梁新构造,即在宽体双边箱混凝土主梁的桥面板下增设纵向加筋肋。增设纵向混凝土加筋肋的宽体混凝土斜拉桥主梁可以减小斜拉桥主梁悬臂施工时的桥面板混凝土正应力及剪力滞系数,并且增强桥面板的抗弯刚度,这使宽体双边箱混凝土主梁节段悬臂施工过程中降低了桥面板混凝土受力开裂的风险。重点对纵向混凝土加筋肋对主梁设置后桥面剪力滞效应的影响和纵向受力状态的影响。
1 工程背景
1.1工程概况
五河口预应力混凝土斜拉桥(以下简称“五河口斜拉桥”)位于宿淮高速公路、宁淮高速公路及淮安西环的共线段上,是一座双塔双索面预应力混凝土斜拉桥。该桥主梁跨径组成为152 m +370 m +152 m,总体布置见图1。
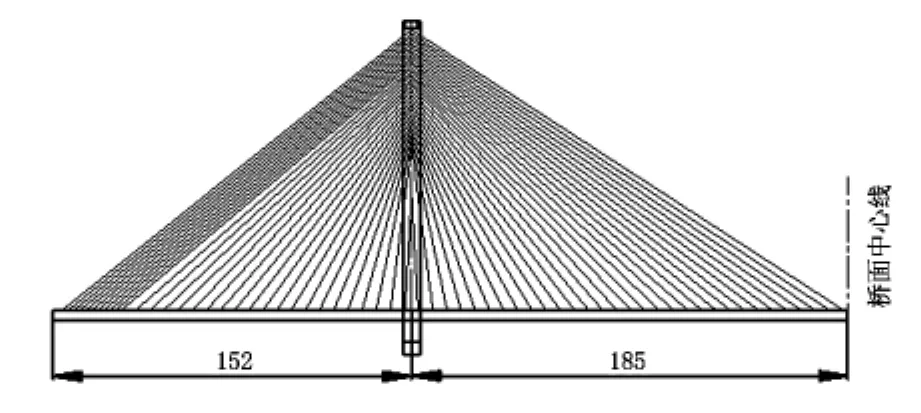
图1 主桥总体布置(单位: m)
主梁采用双边箱断面,主梁中心高3.2 m,宽38.6 m,桥面板厚0.3 m,桥面设2%的双向横坡。风嘴部分宽为0.5 m。全桥共划分了123个梁段,分索塔区梁段、标准梁段、无索区梁段、边跨密索区梁段和中、边跨合拢段。塔区梁段共4个,梁段长10.0 m,标准梁段共94个,梁段长6.0 m,边跨密索区梁段共20个,梁段长2.5 m,中、边跨合拢段3个,长度均为2.0 m。主梁断面见图2。
索塔成H形,预应力钢筋混凝土结构,索塔高137.1 m,上塔柱高77.0 m,中塔柱高47.0 m。顺桥向上塔柱宽7.0 m,中塔柱从上横梁底部7.0 m宽变化到下横梁中心处的8.0 m宽并以此斜率延伸到承台,倾斜率94∶1。
斜拉索采用OVM250系列环氧涂层钢绞线拉索及相应的锚具,标准强度为1 860 MPa,弹性模量为1. 95×105MPa。斜拉索一端为张拉端锚具,另一端为锚固端锚具。斜拉索在主梁上的标准索距为6 m,边跨B20-B30索的索距为2.5 m。斜拉索在索塔上的标准索距为1.5 m和2 m。
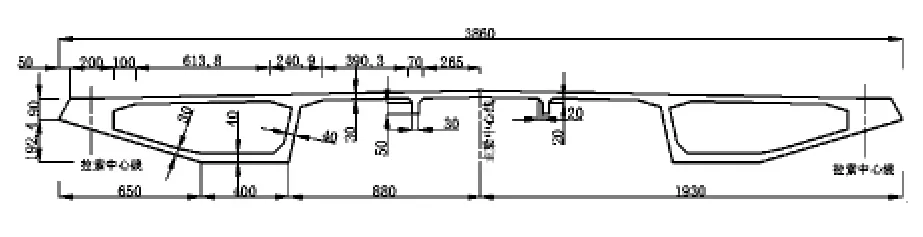
图2 主梁横断面(单位: cm)
1.2主要技术标准
(1)建设标准:双向六车道高速公路。
(2)设计基准期: 100年。
(3)计算行车速度: 120 km/h。
(4) 0.5 m(风嘴) +1.3 m(拉索锚固区) +0.5 m(防撞护栏) +15.5 m(行车道) + 3.0 m(中央分隔带) + 15.5 m(行车道) + 0.5 m(防撞护栏) + 1.3 m(拉索锚固区) + 0.5 m(风嘴) =38.6 m。
(5)地震动峰加速度:地震基本烈度为Ⅶ度,按Ⅷ度设防。
2 主梁剪力滞效应
剪力滞系数在斜拉桥中是指考虑剪力滞效应的纵向正应力(弯曲与轴力共同引起的)与按初等梁理论计算的纵向正应力之比值。斜拉桥在施工过程中主梁截面的内力在某些工况下大于成桥状态的内力,使得施工内力控制截面设计。选取最大双悬臂、最大单悬臂、成桥阶段三个有代表性的典型工况作为分析对象,来分析主梁截面剪力滞效应特点。
为了解主梁纵向正应力沿纵向全长的分布规律,取出了横截面顶板的几个关键节点沿纵向全长的纵向正应力计算结果。为了叙述的方便,将主梁横截面上关键部位的点分别用大写的英文字母作标记,如图3所示,A~G点距横向对称线的距离分别为18.8 m,17.4 m,12.761 m,8.403 m,6.323 m,3.0 m,0.0 m;各点的横向位置如图3所示。

图3 主梁横截面各点示意图
2.1最大双悬臂阶段的剪力滞分析
采用ANSYS空间有限元软件建立本桥最大双悬臂施工阶段空间分析模型,如图4所示。
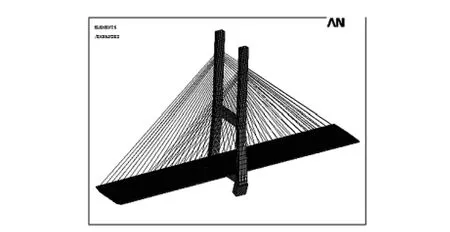
图4 最大双悬臂阶段空间分析模型
通过计算发现最大双悬臂阶段主梁顶板纵向正应力分布很不均匀,但是很多梁段内的主梁纵向正应力分布规律相似。最大双悬臂阶段主梁顶板剪力滞系数除去悬臂端部与根部几个梁段外,其他梁段均呈现相似的分布规律。悬臂端部的正应力分布无明显规律是由于挂篮荷载和预应力荷载的作用,这些集中荷载作用点处产生了较大的应力集中从而改变了顶板的应力分布规律。根部截面正应力分布规律不明显的原因是由于主梁采用了与其他梁段不一样的闭口箱形断面造成了顶板应力分布的改变。
在顶板各关键点的剪力滞纵向分布中,以横截面的边点(A点)与横截面中点(G)点变化最为剧烈。A点在各横梁设置截面处均出现了向下的突变,剪力滞系数一般在0.5左右,最小的为0.25;而G点正好相反,在各横梁设置截面处均出现了向上的突变,剪力滞系数一般在1.2左右,最小的为1.62。
设计者关心的是平面应力最大点的剪力滞系数,还有空间应力最大点处对应的剪力滞系数。因此,有必要把各截面上空间应力最大点找出来。而据上述分析,各截面上应力最大点是不一样的,点A、F、G都有可能,但对于每个梁段内,应力最大值总是出现在横梁对应截面顶板上的G点,而应力最小值出现在横梁对应截面顶板上的A点。
将A、G点的空间应力与G点平面应力曲线一起画在图5中,这样可以知道空间最大应力值在中跨悬臂27 m处,应力值为7.24 MPa,对应的平面应力值为6 MPa,λ=1.207,而平面最大应力值在中跨悬臂22 m处,应力值为6.71 MPa,对应的空间应力值为6.33 MPa,λ=0.943。
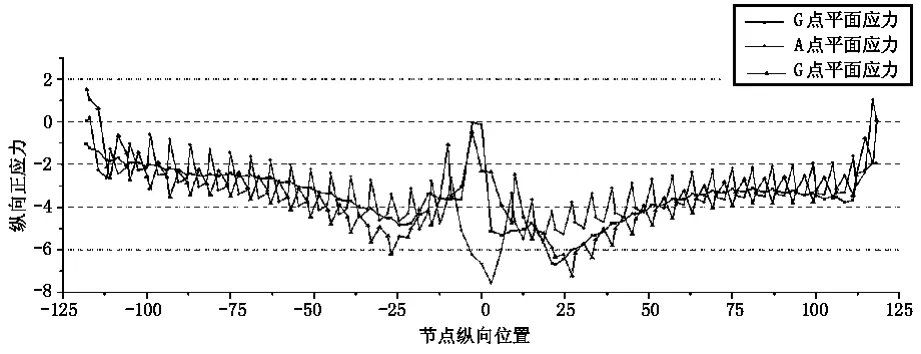
图5 最大双悬臂阶段空间与平面最大应力对比(单位: MPa)
2.2最大单悬臂阶段的剪力滞分析
在最大单悬臂阶段,由于边跨已经合拢,受到边跨支承条件变化的影响,边跨主梁的剪力滞效应比最大双悬臂阶段减小了。由于边跨现浇段采用的是单箱三室断面,而且梁上作用有压重,所以其剪力滞效应与悬臂浇筑的梁段不一样。而1~19#这些悬臂浇筑的梁段的剪力滞系数纵向分布规律与最大双悬臂阶段相比没有多大变化,只是数值上有所减小。这说明边跨合拢后,边跨主梁上后期施加的荷载对已浇梁段的剪力滞效应起减小作用,但没有改变其分布规律。
从图6可看出,边跨剪力滞效应最大的发生在19#块横
梁处截面,λ=1.56。最小的剪力滞效应在边跨支承处附近,λ=0,其他梁段大都在0.5~1.5之间。值得注意的是,边跨现浇段的剪力滞效应复杂,剪力滞系数变化幅度剧烈,其应力最大值出现在索张拉点附近而不是平面分析中的横截面中点。对于1~19#梁段来说,每个梁段的最大应力值都出现横梁所在截面的截面中点处。
与边跨相比,中跨的边界条件没有发生变化,而是继续悬臂浇筑到30#梁段,所以中跨梁段的剪力滞系数纵向分布的规律没有发生改变。
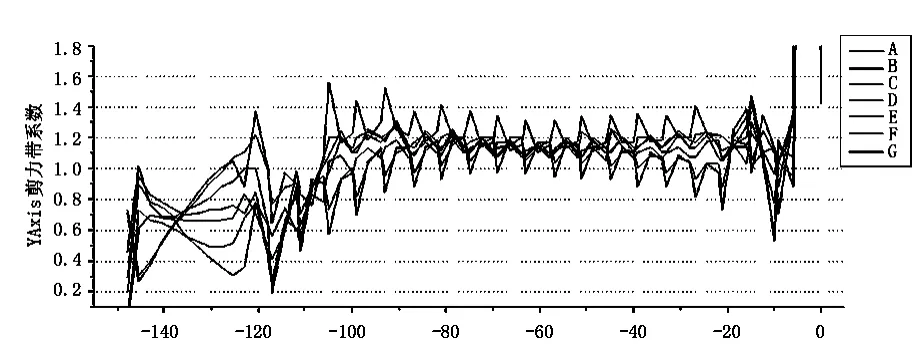
图6 边跨剪力滞系数沿纵向分布
从图7可看出,除去根部梁段与悬臂端,中跨剪力滞效应最大的发生在25#梁段横梁处截面,λ= 1.31。最小的剪力滞效应在3#梁段,λ=0.58,其他梁段大都在0.6~1.3之间。对于3~28#梁段来说,每个梁段的最大应力值都出现横梁所在截面的截面中点处。而悬臂端的29、30#梁的应力最大值则出现在索张拉点附近。
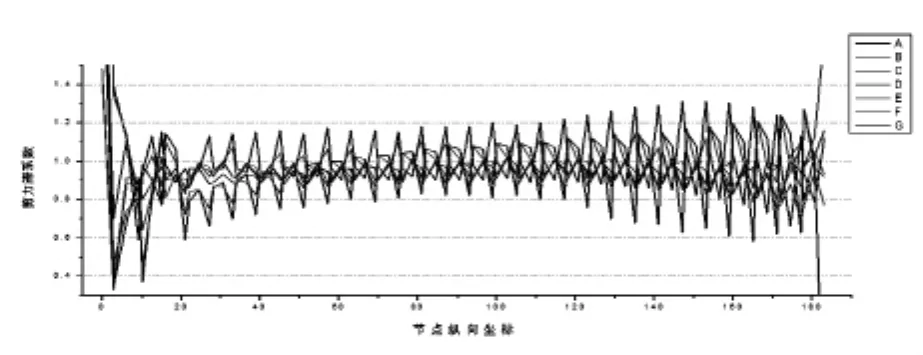
图7 中跨剪力滞系数沿纵向分布
根据A、G点的空间应力与G点平面应力的比较可知道,最大单悬臂阶段空间最大应力值在边跨悬臂27 m处,应力值为11.01 MPa,对应的平面应力值为7.79 MPa,λ= 1.41,而平面最大应力值在中跨悬臂22 m处,应力值为9.165 MPa,对应的空间应力值为8.4 MPa,λ=0.917。

图8 最大单悬臂阶段空间与平面最大应力对比(单位: MPa)
2.3成桥阶段的剪力滞分析
在成桥阶段,由于中跨的合拢,中跨梁段的边界条件也发生了改变,而且悬臂端挂篮荷载、配重荷载的拆除,全桥二期恒载的施加等因素都使得成桥阶段主梁的剪力滞效应与最大单悬臂阶段相比发生了较大的改变。
在成桥阶段,主梁的剪力滞系数的数值和变化幅度比最大单悬臂阶段减小。对于边跨而言,现浇段的剪力滞分布规律与最大单悬臂阶段近似,只是在边跨支承处附近的剪力滞效应增大许多,这是因为成桥后尾索的索力增大造成的。而边跨3~19#梁段的剪力滞效应与最大单悬臂阶段相比,均有所减小,剪力滞效应最大的发生在19#块横梁处截面,λ= 1.38。最小的剪力滞效应在边跨支承处附近,λ=0.65,其他梁段大都在0.6~1.4之间。横截面上各点的剪力滞系数差值也减小了许多,这说明截面上的应力分布趋于均匀。0#块附近区域由于塔梁固结的解除和0#索的张拉,空间与平面分析结果的差异减小了很多,剪力滞系数也随之减小。
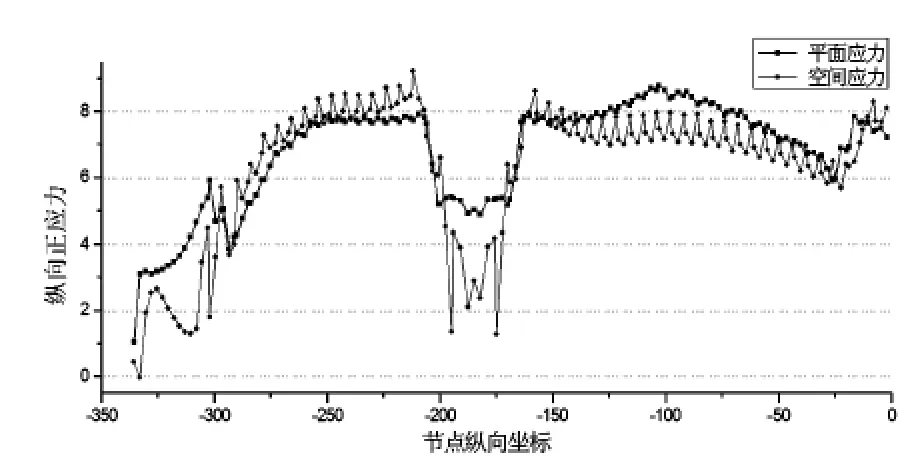
图9 成桥阶段顶板中点G空间与平面正应力比较(单位: MPa)
从剪力滞系数数值上看,边跨最大剪力滞系数为1.4,中跨为1.1。但从图9、图10可看出,剪力滞系数较大的区域,对应的应力值都比较小,所以剪力滞效应的影响并没有使主梁的最大应力值有明显的增大。但是,由于横向受力的不均匀性,横截面上各点的剪力滞系数相差较大,同一截面上同时出现了正负剪力滞现象,这是通过平面分析无法得到的结果。
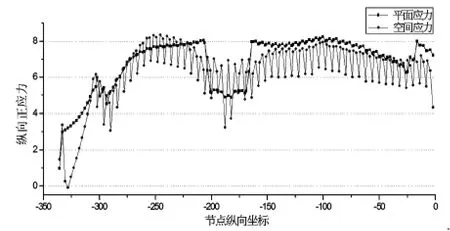
图10 成桥阶段顶板边点A空间与平面正应力比较(单位: MPa)
2.4混凝土加筋肋对剪力滞效应的影响
五河口斜拉桥主梁设计过程中为了改善主梁桥面板受力,在混凝土桥面板上增设了两道混凝土加筋肋,为了得到混凝土加筋肋对剪力滞效应的影响,这里以下三种工况进行了对比: (1)不设混凝土加筋肋; (2)设混凝土加筋肋,刚度为EI; (3)设混凝土加筋肋,刚度为2EI。
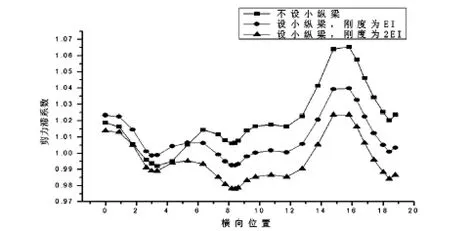
图11 L/4截面剪力滞系数横向分布
三种工况下计算结果见图11和12,图中纵坐标为个点剪力滞后系数,横坐标为各点相对于主梁中心线的距离。从
图11和12中可以看出主梁增设混凝土加筋肋后,剪力滞后系数总体上有所下降且随着混凝土加筋肋刚度的增大,剪力滞后系数进一步下降;但是对于不同横断面位置、同一横断面不同计算点处剪力滞后系数下降程度均有所不同。设置混凝土加筋肋后,主梁的剪力滞效应有所降低,但降低幅度不大。以L/2截面为例,增设混凝土加筋肋后,剪力滞系数最多减小4.9%,如增设2EI的混凝土加筋肋,剪力滞系数最多减小6.5%。对于剪力滞系数沿纵向分布的影响,增设混凝土加筋肋后,对减小剪力滞效应有一定的作用,而且在剪力滞系数越大的区域,这种减小作用越明显。
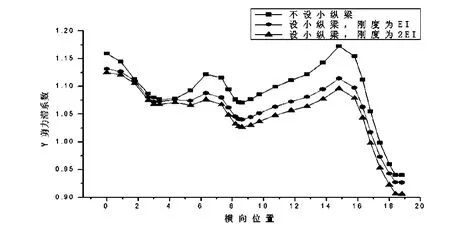
图12 L/2截面剪力滞系数横向分布
3 轮载作用下带混凝土加筋肋主梁的正应力
从宽体斜拉桥双边箱混凝土主梁构造上讲,不增设纵向加筋肋的双边箱之间桥面板是弹性支撑在两对边横隔板及两边箱梁内腹板之间的一块整体板,但增设纵向加筋肋后双边箱之间桥面板,除了与不设纵向加筋肋的桥面板有相同的四周边支撑条件外,两边箱之间的桥面板还支撑在纵向加筋肋之上。
双边箱主梁的桥面板除了作为主梁截面整体承受截面上的作用效应外,车辆轮载直接作用在桥面板上,其作用效应对混凝土桥面板的钢筋配置有重要影响。对图13a所示的双边箱间桥面板,其远远大于,实际上轮载作用下,受力是单向板状况。但是,增设了纵向加筋肋后(图13b),这时双边箱之间的桥面板类似于四边弹性嵌固的连续板。
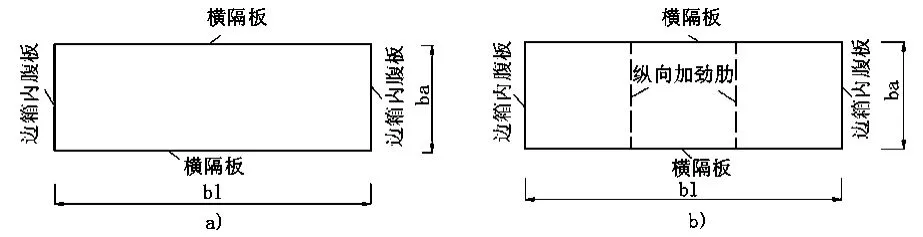
图13 双边箱间纵向加劲桥面板平面示意图注:图中bl为双边箱之间桥面板的宽度; ba为箱梁节段的横隔板之间的宽度。
(1)有限元模型。
主梁节段用空间实体单元SOLID 45来模拟,弹性模量E =3. 65×104MPa,容重γ=26 kN/m3,泊松比为0.166 7;斜拉索用杆单元LINK8来模拟,拉索的两端采用全约束,主梁节段两端加强迫位移,该位移大小由MIDAS/Civil中整体杆系模型计算得出。
(2)轮载作用在两个横梁之间。
当轮载作用在两个横梁之间(见图14中),截面1和截面2上各计算点的板顶面正应变见图15和图16。
从图15和图16可以看出不管是否设置混凝土纵向加筋肋,在横隔板处桥面板观测的计算点始终是拉应变,而横隔板之间桥面板观测的计算点都是压应变,曲线的整体趋势并没有改变;混凝土纵向加筋肋的设置对纵向受力是有利的。其中,截面2在设置混凝土纵向加筋肋后,最大压应变减小了63%,最大拉应变减小了96%;由于截面2靠近混凝土纵向加筋肋,2#截面的纵向受力性能影响程度要大于对1#截面纵向受力的影响。
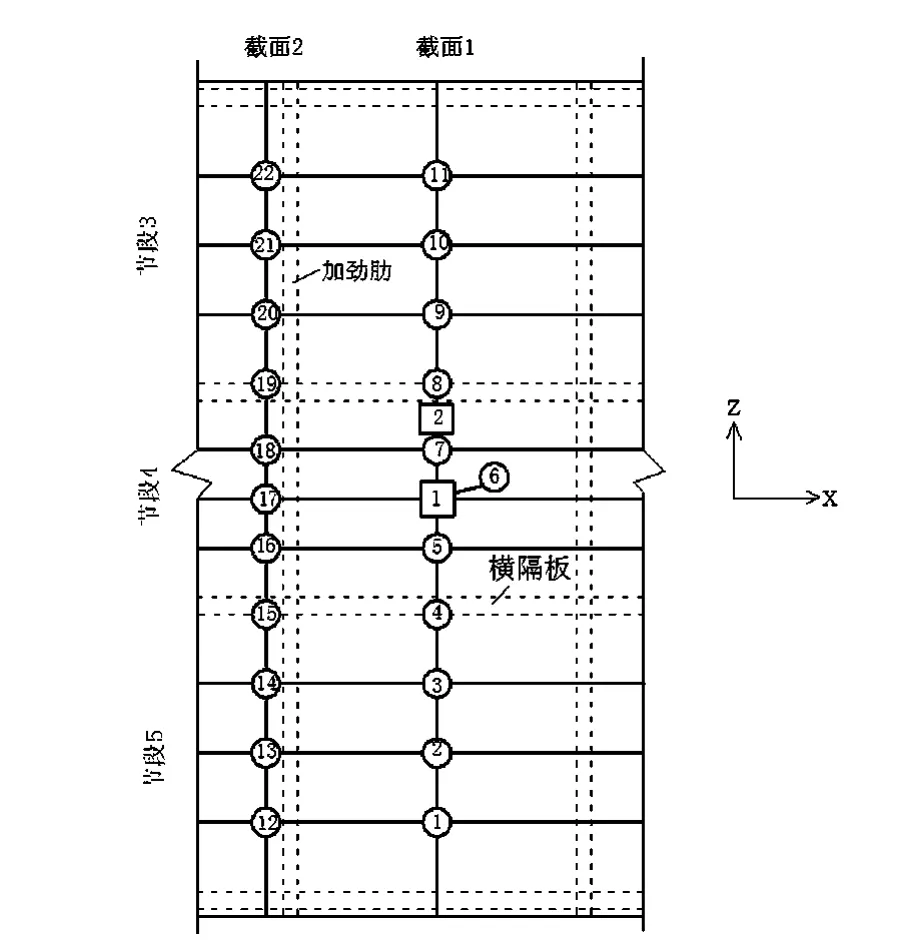
图14 计算点布置

图15 截面1的正应变值比较(单位:10-9ε)
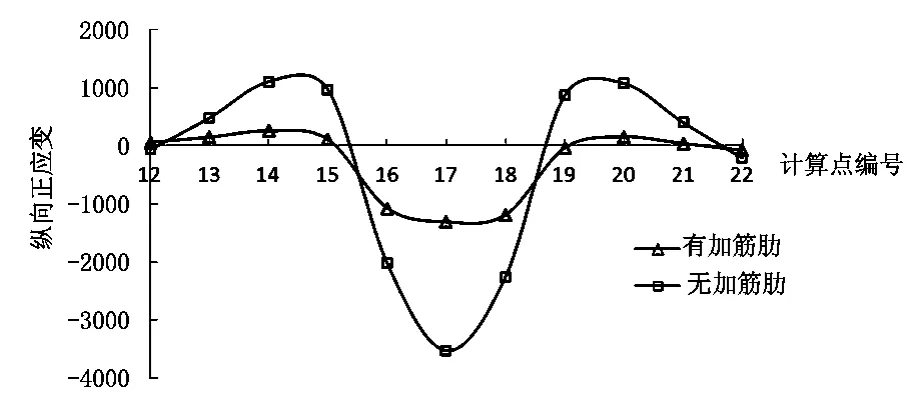
图16 截面2的正应变值比较(单位:10-9ε)
(3)轮载作用在靠近横梁位置。
当轮载作用在靠近横梁位置时(见图14中),截面1和截面2上各计算点的板顶面正应变见图17和图18。
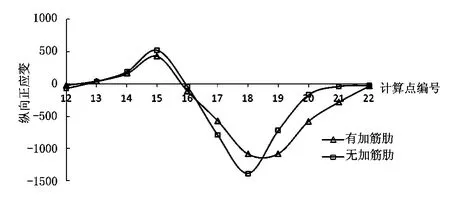
图17 截面2的正应变值比较(单位:10-9ε)
从图18和图19可以看出靠近纵向加筋肋的2#截面
偏载效应很明显,致使位于横隔板处的19#计算点受压应变,曲线的总体趋势没有大的改变。设置加筋肋后,7#计算点最大压应变减小了22%,4#计算点的最大拉应变减小了18%; 1#截面离纵向加筋肋稍远,偏载效应没有那么明显,曲线的整体趋势也没有改变,7#计算点的压应变比原来减小了19%。

图18 截面1的正应变值比较(单位:10-9ε)
4 结论
(1)宽体混凝土斜拉桥采用带混凝土纵向加筋肋主梁新构造后对减小双边箱主梁靠近悬臂端梁段的剪力滞效应有明显作用,但对其他梁段作用不明显。横梁的设置,会使得主梁应力分布更均匀,改善了主梁的受力,有效地减小了主梁的剪力滞效应,但进一步加强横梁则没有明显效果。
(2)宽体混凝土斜拉桥主梁设置纵向混凝土加筋肋后的边箱间桥面板,无论是轮载作用在跨中还是轮载作用在靠近横隔板时,都可以减小桥面板在跨中的纵向正应变和横隔板处的拉应变,但并没有改变其纵向受力的总体分布。
(3)宽体混凝土斜拉桥主梁桥面板上设置纵向混凝土加筋肋对主梁的整理受力影响不大,但是对局部受力的改善效果显著。
(4)带混凝土纵向加筋肋的宽体混凝土斜拉桥主梁能够有效解决混凝土斜拉桥主梁过宽导致传统双边箱梁、π型梁中间板过宽引起的结构受力缺陷,可以在同类型桥梁中推广使用。
参考文献:
[1]翟晓亮,王春生,冯云成,等.组合梁斜拉桥有效宽度系数及实用计算方法[J].长安大学学报(自然科学版),2013,33 (1) : 51-58.
[2]牟宗军,翟晓亮,冯云成.厦漳跨海大桥南汊主桥主梁设计与研究[J].桥梁建设,2013,43(4) : 26-32.
[3]万臻.斜拉桥常用截面形式主梁的剪力滞效应研究[D].西南交通大学,2002.
[4]许崇发.斜拉桥混凝土主梁桥面板模型试验与分析[D].东南大学,2004.
收稿日期:2014-11-12

