浅谈初中数学教学中学生逆向思维能力的培养

杨　昭　李文铭　（陕西师范大学数学与信息科学学院　710062）

浅谈初中数学教学中学生逆向思维能力的培养

杨昭李文铭（陕西师范大学数学与信息科学学院710062）

摘要：逆向思维是一种创造性的思维方式。数学作为一门较抽象的学科，在培养学生的逆向思维能力方面有着十分重要的作用。本文通过介绍在教学中加强学生对数学概念、公式、定理的逆运用及对逆向思维解题技巧的掌握，并结合分析法和反证法，探讨教师如何在初中数学教学中训练学生的逆向思维能力。

关键词：逆向思维初中数学培养

DOI：

10.16657/j.cnki.issn1673-9132.2016.01.155

正向思维一般是指传统的、逻辑的、习惯的思维方向，它在我们的生活和学习中经常采用。而逆向思维则是一种反向思维，它要求人们要善于从事物的正、反两个方向去思考问题，把一些原来一直如此的事物颠倒过来思考，从而认识事物的相反方面，揭示不同的现象，获得不同的效果，进而从中发现新的原理、新的方法、新的结构、新的思路。逆向思维在创新活动的过程中发挥着重要的作用，运用逆向思维去思考和处理问题，实际上就是以“出奇”去达到“制胜”。

在初中数学中存在许多互逆运算，如：加减、乘除、乘方与开方等。它们都是相辅相成的。要真正学好数学，灵活解决数学问题，正向思维和逆向思维都不可或缺。然而初中生由于受到思维定势的影响，在解决数学问题时普遍习惯于从问题的正面入手。长此以往，便会造成学生的解题思路狭窄、思维僵化，不利于学生今后的数学思维发展。

作为初中数学教师在教学中要有意识地加强逆向思维的训练，打破学生的思维定势。从基本的初中数学教材入手，寻找其中能够用于培养学生逆向思维的素材，并重视对其在课堂中的讲解，使这些材料充分发挥培养学生逆向思维的作用。同时，教师应鼓励学生积极思考，使学生在自主探究中发现数学学习的乐趣，这样既锻炼了学生的思维灵活性，又激发了学生学习数学的兴趣。

一、加强学生对数学概念的逆运用

数学概念的学习对学生来说理解难度较大。如果教师在教学之初，仅注重对概念的一个方面进行教学，学生在今后的应用中也会只单一的重视从这一方面进行思考。学生没有完整掌握概念的内容，就容易导致理解的偏差，从而影响数学学习。这就要求教师在对于数学概念的教学中，注重从正反两方面进行教学，使学生同时理解概念的正、逆两种形式。

如学习“相反数”概念时，教师可考虑从正面提出问题：相反数是什么？再从反方向提出问题：什么数的相反数是什么？同时，还可以设计如下互逆的问题：如果a=-8，那么-a=_____；如果-a=-8，那么a=_____。

又如，在教学“补角”概念时，教师就可这样引导学生从正、逆两方面来理解此概念：“如果α+β=180°，那么α和β互为补角”；反过来：“如果两个角α和β互为补角，那么α+β=180°”。

教师通过从正、逆两个角度巧设疑问，不仅训练了学生的逆向思维，同时使学生在学习数学概念之初就形成了完整的认识。

二、加强学生对数学公式、定理的逆运用

同数学概念的教学一样，教师在对数学公式、定理的教学中也应有意识地引导和培养学生逆向思维的意识和习惯，帮助学生从仅使用正向思维过渡到同时使用正、逆双向思维，克服长期思维定势导致的思维刻板，从而提高学生的数学思维能力。

如，教师在帮助学生理解方差公式S2=[（x1-）2+（x2-）2+…+（xn-）2]时，可从正向告诉学生，这些字母代表的含义，也可以通过例子逆向帮助学生强化公式的意义，如展示例题：一组数据的方差是S2=[（x1-4）2+（x2-4）2+（x3-4）2…+（x10-4）2]，则这组数据共有多少个？平均数是多少？

三、贯穿对逆向思维解题技巧的训练

逆向思维不是靠教师“教出来”的，是学生在各个教学环节中不断亲身经历、不断锻炼，不断积累而形成的。因此，教师要坚持在初中数学教学中不断渗透逆向思维解题的方法，合理利用练习题，帮助学生积累经验，从而逐步提升学生的逆向思维能力。以下就从三个方面举例说明，利用练习题培养学生的逆向思维解题技巧。

（一）逆用运算律

例1：计算129×（-63）+129×58-10×129-94× 71+79×71。

此题看似复杂，涉及乘法分配律的逆运用，对于初学有理数混合运算的学生有一定难度，教师可引导学生细心观察题目特点，使学生发现此题可通过几次逆用乘法分配律大大简化运算。

解：原式=129×（-63+58-10）+71×（-94+79）（乘法分配律的逆用）

=129×（-15）+71×（-15）

=（129+71）×（-15）（乘法分配律的逆用）

=200×（-15）

=-3000

（二）逆序思考问题

例2：已知方程2x2+（p-2）x+=0的两个根分别为某正方形的内切圆半径和外接圆半径，求p的值。

分析：若按正向思维，应得关于p的方程

但解此方程非常麻烦。如果逆向思考，设正方形内切圆半径为r，则外接圆半径为r，由根与系数的关系得：

（三）从问题的对立面入手

例3，若下列两个方程x2-2（a-1）x+（a2+3）= 0；x2-2ax+a2-2a+4=0至少有一个方程有实数根，求实数的取值范围。此题若从正面着手，则情况较多。相反，如果我们从至少有一个方程有实数根的对立面，即两个方程都没有实数根考虑，则得到以下解法：

解不等式组：

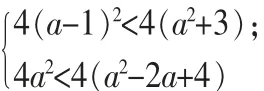
得-1

此题由于采用了逆向思维，解法变得如此简捷。

四、分析法

分析法是一种执果索因的逆向思维过程，指从要证的结论出发，逆向寻求使它成立的条件，直到归结为判定一个显然成立的条件为止，从而证明论点的正确性、合理性的论证方法。运用分析法解决问题，便于学生理清题设与结论之间的复杂关系，通过逆向思维获得解题的思路。

例4：已知如图1，△ABD与△AEC都是等边三角形，求证：BE=DC。

图1

分析：在这道题中，教师可用问答的形式