空间探测中动态运动对双向时间交换测距的影响*



空间探测中动态运动对双向时间交换测距的影响*

张美婷**，陆波，邵庆军

(航天东方红卫星有限公司，北京100094)

摘要：为了提高动态运动条件下双向时间交换测距(TWSTT)的精度，满足航天器间高精度自主测量的需要，在传统相对静止模式的基础上，分析了空间探测中目标间动态运动对双向时间交换测距的影响，针对两种典型的运动场景，分析了相对运动影响测距的机理，推导了动态运动条件下的距离解算公式。分析和仿真结果表明：相比传统静止模式，动态条件下的距离解算增加了目标间的相对速度、运动方向及相对距离等影响因素，如果在距离解算时忽略了上述因素，则将引入相应的测距误差，而且相对运动速度越大、相对距离越远，引入的测距误差越大。

关键词：空间探测；航天器间自主测量；双向时间交换测距；动态运动；测距误差

1引言

双向时间交换(Two-way Satellite Time Transfer,TWSTT)是一种高精度时延测试方法，已经被广泛的用于实现地面的双站时间同步[1-3]。目前,TWSTT能够达到纳秒量级的同步精度水平，在地面时钟为高稳、高精度的情况下，站间同步精度更高[4-5]。由于TWSTT能够实现高精度的时间同步，因此近年来有研究将TWSTT技术应用于空间探测中两个航天器间的自主距离测量[6-8]。但是,由于航天器之间存在相对运动，用于地面站时间同步的传统静态TWSTT方式已不能简单地套用，需要根据航天器间相对运动的特点分析动态运动对TWSTT测距的影响[9-13]。

本文在静态TWSTT测距的基础上，分析了空间探测中航天器动态相对运动对TWSTT测距的影响，重点讨论了两种典型相对运动模式，一是两个目标相向运动，二是两个目标反向运动，推导了不同运动模式对应的距离解算公式。分析结果表明：由于航天器间存在动态运动，如果在距离解算时忽略相关运动参量的影响，则将引入相应的测距误差，而且相对运动速度越大、距离越远，所引入的测距误差越大。

2TWSTT测距的基本原理

TWSTT的基本原理如图1所示[14]。

图1　基于TWSTT的测距原理

A站与B站同时向对方发送脉冲信号，利用各自本地的时钟测量对方信号到达的时间，然后双站交互测量信息，利用两个测量信息联合解算，得到双站的时差，由于双站距离固定，因此得到的双站间信号传播延时固定。站A在t0时刻发射信号，经过τAB后到达站B，τAB为信号的传播延时，站B的时间落后于站AΔt，即存在时差Δt。在站A发射信号后Δt，站B发射信号，经过τBA到达站A。为了便于理解，上述描述过程中假设收发设备的接收和发射延时可以忽略。如果考虑收发两端的设备延时，则站A的发射延时为τAt，接收延时为τAr，站B的发射延时为τBt，接收延时为τBr，则图1中TA可以表示为下述形式：

TA=Δt+τBA+τAr+τBt。

(1)

忽略收发延时，则可表示为

TA=Δt+τBA。

(2)

同理，站B的时刻TA可以表示为

TB=τAB-Δt。

(3)

假设站A和B相对静止，A与B间的距离不变，因此τAB等于τBA，表示为τ。经计算可以得到

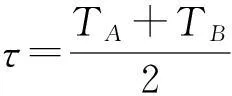
(4)

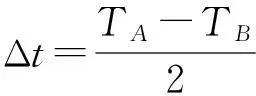
(5)

A与B间的距离可以表示为

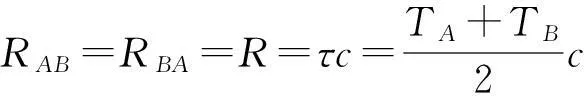
(6)

式中，c表示光速。

如果考虑到收发延时，则式(4)和式(5)可以表示为

(7)

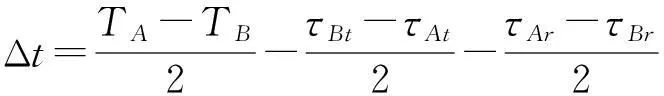
(8)

3动态场景下的TWSTT测距

上节分析以双站静止为前提条件，未考虑双站间的相对运动。本节主要讨论两个航天器相互运动对TWSTT测距带来的影响。

3.1相对接近场景

在这种场景下，两个目标相互运动接近，如图2所示。

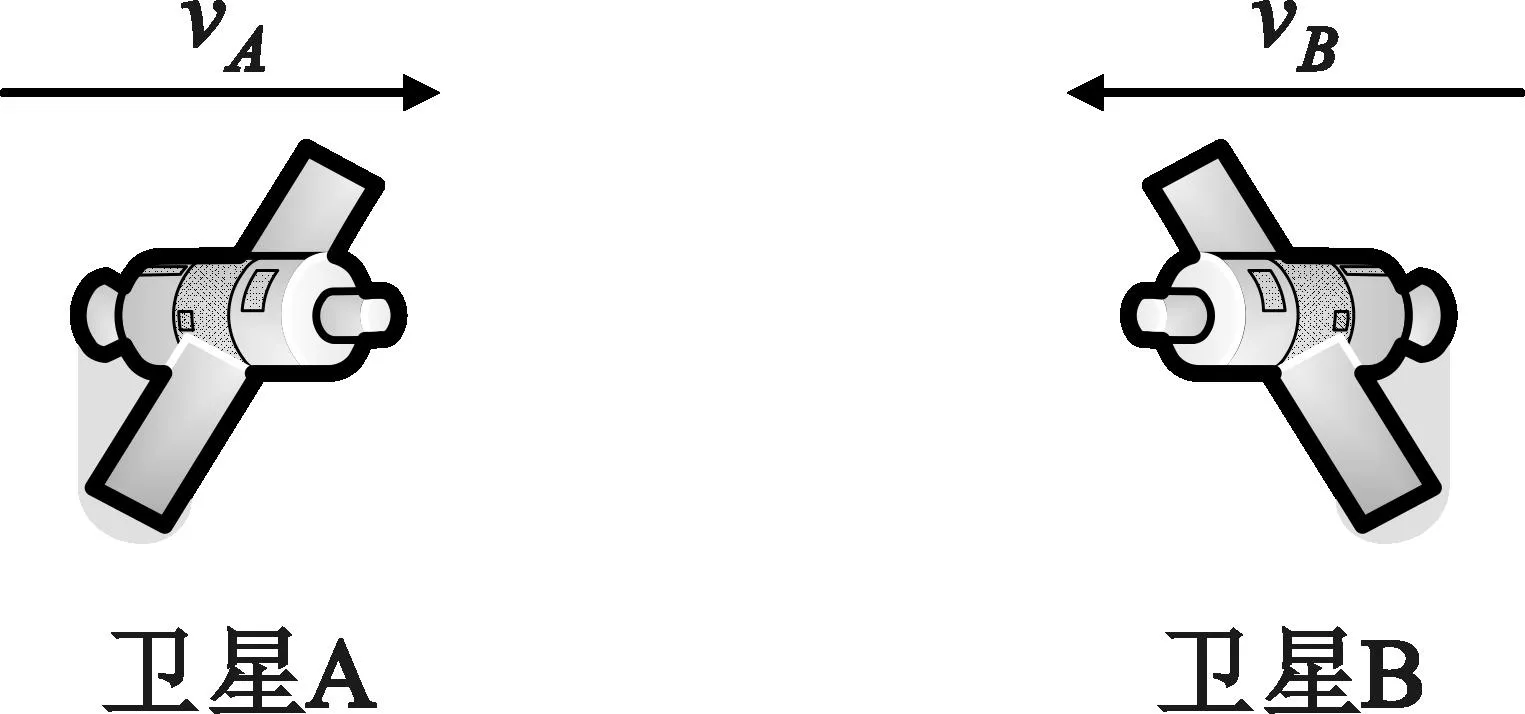
图2　相互接近场景示意图

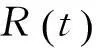
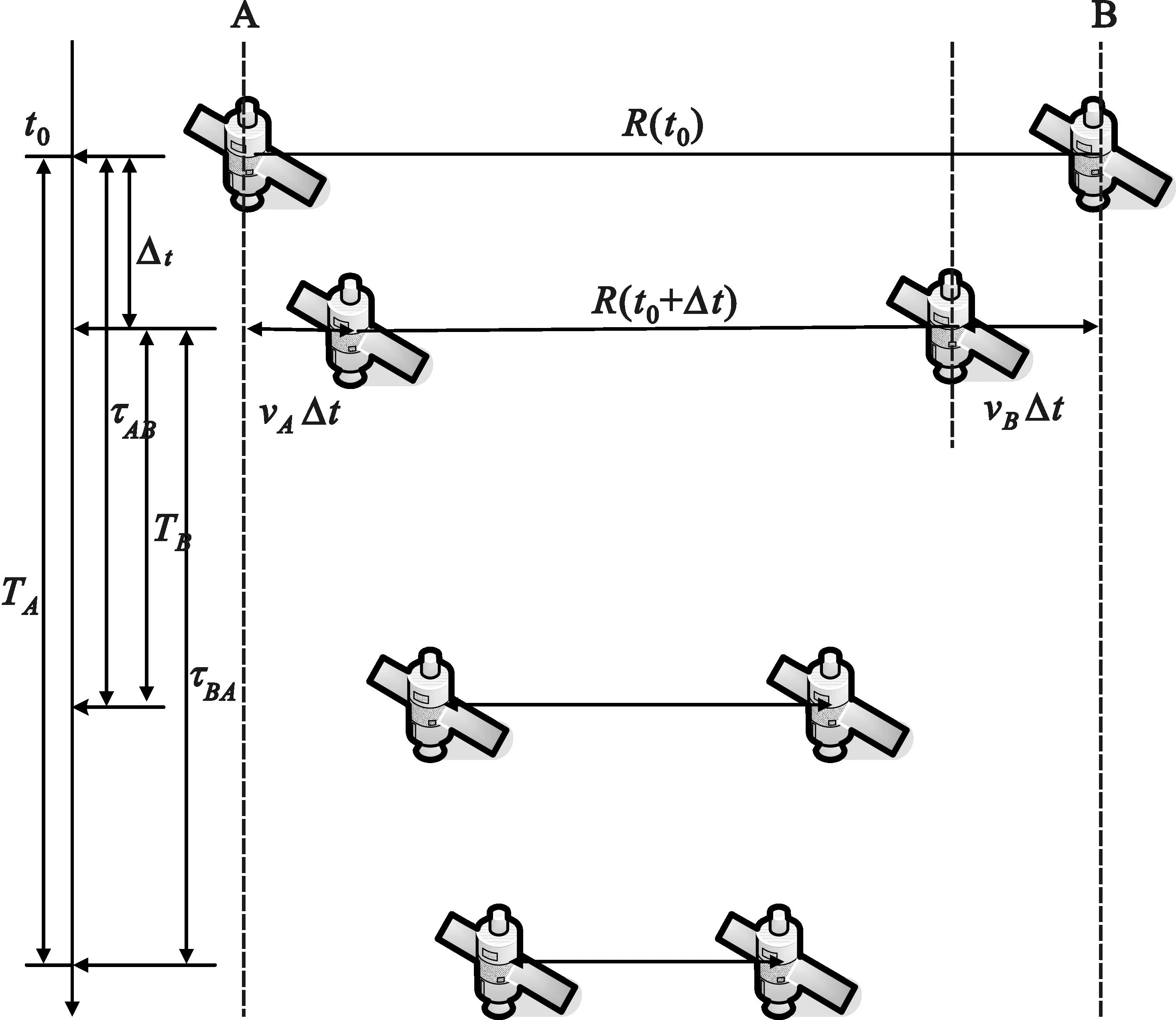
图3　相互接近场景下的测距流程

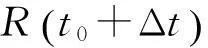
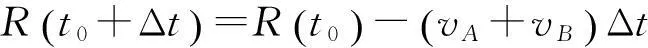
(9)

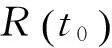
(10)

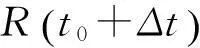
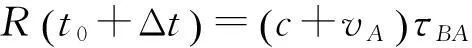
(11)

将式(9)、(10)和(11)合并，可以得到

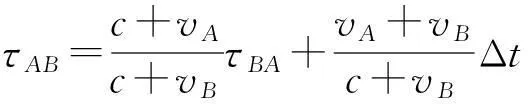
(12)

整理上述公式，可以得到下面结论：

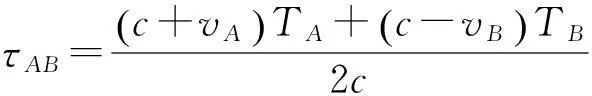
(13)

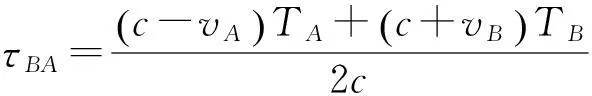
(14)

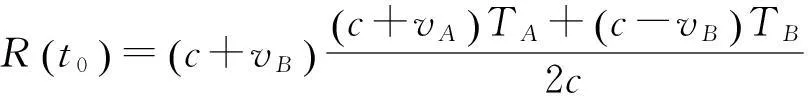
(15)

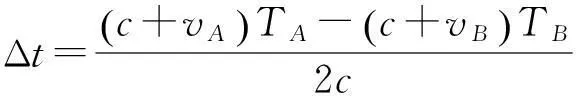
(16)

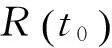
3.2相互远离场景

相互远离场景如图4所示，对应的测量流程如图5所示。

图4　相互远离场景

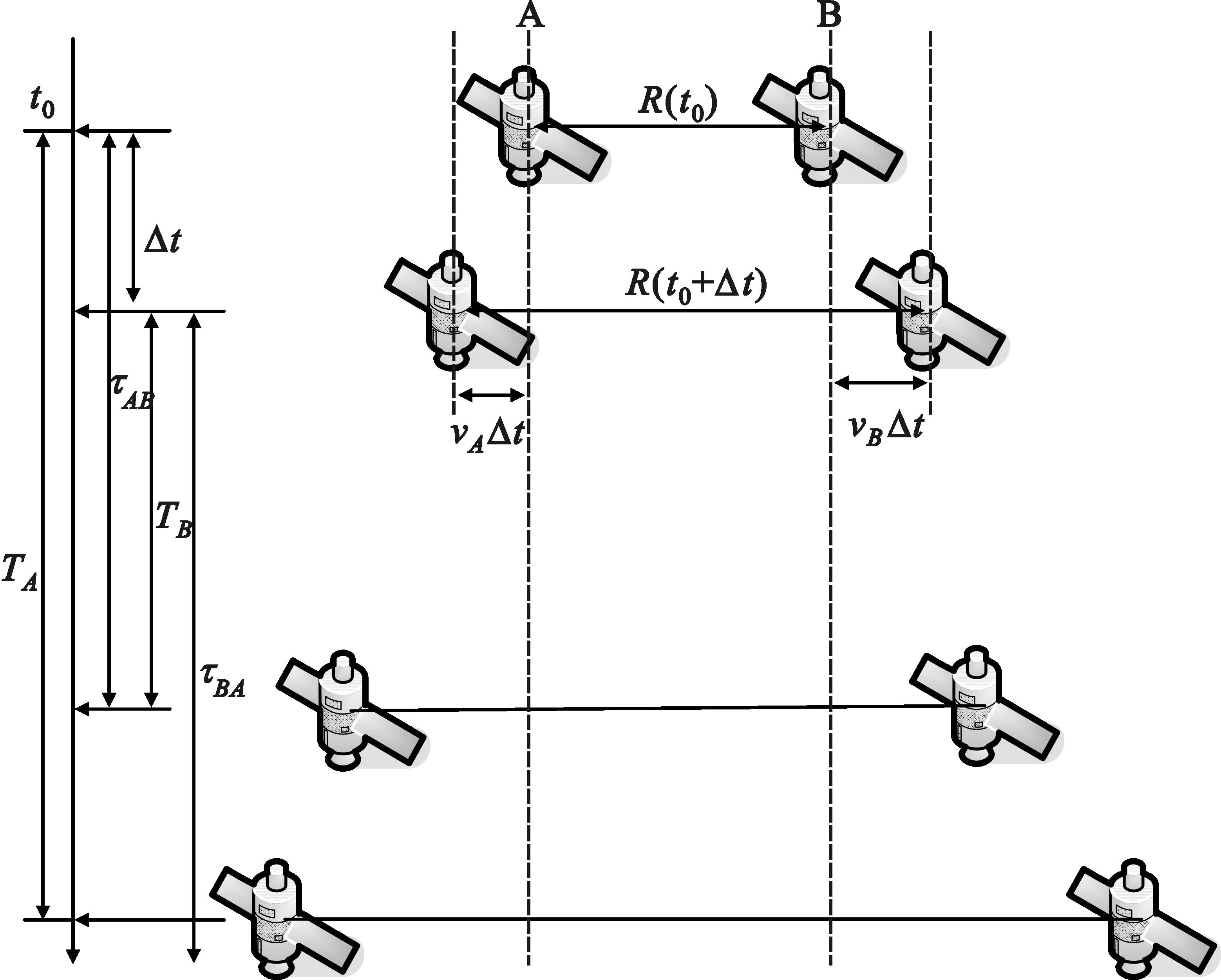
图5　相互接近场景下的测距流程

与图3不同，相互接近运动场景下，目标的距离越来越大，可得到

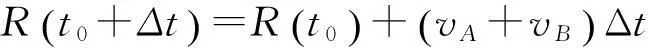
(17)

由此，公式(10)和(11)可以变换为

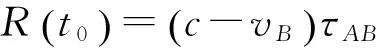
(18)

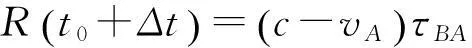
(19)

合并公式(18)、(19)和(17)，可得

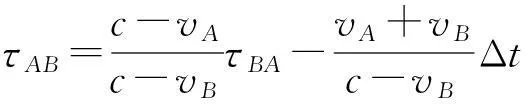
(20)

整理上述公式，可得

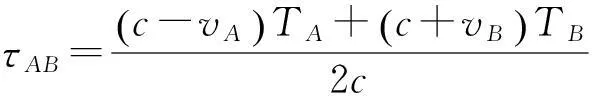
(21)

(22)

(23)

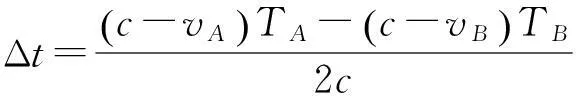
(24)

比较式(15)和式(23)可知，相对运动的方向不同，所得的结果也不同。

4理论分析与仿真

比较式(6)、式(15)和式(23)可知，动态测距方程中增加了航天器运行速度变量v。为了便于理解式(15)，可将其变换为

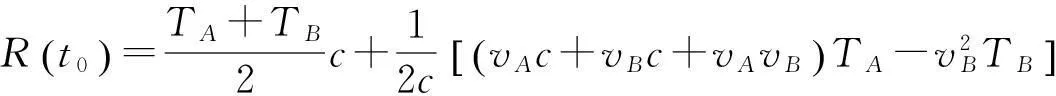
(25)

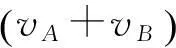
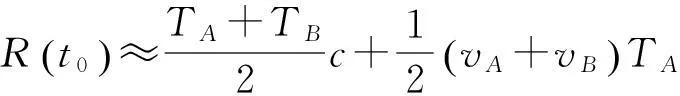
(26)

同理，式(23)可以表示为

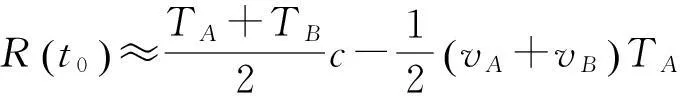
(27)

比较式(26)、式(27)和式(6)可知，相比静止条件下的距离解算公式，在动态运动条件下，目标间的相对运动速度、运动方向以及相对距离和时差成为影响距离解算的新因素。上述分析中均假设以航天器A为初始测量站，航天器A所测量的信号发出和收到时差TA也是造成距离解算误差的主要因素。TA的大小取决于航天器间的相对时钟差和距离，一般情况下时钟差基本固定，那么影响TA大小的主要因素为航天器间的距离。

为了验证上述理论分析的正确性，进一步说明动态运动对航天器自主TWSTT测距的影响，下面选取高、中、低三个轨道高度的航天器，仿真动态运动分别对高轨-中轨和高轨-低轨航天器间自主测量的影响。为了便于分析，本文选取三个类型轨道均为圆轨道，且位于同一轨道面，仅半长轴不同，其他参数均相同，主要轨道参数见表1。

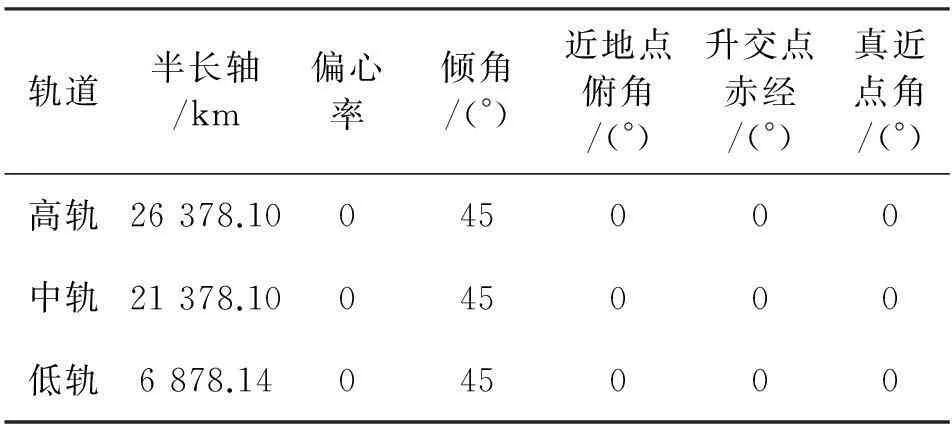
表1　仿真环境中各航天器的轨道参数

根据表1参数配置仿真环境，为了便于说明问题，本文选取0~1000 s飞行弧段的数据为基础进行分析，以50 s为间隔选取测量点，得到的航天器间距离和相对速度分别见图6和图7。

图6　航天器间相对距离仿真结果

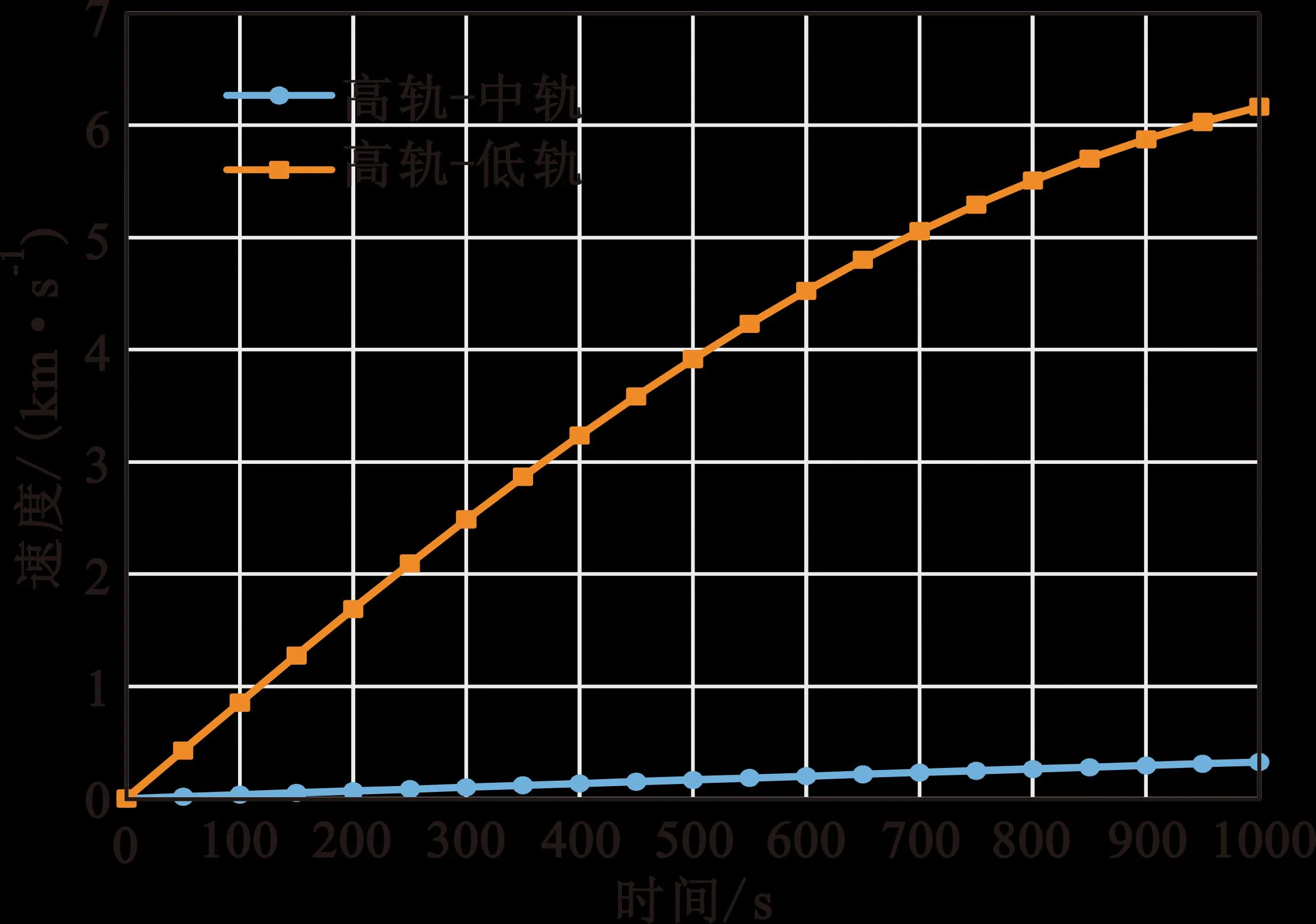
图7　航天器间相对速度仿真结果

从图6和图7可知，高轨-低轨链路相比高轨-中轨链路距离远、相对运动速度高，在这种情况下，如果忽视动态运动对TWSTT测距的影响，则将引入额外的测距误差，如图8所示。

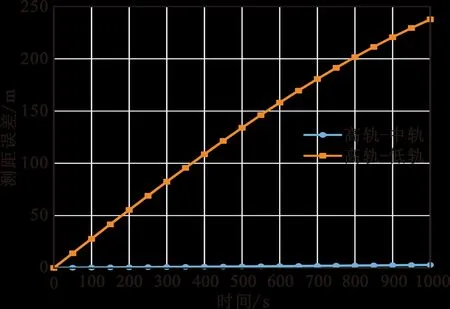
图8　动态运动引入的TWSTT测距误差仿真结果

从图8可知，在动态范围较小时对静态TWSTT测距引入的误差较小，随着航天器间相对距离与速度的增大，引入的测距误差逐渐增大。可见，该误差与航天器间相对速度和相对距离成正比。

5结束语

TWSTT测距技术近年来被逐渐用于航天器间自主测量领域，对大型星座构型、星间测量技术的发展有着重要的意义。传统静态条件下的TWSTT距离解算方法不能满足航天器动态运动条件下测距的需要，简单套用将引入额外的测距误差，影响定位和定轨精度。为此，本文在静态测距的基础上，分析了航天器间动态运动对TWSTT测距的影响，推导了对应的测距解算公式。分析和仿真结果表明：相比静态模式，航天器间的相对运动速度、运动方向及相对距离和时差均为影响动态TWSTT测距的因素；在航天器自主测量过程中，随着相对运动速度和距离的增大，如果忽略上述因素的影响，则导致的测距误差逐渐增大。本文的分析结论对大动态、远距离、高精度条件下TWSTT测距技术的工程应用具有重要的借鉴意义，后面将结合该技术的工程化开展进一步研究。

参考文献：

[1]Kirchner D. Two-way time transfer via communicationsatellites[J]. Proceedings of the IEEE,1991,79(7):983-990.

[2]Hackman C,Jefferts S R,Parker T E. Common-clock two-way satellite time transfer experiments[C]//Proceedings of the 1995 IEEE Internationa Frequency Control Symposium.San Francisco,CA:IEEE,1995:275-281.

[3]Imae M,Hosokawa M,Imamura K,et al. Two-way satellite time and frequency transfer networks in Pacific Rim region[J]. IEEE Transactions on Instrumentation and Measurement,2001,50(2):559-562.

[4]张玲. 卫星双向时间比对法的数字基带设计[J]. 电讯技术,2009,49(10):83-87.

ZHANG Ling. Digital Base-band Design of Two-Way Satellite Time Transfer Device[J]. Telecommunication Engineering,2009,49(10):83-87.(in Chinese)

[5]王学运,张升康. 用于卫星双向时间传递系统的调制器设计[J]. 电讯技术,2012,52(3):400-403.

WANG Xueyun,ZHANG Shengkang. Design of a Modulator for Two-way Satellite Time Transfer(TWSTT) System[J]. Telecommunication Engineering,2012,52(3):400-403.(in Chinese)

[6]黄飞江,卢晓春,刘光灿,等. 星地动态双向时间同步与测距算法[J]. 宇航学报,2014,35(9):1050-1057.

HUANG Feijiang,LU Xiaochun,LIU Guangcan,et al. An Algorithm for Dynamic Satellite-Ground Two-Way Time Synchronization and Ranging[J]. Journal of Astronautics,2014,35(9):1050-1057.(in Chinese)

[7]高有涛,徐波,熊欢欢. 一种提高导航卫星星座自主定轨精度的方法研究[J]. 宇航学报,2014,35(10):65-75.

GAO Youtao,XU Bo,XIONG Huanhuan. A Method for Improving Accuracy of Autonomous Orbit Determination for Navigation Constellation[J]. Journal of Astronautics,2014,35(10) :65-75.(in Chinese)

[8]Huang Feijiang,Lu Xiaochun,Wu Haitao,et al. Algorithm of intersatellite dynamic two-way time transfer based on GEO satellite[C]//Proceedings of Joint Meeting of European Frequency and Time Forum/IEEE International Frequency Control Symposium.Besancon:IEEE,2009:688-691.

[9]Hongwei S,Imae M,Gotoh T. Impact of satellite motion on two-way satellite time and frequency transfer[J]. Electronics Letters,2003,39(5):482-483.

[10]Wu Wenjun,Li Zhigang,Yang Xuhai,et al. A new method for satellite motion correction in TWSTFT[C]// Proceedings of 2012 IEEE International Frequency Control Symposium.Baltimore,MD:IEEE,2012:1 - 4.

[11]Parker T E,Zhang V. Sources of instabilities in two-way satellite time transfer[C]// Proceedings of 2005 IEEE International Frequency Control Symposium and Exposition.Vancouver,BC:IEEE,2005:745-751.

[12]Hongwei S,Imae M. Improvement of precision on two-way satellite time and frequency transfer[J].Electronics Letters,2009,45(18):945-946.

[13]Tseng W,Feng K,Lin S,et al. Sagnac Effect and Diurnal Correction on Two-Way Satellite Time Transfer[J]. IEEE Transactions on Instrumentation and Measurement,2011,60(7):2298 - 2303.

[14]舒炳江. 高精度双向时间比对同步技术原理与应用[J]. 电讯技术,2009,49(1):63-66.

SHU Bingjiang. Theory and Application of Two-way Time Transfer Synchronization Technology[J]. Telecommunication Engineering,2009,49(1) :63-66.(in Chinese)

张美婷(1981—)，女，陕西富平人，2004年获学士学位，现为航天东方红卫星有限公司工程师、北京航空航天大学硕士研究生，主要从事星间链路和无线高速数据传输等方面的研究工作；

ZHANG Meiting was born in Fuping,Shaanxi Province,in 1981. She received the B.S. degree in 2004. She is now an engineer and also a graduate student. Her research concerns technology of inter-satellite links and wireless high speed data transmission,etc.

Email：zh.meiting@gmail.com

陆波(1977—)，男，安徽蚌埠人，2013年获硕士学位，现为航天东方红卫星有限公司工程师，主要研究方向为卫星星间链路技术；

LU Bo was born in Bengbu,Anhui Province,in 1977. He received the M.S. degree in 2013. He is now an engineer. His research concerns the inter-satellite links technology.

邵庆军(1968—)，男，湖北京山人，1994年获学士学位，现为航天东方红卫星有限公司高级工程师，主要研究方向为航天器总体设计。

SHAO Qingjun was born in Jingshan,Hubei Province,in 1968. He received the B.S. degree in 1994.He is now a senior engineer. His research concerns system design of spacecraft.

引用格式：张美婷，陆波，邵庆军.空间探测中动态运动对双向时间交换测距的影响[J].电讯技术，2015,55(4):430-434.[ZHANG Meiting,LU Bo,SHAO Qingjun.Impact of Dynamic Motion on TWSTT Ranging Performance in Space Exploration[J].Telecommunication Engineering,2015,55(4):430-434.]

Impact of Dynamic Motion on TWSTT Ranging

Performance in Space Exploration

ZHANG Meiting,LU Bo,SHAO Qingjun

(DFH Satellite Co.，Ltd.,Beijing 100094,China)

Abstract：To improve the accuracy of two-way satellite time transfer(TWSTT) ranging in dynamic motion scenarios and satisfy the requirement of inter-spacecrafts′ automatic measurement,the impact of dynamic motion on the performance of TWSTT ranging is discussed according to the static ranging principle.For two typical dynamic motion scenarios,the principle of the dynamic motion impacting on the TWSTT ranging is analyzed,and the corresponding ranging equations are deduced. The analysis and simulation results show that compared with the relative static scenario,the velocity and direction of the motion and the distance between the objects must be considered in the dynamic TWSTT ranging calculation. If above parameters are ignored,the calculation error will be involved,and it would become larger with the increasing of velocity and distance.

Key words：space exploration;inter-spacecraft ranging measurement;two-way satellite time transfer(TWSTT) ranging；dynamic motion;ranging error

作者简介：

中图分类号：TN911；P228.1

文献标志码：A

文章编号：1001-893X(2015)04-0430-05

收稿日期：*2014-11-04；修回日期：2015-01-26Received date:2014-11-04；Revised date：2015-01-26

通讯作者：**zh.meiting@gmail.comCorresponding author：zh.meiting@gmail.com